某洞库开挖施工方案模拟

陈 庆 马志明 刘 杰

(1.陆军勤务学院军事设施系，重庆 401311；2.重庆市教育委员会，重庆 400020； 3.西宁联勤保障中心成都房管局昆明房管处，云南 昆明 650000)

某洞库开挖施工方案模拟

陈 庆1,2马志明1刘 杰3

(1.陆军勤务学院军事设施系，重庆 401311；2.重庆市教育委员会，重庆 400020； 3.西宁联勤保障中心成都房管局昆明房管处，云南 昆明 650000)

通过MIDAS对某洞库开挖过程中的竖向位移、塑性区以及等效应力进行了分析，并且对特征点处的模拟数据与实测数据进行了对比，得到有限元分析计算能有效模拟洞库的开挖过程，但由于围岩状态的复杂性，实际工程中不能完全依赖有限元计算方法。

MIDAS,洞库,围岩

1 工程概况

某洞库为14 m跨地下机库，洞库埋深40 m，修建于软质石灰地层，上部为第四纪地层，属于松散堆积物，形成时间较短，地层松软。下部为碎屑岩地层，属于岩石机械风化后形成的岩石碎屑和矿物碎屑，经搬运、沉积、压实、胶结而成的岩石，底层密实。隧洞穿越岩为Ⅲ类，局部破碎带为Ⅳ类。地形起伏，山体肥厚，阶地地势较为平坦。为解决该工程施工方案问题，本章采用数值分析方法进行了方案必选及优化。

2 模型建立

2.1模型范围的确定

要确定模型的计算边界，不仅要满足精度要求，也要节省时间与成本，实践证明：对于洞库开挖所造成的应力、应变影响，仅在洞室周围距洞室中心点3倍～5倍开挖宽度(或高度)的范围内实际存在影响，在3倍宽度处应力变化一般在10%以下，在5倍宽度处应力变化一般在3%以下，此外根据对称性特点，分析区域可以取断面的1/2或1/4。

2.2结构的离散化

将围岩与支护结构离散为仅在节点处铰接的单元体组合时有限单元法的基础。通常情况下，二三节点的杆单元用来模拟锚杆，二三节点的梁单元用以模拟喷射混凝土，三节点与六节点的常应变单元与四节点八节点的等参单元用以模拟围岩与二次衬砌[1]。

将结构体系离散化时应注意：

1)单元各边长不能相差太大，两边夹角不能太小。

2)一个单元不能含有两种材料，边界应设置在材料的分界面与开挖的分界线上。

3)荷载突变处、集中荷载作用点、锚杆处端点必须布置节点。

4)当在材料特性方面和几何形状方面都具有对称性时，可利用对称性进行简化计算。

5)单元划分需考虑分期开挖部分与分部开挖部分的分界线。

2.3边界条件及初始应力条件

由于洞库都是在岩体中开挖，所以计算中一般采取内部加载的方式计算，即开挖在洞库周围释放荷载，数值上等于开挖边界上原先的应力并反向作用于开挖边界上。

计算范围一般采取三种方式：第一是假设为力边界条件，由围岩中的初始应力场确定；二是位移边界条件，假设边界点位移为零；第三是给定混合边界条件，节点一个自由度给定位移，另一个自由度给定节点力。上述每一种计算方法都有误差，且计算范围越小误差越大，在接近边界处误差最大，这种现象称为“边界效应”，而且在动力分析中影响更为显著[2-4]。

2.4有限元分析

复合式衬砌模型的假定：1)围岩和混凝土假定为均质、各向同性的黏弹性材料。2)锚喷支护一般有两种处理方法，一种是提高锚喷加固区的围岩参数来模拟锚喷支护作用，另一种是将喷射混凝土层、钢拱架、锚杆模拟为杆单元；二次衬砌因其较厚，采用四边形等参单元或格桁架单元模拟。3)防水层一般采用有厚度的夹层单元进行模拟，其切向刚度为零，径向刚度一般采用弹性常数E、泊松比μ表示。

围岩力学计算参数和锚杆与喷射混凝土的计算参数见表1和表2。

表1 围岩力学计算参数表

表2 锚杆与喷射混凝土(C20)计算参数表

机库的几何模型简化为三心圆，R1=4.5 m，R2=6 m，A1=60°,A2=55°，如图1所示。

本工程采用环形预留核心土法开挖，每个施工步骤掘进1 m，共开挖14次，采用C20混凝土喷射支护，喷射厚度为0.2 m，每个施工步骤使用11个锚杆，长度为4 m，锚杆间隔为1.5 m，有限单元网格的划分及特征点位移如图2所示。

3 数据分析

3.1竖向位移分析

洞库开挖过程中，竖直方向的位移云图如图3所示(从左到右依次为第一、四、七、十、十二、十四开挖段)。

由图3可以看出，开挖过程中洞库底部凸起位移相对较大以及核心土周围位移较大。

3.2开挖塑性区分析

洞库开挖过程中，塑性区分布如图4所示(从左到右依次为第一、三、六、九、十二、十四开挖段)。

由图4可以看出随着洞库的开挖，逐渐出现塑性区，主要集中在洞库两腰及两侧底部，随着支护作用的起效，塑性区又逐渐消失，其中，第十二开挖段的塑性区范围最大，施工过程中应及时采取支护措施，密切关注监测数据，使安全风险下降至最低。

3.3开挖MISES应力分析

洞库开挖过程中，MISES应力分布云图变化如图5所示(从左到右依次为第一、三、六、九、十二、十四开挖段)。

从图5中可以看出洞库开挖过程中围岩应力的变化趋势，与塑性区相对应，应力值较大处主要存在于洞库底部两侧、两腰及核心土周围，对比塑性区分布图，支护应该密切关注这些对安全有影响的关键位置。

3.4特征点位移分析

A,B,C,D四个特征点计算位移如表3所示。

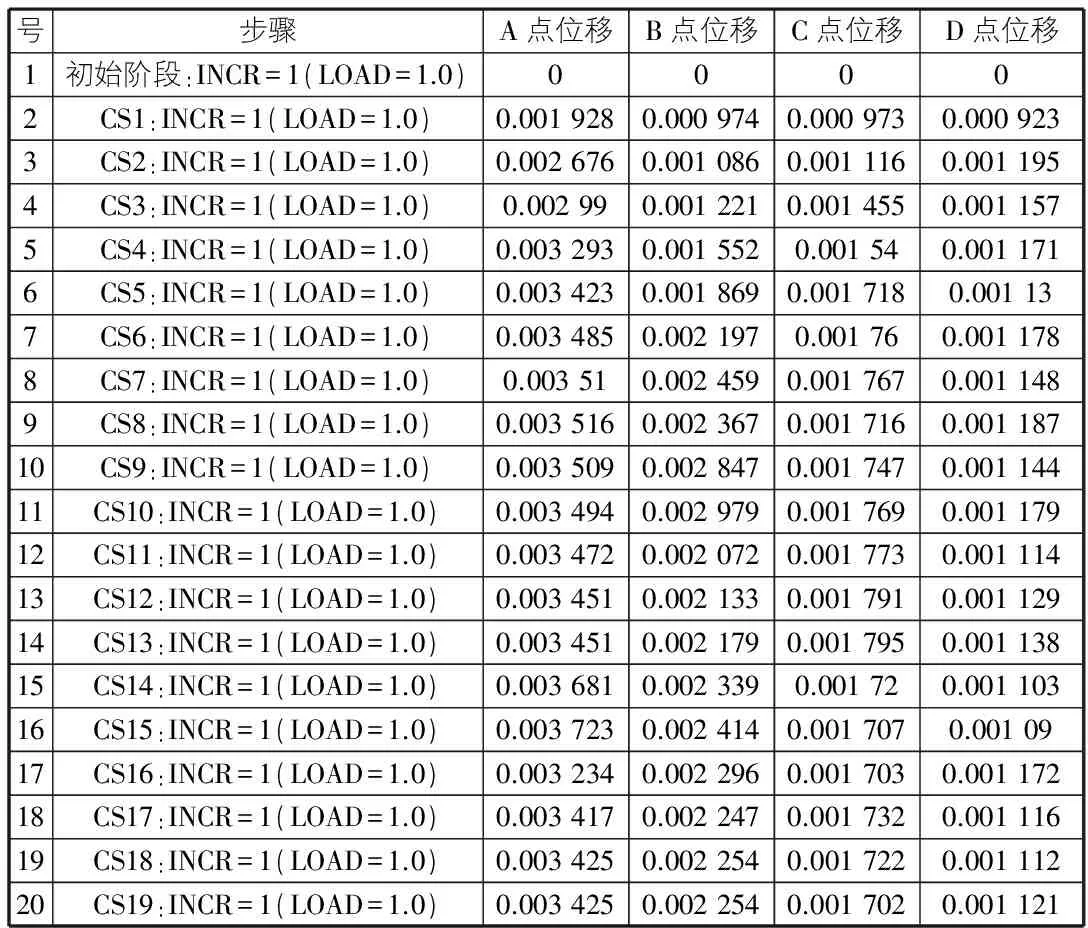
表3 模拟特征点位移表 m

3.5模拟和实测位移分析

最后一个开挖过程数值模拟和实测下沉数据如表4所示。可以看出，除A,B,C三点误差较小外， D点误差达到了24.56%，模拟计算值大于实测位移值，说明开挖后测量仪器还未来得及安装，围岩就已经发生了一部分下沉；另一方面，虽然有限元分析计算作为一种科学、有效的方法能较为准确的预测整个开挖过程中围岩的状态，但由于围岩赋存条件等的复杂性，实际施工过程中，不能完全依赖有限元分析计算。

表4 实测特征点位移表

4 结语

通过MIDAS对某地下机库开挖过程中的竖向位移、塑性区以及等效应力进行了分析，并且对特征点处的模拟数据与实测数据进行了对比，除了极个别数据误差较大以外，绝大部分数据都符合现场量测，证明了有限元分析计算作为一种科学的方法能有效模拟洞库的开挖过程，但由于围岩状态的复杂性，实际工程中不能完全依赖有限元计算方法。

[1] 朱维申，李晓静，郭彦双,等.地下大型洞室群稳定性的系统性研究[J].岩石力学与工程学报，2004，23(10)：1689-1693.

[2] JTG D70—2004,公路隧道设计规范[S].

[3] JTJ 042—94,公路隧道施工技术规范[S].

[4] 况世华.隧道工程技术[M].北京：高等教育出版社,2009:79-81.

Simulationofexcavationconstructionschemeforacave

ChenQing1,2MaZhiming1LiuJie3

(1.DepartmentofMilitaryFacilities,ArmyLogisticsUniversityofPLA,Chongqing401311,China; 2.ChongqingEducationCommittee,Chongqing400020,China；3.KunmingHousingDepartmentofChengduHousingManagementBureauofXiningJointLogisticCenter,Kunming650000,China)

Vertical displacement, plastic zone and equivalent stress for a cave are analyzed by MIDAS in the process of excavation. The simulation method and software are verified on comparing the simulation results with those from experiment of a case. However, due to the complexity state of surrounding rock, the FEM can not be relied on in actual engineering.

MIDAS, cave, surrounding rock

1009-6825(2017)30-0157-03

2017-08-12

陈 庆(1975- )，男，副调研员

TU941

A