基于力约束的空心涡轮叶片陶芯定位方法

崔康， 汪文虎， 蒋睿嵩， 赵德中， 靳淇超

西北工业大学 现代设计与集成制造技术教育部重点实验室， 西安 710072

基于力约束的空心涡轮叶片陶芯定位方法

崔康， 汪文虎， 蒋睿嵩*， 赵德中， 靳淇超

西北工业大学 现代设计与集成制造技术教育部重点实验室， 西安 710072

精铸蜡型作为空心涡轮叶片精铸过程重要的前期工艺转接件，其壁厚精度主要由蜡型模具型腔与内部陶芯的位置匹配关系决定。由于陶芯在模具内完全依靠定位元件实现空间定位，为减小由定位误差引起的陶芯位姿漂移，提出了一种基于力平衡约束的空心涡轮叶片精铸模具陶芯定位布局优化方法。首先，通过建立陶芯定位误差传递模型，揭示了定位误差与陶芯空间位姿扰动量之间的映射关系；其次，根据力平衡原理构建了基于力约束的陶芯定位布局优化模型；之后，针对陶芯表面定位候选点的离散分布特性，结合遗传算法给出了陶芯定位布局点的详细求解策略。最后，仿真对比证明了利用本文所提方法获得的陶芯定位方案可以在保证陶芯定位稳定性的同时提高陶芯定位精度，此外，按照优化后的定位方案压制实际蜡型，壁厚检测结果也进一步表明所提方法的有效性。

空心涡轮叶片； 蜡型； 陶芯； 定位布局； 力平衡； 遗传算法

空心涡轮叶片是航空发动机的核心热端部件，由于结构复杂、精度及强度要求高，目前主要通过熔模精密铸造方法制备，具体流程包括：制芯，模具设计、压蜡、制壳、脱蜡、浇铸等环节。精铸蜡型作为重要前期工艺转接件，其形状精度是影响叶片成形质量的重要因素[1]。空心涡轮叶片精铸蜡型形状精度主要包含外形轮廓精度以及壁厚精度。研究表明：通过提升蜡料性能[2]、预测型面误差[3-5]、优化铸件结构[6]及相关工艺参数[7-8]可以有效改善蜡型外形轮廓精度；而蜡型壁厚精度主要由蜡型模具型腔与内部陶芯的位置匹配关系决定[9]。在蜡型模具中，陶芯完全依靠定位及夹紧元件限位固定，在模具型腔不变的情况下，由定位误差引起的陶芯位姿漂移是导致蜡型壁厚偏差的决定性因素。因此，通过合理设计陶芯定位布局方案，减小定位误差对陶芯定位精度的影响，可以有效提高精铸蜡型壁厚精度。

针对空心涡轮叶片精铸蜡型模具陶芯定位问题，崔康等[10]提出了一种通过逆向调整定位元件尺寸进而提高蜡型壁厚精度的方法。另外，基于模型匹配算法，冯炜等[11]提出了一种陶芯定位元件尺寸计算方法。然而，上述文献并未对陶芯定位布局方案设计展开探讨。事实上，陶芯定位可近似为一般工件定位问题。Asnte[12]基于弹性接触力学相关理论以及有限元仿真技术给出了工件加工过程中各定位夹紧元件载荷计算方法。Wu和Chan[13]以及Chou等[14]以定位夹紧元件载荷为优化目标，分别基于遗传算法和线性规划理论给出了工件定位夹紧布局的相关计算方法。Liao[15]针对板类零件变形量提出了一种板类零件定位夹紧位置空间布局优化方法。Li和Melkote[16]假定工件在加工过程中的弹性位移是由定位夹紧点处的工件弹性变形引起的，并基于此给出了这一种工件定位夹紧布局优化方法。Kaya[17]、Prabhaharan等[18]以及Padmanaban等[19-20]将工件加工过程中表面型值点变形量作为优化目标，分别对呈离散或连续分布状态的定位夹紧候选点集给出了基于有限元理论及启发式算法的定位夹紧布局优化方法。Rex和Ravindran[21]则遍历工件所有可能的定位夹紧方案，通过对加工过程进行数值仿真，得到了最优定位夹紧方案。然而，上述方法均是以减小定位夹紧元件受力或工件变形量为主要优化目标，并未考虑定位误差对工件定位精度的影响。Wang等[22-23]和Xiong等[24]提出一种基于定位误差模型的工件定位布局优化方法，但由于没有考虑工件自重对定位方案的影响，因此，优化结果常无法满足工件定位稳定性要求；此外，由于该模型采用Greed算法和Interchange算法求解，因此，计算结果也常陷入局部最优。

为此，本文针对空心涡轮叶片精铸蜡型模具陶芯定位问题，提出了一种基于力平衡约束的定位布局求解方法。首先通过建立定位误差传递模型，获得了陶芯定位误差与空间位姿扰动量之间的映射关系。其次，考虑到陶芯自重问题，建立了基于力平衡约束的陶芯定位布局优化模型，并结合遗传算法给出了该模型的详细求解步骤。最后，结合具体实例对本文及Wang等[22-23]所提方法进行了对比验证，结果表明本文所提方法在陶芯定位稳定性以及定位误差控制方面具有一定优势，可为空心涡轮叶片蜡型壁厚控制提供基础理论。

1 定位误差传递模型

如图1所示，在空心涡轮叶片蜡型压制过程中，陶芯完全依靠定位及夹紧元件实现空间限位，定位元件决定了陶芯空间姿态，夹紧元件保证了陶芯与定位元件始终接触。由于定位元件存在定位误差，陶芯实际位姿相较于理论位置必然存在一定扰动。为研究定位布局方案对陶芯定位精度的影响，首先需要建立定位误差与陶芯空间位姿扰动量之间的函数关系。

图1 陶芯定位示意图Fig.1 Illustration of ceramic core localization

根据刚体运动学知识可知，刚体在三维空间o-xyz内的任意运动可以分解为沿某方向λ的平移运动及绕某方向ω的旋转运动。假设由定位误差引起的陶芯空间位姿扰动量为

Δq=[ΔbTΔθT]T

(1)

式中:Δb=[ΔbxΔbyΔbz]T为平移扰动量；Δθ=[ΔθxΔθyΔθz]T=Θ·τ为旋转扰动量，且τ为沿旋转轴ω方向的单位向量，Θ为转动角。如图2所示，陶芯表面上任意一点i的位置偏移量Δri也必然包含平移分量Δb以及另外一个绕轴ω的旋转分量Δφi，即

Δri=Δb+Δφi

(2)

此外，由图2可知，当旋转扰动量Δθ较小时，Δφi的表达式为

Δφi≈(Θdi)·ci=Θ·(τ×ri)=Δθ×ri

(3)

式中：di为点i到旋转轴ω的欧式距离；Θdi为旋转弧长；ci为沿旋转方向且与由旋转轴ω及点i所

图2 陶芯定位误差传递模型Fig.2 Model for locating error transfer of ceramic core

构成的平面垂直的单位向量；ri为点i的坐标向量。

由此，联立式(2)和式(3)可以得陶芯空间位姿扰动量Δq与陶芯表面点i位置偏移量Δri之间的映射关系为

Δri=Δb+Δθ×ri

(4)

另外，由于点i坐标ri满足陶芯型面方程：

f(ri)=0

(5)

因此，对式(5)微分可以进一步求得陶芯表面点i处指向陶芯内部的单位法向矢量为

(6)

事实上，若点i恰好是陶芯表面某定位点，且将偏移量Δri在点i法矢方向的投影近似为定位元件在该点处的定位误差，那么，陶芯定位误差与陶芯空间位姿扰动量之间的映射关系可简化为

(7)

式中：ji=[(dri)T(ri×dri)T]T。

当陶芯表面存在k个定位点，且定位误差分别为Δe1、Δe2、Δe3、…、Δek，代入式(7)联立可得定位误差与陶芯空间位姿扰动量之间的函数关系：

(8)

式中：J为定位Jacobian矩阵。

另外，考虑工件定位完整性，当陶芯表面各定位点不存在定位误差：ΔE=0，陶芯的空间位姿应唯一存在，即Δq=0应是式(8)的唯一解。由此可知：陶芯表面至少需要6个定位点，且对应定位Jacobian矩阵J满秩，才能保证陶芯空间位姿唯一不变。

2 定位布局优化模型

根据式(8)可知，陶芯空间位姿扰动量Δq不仅取决于定位误差，同时还与定位Jacobian矩阵J有关，前者是由定位元件制造误差及装配误差造成，不可避免；后者取决于定位点在陶芯表面的空间分布。因此，在保证陶芯定位完整性的前提下，寻求一种最佳定位布局方案使得相同定位误差条件下陶芯位姿扰动量最小是空心涡轮叶片精铸蜡型模具陶芯定位布局设计的主要目标。

2.1 定位布局求解基本模型

对式(8)作如下变换：

ΔE=JΔq⟹

(9)

同时令：

M=JTJ

(10)

综上所述，陶芯定位布局基本求解模型可以表述为：在陶芯表面的候选点集P_set中找出使接触信息矩阵行列式det(M)最大的6个定位点，且该行列式最大值det(M)max≠0，即

(11)

2.2 重力平衡约束条件

陶芯定位元件不仅决定了陶芯的空间位姿，其还应该满足陶芯定位稳定性需求，即在定位点处由陶芯自重引起的定位元件反作用力应与陶芯自重满足静力平衡关系，从而防止陶芯置放时滑移、滑落。

陶芯在蜡型模具中一般采用叶盆朝下或者叶背朝下两种置放形式，如图3所示。将两种置放形式下的陶芯重力载荷分别表示为Gbasin、Gback，且

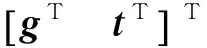
(12)

图3 陶芯定位方式Fig.3 Locating modes of ceramic core

式中：g为叶盆朝下时的重力矢量；t为叶盆朝下时的重力矩矢量。在不考虑陶芯与定位元件之间摩擦力的情况下，上述两种置放形式对应的陶芯定位静力平衡方程可表示为

(13)

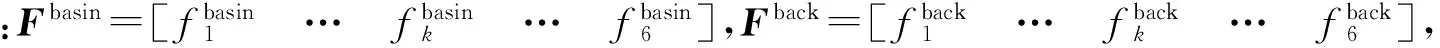
(14)

在陶芯定位过程中，定位元件只能提供沿接触点法矢方向且指向陶芯内部的正压力。针对上述两种置放形式，如果在任意一种置放形式下，若某种陶芯定位布局方案能使得定位点平衡力大于零，即正压力，那么可以认为该定位布局方案满足陶芯定位稳定性需求。因此，基于重力平衡的陶芯定位布局求解约束条件可表示为

(15)

据此，基于重力约束的空心涡轮叶片精铸蜡型模具陶芯定位布局求解问题可以表示为

(16)

为了便于求解，现将式(16)模型作出如下简化：

1) 针对约束条件一，如果优化结果det(M)max=0，那么本次候选点集中不存在满足陶芯定位唯一性的定位布局方案，因此需要更新候选点集。但是在模型优化求解过程中，不需要考虑约束条件一对优化结果的影响。

2) 针对约束条件二，可以采用内部惩罚法，将约束条件整合到优化模型中。最终得到无约束的空心涡轮叶片蜡型模具陶芯定位布局求解模型：

6 points→from:P_set

(17)

式中：γ、η为力平衡约束因子。

3 模型优化算法

由于陶芯表面定位候选点集呈离散分布状态，且候选点与优化模型不存在明显的梯度关系，因此针对连续参数空间的传统优化算法并不适用于上述模型的求解。目前，针对离散空间的模型优化问题，一般采用启发式算法求解。遗传算法就是一种针对非连续参数空间，通过模拟生物进化机制从而实现高效、并行、全局搜索的启发式优化算法。该方法不依赖优化模型的梯度信息，采用概率化的寻优方式，能够跳出局部最优解并自适应的调整搜索方向，非常适合本文所提陶芯定位布局优化模型。因此，本文基于遗传算法，建立了空心涡轮叶片精铸蜡型模具陶芯定位布局优化模型求解方法，具体步骤如下：

步骤1 候选点选择。在陶芯表面适合定位的部位选取N个候选点，对其进行二进制编码。

步骤2 初始化。选取m种布局方案作为初始种群，且m为偶数。每种方案被称之为种群个体，每个种群个体包含了6个从候选点集中随机挑选的定位点。

步骤3 个体评价。按照式(18)对初始种群进行个体评价，计算每个个体的适应度Ti。

i=1,2，…,m

(18)

步骤4 选择运算。按照式(19)计算初值种群每个个体被挑选到的概率分布pi，并利用随机数在初始种群中挑选m/2对个体。

(19)

步骤5 交叉及变异运算。基于每个个体在候选点中的二进制编码，对步骤4中m/2对个体进行交叉及变异置换，并按照式(18)重新对交叉变异后的m个个体的适应度进行求解。

步骤6 种群迭代。在初始种群以及交叉变异后的种群中分别选取适应度最大的2个和m-2个个体作为下次迭代的初始种群，并跳转至步骤3。

步骤7 停止条件。当迭代次数超过预设最高迭代次数n时，计算终止。

4 算法验证

结合具体空心涡轮叶片精铸蜡型模具陶芯定位布局问题，对上述算法及Wang等[22-23]所提算法进行了对比分析，并通过压制实际蜡型对优化结果进行了实例验证，分析及验证过程如下。

4.1 对比计算

图4为验证用空心涡轮叶片精铸蜡型陶芯三维模型。由陶芯定位原理可知，在蜡型压制完成后蜡型表面会残留定位孔，为保证蜡型叶身型面质量，定位元件候选点应分布在叶尖以及叶根位置，同时综合考虑蜡型模具结构及陶芯装夹工艺特点，最终在陶芯表面选取了256个定位候选点，如图5所示。

另外，基于陶芯型面方程，获取了各候选点空间坐标以及指向陶芯内部的单位法向矢量，并将陶芯定位布局优化模型及求解算法中的相关参数设置如表1所示。

图4 实验用陶芯三维模型Fig.4 3D model of experimental ceramic core

最后，利用遗传算法对目标方程式(17)进行了迭代求解，结果表明每代种群的个体适应度最大值Tmax呈收敛状态，如图6所示。最终得到的陶芯定位布局方案如图7所示。图8为基于Wang等[22-23]所提方法求解得到的陶芯定位布局方案。

为验证上述方案是否满足陶芯定位稳定性要求，根据式(14)分别计算了两种方案下为平衡陶芯重力各定位点所需力的大小，结果如表2所示。

图5 陶芯定位候选点Fig.5 Locating candidate points of experimental ceramic core

表1 陶芯定位布局优化模型相关参数值

Table 1 Parameter values involved in optimization model for layout of ceramic core localization

ParameterγηmnValue11100500

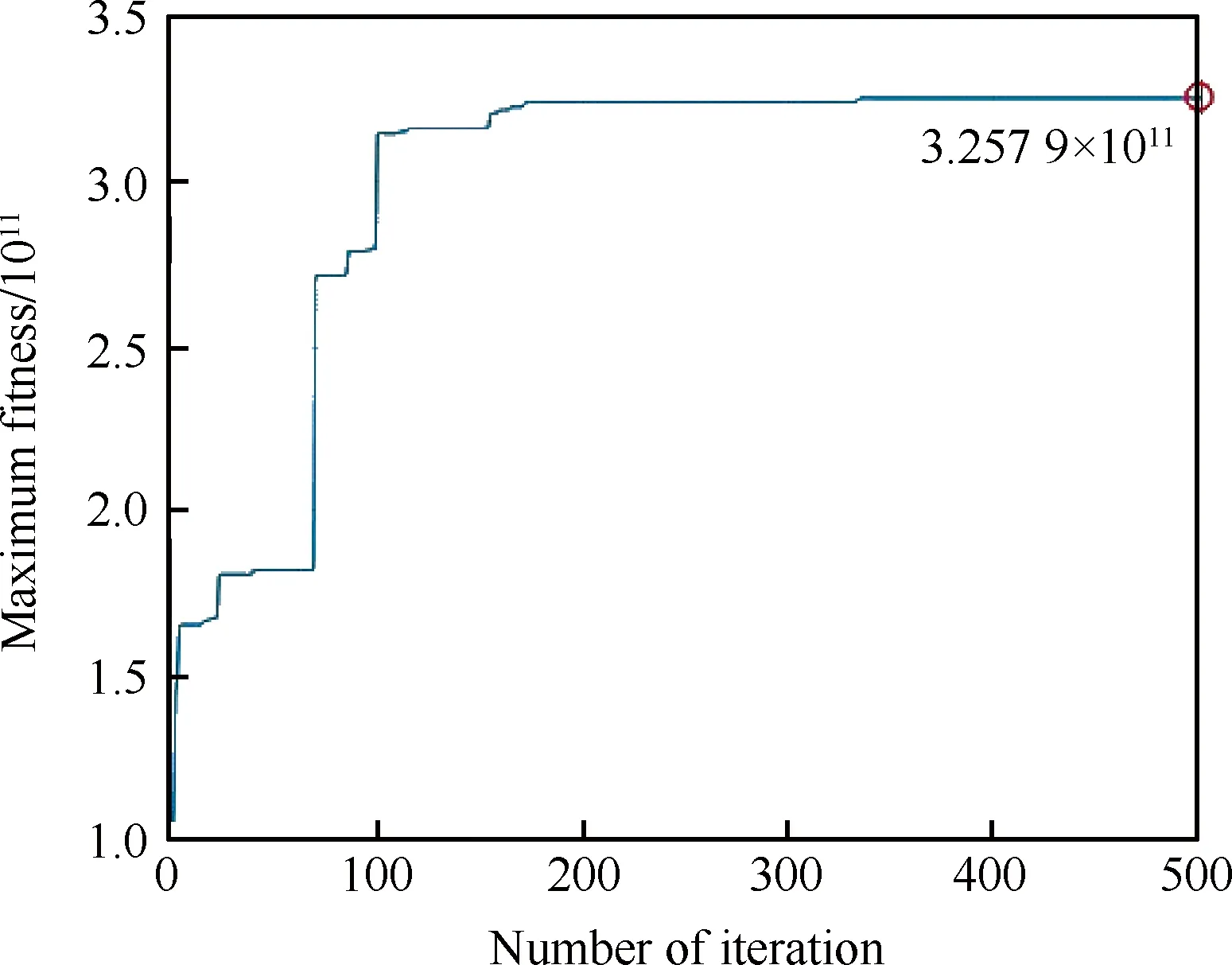
图6 各代种群适应度最大值Fig.6 Maximum individual fitness in each generation

图7 陶芯定位方案1Fig.7 Locating strategy 1

图8 陶芯定位方案2Fig.8 Locating strategy 2

表2 两种定位方案各定位元件陶芯重力反作用力大小Table 2 Reacting forces required from locating rods to balance core gravity with respect to two locating strategies

LocatingstrategyForcerequiredfromlocation/NRod1Rod2Rod3Rod4Rod5Rod6100.00150.6398 0.01670.2929 0.5507200.18620.7117-0.04930.8375-0.0237

在方案1中，各定位点所需要提供的力均大于0，即：所有定位元件只需提供正压力便可满足陶芯静力平衡。相反，在方案2中，定位元件需要在定位点4、6处提供拉力，明显不满足陶芯定位稳定性需求。由此可见，本文所提算法能够有效约束定位元件布局方案使其满足陶芯静力平衡需求。优化后的方案可以在置放陶芯时为陶芯提供足够支撑，防止其滑移或滑落。

另外，为验证本文所提方法在陶芯定位误差控制方面的性能，本文设计如下对比实验：

步骤1 由于陶芯定位误差具有统计意义，即各个定位点误差均服从独立的正态分布。为此，基于正态分布N(0,0.05)为上述两种定位方案分别随机生成了1 000组定位误差。

步骤2 根据式(8)分别计算每组定位误差引起的陶芯空间位姿扰动量Δq。

步骤3 陶芯空间位姿扰动量包含平移扰动量以及旋转扰动量，由于平移和旋转具有累加效应，因此无法直观的通过位姿扰动量对陶芯位姿变化进行判定。为此在陶芯表面对蜡型壁厚影响最为敏感前后缘位置挑选了100个评估点(如图9 所示)，分别计算陶芯漂移前后位姿评估点的空间位移量，并将最大值作为陶芯位姿变化的衡量标准。

计算结果如图10和图11所示。在定位方案1中，1 000组定位误差引起的陶芯位姿评估点最大

图9 陶芯漂移评估点Fig.9 Evaluating points for shift of ceramic core

图10 基于定位方案1的陶芯最大偏移量 Fig.10 Maximum displacement of ceramic core with respect to locating strategy 1

图11 基于定位方案2的陶芯最大偏移量 Fig.11 Maximum displacement of ceramic core with respect to locating strategy 2

位移量的平均值为0.068 7 mm。在定位方案2中，该值为0.086 3 mm。上述结果说明，相较于Wang等[22-23]的方法，本文所提算法在保证陶芯定位稳定性的同时在陶芯定位误差控制方面也具有一定优越性。

4.2 实例验证

按照图7所示的陶芯定位布局方案及陶芯置放形式(叶盆朝下)，作者设计了相应的定位元件以及蜡型模具，如图12所示。最终，基于表3所示的工艺参数压制了实际蜡型5组，如图13所示。对关键截面进行壁厚测量，结果表明蜡型壁厚满足设计公差需求(±0.05 mm)，如表4所示。该实验证明了本文所提方法具有一定实际可行性。

图12 蜡型模具及压蜡过程Fig.12 Wax pattern die and wax injection process

表3 压蜡工艺参数Table 3 Parameter values of wax injection experiment

ParameterInjectionpressure/MPaHoldingpressure/MPaWaxtempera-ture/℃Holdingtime/sCoolingtime/sValue1.01.0602020

图13 精铸蜡型Fig.13 Wax patterns

表4 精铸蜡型测量截面最大壁厚偏差

Table 4 Maximum wall-thickness errors for measurement sections of wax patterns

Numberofmea-surementsectionError/mmPattern1Pattern2Pattern3Pattern4Pattern51 0.048 0.039-0.026 0.039-0.0312-0.036-0.041 0.037-0.048 0.0383 0.042 0.047 0.046-0.041-0.039

5 结 论

1) 基于刚体定位误差传递理论以及静力平衡原理，提出了一种空心涡轮叶片精铸蜡型模具陶芯定位布局优化模型，并结合遗传算法给出了该模型的求解方法。

2) 仿真对比分析发现：相较于Wang等[22-23]所提的方法，利用本文所提方法得到的陶芯定位布局方案可以在保证陶芯定位力学稳定性的同时进一步减小由陶芯定位误差引起的陶芯位姿漂移。

3) 压蜡实验表明：利用本文所提方法设计的陶芯定位方案可以保证压制出的蜡型壁厚精度满足设计公差要求(小于±0.05 mm)。

4) 值得指出的是：压蜡工艺参数对蜡型壁厚精度也会产生一定影响，而本文未就工艺参数的选择及优化展开讨论，该方面的研究将在后续论文中进行深入探讨。

[1] PETES F, VOIGT R, BLAIR M. Dimensional repeatability of investment castings[C]//9th World Conference on Investment Casting. Montvale, NJ: Investment Casting Institute, 1996: 22.

[2] BEMBLAGE O, KARUNAKAR D B. A Study on the blended wax patterns in investment casting process[C]//Proceedings of the World Congress on engineering. The International Association of Engineers, 2011, 1: 6-8.

[3] SINGH B, KUMAR P, MISHRA B K. Simulation of wax pattern dimensions for accuracy improvement in ceramic shell investment casting[J]. International Journal of Surface Engineering & Materials Technology, 2013, 3(1): 45-50.

[4] SABAU A S, VISWANATHAN S. Prediction of wax pattern dimensions in investment casting[J]. Transactions-American Foundrymens Society, 2002, 1: 733-746.

[5] SABAU A S, VISWANATHAN S. Material properties for predicting wax pattern dimensions in investment casting[J]. Materials Science and Engineering: A, 2003, 362(1): 125-134.

[6] LIU C, JIN S, LAI X, et al. Influence of complex structure on the shrinkage of part in investment casting process[J]. The International Journal of Advanced Manufacturing Technology, 2015, 77(5-8): 1191-1203.

[7] SINGH B, KUMAR P, MISHRA B K. Simulation of wax pattern dimensions for accuracy improvement in ceramic shell investment casting[J]. International Journal of Surface Engineering and Materials Technology, 2013, 3(1): 45-50.

[8] PATTNAIK S, KARUNAKAR D B, JHA P K. Multi-characteristic optimization of wax patterns in the investment casting process using grey-fuzzy logic[J]. The International Journal of Advanced Manufacturing Technology, 2013, 67(5-8): 1577-1587.

[9] JIANG R S, WANG W H, ZHANG D H, et al. Wall thickness monitoring method for wax pattern of hollow turbine blade[J]. The International Journal of Advanced Manufacturing Technology, 2016, 83(5): 949-960.

[10] 崔康, 汪文虎, 蒋睿嵩, 等. 涡轮叶片精铸模具陶芯定位元件逆向调整算法[J]. 航空学报, 2011, 32(10): 1924-1929.

CUI K, WANG W H, JIANG R S, et al. Reverse adjustment algorithm of ceramic core locators in hollow turbine blade investment casting die[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(10): 1924-1929 (in Chinese).

[11] 冯炜, 汪文虎, 王孝忠, 等. 空心涡轮叶片精铸蜡型陶芯定位元件尺寸计算方法[J]. 航空学报, 2013, 34(1): 181-186.

FENG W, WANG W H, WANG X Z, et al. Size calculation method of ceramic core locators for hollow turbine blade investment casting wax pattern[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(1): 181-186 (in Chinese).

[12] ASNTE J N. A combined contact elasticity and finite element-based model for contact load and pressure distribution calculation in a frictional workpiece-fixture system[J]. The International Journal of Advanced Manufacturing Technology, 2008, 39(5-6): 578-588.

[13] WU N H, CHAN K C. A genetic algorithm based approach to optimal fixture configuration[J]. Computers & Industrial Engineering, 1996, 31(3): 919-924.

[14] CHOU Y C, CHANDRU V, BARASH M M. A mathematical approach to automatic configuration of machining fixtures: analysis and synthesis[J]. Journal of Engineering for Industry, 1989, 111(4): 299-306.

[15] LIAO Y G. A genetic algorithm-based fixture locating positions and clamping schemes optimization[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2003, 217(8): 1075-1083.

[16] LI B, MELKOTE S N. Improved workpiece location accuracy through fixture layout optimization[J]. International Journal of Machine Tools and Manufacture, 1999, 39(6): 871-883.

[17] KAYA N. Machining fixture locating and clamping position optimization using genetic algorithms[J]. Computers in Industry, 2006, 57(2): 112-120.

[18] PRABHAHARAN G, PADMANABAN K P, KRISHNAKUMAR R. Machining fixture layout optimization using FEM and evolutionary techniques[J]. The International Journal of Advanced Manufacturing Technology, 2007, 32(11-12): 1090-1103.

[19] PADMANABAN K P, PRABHAHARAN G. Dynamic analysis on optimal placement of fixturing elements using evolutionary techniques[J]. International Journal of Production Research, 2008, 46(15): 4177-4214.

[20] PADMANABAN K P, ARULSHRI K P, PRABHAHARAN G. Machining fixture layout design using ant colony algorithm based continuous optimization method[J]. The International Journal of Advanced Manufacturing Technology, 2009, 45(9-10): 922-934.

[21] REX F M T, RAVINDRAN D. An integrated approach for optimal fixture layout design[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2017， 231(7)： 1217-1228.

[22] WANG M Y, PELINESCU D M. Optimizing fixture layout in a point-set domain[J]. IEEE Transactions on Robotics and Automation, 2001, 17(3): 312-323.

[23] WANG M Y. An optimum design for 3-D fixture synthesis in a point set domain[J]. IEEE Transactions on Robotics and Automation, 2000, 16(6): 839-846.

[24] XIONG Z, WANG M Y, LI Z. A near-optimal probing strategy for workpiece localization[J]. IEEE Transactions on Robotics, 2004, 20(4): 668-676.

[25] ATKINSON A C, DONEV A N, TOBIAS R D. Optimum experimental designs, with SAS[M]. Oxford: Oxford University Press, 2007: 137-147.

(责任编辑： 李世秋)

*Corresponding author. E-mail: jiangrs@nwpu.edu.cn

Force-constraint method for localization of ceramic core of hollow turbine blade

CUI Kang, WANG Wenhu, JIANG Ruisong*, ZHAO Dezhong, JIN Qichao

KeyLaboratoryofContemporaryDesignandIntegratedManufacturingTechnologyofMinistryofEducation,NorthwesternPolytechnicalUniversity,Xi’an710072,China

The wax pattern is always used as a dimension transfer component in near-net-shape casting process for a hollow turbine blade, and its wall-thickness accuracy entirely depends on the positional relationship between the die cavity of the wax pattern and the internal ceramic core. Generally, the ceramic core is located in the wax pattern die through a series of locating rods. In order to reduce the positional shift of the ceramic core caused by locating errors, a locating layout optimization method based on the force-balance constraint is proposed in this paper. An error transfer model, which formulates the mapping relationship between localization errors and perpetuation of the ceramic core, is established. According to the static equilibrium theory, an optimization model for locating the layout of the ceramic core is then proposed based on gravity constraint. Considering the discrete feature of locating the candidate point on the surface of the ceramic core, a solving strategy for the optimization model is given by utilizing the genetic algorithm. Comparisons of simulation results prove that the locating layout optimized with the method in this paper can improve the localization accuracy of the ceramic core, while guaranteeing the localization stability. Based on a wax injection experiment, the feasibility of the optimization result is also demonstrated.

hollow turbine blade; wax pattern; ceramic core; localization layout; force balance; genetic algorithm

2017-03-01； Revised： 2017-04-13； Accepted： 2017-04-21； Published online： 2017-05-19 09:27

URL： www.cnki.net/kcms/detail/11.1929.V.20170519.0927.004.html

s： National Natural Science Foundation of China (51475374, 51505387)； the Fundamental Research Funds for the Central Universities (3102015ZY087)

V263.1

A

1000-6893(2017)09-421209-09

2017-03-01； 退修日期： 2017-04-13； 录用日期： 2017-04-21； 网络出版时间： 2017-05-19 09:27

www.cnki.net/kcms/detail/11.1929.V.20170519.0927.004.html

国家自然科学基金(51475374, 51505387)； 中央高校基本科研业务费专项资金(3102015ZY087)

*通讯作者.E-mail: jiangrs@nwpu.edu.cn

崔康， 汪文虎， 蒋睿嵩， 等． 基于力约束的空心涡轮叶片陶芯定位方法[J]． 航空学报, 2017, 38(9): 421209. CUI K, WANG W H, JIANG R S, et al. Force-constraint method for localization of ceramic core of hollow turbine blade[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(9): 421209.

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2017.421209