分子模拟数据可视化的MATLAB实现

李健++冯剑

摘要：将分子模拟数据可视化是重要的形象化描述方法。该文利用MATLAB强大的图形处理能力给出常用的球体和等值面绘制编程方法，并对Gemini表面活性剂自组装的耗散粒子动力学模拟给出了具体的结果。研究表明MATLAB不仅可以很好地绘制了模拟结果，也大大提高了编程效率。

关键词：MATLAB；分子模拟；可视化

中图分类号：TP391 文献标识码：A 文章编号：1009-3044（2017）30-0181-03

MATLAB Implementation of Visualization of Molecular Simulation Data

LI Jian， FENG Jian

（School of Material Science and Chemical Engineering， Chuzhou University， Chuzhou 239000， China）

Abstract： Visualization of the molecular simulation data is an important method to visualization description. In this paper， MATLAB is been used as a common programming method in the sphere and the isosurface rendering for the powerful graphics capabilities， and self-assembly results of the Gemini surfactant by dissipative particle dynamics simulation are given. The results show that MATLAB are not only good to draw the simulation results， also greatly improve the programming efficiency.

Key words： MATLAB； Molecular Simulation； Visualization

1 概述

計算化学或分子模拟研究中需要对体系的结构性质进行绘图，以便更形象地表示体系的演化或结构性质变化。很多计算化学软件带有自己的作图模块，如Material Studio。还有一些，较通用的可视化软件可供选择，如Rasmol、VMD等。尽管没有自带绘图的计算或模拟程序，如LAMMPS、GROMACS等，一般都有输出为常用可视化软件的数据格式接口。对于那些自行编制计算或模拟软件的化学工作者，一种选择这些通用绘图软件，但在也会有很多有不方便之处，尤其是对于粗粒化的模型或特殊的结构体系。这些化学工作者也需要编制与研究相关的可视化软件。

可视化软件编制既涉及专门的绘图语言也涉及具体工作的特定算法，目前主要有两种方法可供选择。一是DirextX，它主要面向Windows平台；另一种是OpenGL，它是跨平台的编程接口。这些方法的选择不可避免要涉及很多底层操作，编程人员也需要花费很多精力来学习。另外，一些特定的绘图算法编程难度也很大，如绘制等值面的Marching Cubes算法[1]。

MATLAB是一种集科学数据运算和图形处理的程序语言，它简单易用的特性给化学工作者提供了极大的方便。MATLAB有着强大的绘图能力，它通过对图形的线型、立面、色彩、光线以及视角等属性的处理，将计算数据的特性表现得淋漓尽致[2]，在图像处理方面应用广泛[3]。

本文主要讨论利用MATLAB的绘图接口编制程序绘制表面活性剂分子在水溶液的聚集的胶束形态。其数据来自于耗散粒子动力学（DPD）模拟[4]。其中主要涉及粒子和等值面绘制。

2 方法

2.1 粒子的绘制

粒子可以是具体的原子，也可以是一个粗粒化的粒子，如DPD模拟中那样。在分子模拟中绘制粒子是比较基本的操作。在MATLAB首先要创建球模型，调用语句为：

[x y z] = sphere（num）；

其中，x， y， z是系统创建球体自动分配的值，num是构造球体的“细腻度”。此参数可以不填，默认的是20，意思就是这个球面是20×20个小网格组成的，值越大，球面看上去越真实，但计算量也就越大，绘制速度也越慢。在实际应用过程中，可以首先设置一个较小的值，在汇报工作或撰写论文时再使用一个更大的值，绘制出精美的图像。

创建了球模型接下来就需要在坐标系中绘制它，调用的函数为：

surf（x0+x*r， y0+y*r， z0+z*r， color）；

该函数表示的是在（x0，y0，z0）处绘制半径为r，颜色为color的球体。其中的x， y， z就是sphere函数中的x， y， z值。对于这个函数的最后一个参数color，是指定球体颜色的参数。为了区分粒子，需要给每种不同粒子类型赋予不同颜色。以下是从一个数据文件，读取数据绘制球体的主要代码，其中数据文件由四列组成前三列为粒子的xyz坐标，最后一列为粒子类型。另外还需要从一个配置文件中读取粒子总数和不同粒子类型的直径大小。

fidData = fopen（fileData， 'r'）；

%将数据文件（n行×4列）读取到data矩阵中

data = textscan（fidData，'%f %f %f %f'）；

%从data各列依次读取坐标和粒子类型

x = data{1，1}； y = data{1，2}； z = data{1，3}；endprint

type = data{1，4}；

[rX rY rZ] = sphere（）； %创建球体模型

%将各粒子绘制在三维坐标轴中

for k=1：total

%type（k）是粒子类型

color = ones（size（X））；

color（：， ：， 1） = type（k）；

if target==type（k）

%在[x（k）， y（k）， z（k）]点作半径radius（type（k））的球体

surf（radius（type（k）） * rX + x（k）， radius（type（k）） * rY + y（k）， radius（type（k）） * rZ + z（k）， color）；

hold on； %保留当前绘图和坐标轴属性等

end

end

2.2 等值面的绘制

表面活性剂水溶液会形成不同的胶束结构，它有很多表面活性剂分子聚集而成。使用粒子图，由于胶束外部为各种粒子，不能很清楚地看出聚集体的轮廓，更难以反映不同聚集体的结构差别。为表现聚集体的轮廓图，常需要绘制其等值面。将粒子图转化为等值面图，需要在空间构建网格，并将粒子数据转换（分散）为网格点的数值，再通过这些离散的数值绘制等值面。构建网格数据需要根据具体的研究确定特定算法。

本文使用的算法是将模拟盒子分解成等分的小正方体格子，每个小正方体的顶点（即格点）的值初始化为0。当具有一定体积的某种类型的粒子占据该格点时，该格点的值赋值为1。然后将取值大于0.5的格点连接起来作等值面[5]。

在MATLAB中绘制等值面的函数为isosurface函数，调用格式为：

[fc vt] = isosurface（x， y， z， v， value， color）；

x， y， z指的是格点的坐标。V为格点的数据值，是一个三维矩阵，包含了所有点（x， y， z）的值，且值的多少与配置文件中规定的坐标轴范围有关。value指的是将哪个值连接成面，如果指定是0.5，那么isosurface函数会进一步对格点进行插值运行获得所有值为0.5的点，这些点可能处于这些元胞的定点、楞或面上，再将这些值连结起来绘制成值为0.5的等值面。一般说来，给定具体值的点在元胞上连结形成三角形，该值的等值面就是有很多个三角形组成，空间元胞分得越多，三角形就越多，等值面就越细腻，绘制工作量越大，计算开销越大。color指的是绘制面的颜色，可以用颜色代码来指定。

如果绘制一个基本的等值面，直接用上述的函数就足够了，为了对等值面进一步操作，而且光照及颜色效果更佳，则需要使用patch函数，调用格式如：

P = patch（‘Faces， fc， ‘Vertices， vt）；

另外，使用函数set（P， 'FaceColor'， 'green'， 'EdgeColor'， 'none'）可以改变表面的颜色和边沿的颜色，该语句使用的是表面为绿色（或RGB值[0 1 0]表示），无边沿。

%构建（scaleX scaleY scaleZ）网格矩阵

[X Y Z] = meshgrid（0：1：scaleX， 0：1：scaleY， 0：1：scaleZ）；

[rows cols heis] = size（X）； %获得刚定义矩阵的长， 宽， 高

V = zeros（rows， cols， heis）； %定义一个初始化为0的数据矩阵

%把粒子的坐标值转化成正数的新坐标

x = x - rangeMinX； y = y - rangeMinY； z = z - rangeMinZ；

%读取每个粒子

for i=1：total

%仅对type（i）粒子处理等值面，构建顶点值

if targetSur==type（i）

%坐标点直接转成格点

x_t = round（x（i）*scaleX/（rangeMaxX-rangeMinX）） + 1；

y_t = round（y（i）*scaleY/（rangeMaxY-rangeMinY）） + 1；

z_t = round（z（i）*scaleZ/（rangeMaxZ-rangeMinZ）） + 1；

V（x_t， y_t， z_t） = 1；

end

end

%繪制等值面

[face vertice] = isosurface（X， Y， Z， V， 0.5）；

P = patch（'Faces'， face， 'Vertices'， vertice）；

set（P， 'FaceColor'， [0 1 0]， 'EdgeColor'， 'none'）； %颜色设置

axis equal； %坐标轴单位相等

view（3）； %设定三维视点的默认值

light（'style'，'infinite'）； %光照设置

camlight right；

lighting phong；

axis （[0 scaleX 0 scaleY 0 scaleZ]）； %指定坐标轴大小

2.3 光照处理

尽管指定了体系中的每种粒子或等值面的颜色，但未必能看到它。就像黑夜里看不到各种物体，更别谈物体的颜色了。所以为了显示绘制的球体等对象，需要设置光照。它与真实世界一样，不同颜色光射在物体上，物体的颜色也有差别。只有白色光照反映物体的真实颜色，其它颜色光照，物体反映出来的颜色是由物体自身颜色和投射光颜色的叠加。设置光源的调用格式为：endprint

light（‘顏色， 颜色选项， ‘样式， 样式选项， ‘位置， 具体位置）；

光源的完整设置包括三个性质（选项），分别是颜色、样式和位置，次序任意。第一个性质是颜色字符，如r表示红色，g表示绿色。第二个参数设置光的类型，分为近光（‘local）和远光（‘infinite）两种类型。当选择近光时，与观察着相同距离平面上的粒子反光点不一样选择远光时，这些反光点是一致的。选择不同的样式类型，使得绘制的系统更真实。第三个选项，光源所在的位置，填写三维坐标。对于光照的角度也可以使用camlight right这样的指令，它表示光的照射方向在右边。

不同光源照射到同一物体有不同效果，如一个很大的平面光源和一个点光源差别就很大。距离平面光源不同位置的粒子其投影大小相同并等于粒子大小，而距离点光源的近的粒子投射阴影则更大。照明效果（算法）设置为：

lighting <选项>

其中的选项有，flat（平行光，对每个面使用均匀光）、gouraud（计算顶点法向量，再对穿越的每个面进行线性插值，用于曲面）和none（关闭光源）。

另外，物体的材质不一样，反射光不一样，看到的效果也不一样。如相同颜色的木制球体和金属球体，光在木制球体上产生的投射光点具有哑光性质、甚至没有反光点，而在金属球体上显得比较明亮。调用格式为：

material <选项>

其中选项有，shiny（较亮，反射光颜色仅取决于光源颜色）、dull（较暗，没有镜面亮点，反射光颜色仅取决于光源颜色）、metal（金属光泽，反射光颜色取决于光源和对象表面两者的颜色）和default（默认设置）。

如绘制完粒子代码后面追加如下光照语句：

light（'style'，'infinite'）；

camlight right；

shading interp； % lighting phong； %等值面使用该语句

3 结果

3.1 模拟细节

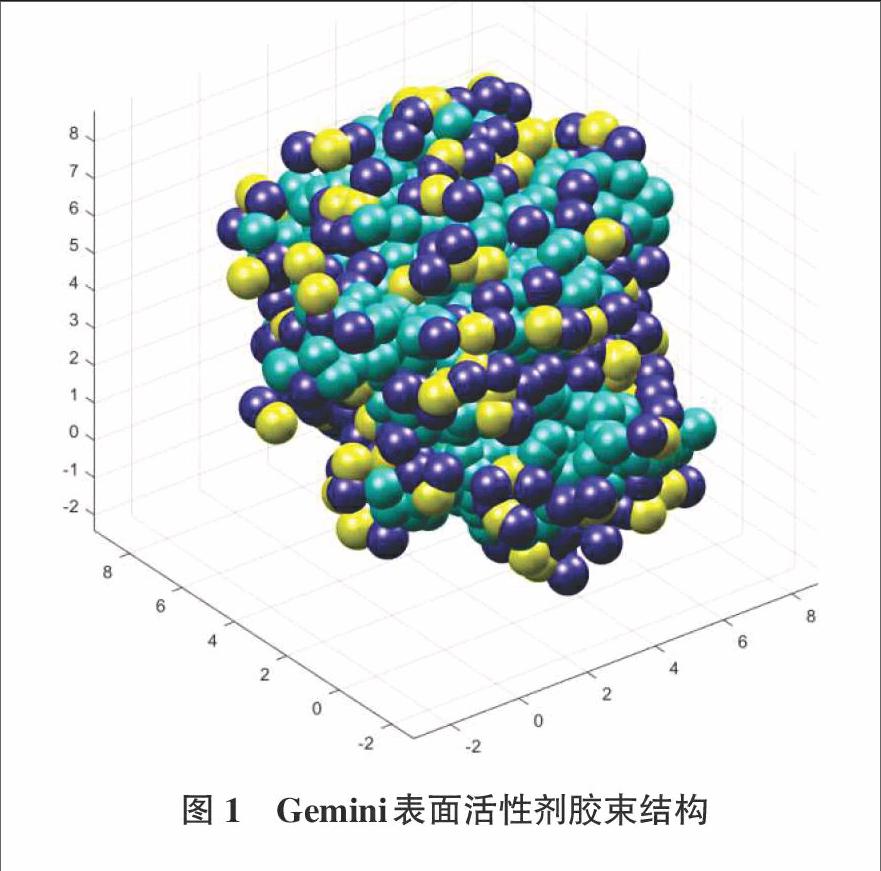
本文模拟的为Gemini表面活性剂在水溶液中的自组装行为。所谓的Gemini表面活性剂就是两种传统的表面活性剂的头基通过桥接基团连结在一起。本文粗粒化的Gemini表面活性剂结构为（B3A）3C，其中A是头基，B3为尾链，C为桥接基团。水分子使用W表示。表面活性剂的密度为0.05。模拟盒子为正方体盒子，长宽高均为20。所有相同粒子间的相互作用力参数为25，aAC=aAW=aWC=25，aAB=aCB=aWB=40。

3.2 粒子与等值面图

在本文给定的参数下，Gemini表面活性剂在水中形成了胶束。图1是仅对表面活性剂聚集体绘图，表面活性剂的所有基团都使用粒子呈现，为了显示更为圆滑的球体，sphere中的参数设为40。MATLAB绘制粒子图需要很大的运算量，如果对包含水的所有24000个粒子绘图，计算机显卡较弱时是无法绘制或响应时间很长。

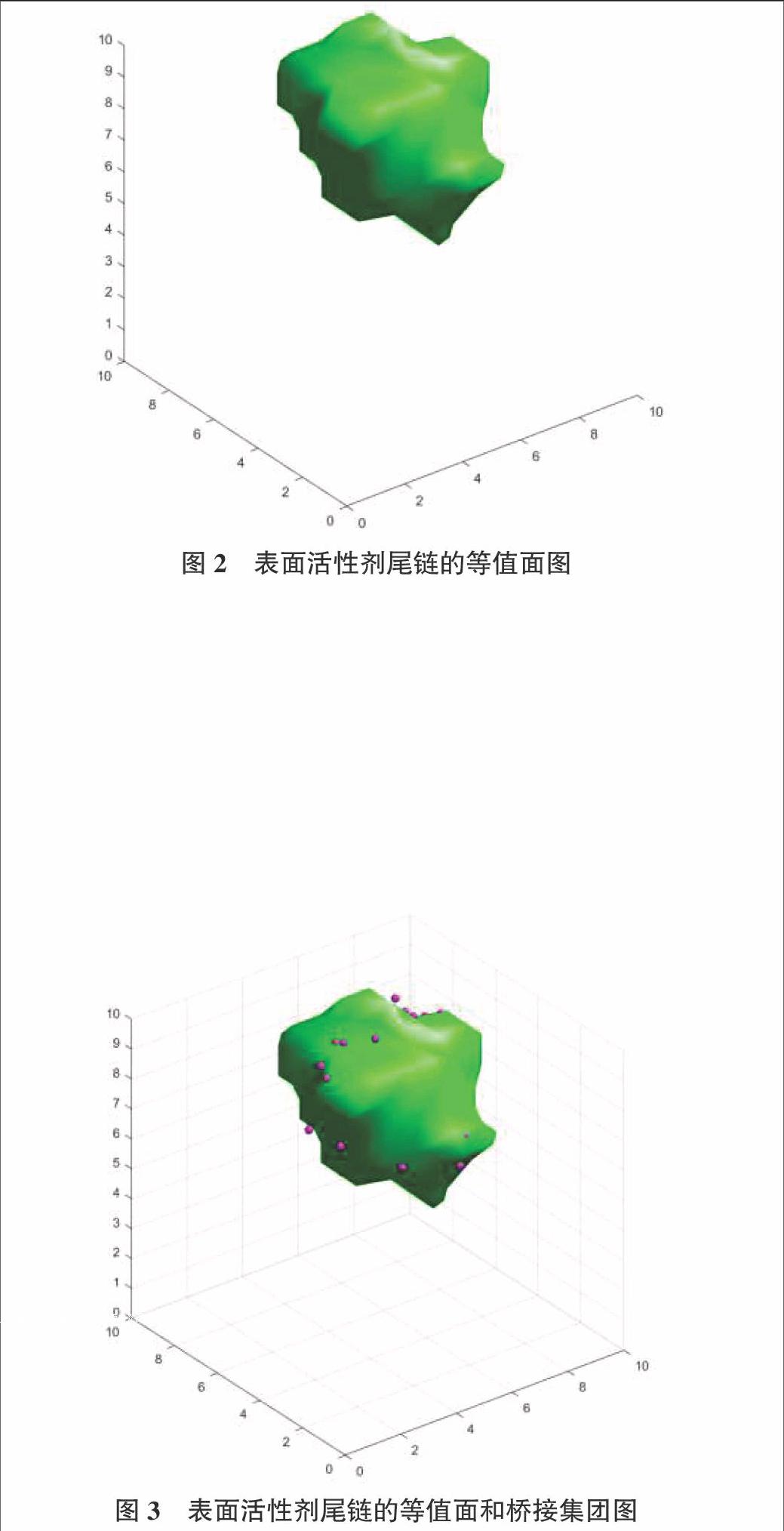
要想从图1中看出胶束的轮廓图是非常困难的。图2是选取表面活性剂尾链B值为0.5时的等值面图，从该图可以更清楚看出形成胶束轮廓结构。当然通过该图可以看出胶束的轮廓图过渡还是比较生硬，很多地方不够圆滑。则需要对由粒子坐标构建网格数据的算法进行调整。

单纯绘制粒子无法看清楚胶束的形态，仅仅绘制胶束的等值面图，往往只能就一种类型粒子进行。为了既能看清楚胶束轮廓，又能看到某些重要粒子的分布情况需要同时绘制等值面图和粒子图。在算法方面只需要将前面介绍的两种绘制方法的坐标轴设置为相同，并进行叠加即可。图3给出了体系的尾链的等值面和桥接基团的粒子图。本文选择的力常数表明桥接基团是亲水的，因而它在尾链聚集体的外侧，与水交接的界面层中。

4 结论

本文仅讨论了粒子和等值面的绘制方法，其他如化学键的棒状显示，以及某官能团的特定显示方法并没有提到，当这些特定的显示方法MATLAB均能做到。MATLAB将这些作图函数进行了高级别封装，极大降低了科学可视化的编程工作量。化学工作者进行相应研究工作时可以将更多的时间和精力放在特定问题的特殊处理上，从而更清楚地显示研究结果。

参考文献：

[1] Thomas Lewiner ， Hélio Lopes ， Ant?nio Wilson Vieira， Efficient implementation of Marching Cubes cases with topological guarantees[J]， Journal of Graphics Tools， 2003， 8（2）：1-15.

[2] 李丽， 王振领. MATLAB工程计算及应用[M].北京： 人民邮电出版社， 2001：47-106.

[3] 李卓，李益民. Matlab 与VC++混合编程技术在图像处理中的应用研究[M].电脑知识与技术， 2011，7（22）：5450-5452.

[4] Robert D. Groot， Patrick B. Warren. Dissipative particle dynamics： Bridging the gap between atomistic and mesoscopic simulation[J]. J. Chem. Phys. 1997， 107（11）：4423-4435.

[5] Robert D. Groot， Patrick B. Warren. Dynamic simulation of diblock copolymer microphase separation[J]. J. Chem. Phys. 1998， 108（20）：8713-8724.endprint