基于遗传算法的混合花粉算法

吴文斌++刘志锋++魏振华

摘要：花粉算法具有所用参数少，易调节，搜索路径优等特点，已运用于很多工程优化问题。但是存在易过早收敛、收敛速度慢和易陷入局部最优等不足，为了解决这些不足，对花粉算法做一些改进。在算法初期引入混沌序列做初始化，并在较优位置引入遗传算法的改进交叉和变异策略，提出一种基于遗传算法的混合花粉算法（Hybrid flower pollen algorithm Based on Genetic Algorithm）。对HGFPA 算法与FPA算法通过优化问题中4个典型复杂测试函数进行仿真实验对比，结果表明HGFPA 算法的收敛速度与精度均优于 FPA 算法。

关键词：混沌理论；遗传算法；混合花粉算法

中图分类号：TP18 文献标识码：A 文章编号：1009-3044（2017）30-0173-03

Hybrid Flower Pollen Algorithm Based on Genetic Algorithm

WU Wen-bin， LIU Zhi-feng， WEI Zhen-hua

（Information Engineering Institute， East China University Of Technology， Nanchang 330013， China）

Abstract： The pollen algorithm has many characteristics，such as less parameters、easy adjustment and excellent search path，and has been applied to many engineering optimization problems. In order to solve these problems ， the pollen algorithm to do some improvements. In the early stage of the algorithm to introduce chaotic sequence to do initialization，and the pollen gametes are used to initialize the pollen gametes. Then the improved crossover and mutation strategy of genetic algorithm is introduced in the optimal position. The HGFPA algorithm and the FPA algorithm are compared by four typical complex test functions in the optimization problem，the results show that the convergence speed and accuracy of the HGFPA algorithm are better than those of the FPA algorithm.

Key words： chaos theory； genetic algorithm； hybrid flower pollen algorithm

受啟发于自然界的花授粉行为，杨新社[1]在2012年提出了一种新型的启发式算法—花粉算法。该算法能够有效地解决很多单目标或多目标问题，并很好地运用于了某些工程设计等领域。

花粉算法一经提出就引起了很多学者的兴趣，很多人把它稍加改进并运用于解决实际问题。王正，何毅等[2]提出了一种基于监测邻域的改进花授粉算法（IFPA），在算法迭代中引入监测邻域概念，对邻域中的粒子，根据适应度指数定标确定不同粒子的选中概率，对部分粒子选择性变异，增加了粒子的多样性，加强了算法的效率。经过实验仿真，IFPA算法比其他智能算法在做PID控制器参数整定方面有更好的优势，寻优能力优于其他算法。

本文针对基本FPA在解决复杂优化工程实践问题时存在着收敛速度慢、容易陷入局部最优值的不足，而提出了一种改进的花粉算法（HGFPA）。在HGFPA的演化过程中，首先利用混沌理论作种群初始化，其次，在较优位置引入遗传算法的改进交叉和变异策略，加快收敛速度，增强算法逃离局部最优的能力。通过对一些演化计算领域内广泛使用的几个基准测试函数作仿真实验，验证了HGFPA的有效性。

1 基本花粉算法

花粉算法[3]具有参数少、实现简单、易调节等优点，能很好地平衡全局搜索与局部搜索之间的问题，全局寻优能力强，遵循四条准则：

1） 式（1）是全局授粉过程，生物异花授粉是带花粉的传粉者的全局授粉过程，其中L服从式（2）；

2） 式（3）是局部授粉过程，非生物自花授粉是传粉者的局部授粉过程；

3） 花恒常被认为是正比于两朵花相似性的繁殖概率；

4） 局部授粉与全局部授粉由转换概率p∈[0，1]控制。

[xt+1i=xti+γL（λ）（G*-xti）] （1）

其中：[xti]是花粉i在第t次迭代的位置，G*是目前发现的最优解，γ是控制步长的比例因子，L（λ）对应花授粉的强度。由于昆虫可能以各种步长移动一大段距离，Levy飞行可有效地模拟这种特性，也就是说， L（λ）>0。并且

[L→λΓ（λ）sin（πλ/2）π1s1+λ] （2）

其中：Γ（λ）是标准的伽马函数，它的分布对较大步长[s>0]是有效的。

[xt+1i=xti+ε（xtj-xtk）] （3）

其中：[ε]为在[[0，1]]内均匀分布的变量，这里[xtj]和[xtk]是来自相同物种但不同花的花粉。endprint

2 混沌序列初始化

花粉算法采用随机初始化的方式，这种方式容易导致花粉种群分布的不均匀。混沌现象具有非周期、自相似有序性的特点，它随机性、规律性、遍历性强。利于丰富种群的多样性，使算法容易跳出局部最优，非常适合与智能算法相结合使用[4]。其中混沌序列由式（4）的立方映射[5]产生，利于混沌序列初始化花粉配子位置。

[y（n+1）=4y（n）3-3y（n）；-1≤y（n）≤1；n=1，2...] （4）

3 基于遗传算法的混合花粉算法（HGFPA）

标准花粉算法通过搜索个体极值和群体极值完成全局极值寻优，虽然方法简单，且能够收敛，但是随着迭代次数的增加，在种群收敛集中的同时，各花粉配子也越来越相似，易陷入局部最优而无法跳出，混合花粉算法改变传统花粉算法中的利用跟踪极值来更新花粉配子位置的方法，引入遗传算法中的交叉和变异操作，通过花粉配子与个体极值以及群体极值的交叉和花粉配子自身变异的方式产生新个体，对产生的新个体采用保留优秀个体策略，只有在新花粉配子适应度好于旧花粉配子才更新花粉配子。通过这种方式来搜索最优解。

图1 混合花粉算法流程

4 改进的花粉算法流程

Step 1：混沌序列初始化花粉个体。

Step 2定义最大迭代次数Tmax ，λ，转移概率[p∈[0，1]]。

Step 3 对于种群中所有的n个花粉配子进行授粉：产生一个随机数rand，若rand < p，则以式（1）进行全局授粉；否则，以式（1-3）进行局部授粉。评价新解，若新解更好，则更新种群，找到当前的最优解G*。

Step 4花粉配子同个体极值和群体极值的交叉。个体和个体最优花粉配子作交叉获得新花粉配子，比较目标函数值，更新花粉配子，找出当前的最优解G*；把个体和群体最优花粉配子作交叉获得新花粉配子，比较目标函数值，更新花粉配子种群，找出当前的最优解G*。

Step 5若算法满足停止准则，停止迭代；否则转入Step 3。

Step 6 算法终止，输出全局最优值G*。

5 仿真实验与结果分析

5.1 参数设置与测试函数

本文比较FPA与HGFPA在4个Benchmark函数上的优化性能，4个Benchmark函数都是来自全局优化测试函数库[6]，如表1所示。各参数设置为p=0.8，[λ] =1.5。实验硬件环境为Intel?Core? with HD Graphics 4400 2.80 GHz ，4.00GB，操作系统Window 7，利用Matlab编程实现。

5.2 仿真实验与分析

5.2.1 实验1 HGFPA与FPA进化曲线对比

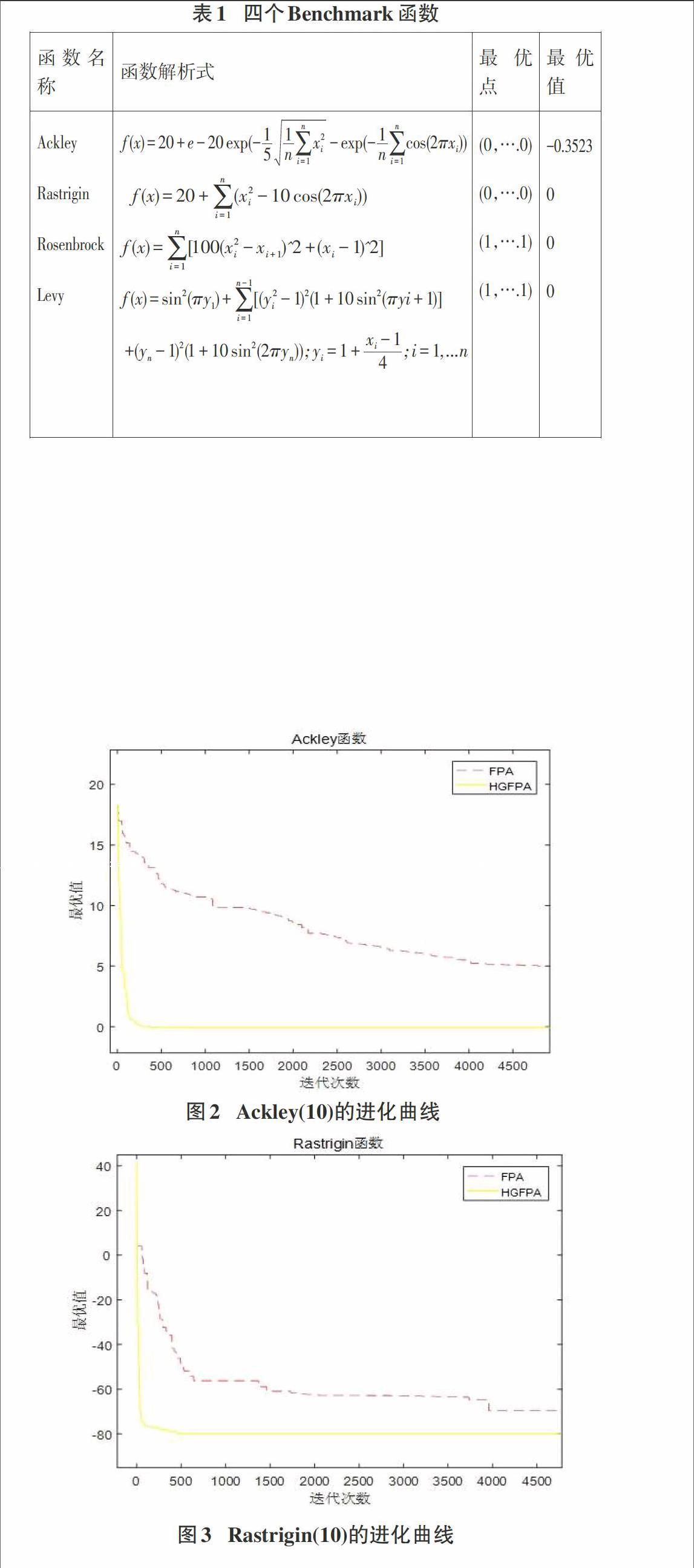
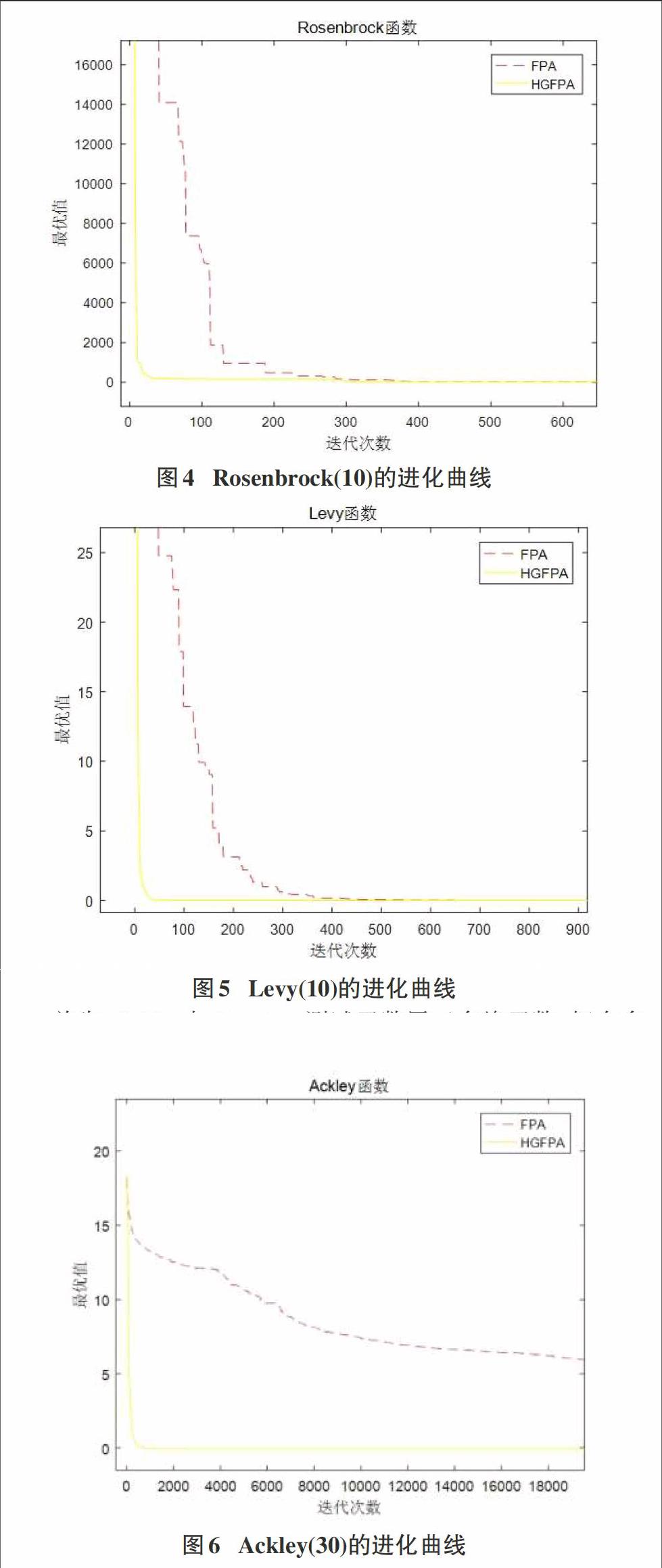
设置维数d=10、30，4个Benchmark函数的迭代次数Tmax分别为5000，20000。对4个Benchmark测试函数做仿真实验。在迭代次数为5000次时，测试函数Ackley（10维）的进化曲线如图1所示，测试函数Rastrigin（10维）的进化曲线如图2所示；测试函数Rosenbrock（10维）进化曲线如图3所示；测试函数Levy（10维）的进化曲线如图4所示。

首先，Ackley与Rastrigin测试函数属于多峰函数，拥有多个局部极值点，导致算法很容易地陷入局部最优，可以用来测试算法探索能力强弱。

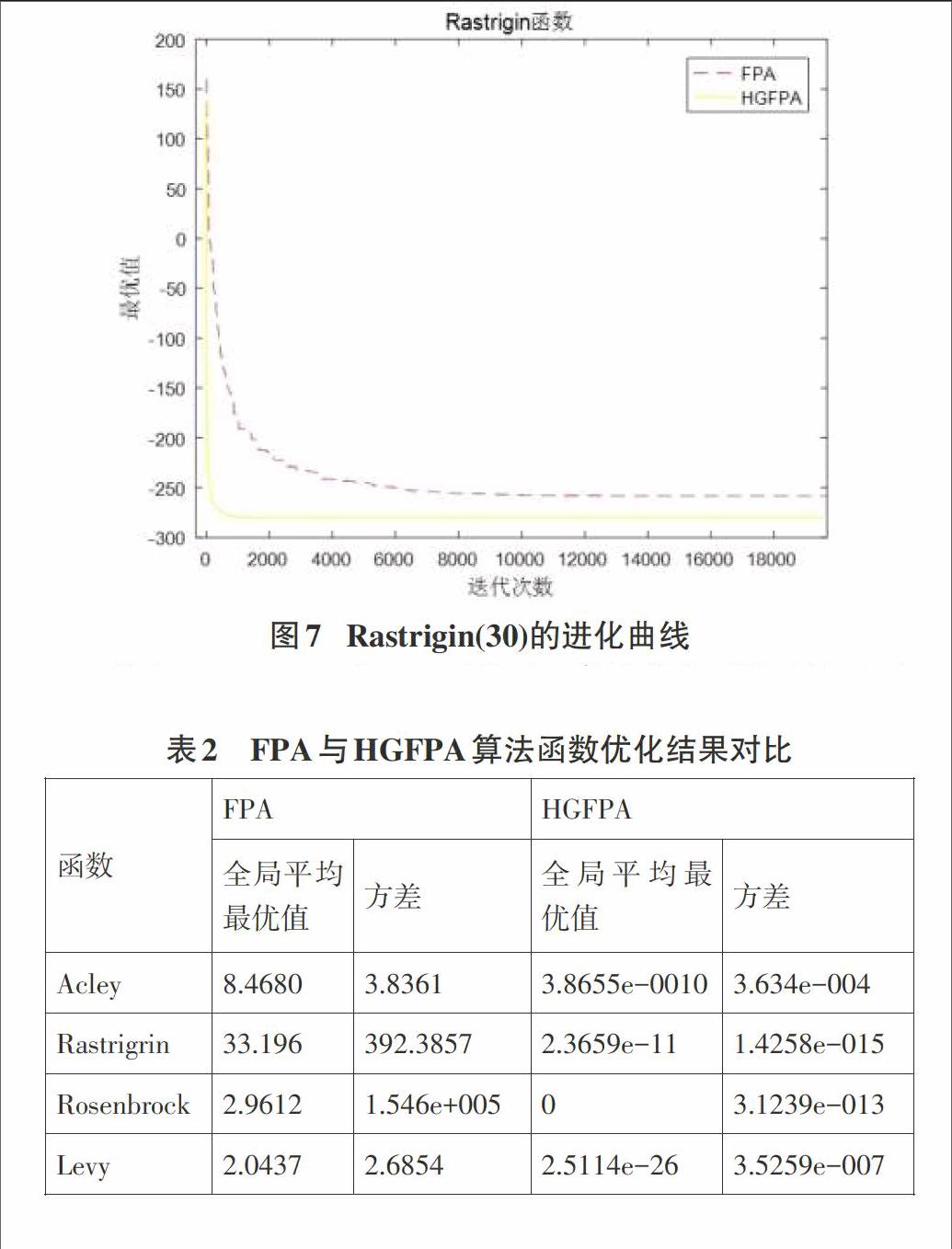
在图2和图3中， HGFPA与FPA两种算法收敛精度不同，HGFPA能够快速收敛且进度更高，HGFPA收敛到最优值的速度明显的优于FPA。经过实验发现（图6、图7），随着函數维数d的增加，算法收敛到最优点所需要迭代的次数也会随之增加，对于30维的Ackley函数，FPA的收敛效果与精度较差，在最大迭代次数之内不一定能收敛到最优点，从收敛速度和进度来讲，对于Ackley与Rastrigin函数，HGFPA算法的优化性能明显优于PFA。

其次，Rosenbrock与levy函数属于高维单峰函数，只拥有全局最优值，可以用来测试算法搜索能力的强弱。从图4和图5可以看出，对于Rosenbrock以及levy函数来说，尽管HGFPA与FPA两种算法收敛精度相同，但是HGFPA能够快速收敛。实验发现，与前面函数相似，HGFPA算法对于10维还是30维，算法都能够快速的收敛到最优点，但随着函数维数的增加，HGFPA算法收敛到最优点所需的迭代次数会随之增加，而FPA算法的收敛效果会变差，在设定的最大迭代次数下很难收敛到最优点。因此对于Rosenbrock与levy函数，HGFPA算法收敛精度与收敛速度均优于FPA算法。

综上可以得出，对于Ackley、Rastrigin、Rosenbrock、Levy这4个测试函数，从收敛精度与收敛速度来讲，HGFPA均优于FPA。

5.2.2 实验2 HGFPA与FPA算法函数优化结果对比

我们继续对HGFPA算法的优化能力做进一步的研究，在相同的实验参数下，对算法函数优化结果做对比，d=30，Tmax=10000，两种算法独立运行30次， 取这30次的平均值形成以下表格：

从表2可以看出，在测试函数30维时，对于全局平均最优值，HGFPA对于函数Ackley、Rastrigin、Rosenbrock和Levy的全局平均最优值明显优于FPA，HGFPA全局平均最优值与全局最优值很接近，因此，HGFPA算法的搜索能力明显优于FPA的搜索能力；对于方差，HGFPA对于4个测试函数的全局最优值的方差均小于FPA算法，说明在HGFPA算法的稳定性方面明显优于FPA算法，再次验证了HGFPA的优势。

6 结束语

本文在基本花粉算法上，针对搜索策略进行了改进。花粉算法的初始化过程中利用混沌理论对花粉配子的位置进行了初始化，使花粉配子分布更加均匀；在花粉配子最优位置添加了交叉操作和变异操作，增强算法逃离局部最优的能力，从而提高算法的收敛速度和算法的优化性能。实验结果表明基于改进搜索策略的混合花粉算法（HGFPA）比花粉算法（FPA）收敛到最优解所需的迭代次数少，收敛精度更高，大大提高了算法运行速度和全局平均最优值。由于花粉算法是新近提出的算法，可以与其他智能算法相结合，值得进行进一步的深入研究。

参考文献：

[1] Yang X S. Flower pollination algorithm for global optimization[M]. Unconventional Computation and Natural Computation， Lecture Notes in Computer Science， 2012， 7445： 240-249.

[2] 王正， 何毅. 基于改進花授粉算法的PID参数整定[J]. 计算机工程与设计， 2017， 38（1）：209-214.

[3] PAVLYUKEVICHI. Levy flights， norrlocal search and simulated annealing[J].Computational Physics， 2007， 6（8）：1830-1844.

[4] 刘召军， 高兴宝. 融合自适应混沌差分进化的粒子群优化算法[J]. 纺织高校基础科学学报， 2015， 28（1）：116-123.

[5] 冯艳红， 刘建芹， 贺毅朝. 基于混沌理论的动态种群萤火虫算法[J]. 计算机应用， 2013， 33（3）：796-799.

[6] JAMIL Momin， YANG Xinshe. A literature survey of benchmark functions for global optimization problems[J]. International Journal of Mathematical Modelling and Numerical Optimization， 2013， 4（2）：1-47.endprint