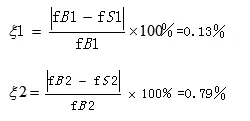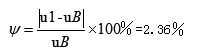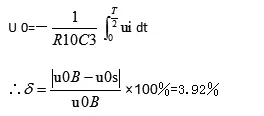正弦波-方波-三角波产生电路的设计与仿真
新疆大学机械工程学院工业工程系 黄 婧
正弦波-方波-三角波产生电路的设计与仿真
新疆大学机械工程学院工业工程系 黄 婧
针对正弦波-方波-三角波三者之间转换时由于电路复杂而导致波形易产生畸变的问题,设计出了可通过自行选频、调幅来进行转换的电路,实现了三种频率可调、清晰完整、未畸变波形的实时转换,使得波形频率连续,并且能产生符合设计要求的幅值,考虑到频率和容抗的关系、影响阈值电压跃变的外界干扰、二极管的特性,通过仿真,可以证明所提出的电路转换方式可行,并且解决了波形失真问题,从而有效的降低了波形畸变几率,提高了波形转换后的准确性.
选频;调幅;波形转换;仿真
引言
常见的正弦波-方波-三角波转换电路,由于电路复杂,所以导致波形不完整、容易产生畸变的原因有很多[1].现在将该波形产生电路分成三部分,即RC振荡电路产生正弦波,迟滞电压比较器实现正弦波-方波转换,积分电路实现方波-三角波转换.在第一部分电路中,通过选频和调幅环节,在放大电路中引入正反馈,并创造使其可以产生稳定振荡的条件.在第二部分电路中,通过迟滞电压比较器,预实现正弦波到方波的转换.虽然固然单限比较器相对活络,可是它的抗干扰本领比较差.而滞环电压比较器具有迟滞的特征,也便是惯性,更具备必然的抗干扰本领,故选择滞环电压比较器来完成此项转换.在第三部分电路中,我们将反馈电阻用积分电容代替,构成积分电路,实现方波到三角波的转换.基于Multisim软件仿真后,证明该电路转换可行,并且有效的解决了波形失真问题,降低了波形畸变效率.
1.工作原理
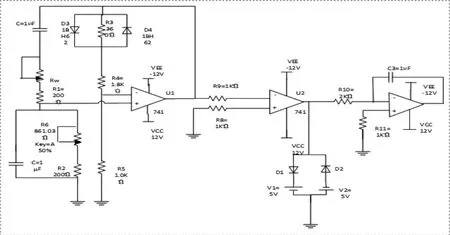
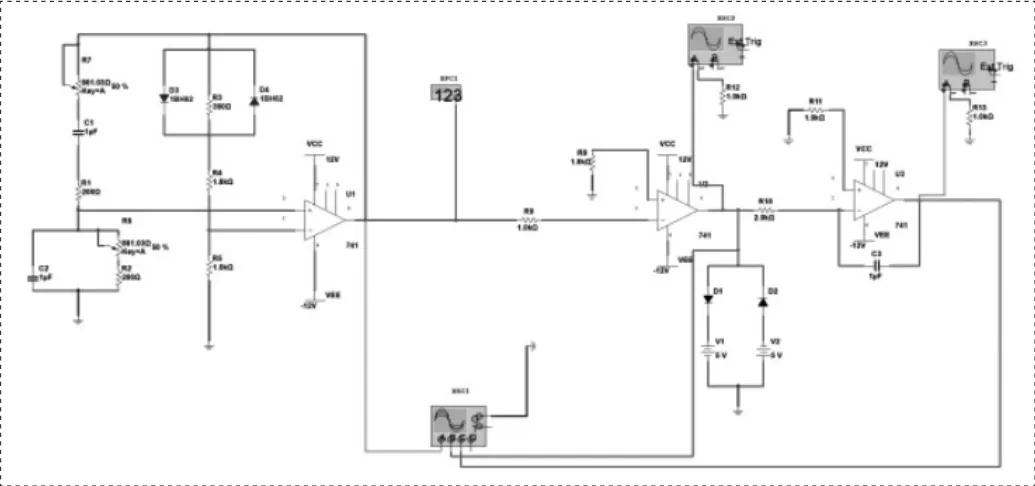
图1 电路原理图
a.选频环节:
确定电路的振荡频率,以确保电路产生正弦振荡.输入电压是放大器电路的输出电压:

使虚部为0,变为纯电阻电路,选频就结束了,即: R=Xc
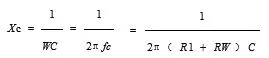
参数R、C的值均与振荡的频率有关,而放大电路中输入电阻的值在一定程度上也会影响RC的值;在实验的电路板中,电容、电抗会对频率造成影响,从而产生误差;能否起振、是否失真均与放大倍数息息相关,而放大倍数又与负反馈相关,负反馈越强其放大倍数就越低.当放大倍数大于3时就会存在失真;远远大于3时,输出的为类似方波;小于3时,无法起振.
b.调幅环节:
非线性环节,其作用是输出幅值稳定的信号.
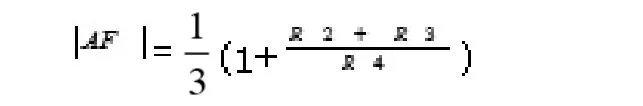
c.迟滞电压比较器
u + u +>u-时,输出正饱和: u 0=+U0(sat) 联系二极管单向导电的特征:输入正向电压时,二极管D1导通,输出正向电压5V;输入负向电压时,二极管D2导通时,输出负向电压-5V.即可得到幅值为±5V的方波.[3]当运算放大器在饱和区发挥作用时,两个输入端的输入电流均为零.此时理想运算放大器的开环电压放大倍数Auo→∞,因此,其线性区为一与纵轴重合的直线. 集成运算放大器同时又是一个线性放大元件.由于Auo很高,所以即使输入毫伏级以下信号,也足以使得输出电压达到饱和,饱和值为+UO(SAT)或UO(SAT),最终使其达到接近正电压电源或负电压源电压值;又或者说,因为干扰的存在,它的工作难以趋于稳定.以下图所示: d.积分电路 在反向比例运算电路中,我们将反馈电阻RF用积分电容CF[4]代替后,则构成了积分预算电路.根据"虚短"和"虚断"观点,输出信号u 0与输入信号u i的积分成比例. 当积分时间足够大时,u 0最后达到负饱和值-U0(sat).此时电容C3不再充电,相当于断开,负反馈此时将不复存在,随之集成运算放大器在非线性区进行工作. 电路原理图是彼此建构的Multisim软件和电路模拟[5].Multisim可以在板级的模拟、数字电路板的设计中得到的极好的应用.它所具备的电路原理图的图形输入与电路硬件描述语言的输入方式,使其具备丰硕的仿真阐发本领. 图2 仿真电路图 图3 正弦波-方波-三角波综合波形图 (1)正弦波频率误差分析: 在设计技术参数中要求产生的正弦波频率在150HZ~250HZ范围内根据这个范围所搭建的实际仿真电路中的频率为149.8HZ~251.97HZ. ∴频率的误差为: (2)方波幅值误差分析: (3)三角波幅值误差分析: 综上所述,经过仿真之后可证明该电路可行,且能满足既定的幅值和频率要求. [1]武立华,黄玉,王姣,赵恩铭,刘志海. 基于CPLD的正弦波/方波互换电路及实验[J].物理实验,2014,34(03):31-35.. [2]杨凯.基于虚实结合实验室的电路原理实验[D].浙江大学,2013. [3]徐静萍.具有带隙结构的迟滞比较器电路设计[J].现代电子技术,2011,34(06):160-162. [4]邵霞,彭红海,周有庆,戴瑜兴,王娜.用于电流型电子式电压互感器的积分电路[J].电子学报,2014,42(02):405-410. [5]付扬.Multisim仿真在电工电子实验中的应用[J].实验室研究与探索,2011,30(04):120-122+126.2.仿真
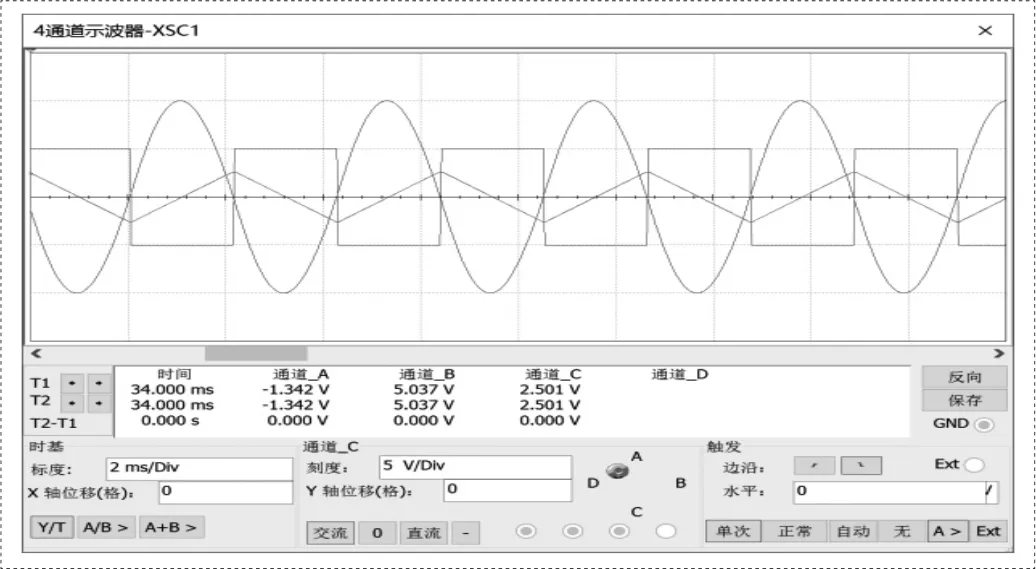
3.仿真结果分析