基于倒置声学基阵的INSUSBL组合导航算法研究

徐 博,郝 芮,王 超,张 勋

（哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001）

基于倒置声学基阵的INSUSBL组合导航算法研究

徐 博,郝 芮,王 超,张 勋*

（哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001）

文中关注水下潜航器导航定位时，电磁波传播途径中能量衰减、惯导系统长航时积累误差以及提高水下潜航器定位精度等问题。基于倒置的超短基线声学基阵，分析声波往返传播时间（RTT）、平面波近似方法和USBL导航解算方法及其坐标转换过程，结合INS误差方程，建立INS/USBL松组合模型。为进一步提高系统精度、动态性能和抗干扰性，考察USBL的原始斜距、斜距差以及声学基阵的空间分布信息，提出基于USBL原始输出信息的INS/USBL紧耦合组合导航方法。通过MATLAB仿真对导航算法进行验证，结果表明两种算法能充分抑制纯惯导误差随时间积累问题，且有效地估计出姿态、速度和位置误差角；其中紧耦合方法状态估计误差最小，导航参数精度相对松组合提高30%以上，对于提高水下载体导航定位精度、海洋探测具有重大意义。

组合导航算法；惯性导航系统；超短基线定位系统；紧组合技术

海洋覆盖地球大部分表面积，其中的能源和矿产资源丰富，因此海洋探测与开发、海洋仪器设计与制造具有极高的经济价值和战略意义，其中不容忽视的重要问题就是水下潜航器的定位问题[1]。惯导系统（inertial navigation system,INS）给载体提供完备的姿态、速度和位置等导航信息，短时间精度高，隐蔽性好，常用做主导航设备[2-4]。为解决长航时其误差随时间积累问题，常将惯导与其他导航方式组合。

声波在水下传播时要比光波和电磁波能量衰减都小，传播距离更远。常用的水声基线定位方式有长基线、短基线、超短基线等，其中超短基线以其基阵尺寸小、使用灵活和安装方便等优点而广泛应用，更契合水下定位对导航系统的严苛需求。常用的超短基线定位系统主要由发射换能器、应答器、声学基阵组成[5-6]。船底的换能器发射询问信号至水下已知位置的应答器，然后应答器发射应答信号被声学基阵的各个水听器接收，从而得到目标的定位信息。

Jalving B利用KF(Kalman Filter)技术把USBL（Ultra Short Base Line）和惯导系统的输出信息进行数据融合和滤波处理得到导航信息[7-8]。M Morgado采用直接法反馈校正的扩展卡尔曼，补偿系统的随机漂移误差，提高了导航精度[9-10]。国内学者李守军基于Kalman Filter的INS/USBL水下导航技术，只是简单的进行系统模型的研究、误差分析等，没有对紧组合进行深入研究[11]。张亚文提出的三应答器SINS/USBL紧耦合导航算法[12]针对INS到USBL的测角误差及安装角误差对导航精度的影响。其三应答器紧耦合方法的导航误差仿真结果相对于单应答器精度并没有明显提高，只是相对平滑，稳定性提高，对于应答器数目还有硬性要求。因此要达到实际应用精度还需要研究一种新的INS/UBSL耦合技术及导航算法。

本文针对针对自主性很高的水下潜航器，介绍超短基线定位原理，推导基于位置量测坐标转换的松组合INS/USBL状态、量测方程。通过测量声学信号从应答器到达接收声学基阵阵元之间的传播时间和相位差来解算目标的斜距和方位角[10]。考察USBL的原始斜距、斜距差以及声学基阵的空间分布信息，结合惯导系统误差方程，推导INS/UBSL紧组合量测方程。该紧耦合方法可以大大减少位置和方位角的滤波解算，且输出信息的误差形式较为简单且易于剔除。计算机仿真结果验证了该算法的可行性，对于工程实际中提高导航系统精度、动态性能和抗干扰性具有重要意义。

1 超短基线定位系统的定位方法和误差分析

1.1 USBL基于相位差的定位原理

建立基阵坐标系oxyz，设定基阵阵元的间距为d，4个水听器分别位于两个相互垂直的基线上（即x轴和y轴），其中心位于坐标原点，其坐标为(±d/2,±d/2)，目标位于 T 处，其坐标为（xa，ya，，za即为目标的深度。USBL的定位原理图如图1所示。θx,θy为位置矢量与x轴和y轴的夹角，位置矢量的模||为斜距。目标的位置矢量为→R，它与目标的坐标(xa，ya，za)的关系为：

在oxy平面内，位置矢量的投影为水平距离r，与x轴的夹角为目标的水平方位角：

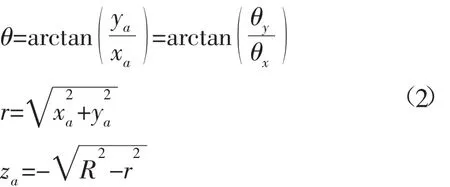
声学基阵尺寸较小，考虑到远场接收目标的声学信号，根据平面波近似视入射到声学基阵中各基元的声波平行。假设已知声波的波长为λ，φx,φy为

图1 超短基线定位系统的定位原理图

位于x轴和y轴上水听器接收信号的相位差，有：

将式（3）代入式（1）解得：

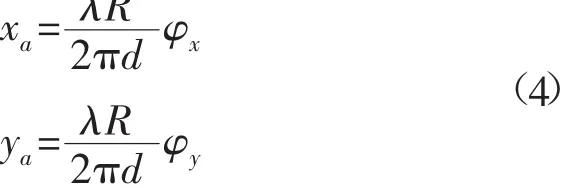
式中：R=c·Tri/2；c 为水中声波传播速度；Tri为换能器发射询问信号到接收到目标应答信号的时间。

测量USBL的φx,φy,c,Tri等参数值后，可以解算出目标相对于基阵坐标系的水平位置(xa，ya)、声波入射角θx，θy、水平方位角θ和斜距R等。由式(1)和式(2)可得目标在垂直方向的坐标（即目标的深度）为：

1.2 USBL导航解算方程

1.2.1 声波往返传播时间（RTT） 声波往返传播时间是由安装在载体上的换能器发射询问信号至预先放置在已知位置的应答器，然后应答器发射应答信号并被声学基阵的各个水听器所接收这一过程确定的；考虑声学系统的采样与量化。

声学基阵中各个水听器测量的声波往返传播时间为：

式中：t¯p为换能器至应答器的标称传播时间；t¯ri为应答器至第i个水听器的标称传播时间；[·]Ts表示声学系统的采样量化公式；Ts为声学系统的采样周期。误差项εt,εc分别表示询问信号和应答信号的测量噪声，εdi为水听器捕获应答信号时额外的微分误差，它远小于时间序列中的共模误差，应答延迟时间td视为已知，可方便地从总测量时间中剔除。

Miller考虑载体在静止或低速运动状态下，忽略由于换能器和水听器与应答器之间的相对运动所引起的询问信号和应答信号传播时间不同，简化后第i个水听器与应答器之间的声波传播时间为：

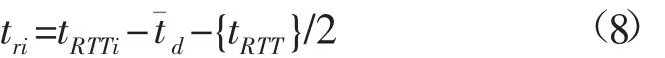
式中：{tRTT}为测量的所有声波RTT的平均值；它们之间的斜距测量值为：

式中：vp为水下声波的传播速度；ηc表示斜距的测量噪声。

1.2.2 平面波近似法 超短基线定位系统求解应答器的方向时，利用平面波分析法将水声信号近似为平面波，如图2所示，将三维波形转化到二维平面上。

取声学基阵的几何中心O，第i个水听器距离几何中心的位置矢量为bi∈R3，那么所有水听器的位置矢量满足Σbi=0。

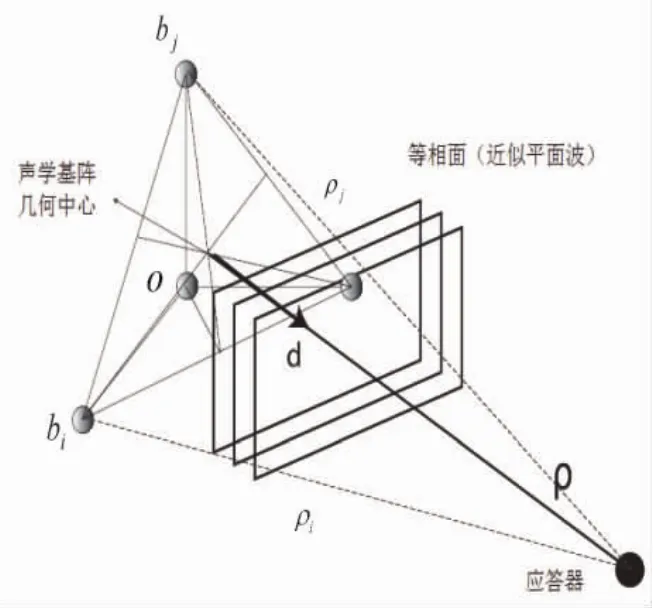
图2 水声信号平面波近似化

利用平面波近似法，任意两个水听器之间的斜距差均可由位置矢量差和方向矢量d确定，即有：

依据整体估计误差最小原则，使上式满足：

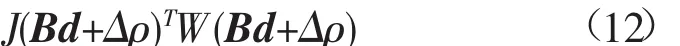
式中：W为权值矩阵，利用加权最小二乘法求解方向矢量d为：

式中：B+为矩阵B的加权广义逆矩阵，定义为B+(BTWB)-1BTW

对于某一应答器和声学基阵，确定一组线性无关的斜距差Δρ就能够对应计算出唯一的方向矢量。以声学基阵的几何中心为原点，结合式（9）计算的应答器到声学基阵的斜距，可得应答器相对于超短基线定位系统的位置为：

1.3 USBL导航解算方程的坐标转换

式（14）是基于超短基线定位系统解算的，转换到载体坐标系时需要坐标变换。取声学基阵中水听器的几何中心为超短基线定位系统坐标系（u系）的原点，取oxtytzt为东北天坐标系，u系的x,y,z三坐标轴分别与载体坐标系（b系）的坐标轴平行（声学基阵的偏移和安装误差角等误差项为零时，u系与b系完全重合）。组合导航定位时，u系（b系）、t系和e系三者之间的关系如图3所示，则应答器的位置矢量为：

考虑到Ou位于声学基阵的几何中心，则在USBL坐标系（u系）中水听器的位置矢量Ubi∈R3满足：

图3 USBL系统坐标框图

n为声学基阵中水听器的数量，一般为4个或者8个。考察u系与b系之间的关系，假设Ux为一矢量x在u系中的表达式，为u系到b系的转换矩阵，Bp0为u系的坐标原点到b系坐标原点的偏移量，则该矢量在b系中的表达式为：

公式变换为：

暂不考虑机动状态下，u系与b系未完全重合带来的误差因素，如受载体变形等影响，超短基线定位系统中第i个水听器对应答器的定位斜距为：

Ur∈R3表示应答器在u系中的位置矢量。

将式(18)代入到式(19)中解得：

bi∈R3表示第i个水听器在b系中的位置矢量。将式(15)代入式(20)解得：

2 INS/USBL组合导航系统的数学模型

2.1 INS/USBL松组合导航系统

（1）松组合导航系统的状态方程

组合导航系统的状态方程X˙=FX+W。

选取位置误差 δL，δλ，δh、东北天方向上的速度误差 δVE，δVN，δVU、东北天方向上的平台误差角 φE，φN，φU、沿载体坐标系x,y,z轴上的陀螺仪的随机漂移 εx,εy,εz和加速度计的零偏作为状态量，F，W分别为INS系统矩阵、系统噪声。

（2）松组合导航系统的量测方程

地球坐标系（e系）中，载体位置信息表示为p=[L λ h]T，其与地球直角坐标(x,y,z)关系为：

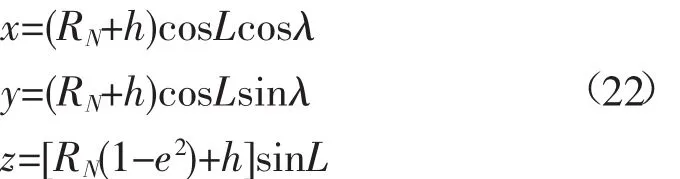
上式求解全微分得：

取INS与USBL的位置之差作为外部观测量，由式（3）得超短基线定位系统估计应答器的解算位置在载体坐标系中表示为：

nr为USBL位置测量噪声，向量形式如下：

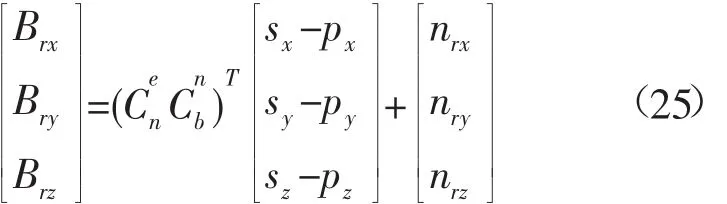
在导航解算过程中，INS能够估算出载体在地球坐标系中的位置和旋转矩阵，满足：

INS估算出应答器的位置信息在载体坐标系中表示为：

其向量形式为：

由惯性导航系统的误差方程得δp和R^RT，其中[φ×]为姿态误差角三个分量构成的反对称矩阵：

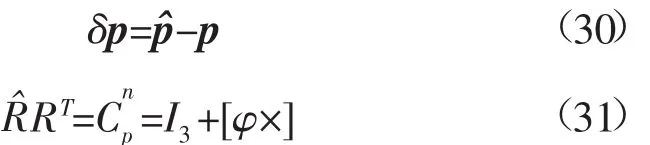
将上式代入到式（28）忽略二阶小量[φ×]δp得：

由式（24）、式（28）和式（32）可得 USBL与惯性导航系统解算的位置信息差值为：将地球坐标系中的直角坐标转换为经纬度和

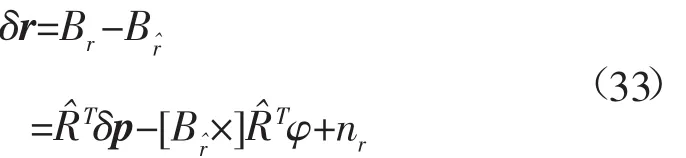
高度坐标，其向量形式为：

将其写为矩阵等式则有：

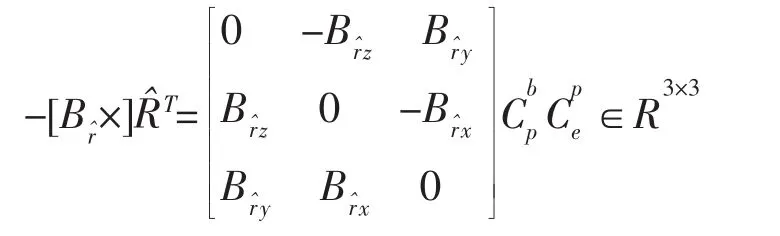
建立量测方程Z(t)=H(t)X(t)+V(t)观测矩阵如下:

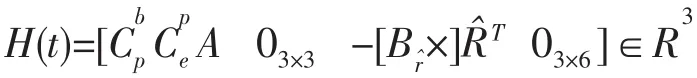
2.2 INS/USBL紧组合导航系统

USBL紧耦合只需提供斜距、斜距差等原始信息，减少了位置和方位角的滤波解算，输出信息的误差模型简单且易于剔除，对组合滤波算法的滤波结果更有益。

泰勒展开，取前两项得：

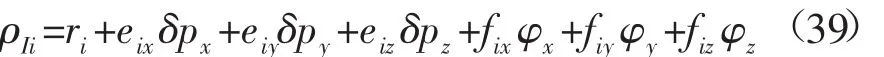
式中：ri，eix，fix如下，eiy，eiz，fiy，fiz同理。

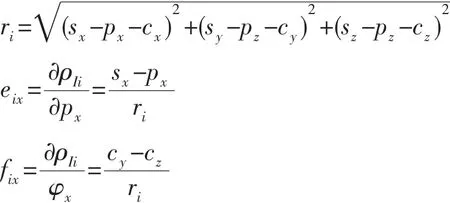
USBL中第i(i≤n)个水听器距离第j个应答器的斜距为：

斜距测量值之差为：

设声学基阵中有4个水听器，则有：

外部量测量斜距差的量测方程为：

设第i(i≤n)个水听器距离第j个应答器的斜距为 ρi，由式（21），（30）与（31）得：

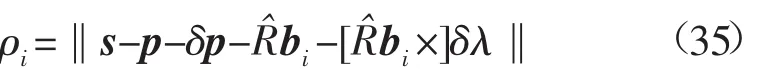
引入列向量符号，记为：

对特定某个水听器进行研究，将式（35）化为等式形式，可得：

量测噪声为零均值高斯白噪声，HIU如下：

考虑声学基阵水听器之间的空间分布，第i(i≤n)个水听器距离第j个水听器的斜距之差为：

声学基阵中有4个水听器之间的斜距差为：

则外部量测量水听器之间斜距差的量测方程为：

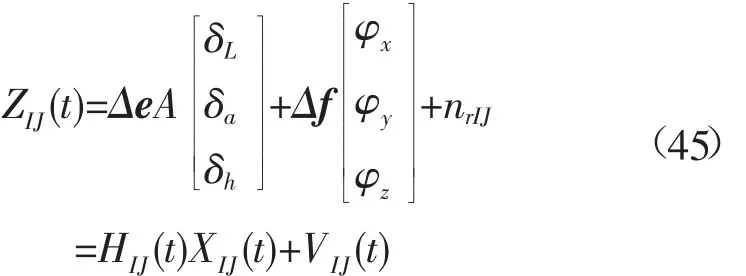
量测噪声为零均值高斯白噪声，HIJ如下：

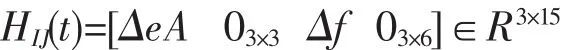
3 数值仿真与分析

为验证文中算法有效性进行如下仿真，导航误差参数如表1所示。惯性导航系统的初始水平和方位失准角分别为0.2°,0.2°和0.5°，考虑到滤波收敛速度，将初始速度误差和位置误差设为0；其中一个应答器的位置坐标设定为(0,200,0)，单位为m；USBL声学基阵的空间分布，如图4所示，u系的原点在b系的位置为Bp0=[0 0.3 0]T，4个水听器在u系中的位置为：

表1 导航系统的参数值

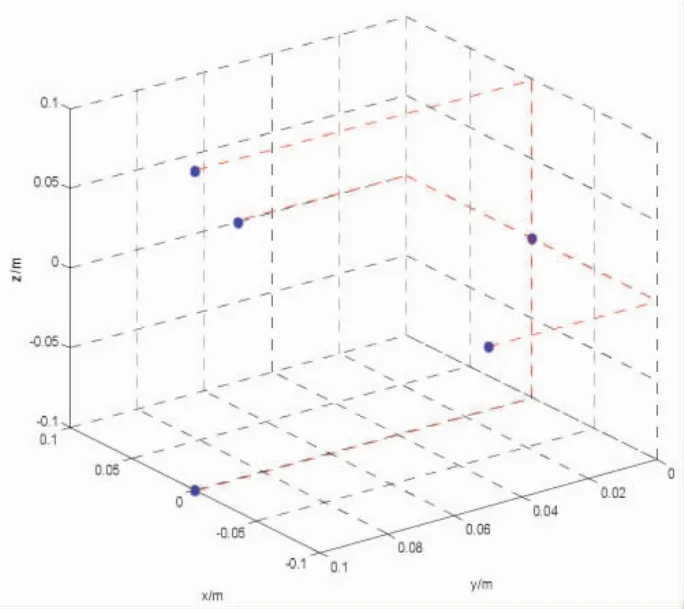
图4 声学基阵空间分布

松组合的量测噪声矩阵的初值如下所示，紧组合时只需将其维数扩展到m即可。

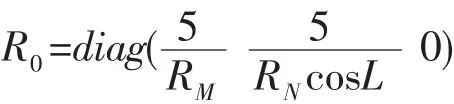
设定滤波解算周期为0.1 s，仿真时间为480 s，航行轨迹的初始位置为纬度 45.779 6°，东经126.670 5°，分别对松组合和紧组合导航算法进行仿真，理论航行轨迹如图5所示。

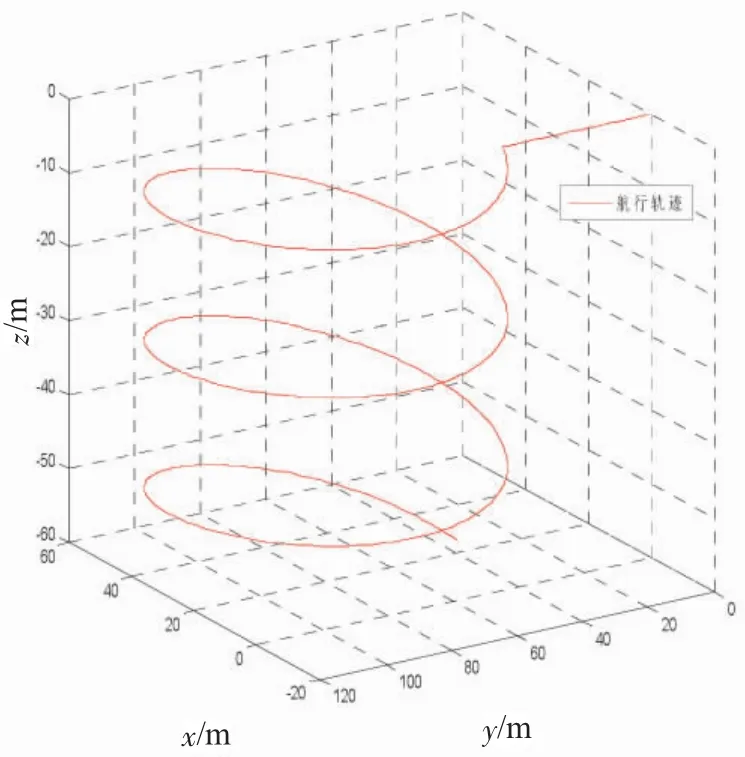
图5 航行轨迹

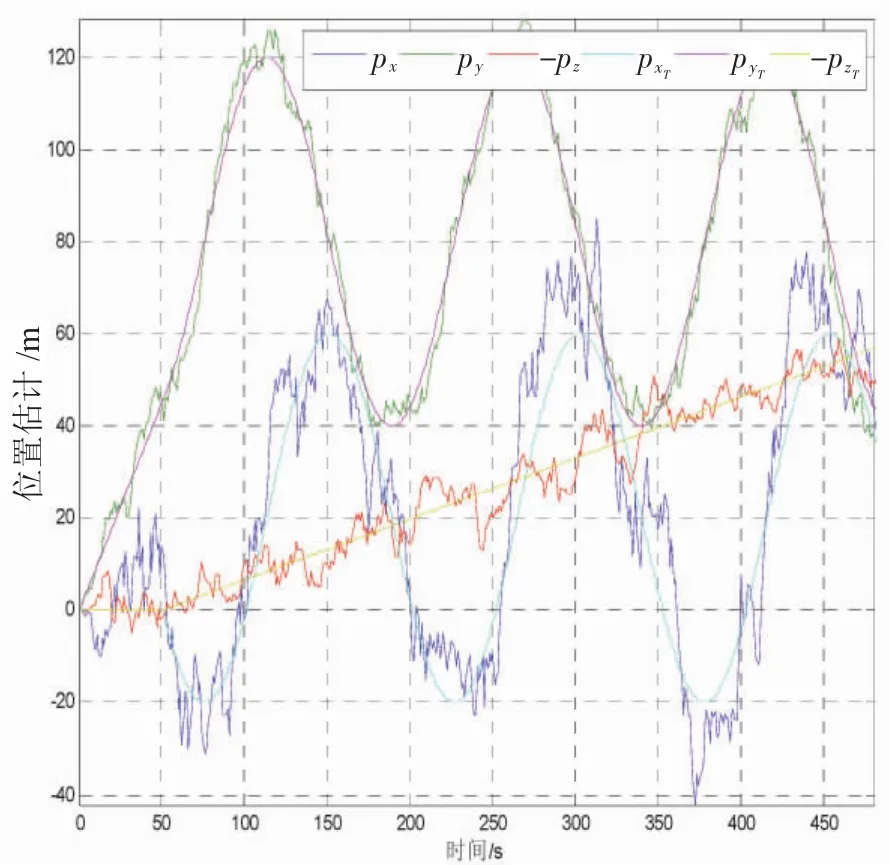
图6 松组合导航系统的位置估计曲线

作为对比，松组合和紧组合导航系统的位置曲线由图6～7所示，组合导航系统解算的姿态角、速度和位置误差曲线分别如图8～图10所示。

图7 紧组合导航系统的位置估计曲线

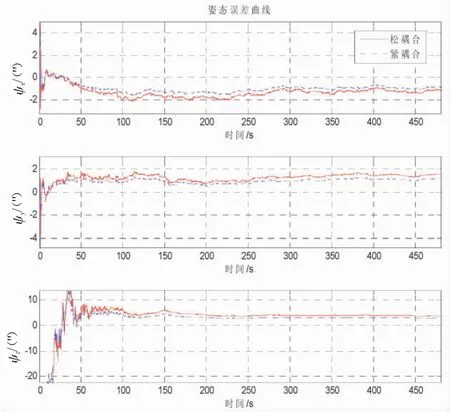
图8 姿态误差曲线

表2 姿态、速度和位置的误差值

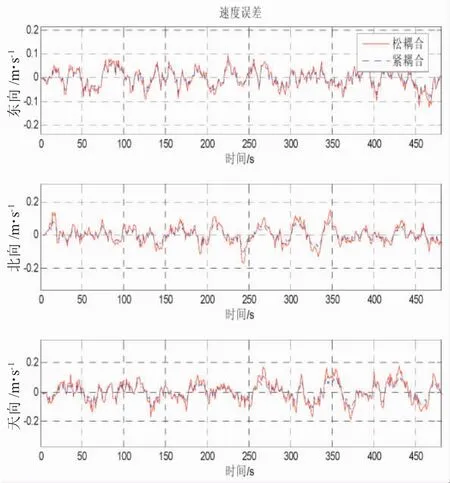
图9 速度误差曲线

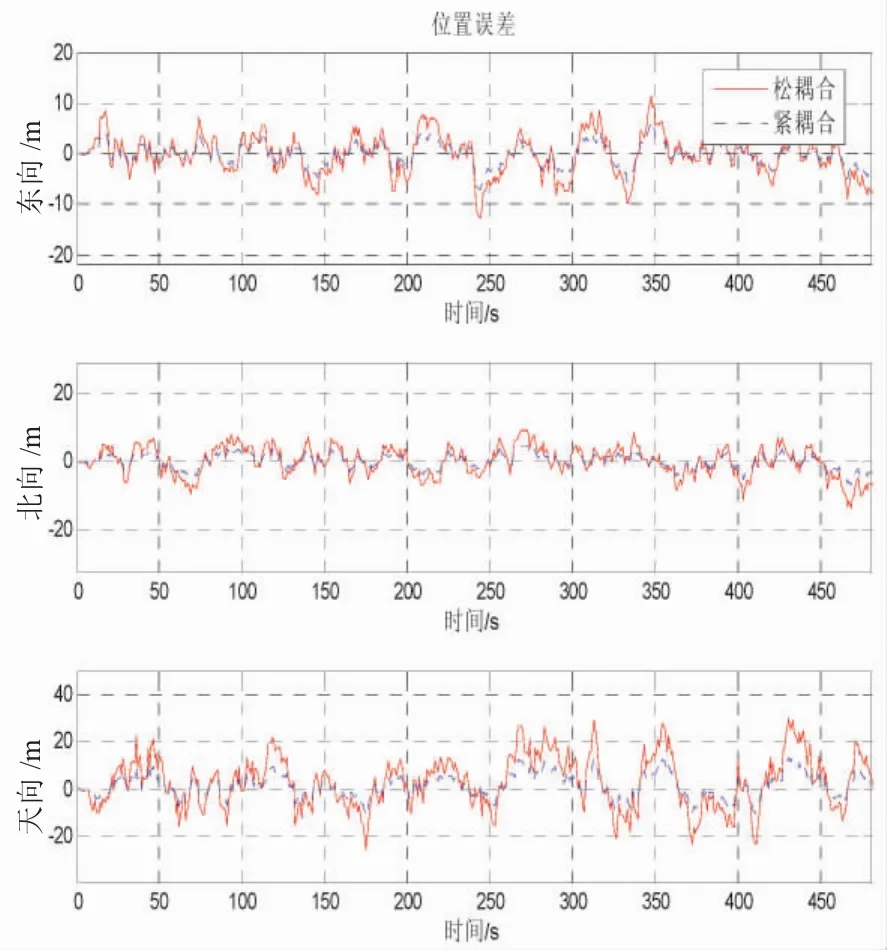
图10 位置误差曲线

将上述仿真曲线的误差值（RMS）进行统计整理，如表2所示。

通过对以上仿真曲线和表格的分析可知：

（1）虽然受到各种噪声和误差等因素的影响，将超短基线定位系统的定位信息与INS解算信息融合后，松耦合与紧耦合有效地抑制了纯INS速度和位置估计误差随时间逐渐累积发散问题，且能有效地跟踪载体位置信息，说明该算法的有效性。

（2）系统输出的姿态、速度和位置误差参数均能得到大幅改善，两种组合方法均能够有效地估计出各个误差角，从而提高整个导航系统的估计精度。

（3）通过对比图6～图7可以看出，紧耦合方法的位置估计相对实际航行轨迹波动最小，滤波效果更加平稳；从图8～图10以及表2的姿态、速度和位置误差RMS值可以看出，紧组合方法的导航参数姿态、速度和位置的估计误差更小，导航参数精度相对松组合平均提高30%以上，说明基于考察USBL原始输出导航参数的紧耦合方法对于进一步提高组合导航系统定位精度具有重要意义。

4 结论

本文针对水下载体高精度导航定位问题，结合水声定位技术，基于倒置的超短基线声学基阵，利用平面波近似法推导出应答器相对USBL的定位方法。综合采用INS/USBL组合导航方法，通过卡尔曼滤波器对导航误差进行估计，有效降低了导航参数的误差，抑制了纯惯导误差积累及水下电磁波传播能量衰减问题。考察USBL的原始斜距、斜距差以及声学基阵的空间分布信息并合理建立误差模型，提出一种紧耦合方法以提高系统的动态性能和抗干扰性。仿真结果表明，该耦合方法有效地估计出各导航参数误差，精简了USBL应答器装置数目，降低硬件成本，且相对松组合方法导航精度平均至少提高30%以上，对于进一步提高水下潜航器高精度导航定位，该算法具有重要的工程应用意义和价值。针对考察USBL的斜距、斜距差等原始信息的紧耦合算法，在实际工程应用中，可能会出现水下信号传播时的多径效应，产生斜距量测异常值，在下一部分工作中，应用基于Huber的M估计算法构造伪观测量提高系统鲁棒性及稳定性是迫切并具有实际需求意义。

[1]惠俊英,生雪莉.水下声信道[M].北京:国防工业出版社,1992:1-29.

[2]刘帅.GPS/INS组合导航算法研究与实现[D].解放军信息工程大学,2012.

[3]陈坡.GNSS/INS深组合导航理论与方法研究[D].解放军信息工程大学,2013.

[4]李传军,彭钟锋,李兴城.惯性导航系统自适应辅助GNSS矢量跟踪方法[J].探测与控制学报,2014,36(5):74-79.

[5]张涛,徐晓苏,李瑶.基于惯导及水下声学辅助系统的AUV容错导航技术[J].中国惯性技术学报,2013,21(4):512-516.

[6]张亚文,莫明岗,马小艳,等.一种基于集中滤波的SINS/DVL/USBL水下组合导航算法[J].导航定位与授时,2017,(1):25-31.

[7]Vickery K.Acoustic Positioning Systems.New Concepts-The Future[C]//Proceedings of the 1998 Workshop on Autonomous Underwater Vehicles,AUV’98,Cambridge,1998:103-110.

[8]Jalving B,Gade K,Hage O,et al.A Toolbox of Aiding Techniques for The HUGIN AUV Integrated Inertial Navigation System[C]//Proceedings ofthe OCEANS’03 MTS/IEEE,San Diego,2003:1146-1153.

[9]Morgado M,Oliveria P,Silvestre C.Tightly Coupled Ultra short Baseline and Inertial Navigation System for Underwater Vehicles:An Experimental Validation[J].Journal ofField Robotics,2013,30(1):142-170.

[10]Morgado M,Oliveria P,Silvestre C.Embedded Vehicle Dynamics Aiding for USBL/INS Underwater Navigation System[J].IEEE Transactions on Control Systems Technology,2014,22(1):322-330.

[11]李守军,陶春辉,包更生.基于卡尔曼滤波的INS/USBL水下导航系统模型研究[J].海洋技术,2008,27(3):47-50.

[12]张亚文，莫明岗，马小艳，邓继权.三应答器SINS/USBL紧耦合导航算法[J].导航定位与授时,2015,2(3):29-33.

Research on INS/USBL Integrated Navigation Algorithm Based on the Inverted Acoustic Array

XU Bo,HAO Rui,WANG Chao,ZHANG Xun
College of Automation,Harbin Engineering University,Harbin 150001,Heilongjiang Province,China

This paper aims to address the problems occurred during underwater vehicle navigation,for example,electromagnetic wave is unable to be used as decay underwater,INS has accumulated mass error,and the precision of positioning of underwater vehicles needs to be improved.Based on the inverted acoustic array of Ultra Short Base Line(USBL),this paper thoroughly studies the return transfer time(RTT)of acoustic wave and the approximate method of plane wave.It also derives the positioning method of the transponder with respect to USBL.Combined with the INS error equation,the mathematical model of INS/USBL is established for integrated navigation system.In order to improve the accuracy,dynamic performance and anti-interference performance of the system,the INS/USBL compact combination technique is studied based on the original slant-range of USBL,slant-range difference and the spatial distribution information of acoustic array.The navigation algorithm is verified by MATLAB simulation,and the results show that two kinds of INS/USBL integrated navigation algorithms are able to inhibit filtering divergence of INS to effectively estimate the error angle.Tight combination method is more obvious for reducing the effect of navigation errors.It has more than 30%improvement in relative navigation parameters to loose integrated navigation.Therefore,it is of great significance for the navigation and positioning of underwater vehicles as well as for marine detection.

integrated navigation algorithm;inertial navigation system;Ultra Short Base Line (USBL);tight combination technique

V249.32+8

A

1003-2029（2017）05-0046-09

10.3969/j.issn.1003-2029.2017.05.008

2017-05-31

国家自然科学基金资助项目（61203225，61633008）；黑龙江省自然科学基金资助项目（QC2014C069）；中央高校专项基金资助项目（HEUCF041702）；海洋工程国家重点实验室开放课题（1616）资助

徐博（1982-），男，副教授，主要从事惯性导航、组合导航、初始对准、信息融合研究。E-mail:xubocarter@sina.com

张勋，E-mail:zhangxun_hit@sina.com