橡胶单轴拉伸试验数据处理方法研究
陈小敏
(中石化中原油田分公司天然气处理厂, 河南 濮阳 457162)
橡胶单轴拉伸试验数据处理方法研究
陈小敏
(中石化中原油田分公司天然气处理厂, 河南 濮阳 457162)
针对使用GB/T 528—2009方法对橡胶材料单轴拉伸试验数据处理所得到的材料本构关系误差大的问题,使用橡胶材料本身大变形不可压缩特性的原理,提出了新的处理拉伸试验数据的方法。将GB/T 528和新方法得到的橡胶材料的本构关系导入ABAQUS中进行数值模拟,分别将模拟得到的拉伸伸长量与实验结果进行对比。分析结果表明,采用新方法计算的试样最大拉伸变形量与实验数据的误差为12.57%,采用GB/T 528方法的误差为29.25%。因此大变形不可压缩方法可提高单轴拉伸试验所得到的橡胶本构关系的精度。
橡胶;本构关系;不可压缩;有限元
0 前 言
橡胶材料属于超弹性体,是不可压缩且具有高度非线性的复合材料[1]。橡胶的非线性主要体现在它的应力-应变曲线不呈线性变化,其力学性能和物理属性完全不同于金属材料,属于超弹性材料,具有复杂的本构关系,很难用一种确切的力学模型对橡胶材料进行描述。现在已有多种成熟的理论模型对橡胶本构关系进行描述,其中比较有代表性的有Мooney-Rivlin、Yeoh、Оgden和Gent等本构模型[2]。不同的橡胶应选取对应的本构模型,以确保分析精度。橡胶本构关系的试验方法和试验数据的处理对橡胶的本构关系精度有影响。本研究将从试验数据处理方法上对本构关系精度的影响加以研究。
现在得到橡胶本构关系的方法一般是运用GB/Т 528——2009《硫化橡胶或热塑性橡胶 拉伸应力应变性能的测定》来处理理想橡胶试验数据。但运用该方法得到的本构关系运用到有限元模型分析时有较大的误差,会直接影响到有限元计算所得到结果的精度。本文提出用大变形不可压缩方法来处理拉伸试验时所得到的橡胶材料的试验数据,从而提高橡胶本构关系的精度。
1 单轴拉伸实验
采用封隔器所用的丁腈橡胶为试件,试件的尺寸规格符合GB/Т 528—2009标准之规定,为厚2 mm、宽6 mm、标距25 mm的哑铃I型试件。采用微机控制的电子万能试验机,在常温状态下以450 mm/min的速度进行拉伸,直到拉伸变形量达到190%。共进行了三组试验,将三组试验数据取平均值[3],如表1和图1所示。
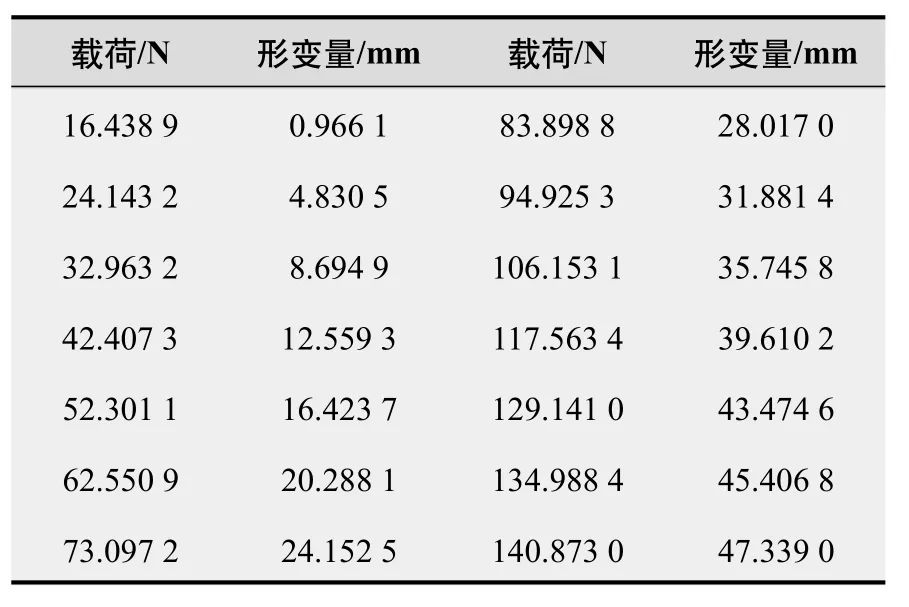
表1 单轴拉伸试验数据

图1 单轴拉伸试验曲线
2 试验数据处理
2.1 GВ/Т 528—2009方法
对试验数据的处理一般采用GB/Т 528—2009中的方法,该方法的基础是基于材料的小变形理论。当材料受到轴向拉伸时,假设试样的横截面积不变或改变很小,可以忽略不计。因此试样受到拉伸时,其压缩应力(σ)和压缩应变(ε)可以根据公式(1)和(2)进行计算[4]:

式中:P为施加在哑铃状试样上的轴向拉伸载荷,S0为试样的原始横截面积,ΔL为试样的轴向拉伸变形量,L0为试样的原始轴向长度。
运用以上两个公式,对表1单轴拉伸试验数据进行处理,得到应力-应变关系,即橡胶本构关系曲线图(图2)。
2.2 大变形不可压缩方法
在哑铃状试样受单轴拉伸的试验中,试样受到的是简单拉伸。简单拉伸的定义为:应变比λ1=λ,λ2=λ3=λ-1/2,如图3所示。
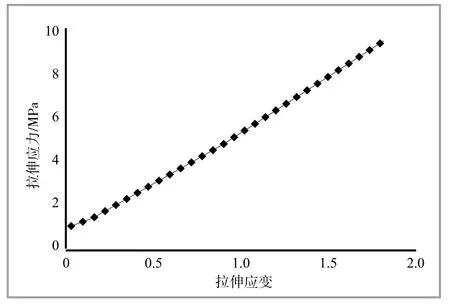
图2 GВ/Т 528方法处理的橡胶本构关系曲线
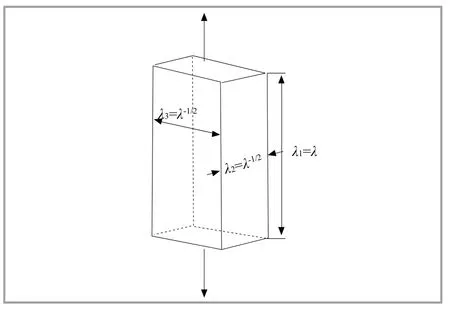
图3 简单拉伸时的主要拉伸比
这种变形满足不可压缩的条件,体积是不变的,因此λ1λ2λ3=1。由于橡胶是各向同性、体积不可压缩的[5],因此,本文中所提到的不可压缩即橡胶在受到简单拉伸或压缩时,其体积保持不变。橡胶在单轴拉伸试验前、后的体积不变,由于哑铃状不规则性和拉伸试验时伸长部分主要是哑铃状试样的中间部分,因此假设试样中间部分在拉伸前、后体积不变,可以表示为:
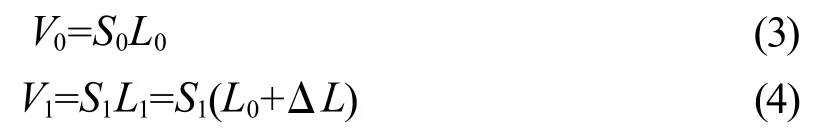
式中:V0和V1分别为拉伸前、后试样中间部分的体积,S0和S1分别为哑铃状试样拉伸变形前、后的中间长方体的横截面积。
根据橡胶试样拉伸前、后体积不变的假定,则V0=V1,将上述两式整理得出拉伸后的横截面积为:

因此,橡胶试样的拉伸应力可表示为:
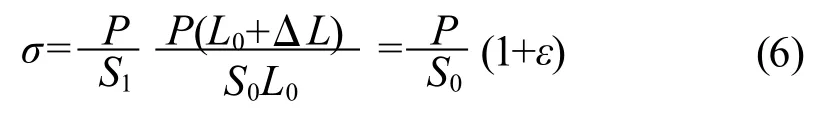
其应变的表达式不变,对表1单轴拉伸试验数据进行处理,得应力-应变关系,即橡胶本构关系曲线图(图4)。
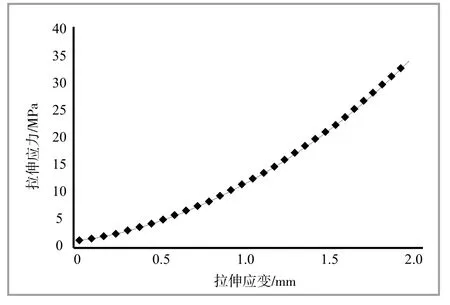
图4 大变形不可压缩方法处理的橡胶本构关系曲线
3 选择本构关系模型
橡胶材料本构关系模型选择的正确与否,直接影响到橡胶产品设计的成功与否,以及结果的可行性。尤其是当采用有限元分析时,本构模型的选择直接影响到计算结果的精度。常用的橡胶本构关系模型有Мooney-Rivlin、Yeoh、Оgden和Gent等模型,一般选用本构模型的方法是运用最小二乘法对本构模型进行优选,对模型进行误差评估和比较[6]。该方法原理复杂,计算繁琐且工作量较大。本研究运用АBАQUS软件材料模块中可以对单轴拉伸、压缩试验数据进行拟合的功能,对试验数据进行拟合,选取与试验数据拟合度较高的本构关系模型[7]。且该材料模块可以对超弹性材料的稳定性进行评价。超弹性材料在变形过程中,从一个平衡状态向另一个平衡状态转变时会产生比较明显的分岔现象。分岔是叙述超弹性材料稳定性问题的核心,橡胶材料在大变形的情况下能否正常工作在很大程度上取决于橡胶材料的稳定性,因此选取橡胶本构模型能否对橡胶的稳定性进行正确的描述也是至关重要的[8-9]。本研究结合试验数据与拟合曲线的重合度,以及本构关系模型对橡胶稳定性的描述来选取合适的本构关系模型。将GB/Т 528方法和大变形不可压缩方法处理的试验数据分别导入软件的材料模块,并与Мooney-Rivlin模型、Yeoh三次幂模型和Оgden四、五、六常数模型进行对比,其中Yeoh三次幂模与试验数据的拟合度较高,且在该本构模型的关系下,材料为稳定的超弹性材料。拟合曲线图如图5和图6所示。

图5 GВ/Т 528方法拟合曲线
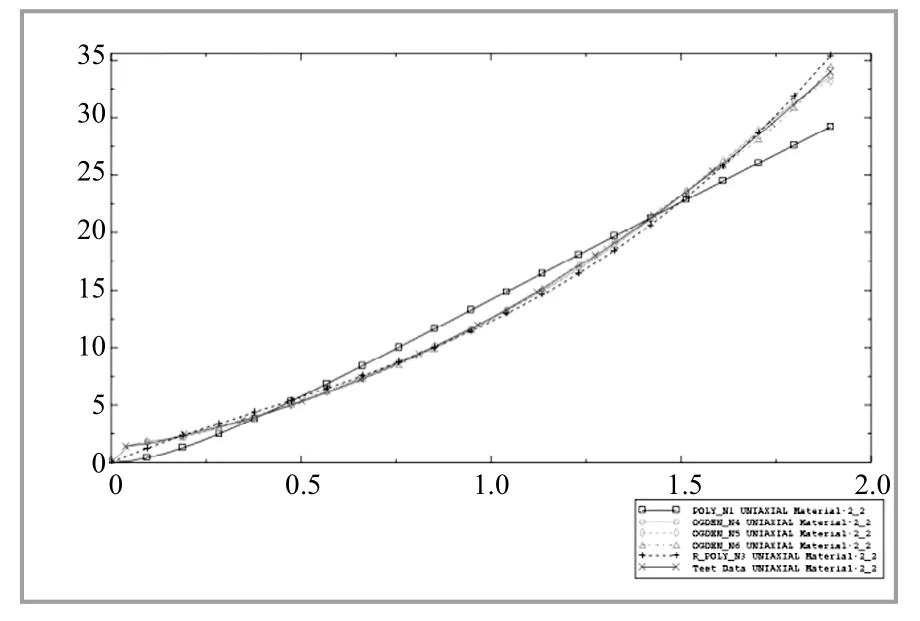
图6 大变形不可压缩方法拟合曲线
4 模拟计算对比
分别将GB/Т 528和大变形不可压缩两种方法处理橡胶单轴拉伸试验数据所得到的本构关系导入АBАQUS软件,进行有限元模拟分析,解算后选取最大拉伸位移变形量与实验测定值的误差作为评价标准,判断两种处理方法的优劣。
根据GB/Т 528中的要求,建立哑铃状试样模型,运用АBАQUS软件模拟单轴拉伸试验。单轴拉伸试验有限元模型如图7所示。
用GB/Т 528方法处理试验原始数据,将得到的本构关系数据导入АBАQUS软件,利用Yeoh模型拟合得:C10=1.896 15,C20=-5.530 8×10-2,C30=9.245 1×10-3。由于是不可压缩材料,泊松比取0.5。模拟得到的橡胶试样最大轴向拉伸位移形变量为68.50 mm(如图8所示)。而单轴压缩试验实测值为47.34 mm,模拟结果偏差为29.25%。
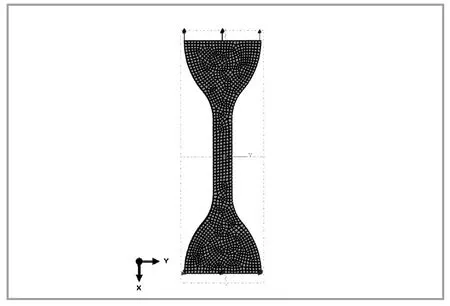
图7 单轴拉伸试验有限元模型

图8 GВ/Т 528方法拉伸试验模拟结果

图9 大变形不可压缩方法拉伸试验模拟结果
用大变形不可压缩方法对试验原始数据进行处理,将得到的本构关系数据导入АBАQUS软件,利用Yeoh模型拟合得到:C10=2.400 5,C20=0.251 0,C30=8.529 5×10-3。模拟得到的橡胶试样最大轴向压缩位移形变量为41.39 mm(如图9所示)。而单轴压缩试验实测值为47.34 mm模拟结果偏差为12.57%。
误差的存在主要是由于橡胶材料在实际情况下具有一定的体积拉伸变形。Yeoh本构模型理论上可能也存在误差以及有限元分析软件带来的误差。这些因素综合影响导致大变形不可压缩方法的模拟计算结果与试验的偏差仍然还有12.57%。
由以上两种情况可知,采用橡胶大变形不可压缩方法处理试验数据所得到的本构关系精度有大幅度的提高。
5 结 论
针对运用GB/Т 528方法处理橡胶单轴拉伸试验数据所得到的本构关系精度较低的问题进行分析,运用橡胶本身大变形不可压缩的特性,提出新的处理试验数据的方法。将GB/Т 528和新方法得到的橡胶材料的本构关系导入АBАQUS中进行数值模拟,分别将模拟得到的拉伸伸长量与实验结果进行对比。对比结果发现,运用GB/Т 528方法的计算误差为29.25%,运用大变形不可压缩方法得到的结果误差为12.57%,即运用大变形不可压缩方法使精度提高了16.68%。因此,使用大变形不可压缩方法对橡胶单轴拉伸试验所得到的数据进行处理可以提高橡胶的本构关系精度,从而提高对橡胶进行有限元分析时的精度。
[1]李晓芳,杨晓翔.橡胶材料的超弹性本构模型[J].弹性体,2005,15(1):50-58.
[2]伍开松,徐大萍,严永发,等.橡胶大变形不可压缩方法试验数据处理[J].橡胶工业,2013,60(7):400-403.
[3]陈小敏. 井下环空防喷器胶筒密封性能研究[D]. 成都:西南石油大学, 2015:15-16.
[4]GB/T 528—2009.硫化橡胶或热塑性橡胶拉伸应力应变性能的测定[S].
[5]詹特 A N(美)主编, 张力群,田明 译. 橡胶工程——如何设计橡胶配件[M].北京:化学工业出版社,2002:45-46.
[6]伍开松,袁新生,张元,等. 合理选择丁腈橡胶胶筒本构模型探讨[J].西南石油大学学报,2007,29(5):141-144.
[7]庄茁,由小川,廖剑晖,等.基于ABAQUS的有限元分析和应用[M].北京:清华大学出版社,2009:219-224.
[8]任九生,程昌钧.超弹性残料的不稳定性研究[J].力学进展,2009,39(5):566-575.
[9]金明,鲍志斌. 超弹性材料稳定性的一种判别方法[J].株洲工学院学报,2005,19(6):10-12.
TQ 330.7+3
B
1671-8232(2017)10-0034-05
陈小敏(1988— ),男,河南范县人,助理工程师,工学硕士。
[责任编辑:朱 胤]
2016-10-14

