我国未来劳动力供给总量及结构预测

田 帆

我国未来劳动力供给总量及结构预测

田 帆

经济的发展离不开劳动力人口的支持，劳动力的供给将直接影响一国经济的正常运行。本文利用人口年龄移算法预测了中国劳动年龄人口总量及年龄构成，再通过回归分析法确定了劳动力供给与各年龄段劳动年龄人口之间的相关系数，从而对劳动力供给总量及年龄结构、未来劳动力供给的性别结构及素质结构进行了预测，并根据实证研究结果，提出了一定的政策启示。

人口总量 劳动力供给总量 劳动力供给结构 年龄移算法 多元回归

一、问题的提出

在国家层面，劳动力作为一种普遍的经济资源或资本，对一个国家发展起着至关重要的作用。人民生活水平的提高是经济发展的根本目的，而经济的发展又离不开劳动力人口的支持，劳动力的供给将直接影响一国经济的正常运行。改革开放以来我国在经济飞速发展取得显著成绩的同时，劳动力市场也逐渐出现了一些新的问题。

第一，劳动力市场供求态势发生了重要变化。“用工荒”问题自2004 年开始在全国范围内蔓延，伴随企业用工成本提升、产业结构调整等问题，企业大批裁员、用工减少等劳动力市场就业问题进一步凸现。第二，人口年龄结构逐渐趋于老龄化。未来我国即将步入人口老龄化社会，届时我国庞大的人口规模将很可能从经济增长的助推器演变为负担。第三，劳动力结构亟待优化。深化改革要求中国转变增长方式，发展知识密集型产业，而这需要优化劳动力市场的结构，提升劳动者素质。

对未来劳动力总量进行测算是应对新形势下各种挑战的重要前提。本文将从人口学视角，以人口年龄结构的变化为基础，对我国未来15年劳动力供给总量及结构变化进行测算，以期为我国宏观经济和人口政策的制定提供参考。

二、文献综述

一个国家劳动力供给数量是人口总量的一部分，而劳动力供给的预测可以理解成人口预测的一个分支领域。因此，迄今为止，国内外不少学者运用统计学、数学、人口学等方法对不同国家及地区的人口进行过预测。总体而言，人口预测方法可以分为以下两类：

第二类是以数学理论为基础的方法。任强基于ARMA模型对我国2010—2050年期间每5年总人口做了预测，预测结果显示我国总人口将在2020年达到历史最大值14.35亿，之后开始下降。*任强、候大道：《人口预测的随机方法：基于Leslie矩阵和ARMA模型》，《人口研究》2011年第35卷(2)，第28～42页。蒋辉采用灰色模型对我国2015—2030年人口做了预测，预测结果显示我国总人口在2015年、2020年、2025年、2030年分别达到13.48亿、13.60亿、13.68亿、13.73亿。*蒋辉：《我国人口预测分析》，《科技管理研究》2005年第11期，第142～145页。易亮用灰色模型对我国未来人口变化的预测结果显示我国总人口在2015年、2020年将达到14.23亿、14.83亿。*易亮：《基于MATLAB的人口预测方法分析》，《价值工程》2012年第9期，第226～227页。董环宇以2000年人口普查数据为基础以5岁为一组预测了我国人口，结论显示我国劳动年龄人口将在2025年达到峰值，以后呈现逐年下降的趋势。*董环宇：《从人口年龄结构变动分析我国未来劳动力供给的变化》，吉林大学硕士学位征文，2009年。

第二类方法相比第一类方法，具有更强的普适性，不仅可以进行人口预测，还可以进行股票、房价等很多其他领域的预测。然而，普适性意味着模型本身并没有考虑人口问题所特有的变化规律。相比较之下，第一类方法将人口作为内生系统进行了更为深入地思考，考虑了现状、出生率、死亡率、迁入迁出率等因素以及这些因素之间的相互关系。就人口预测而言，第一类方法比起第二类方法更为规范，有着更高的期望准确度。

此外，关于劳动力供给的预测，很多学者通过年龄移算的方法预测出了我国未来的劳动年龄人口，但很少有学者对经济活动人口即劳动力供给进行较为严谨的预测。

三、研究设计、基本假设与研究方法*本研究全部数据来源：国家统计局网站，http：//www.stats.gov.cn/.htm，2014-11-01/2014-12-23。

(一)研究设计

由于人口普查年度的人口数据会包括每一岁的人口数量，比起其他年份更为准确详细，因此本研究以第六次人口普查年份的2010年作为基期年份。首先以每一岁为一组通过年龄移算的方法对我国未来各年龄人口进行预测，然后以现有数据为基础求出劳动力供给与劳动年龄人口之间的回归关系，进而预测出我国未来的劳动力供给。预测过程主要分为三个步骤：

第一步，未来劳动年龄人口预测。预测的基本过程是：按照第六次人口普查报告的相关数据，计算基期各年龄人口数；按照各年人口抽样调查数据，预测各年龄人口死亡率和新生人口产生比的平均趋势值；根据人口产生比，计算新一年度0岁新生人口数，结合上年度各年龄人口数，计算新一年度0岁及以上各年龄人口数；计算出新一年度总人口及各年龄人口之后，可以依据新一年度的数据不断计算出更新一年的数据，从而得到及其以后各年的人口预测数据。由于新一年度总人口由各年龄人口组成，依据新一年度0岁新生人口与1岁及以上各年龄人口，可以不断计算新一年度总人口及其各年龄人口数，从而得到基期以后各年的人口预测数据并由此得出各年的劳动年龄人口数据。

第二步，经济活动人口与劳动年龄人口的回归关系。按照各年人口抽样调查数据，以经济活动人口为因变量，各年龄段的劳动年龄人口为自变量，求得经济活动人口与劳动年龄人口之间的回归关系。

第三步，根据前两步的结果，预测未来劳动力供给，同时分析劳动力供给中的年龄、性别及素质结构。

(二)基本假定

国际人口流动影响忽略不计。随着改革开放的深化，国际人口流入和流出对我国人口变化具有一定的影响，但相对我国庞大的人口基数而言影响有限。在本研究中，假定国际人口流入和流出的规模和结构在未来仍保持稳定，即国际人口流动对我国人口总量和结构的影响就可以简单忽略不计。

不考虑宏观政策对人口结构的影响。本研究的立足点是假定现有人口、生育、教育政策保持不变的情况下预测未来劳动力供给总量及结构变化，为未来国家宏观政策制定提供一定启示，因此在研究过程中不考虑政策变化的影响。

不考虑战争、瘟疫等突发事件的影响。战争、瘟疫等突发事件对人口变化的影响是难以预测的，因此本研究不考虑这种突发事件的影响。

(三)研究方法

1.通过ARMA预测各年龄人口死亡率

从我国人口统计的历史经验来看，我国各年龄人口的死亡率虽然有波动，但随着时间推移都呈下降之势，这也是随着科技进步与经济发展造成人类平均寿命不断延长的重要体现。考虑到未来人们生活水平以及现代医疗保健水平将会不断提高，本研究采用1996—2010年各年龄段人口死亡率数据为样本，通过ARMA模型对截止到2040年的各年龄段人口死亡率进行了预测。

如果时间序列yt是它的当期和前期的随机误差项以及前期值的线性函数，即可表示为：

yt=φtyt-1+φ2yt-2+…+φpyt-p+ut-θ1μt-1-θ2μt-1-…-θqμt-q

(1)

则称该时间序列yt是自回归移动平均序列，式(1)为(p，q)阶的自回归移动平均模型，记为ARMA(p，q)。φ1，φ2，...，φp为自回归系数，θ1，θ2，...，θp为移动平均系数，都是模型的待估参数。

显然，AR模型和MA模型都是(1)式的特殊情况，即对于ARMA(p，q)，若阶数q=0，则是自回归模型AR(p)；若阶数p=0，则成为移动平均模型MA(q)。

引入滞后算子B，式(1)可简记为：

φ(B)yt=θ(B)ut

(2)

ARMA(p，q)过程的平稳条件是滞后多项式φ(B)的根均在单位圆外，可逆条件是θ(B)的根都在单位圆外。可以证明，满足以上条件时，ARMA(p，q)模型等价与无穷阶的AR过程或者是无穷阶的MA过程。

2.通过年龄移算法预测新增人口

新增人口是每年存活的新生人口，即0岁人口。这是一个在人口预测中需要进行内生化处理的外生性变量。本研究采用秦中春提出的预测方法，并在该方法的基础之上进行了微调。该方法考虑了处于可生育阶段的人口总数、国家计划生育政策、人口实际出生率和婴幼儿保健水平的内在相关性，将其与处于可生育阶段的主要人口的总数量进行了关联，同时计算了新生人口出生率、新生人口死亡率和新生人口产生比率，在此基础上进行了推算。由于我国20岁以下及超过40岁以后生育小孩的比率很小，因此将20～40岁之间的男女总人口作为可生育人口基数。新生人口出生率就是某年新出生的人口与可生育人口基数的比例。新生人口产生比率是新生人口出生率扣除新生人口死亡率后的余额。对新生人口死亡率，直接采用0岁人口死亡率。历史数据表明我国的新生人口出生比率总的趋势是有所降低但波动较大，考虑到变化趋势对新生人口的影响，我们设定预测期的新生人口出生率为基期以前6年新生人口出生率的平均数。这样，假定基期以后新生人口产生比率不变，新一年度0岁人口由上一年20～40岁人口总数和新生人口产生比率决定。相关计算公式为：

某年新生人口出生率=当年0岁人口(/1-当年0岁人口死亡率)/上一年-20～40岁总人口

基期新生人口出生率=average(基期以前5年新生人口出生率)

基期新生人口死亡率=根据ARMA模型预测的0岁人口死亡率

预测期新生人口产生率=基期新生人口出生率*(1-基期新生人口死亡率)

预测期0岁人口=上一年20～40岁人口数*基期新生人口产生率

预测期1～100岁及以上人口。新一年度某年龄段人口，是上一年度上一年龄段人口减去死亡人口，相关计算公式为：

预测期1～99岁某年龄人口=上一年底一年龄人口*(1-本年该年龄人口死亡率+0.001)

这里预测期本年度100岁及以上人口数由上年99岁到本年度还存活人口和上年度100岁及以上人口到本年度还存活人口两部分共同组成。计算公式为：

预测期100岁及以上人口=(上一年99岁人口+上一年100岁及以上人口)*100岁及以上人口死亡率

3.通过多元回归预测劳动力供给总量

基于经济活动人口是劳动年龄人口的一部分的事实，以及通过观察得出的二者之间的规律，我们设经济活动人口为因变量Y，15～24岁劳动年龄人口、25～54岁劳动年龄人口以及55～64岁劳动年龄人口分别为自变量X1、X2、X3，构建经济活动人口与劳动年龄人口之间的回归方程：

Y=aX1+bX2+cX3+d+ε

(1)

其中a，b，c分别为自变量x1、x2和x3的系数，d为常数项，ε为随机干扰项，又由于经济活动人口是劳动年龄人口的一部分，我们设定a、b、c均小于0，并且d=0。

在国家统计局网站可以得到的以上全部现有数据的最近年份为2003年，因此我们选择2003—2013年数据作为样本，通过eveiws6.0软件对数据进行分析。

时间序列回归分析过程中，为避免出现序列自相关性问题进而影响模型的拟合度，一般要求各变量为同阶单整序列，因此在进行具体回归分析之前，我们首先应对各自变量与因变量进行单位根检验，以确定接下来的分析是否合理。

假定某个时间序列是由某一随机过程生成的，即假定时间序列{Xt}(t=1，2，…)的每一个数值都是从一个概率分布中随机得到，如果Xt满足下列条件：

均值E(Xt)=μ，与时间t无关的常数；

方差Var(Xt)=σ2，与时间t无关的常数；

协方差Cov(XtXt+k)=γk，只与时期间隔k有关，与时间t无关的常数。

则称该随机时间序列是平稳的，而该随机过程是一平稳随机过程。

检验变量是否稳定的过程称为单位根检验，其中最常用的是ADF检验(Augented D ickey-Ful Test)，其检验方法是通过下面三个模型完成的：

(3)

(4)

(5)

t是时间变量，代表了时间序列随时间变化的某种趋势。虚拟假设都是H0：γ=0，即存在一个单位根，模型2与另两模型的差别在于是否包含有常熟项和趋势项。在实际检验时，一般按照模型4，3，2的顺序进行，何时检验拒绝零假设，即原序列不存在单位跟，为平稳序列，何时停止检验，否则就要继续检验，直到检验完模型2为止。

如果一个时间序列经过一次差分变成平稳的，就称原序列是1阶单整序列，记为I(1)。一般地，如果一个时间序列经过d次差分后变成平稳序列，则称原序列是d阶单整序列，记为I(d)。显然，I(0)代表一平稳序列。

四、实证研究

(一)人口总量预测

以第六次人口普查年份的2010年为基期，在保持现行人口政策不变的前提下对中国人口总量进行预测，表1为我国未来总人口及年龄结构预测结果。中国未来总人口将先升后降，未来中国人口峰值约为14.26亿人，峰值出现的时间为2028年(图1)。中国2015年人口约为13.76亿人，2020年约为14.07亿人，2025年约为14.24亿人，2030年约为14.25亿人，2035年约为14.09亿人，2040年约为13.80亿人。

图1 2015—2040年中国总人口预测

表1 2015—2040年中国未来总人口及年龄结构预测

分年龄组的预测结果显示，中国2015—2040年间劳动年龄人口和少年人口均呈现逐步下降之势，其中劳动年龄人口下降趋势更为明显，老年人口呈现逐步上升之势，上升速度明显高于劳动年龄人口和少年人口的下降速度(图2)。从构成上看，2010 年时，劳动年龄人口的比重为74.53%，少年儿童年龄人口的比重为16.6%，老年人口的比重为8.87%。2040时，劳动年龄人口的比重减少为61.0%，少年儿童年龄人口比重减少为12.6%，老年人口增加为37.0%。可见，未来我国将面临劳动年龄人口总量减少，劳动年龄人口占总人口比例减少的局面。

(二)劳动力供给总量及年龄结构预测

劳动年龄人口并不全是劳动力供给，劳动力供给即经济活动人口实际上是劳动年龄人口的一部分，图3描述了2010年分年龄段劳动年龄人口与分年龄段经济活动人口的数量情况。从图3中我们可以发现在25～54岁之间的年龄段，两者的差距很小，并且非常接近，15～24年龄段有大量人口处于上学阶段，而55～64岁年龄的很多人口已经或正在进入退休阶段，因此15～24岁和55～64岁两个年龄段两者的差距相对较大。

图2 2015—2040年中国劳动年龄人口、少年人口及老年人口预测

图3 2010年中国劳动年龄人口与经济活动人口关系

基于经济活动人口是劳动年龄人口的一部分的事实以及通过观察得出的二者之间的规律，我们设经济活动人口为因变量Y，15～24岁劳动年龄人口、25～54岁劳动年龄人口以及55～64岁劳动年龄人口分别为自变量X1、X2、X3，构建经济活动人口与劳动年龄人口之间的回归方程：

Y=aX1+bX2+cX3+d+ε

(6)

其中a，b，c分别为自变量x1、x2和x3的系数，d为常数项，ε为随机干扰项。又由于经济活动人口是劳动年龄人口的一部分，我们设定a、b、c均小于0，并且d=0。

在国家统计局网站可以得到的以上全部现有数据的最近年份为2003年，因此我们选择2003—2013年数据作为样本，通过eveiws6.0软件对(1)式中的a、b、c进行计算，得到如下结果：

模型的R2达到了0.9，X1、X2、X3的t检验值也都超过了5%显著水平下的临界值，通过了t检验，模型总体而言拟合度较好，并由此得出经济活动人口与分年龄段劳动年龄人口之间的回归方程：

Y=0.51X1+0.96X2+0.31X3

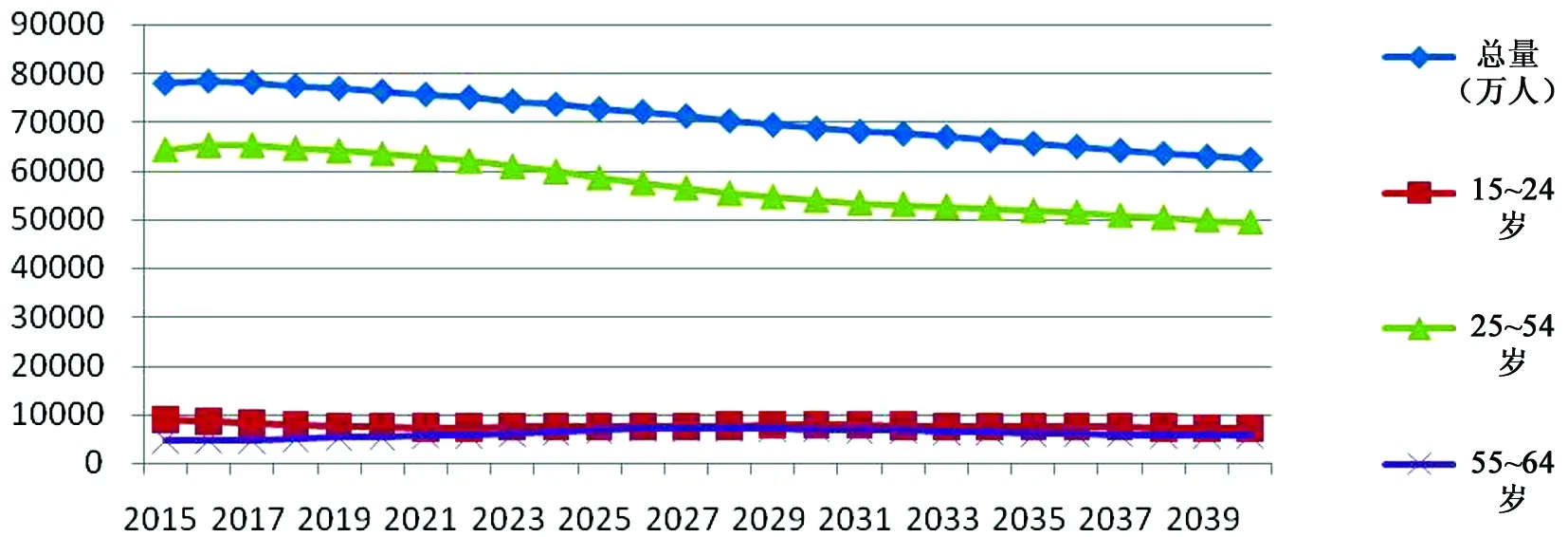
图4 中国2015—2040年劳动年龄人口总量及年龄结构趋势

根据回归方程以及之前分析得到的2015—2040年分年两段劳动年龄人口，我们对2015—2040年间我国劳动力供给情况进行了预测，结果如表2和图4所示。我国劳动力供给总量会在2016年就达到峰值，约为78496万人，随后开始逐年下降。25～54岁年龄段的劳动力供给量变动趋势与劳动力供给总量的变动趋势基本一致，在2016及2017年到达峰值约65226万人，随后开始逐年下降；15～24岁年龄段的劳动力供给量会呈现波动平缓下降的趋势；而55～64岁年龄段的劳动力供给量会先升后降，在2027年达到峰值7308万人，随后开始逐年下降。

表2 中国2015—2040年劳动力供给总量及年龄结构预测结果

(三)未来劳动年龄人口的性别结构预测

相比人口的年龄，人口的性别结构存在着极强的稳定性，有基期数据，只需要考虑死亡率一个因素就可以通过人口的年龄移算法较为轻易地计算出未来15年劳动年龄人口的性别结构，计算结果见图5。未来我国劳动年龄人口中男性人口和女性人口都呈现波动下降之势，同时女性人口的下降速度高于男性，即劳动年龄人口中的男女人口比例在未来将会呈现上升之势。

(四)劳动力供给的素质结构预测

图5 中国2015—2025年劳动年龄人口性别年龄结构趋势

2010年中国第六次人口普查结果显示经济活动人口中未上过学的占3.34%、小学文化程度的占23.44%、初中文化程度的占48.66%，高中文化程度占14.28%、大学专科占6.13%、大学本科占3.75%、研究生占0.38%。可见中国目前的劳动力供给中，初中文化程度的劳动力仍然占了很大一部分，劳动力整体素质依然不高。

根据《教育中长期发展规划纲要(2010—2020年)》的安排，我国在2020年要实现更高水平的普及教育。基本普及学前教育；巩固提高九年义务教育水平；普及高中阶段教育，毛入学率达到90%；高等教育大众化水平进一步提高，毛入学率达到40%；扫除青壮年文盲。新增劳动力平均受教育年限从12.4年提高到13.5年；主要劳动年龄人口平均受教育年限从9.5年提高到11.2年，其中接受高等教育的比例达到20%以上。

虽然根据教育部出台的《全面提高高等教育质量的若干意见》(教高〔2012〕4号)中提出要稳定招生规模，但未来一段时间内本科生教育招生仍然会逐步提高，研究生教育的招生规模即便提升幅度也比较小。随着劳动力供给总量的减少，中国未来本科文化程度劳动力和研究生文化程度劳动力供给总量的比例仍然会逐步提升。

国务院于2014年出台了《关于加快发展现代职业教育的决定》(国发〔2014〕19号)，提出2020年中等职业教育在校生要达到2350万人，专科层次职业教育在校生要达到1480万人。随着高中阶段教育的普及以及职业教育的发展，中国未来高中文化程度劳动力和大学专科文化程度劳动力占劳动力供给总量的比例仍然会逐步提升。

中国目前义务教育普及率已经接近100%，随着义务教育的发展，中国未来未上过学的劳动力将会逐渐消失。由于义务教育普及率已接近100%，而国家在未来要进一步普及高中教育，因此中国未来初中文化程度劳动力占劳动力供给总量的比例会有所下降。

五、结语

(一)本研究的主要结论

第一，我国总人口会在2028年达到峰值14.26亿人，随后开始下降。

第二，我国未来劳动年龄人口和少年人口会逐步下降，而老年人口会逐步上升，同时由于总人口的不断下降，劳动年龄人口占总人口比例会逐渐降低。

第三，我国劳动力供给总量会在2020年之前便达到峰值约7.85亿人，随后会逐年下降，劳动力供给总量占总人口的比重会逐渐降低。

第四，我国未来15年劳动年龄人口中男女比例会进一步提高。

第五，我国未来劳动力供给的平均受教育年限会延长，研究生文化程度、本科生文化程度、大专文化程度、高中文化程度劳动力占劳动力供给总量的比例会有所上升，而初中文化程度和未上过学的劳动力占劳动力供给总量的比例会下降。

(二)政策启示

一是着力构建富有弹性的人力资源市场。宏观层面，要打破城乡、地区、行业、不同所有制之间的劳动力流动和身份转化限制，消除歧视性、限制性规定，构建全国统一的人力资源大市场，促进人力资源高效有序流动。政策方面可积极利用“互联网+”计划，加快建立普惠、互通的就业信息平台，降低工作搜寻成本，减缓摩擦性失业；同时推动创业信息、创业服务、创业孵化有机集成的大平台建设，为创业者和创新型人才提供更多机会和便利。从微观层面，可鼓励用人单位实施弹性工时和差异化工时，通过前者增加有效工作时间，后者为中老年劳动力适当缩短工时和劳动强度、进而为年轻劳动力提供更多进入机会。

二是稳步调整就业年龄上限。对劳动市场人口的年龄进行管制是劳动就业政策的一项重要内容。世界上很多国家对劳动者就业年龄在政策上不设上限，而我国现行政策规定的上限偏低。未来劳动力供给数量及在总人口中所占比例将持续降低，在这种形势下，我们应当调整相关就业政策，给老年劳动力更多选择机会，包括选择继续就业或退休。延迟退休政策的推动应当在满足劳动生产率提升的普遍化和劳动力市场的弹性化、公共政策的家庭化和家庭支持政策的普惠化、养老保险预期权益的清晰化和退休金增长的机制化、社会态度的正面化和涉稳风险的可控化等四个条件的基础上稳步推动，动态调整。

三是进一步构建现代职业教育体系。积极探索本科及以上层次的高等职业教育，打通职业教育中专、大专到职业教育本科以及研究生的上升渠道，实现学历资格证书与职业资格证书等同，打破职业教育学生向上发展的天花板。建立并完善职业教育培训的社会认证体系，为参与不同渠道职业教育的技术工人设计不同的上升渠道，打破社会阶层禁锢，建立通畅的社会垂直流动渠道。按照产教融合、校企合作的发展要求，围绕市场需求对职业教育的专业设置、课程安排、培养模式进行优化与调整，在提升职业教育培训质量的同时，不断强化学生的实践工作能力和技术水平。加大对西部地区职业教育的投入力度，加快发展面向农村地区、民族地区和贫困地区的职业教育。

四是加速实施养老保险制度改革。随着中国社会人口老龄化的不断加速，人口红利也即将转变为人口负债，基本养老基金将面临重大财务危机，因此必须加快养老保险改革速度，弥补养老保险缺口。首先，要合理确定补充保险税收优惠水平，提高企业和个人供款比例；然后，要参考税优商业健康保险试点办法，搭建兼顾保障和增值双重功能的税收延递型养老保险框架，充分激发社会养老储蓄需求。最后，参考美国个人退休账户做法，要探索引入个人养老投资账户，发挥自主投资优势，允许未能参加税收延递养老保险的个人，按照同等税惠比例把部分收入存入专门开设的个人养老投资账户，作为又一个自主储蓄补充保险形式。

(三)研究展望

本研究在取得一定成果的同时，也深深感到了学术水平和研究背景的局限。在以后的研究中，可以在以下两个方面进行深入的分析和拓展。

第一，提高数据的准确性。本文所用数据除人口普查年份外，其余年份的人口年龄结构数据均来自国家统计局每年公布的人口抽样调查结果。人口抽样的结果具有一定的代表性，但比起人口普查数据在准确度上会有一定差距，因此也很可能会在一定程度上造成预测结果的偏差。在将来，随着大数据及统计技术的进步，我们还可以得出更为准确的结果。

第二，死亡率预测的修正。本研究预期各年龄的人口死亡率采取了ARMA模型，虽然短期来看随着人口健康状况的不断改善，人口死亡率的总体趋势一定是下降的，但人口死亡率并不会无限期地不断下降，本研究的预测结果在长期可能会略微偏大。在下一阶段的研究中，可以通过数据预测与专家咨询结合的预测方法对人口死亡率的预测方法进行修正，得出短期长期均适合的预测方法。

1.马歇尔：《经济学原理》，华夏出版社2005年版。

2.西奥多·W·舒尔茨:《人力资本论》，北京经济学院出版社1990年版。

3.陈锡康、杨翠红：《投入产出技术》，科学出版社2011年版。

4.李晖、陈锡康：《基于人口投入产出模型的中国人口结构预测及分析》，《管理评论》2013年第2期。

5.孟令国、李超令、胡广：《基于PDE模型的中国人口结构预测及研究》，《中国人口》2014年第2期。

6.任强、候大道：《人口预测的随机方法：基于Leslie矩阵和ARMA模型》，《人口研究》2011年第35期。

7.蒋辉：《我国人口预测分析》，《科技管理研究》2005年第11期。

8.易亮：《基于MATLAB的人口预测方法分析》，《价值工程》2012年第9期。

9.董环宇：《从人口年龄结构变动分析我国未来劳动力供给的变化》，吉林大学硕士学位论文，2009年。

10.杨雪：《欧盟共同就业政策研究》，中国社会科学出版社2004年版。

11.赵建国：《城市就业问题研究》，高等教育出版社2005年版。

12.蔡昉等：《中国劳动力市场转型与发育》，商务印书局2005年版。

13.曾湘泉：《劳动经济学》复旦大学出版社2010年版。

14.夏杰长：《增长就业与公共政策》，社会科学文献出版社2005年版。

15.Malthus T.An Essay on the Principle of Population.Cambridge：Cambridge University Press，1992.

16.Lewis.On the generational growth of a Population.Biomatrika，1942(06).

17.Leslie P.H.On the use of matrices in certain Population mathematics.Biomatrika，1945(33).

18.Stone R.Demographic Input-output：An Extension of Social Accounting//Contributions to Input-Output Analysis：Fourth International Conference on Input-Output Techniques.North Holland Publishers，Geneva.Switzerland.1970.

田帆，中国宏观经济研究院社会发展研究所助理研究员、管理学博士。

责任编辑：谷 岳