实模态参数的特征曲线法在结构优化设计中的应用

于 澜，耿晓中

(1.长春工程学院理学院； 2.计算机技术与工程学院，长春 130012)

实模态参数的特征曲线法在结构优化设计中的应用

于 澜1，耿晓中2

(1.长春工程学院理学院； 2.计算机技术与工程学院，长春 130012)

提出了实模态参数的特征曲线法及其在结构优化设计中的应用。利用多节点数值技术，绘制实频率、实模态及实频率的一阶灵敏度的曲线，可以有效地避免重频区间、密频区间及模态跳跃区间等不利于结构优化与控制的设计区间，从而寻找设计参数的优化区间，是一种结构优化设计的新方法。一个具有5自由度系统用来展示此方法的有效性及可行性。

实模态参数；灵敏度；特征曲线；结构优化

0 引言

当设计参数取某一数值时，系统的状态可能为重频、单频或密频，而设计参数发生变化时，预测系统的变化状态及程度是非常必要的，例如研究飞机或其他航天器等拥有大量柔性子结构的结构系统时，它们的结构参数很可能因为环境等因素的变化而产生微小变化。本文拟解决的问题：

1)基于较为稳定的数值技术，对设计参数与特征参数的关系进行仿真分析；

2)绘制特征曲线图；

3)分析结构关于设计参数的频率分区，从而确定系统的预期状态，实现振动控制；

4)对其他设计参数重复如上工作，寻找结构相对敏感的设计参数。

如果用的是无阻尼固有频率(也称为实频率或特征值)，就只有实部，那么对应各阶特征值曲线就可以在平面内绘制。如果用的是阻尼固有频率(也称为复频率)，就要用实部和虚数单独绘制[1]。

特征参数取为实模态参数，它包括实频率、阻尼比及实模态(也称为特征向量)，其主要的应用是进行多自由度振动系统的动响应分析。当实频率及实模态能将阻尼矩阵对角化(此时系统称为经典阻尼系统)时，振型迭加法即可实现振动系统的动响应分析(解析解)，若无阻尼固有频率及实模态无法将阻尼矩阵对角化(此时系统称为非经典阻尼系统)时，除了使用直接积分法获得迭代的近似解序列(数值解)，或是近似对角化法，直接略去模态阻尼矩阵的非对角元，使之近似对角化后仍可使用经典阻尼系统的算法近似求解动力响应。最新发展的算法是利用实模态参数并基于频响函数矩阵计算对称系统振动系统响应[2]。事实上除了直接积分法，以上方法均依赖于实模态和实频率能够将质量和刚度矩阵严格对角化，然后重点处理阻尼阵。但从其对角化的证明过程可知，对角化需要两个充分条件，首先是质量和刚度矩阵必须对称，其次是实频率必须各不相同。若在实际应用中遇到非对称或重频系统(实频率重复)，上述方法则不再适用[3-4]。

利用实模态参数还可以求出各自领域的各种灵敏度，对模型修正、结构优化及损伤识别[5]等技术的实现有帮助作用，但同样需甄别上述不同情况。此外，模态跳跃与特征值曲线弯曲[6-7]是由系统模态的快速乃至剧烈变化引起的两种现象。它们的发生表明振动系统关于设计参数的变化是相当敏感的，因此必须关注灵敏度，因为它在很大程度上影响着系统和模态的稳定性[8-9]。这个问题的研究既有理论价值，也对工程实践有着指导意义。密频作为引起这两种现象发生的一个重要因素，也可以由此界定：如果它们之间的差距小到足够引发这两种现象，就可以认为它们是密频。通过比较关键点的导数值可以反映这一点。

从以上分析可知，系统的对称性及重复频率问题对实际工程应用至关重要，否则目前大多数动力分析方法均可能无效，因此，有必要全面考虑设计参数的变化对系统状态的影响。

1 实特征对的灵敏度分析

1.1 实特征分析

对N自由度的线性离散振动系统的运动方程为：

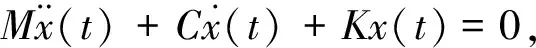
(1)

式中：M，C和K∈RN×N分别为系统的质量、阻尼和刚度矩阵。

(2)

设每个实模态的规范化系数为ai，即

(3)

(K+λiM)φi=0。

(4)

实际上特征方程(4)是关于矩阵M和K的广义特征问题。设φi为规范化实模态，记Φ=[φ1，…，φN]为规范化实模态矩阵，对单频对称系统而言，不同实频率所对应的实模态关于矩阵M和K是加权正交的，且有

ΦTMΦ=E，ΦTKΦ=diag(-λ1，…，-λN)=-Λ。

(5)

实频率λi及实模态φi称为实模态参数。实模态参数在分析系统结构的性能及振动响应等方面起到重要的作用，因此对它们的研究伴随着工程应用的设计、分析、修正、损伤识别等各个方面。

1.2 实特征对的一阶灵敏度分析

对于N自由度的线性离散振动系统(1)，若其在设计、修正和动力分析过程中可以被设计参数向量b=(b1，…，bq)T所描绘，系统的性质矩阵乃至实模态向量均可看成是设计向量的函数，相应地特征方程(4)应为[K(b)+λ(b)M(b)]φ(b)=0，为了讨论方便，以下我们仍记为如式(4)的形式。

文献[10]中给出了实频率的一阶灵敏度

(6)

(7)

其中

(8)

(9)

2 实特征曲线法在结构优化设计中的应用

实特征曲线法是指首先依据结构在设计参数的某取值点处计算其实模态参数及实模态参数的一阶和二阶灵敏度的算法公式，在设计参数的某连续变化的可行域内，利用单点处计算其实模态参数及实模态参数的一阶和二阶灵敏度的离散值，然后用数值方法拟合整个可行域内实模态参数及实模态参数的一阶和二阶灵敏度随设计参数变化而变化的函数曲线，最后根据灵敏度的几何意义及函数曲线的几何性态来分析结构设计中需了解的各种信息，具体操作流程如图1。

下面以一个复杂阻尼结构为例，展示实特征曲线法的基本思路、步骤和分析方法。考虑一个5自由度的质量弹性阻尼系统，设只在垂直方向上产生振动，如图2所示。

图1 实特征曲线法在结构设计优化中的应用操作流程图

图2 5自由度非比例阻尼系统

系统质量阵的元素为：m11=m1;m22=m2;m33=m3;m44=J4;m55=J5;mij=0(i≠j)。

阻尼矩阵的元素与刚度矩阵的元素有类似的形式。例如：c11=c1;c12=-c1;c13=c14=c15=0;c22=c1+c2，等等。

令k3=1 000，其余参数取为m1=200 kg，m2=500 kg，m3=1 000 kg;k1=10 000 N/m，k2=20 000 N/m，k4=k6= 1 000 N/m;c1=4 Ns/m，c2=6 Ns/m，c3=c4=c5=c6=40 Ns/m，取设计参数为k5，960～1 040 N/m，由公式(4)每隔10 N/m采样实频率数据，输出特征值函数曲线图，如图3。

(a)

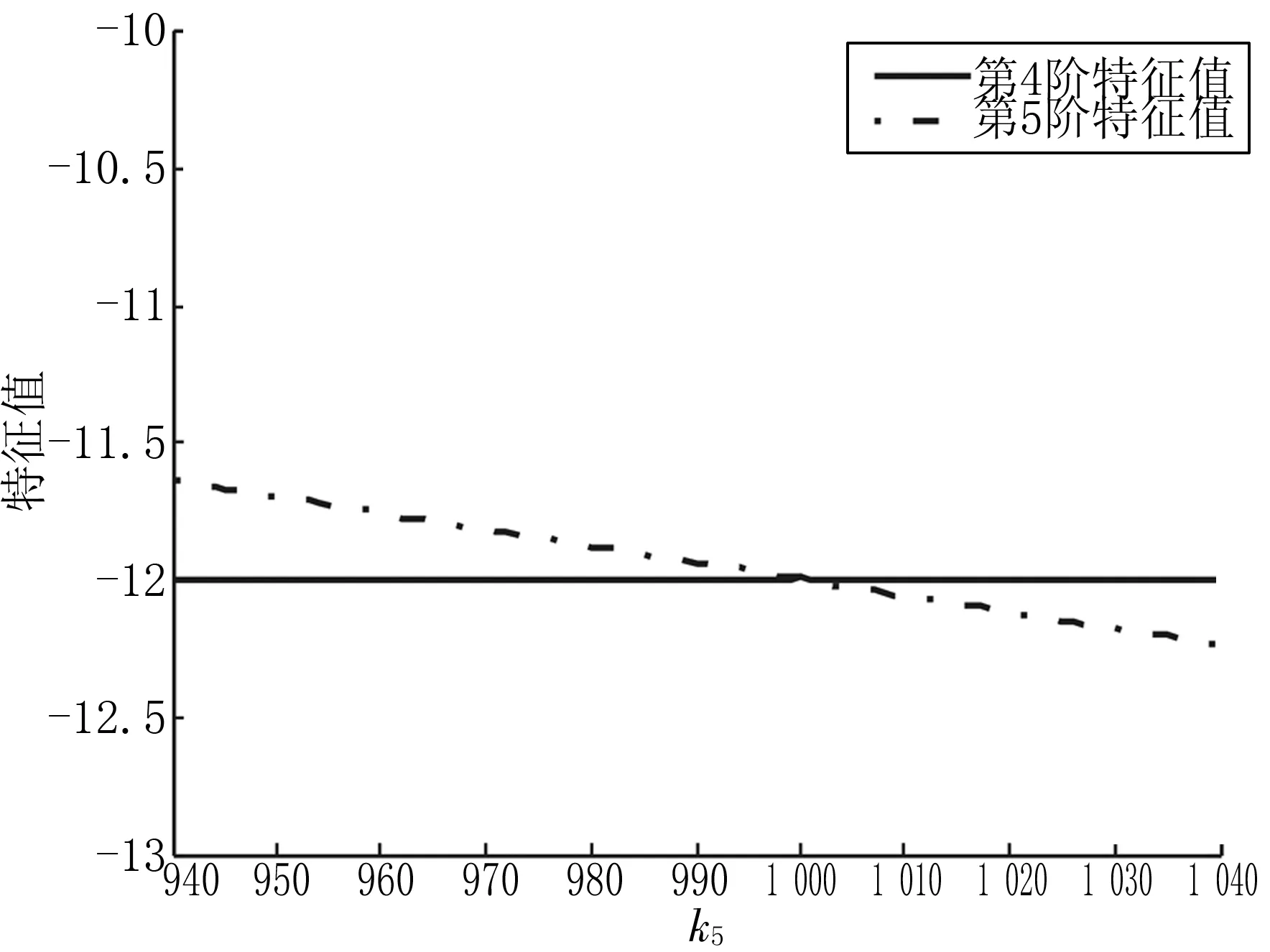
(b)图3 实频率关于设计参数k5的曲线

由图3可知，当设计参数k5从940变化到1 040的范围内，第1，2和3阶特征值始终分区良好，第4阶和第5阶特征值都非常接近，为密频特征值，尤其在设计参数k5=1 000时，这两个特征值相同λ4=λ5=-12，系统处于重频状态。再根据公式(6)计算各节点处的实频率的一阶灵敏度数值，并输出特征值的一阶灵敏度函数曲线图，如图4。

(a)第1～3阶特征值一阶灵敏度函数曲线图

(b)第4～5阶特征值一阶灵敏度函数曲线图图4 实频率的一阶灵敏度函数曲线图

由图4(a)可见，第1、2和3阶特征值的一阶灵敏度的数量级为×10-4，说明灵敏度接近于0，这与图4(a)中的特征值函数曲线的几何性态相符。由图4(b)可见，第4阶和第5阶特征值的一阶灵敏度的数值(除了节点k5=1 000外)，均能正确反映图3(b)中的特征值函数曲线的几何性态，但在节点k5=1 000处，由于此时系统处于重频状态，并不适用公式(6)来计算实频率的一阶灵敏度，强行用公式(6)计算出来的灵敏度并不正确，也确实不能与图3(b)中在该节点处的特征值的变化规律相符合。下面来分析系统当设计参数k5从940变化到1 040的范围时，各阶实模态的变化规律。由公式(4)每隔10 N/m采样各阶实模态数据，输出各阶特征向量函数曲线图，如图5～9。

由图5～9可见除了第3阶实模态，其余各阶实模态均在设计参数k5=1 000时发生了跳跃，而前文已经指出在k5=1 000时系统正处于重频状态。因此为了避免发生结构的稳定性问题，在设计之初就应选取远离重频及密频的设计区间。

图5 第1阶实模态φ1关于设计参数k5的曲线

图6 第2阶实模态φ2关于设计参数k5的曲线

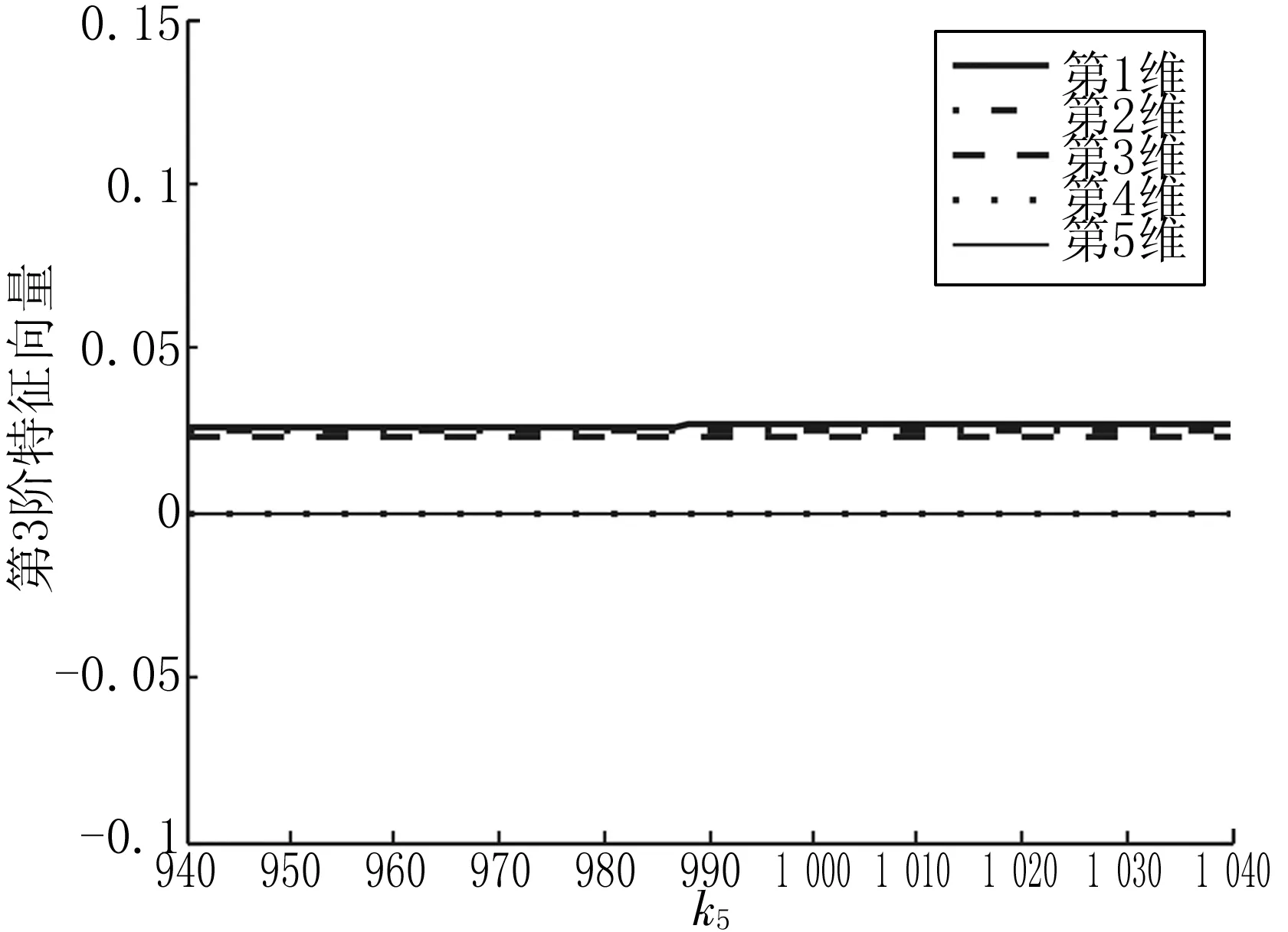
图7 第1阶实模态φ3关于设计参数k5的曲线

图8 第4阶实模态φ4关于设计参数k5的曲线

图9 第5阶实模态φ5关于设计参数k5的曲线

3 结语

1)由特征值函数曲线图可以发现在设计参数k5∈[990，1 010]时，第4阶和第5阶实频率是密集的，这是一个密频区间，而k5=1 000时，第4阶和第5阶实频率相同，此时系统处于重频状态。

2)由特征向量函数曲线图可以发现，在设计参数的密频区间[990，1 010]内，多数实模态都发生了跳跃，而k5=1 000很可能是一个不可导点。

3)特征值的一阶灵敏度曲线及特征向量的一阶灵敏度曲线印证了在该设计区间内的特征值及特征向量函数曲线几何特性。

4)结构优化后设计区间为[940，990]∪[1 010，1 040]。

[1] 于澜，张淼.复模态参数的特征曲线法及其应用研究[J].长春工程学院学报：自然科学版，2017，18(1)：113-118.

[2] 张淼，于澜，鞠伟.基于频响函数矩阵计算阻尼系统动力响应的新方法[J].振动与冲击，2014，33(4)：161-166.

[3] 张淼，于澜.对称经典阻尼系统动力响应精确算法的比较研究[J].吉林师范大学学报：自然科学版，2015，36(1)：99-103.

[4] 张淼，于澜.对称非经典阻尼系统动力响应精确算法比较[J].长春工业大学学报，2015，36(1)：107-110.

[5] 于澜，张任，乐明峰，等.模态参数的灵敏度分析在结构工程领域中的应用[J].长春工程学院学报：自然科学版，2012，13(3)：1-3.

[6] 张淼.数值技术在结构特征值分析中的应用研究[J].长春理工大学学报：自然科学版，2014，37(2)：124-127.

[7] 张淼.密频结构实模态参数的特征曲线法[J].长春师范大学学报：自然科学版，2014，33(2)：1-4.

[8] 张淼，于澜，鞠伟.基于松驰技术的重频密频结构模态灵敏度分析[J].合肥工业大学学报：自然科学版，2012，35(12)：1605-1609.

[9] 张淼，于澜，鞠伟.模态跳跃现象对振动分析的影响[J].合肥工业大学学报：自然科学版，2015，38(11)：1524-1529.

[10] 张淼，鞠伟.计算各种振系模态灵敏度的统一算法[J].长春工程学院学报：自然科学版，2012，13(4)：119-122.

TheApplicationofRealModalParameterEigen-curveinStructuralOptimization

YU Lan，et al.

(SchoolofScience，ChangchunInstituteofTechnology，Changchun130012，China)

The method of real modal parameter eigen-curve is presented in this paper，and its application in structural optimization is also provided.By using the numerical technique，the curves of real rate，real mode，and the real rate first-order sensitivity curve have been drawn to effectively avoid the design intervals which are not conducive to structural optimization and control such as the multiple-frequency interval，closed-frequency interval and jumping interval of mode，and so on.Hereby，the optimization interval of design parameter can be obtained as a new method for structural optimization design.A 5 degree-of-freedom structure system can be used to demonstrate the efficiency and feasibility of this method proposed in this paper.

real modal parameter；sensitivity；eigen-curve；structural optimization

10.3969/j.issn.1009-8984.2017.03.029

2017-06-05

吉林省科技发展计划项目(20160101277JC)吉林省教育厅“十二五”科学技术研究项目(2015306)长春工程学院基金项目(320150018)

于澜(1971-)，女(汉)，吉林永吉，硕士，副教授 主要研究计算力学与结构优化设计。

O32

A

1009-8984(2017)03-0124-05