薄钢板剪力墙等效拉杆模型研究

孙永亮

(陕西国润置业有限公司，陕西 咸阳 712000)

薄钢板剪力墙等效拉杆模型研究

孙永亮

(陕西国润置业有限公司，陕西 咸阳 712000)

首先，对薄钢板剪力墙简化分析模型进行研究，采用通用有限元软件Abaqus建立薄钢板剪力墙Shell单元模型以及采用SAP2000建立等效拉杆简化分析模型，对比两种模型在静力荷载下的力学性能，从而得到等效拉杆模型杆元根数的合理范围。其次，修正了薄钢板剪力墙简化分析模型中杆元面积计算公式，更好地模拟薄钢板剪力墙的初始抗侧刚度。最后，对比等效双向拉杆模型与Shell单元模型两种模型的滞回性能，结果表明：采用SAP2000建立的等效双向拉杆简化分析模型能够较好地模拟出薄钢板剪力墙的滞回性能。

钢板剪力墙；Shell单元模型；等效拉杆模型；有限元分析；滞回性能

0 引言

薄钢板剪力墙是由内填薄钢板、框架梁和框架柱组成的抗侧力结构，具有承载能力高、耗能能力强、延性好等优点，可以有效地提高结构的抗震性能[1]。薄钢板剪力墙在水平往复荷载作用下沿对角线方向形成斜向拉力带，此时钢板剪力墙的承载能力未下降并且具有良好的延性[2]。带有薄钢板剪力墙的结构体系，采用Shell单元模拟钢板剪力墙时计算过于复杂，分析程序不易收敛，导致无法高效、便捷地获得结构整体受力性能。国内外学者对薄钢板剪力墙的简化分析模型进行了广泛的研究与分析。薄钢板剪力墙的简化模型——等效拉杆模型[3](strip model)，如图1所示，模型中采用一系列倾角相同的拉杆代替薄钢板剪力墙承受水平作用时形成的拉力带，并忽略钢板墙的承压能力，拉杆两端与周边框架铰接。目前加拿大规范(CAN/CSA S16.1-94)[4]和美国规范(ANSI/AISC 360-05)[5]推荐采用等效拉杆模型模拟薄钢板剪力墙屈曲后的受力性能。

国内外学者对等效拉杆模型的适用条件进行了分析研究，1983年加拿大学者Timler和kular[6]提出了等效拉杆模型倾角的计算公式：

图1 等效拉杆模型

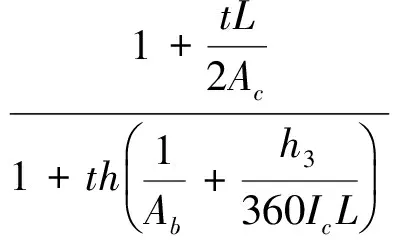
(1)

式中：Ac、Ic为截面面积和惯性矩；Ab为梁截面面积；α为斜拉杆与竖向轴线的夹角；t为内嵌钢板厚度；h为层高；L为墙宽。文献[7-8]对薄钢板高厚比λ、斜拉杆倾角α对等效拉杆模型的影响进行了研究，认为等效拉杆模型适用于分析高厚比λ>300的薄钢板剪力墙，倾角α的变化对钢板剪力墙简化分析模型的影响可以忽略不计，可取α=45°。为确保钢板剪力墙屈曲后形成的拉力带充分发展，框架柱的抗弯刚度须满足：

(2)

以往研究中未给出拉杆根数的合理取值范围。本文基于前人的研究成果，采用SAP2000建立不同杆元根数的等效拉杆模型，并采用通用有限元软件Abaqus建立薄钢板剪力墙壳单元模型。在静力作用下，对比两种模型的屈服位移、极限荷载、初始刚度，得到等效拉杆模型拉杆根数的合理取值范围。修正钢板剪力墙简化分析模型中杆元面积计算公式，更好地模拟了薄钢板剪力墙的初始抗侧刚度。

1 等效拉杆模型静力性能分析

1.1 有限元模型的建立

建立双层单跨薄钢板剪力墙有限元模型，模型总体尺寸如图2所示，模型的构件截面尺寸见表1。其中框架柱的抗弯刚度Ic=1.408×108mm4>Icmin=1.226×107mm4，满足框架柱抗弯刚度的要求。框架梁的抗弯刚度Ib=2.631×108mm4，可认为框架梁的抗弯刚度足够大，可忽略由于框架梁的弯曲作用所产生的附加弯矩。

图2 钢板剪力墙有限元模型基本尺寸

表1 构件截面尺寸 单位：mm

模型中钢板剪力墙尺寸为1 100 mm×1 100 mm，钢板厚度为3 mm，板件宽厚比为λ=367，满足简化分析模型对钢板剪力墙宽厚比的要求。除内嵌钢板材质为Q235外，模型其余部分材质均为Q345，以满足“强框架、弱墙板”的概念设计。钢材采用理想弹塑性本构模型，基本参数见表2。

表2 材料性能参数

采用Abaqus建立薄钢板剪力墙Shell单元模型，如图3所示，其中框架梁、柱采用八节点六面体(C3D8)单元进行模拟，薄钢板墙采用Shell单元(S4R)模拟。框架梁、柱与薄钢板墙均采用绑定(tie)连接，以模拟实际工程中的焊接。加载方式采用位移控制，柱顶位移取60 mm(根据JGJ 99—98《高层民用钢结构技术规程》[9]中规定，取层间位移角L/50)。提取有限元模型中的底部剪力与柱顶位移曲线。

图3 Abaqus有限元模型

采用SAP2000建立薄钢板剪力墙等效拉杆模型，如图4所示，采用pushover静力弹塑性分析，采用SAP2000中默认的塑性铰属性。在每个斜拉杆中间位置定义一个P铰，在柱子的柱顶和柱脚定义P-M-M相关铰，在梁的两端和中点定义主轴方向的弯矩M铰。柱脚支座为固定支座，为了模拟底部全部固定，底部施加节点束缚，将节点6个方向自由度全部束缚，为了约束横梁平面外变形，在梁上节点施加束缚，将Z轴方向的位移束缚，斜拉杆两端铰接，采用释放端部约束来实现[10]。

图4 SAP2000等效拉杆模型

1.2 拉杆根数对简化分析模型的影响

薄钢板剪力墙简化分析模型中，板条宽度等于拉杆之间的间距，每根拉杆的面积等于板条的宽度与板厚的乘积，每根拉杆的截面面积公式如式(3)所示[11]，建立6个等效拉杆模型，其中斜拉杆个数分别为5、11、16、21、26、31根。采用公式(3)计算等效拉杆模型不同杆元根数下对应的截面面积和直径数值见表3。

表3 简化分析模型中不同拉杆数对应的杆截面面积与直径

注：SM-5表示等效拉杆模型采用的拉杆个数为5根，其他类同。

(3)

式中：l、h为内嵌板的宽度和高度；t为内嵌板的厚度；n为每块剪力墙的拉杆个数。

Abaqus有限元模型与SAP2000建立的等效拉杆模型所提取的底部剪力与柱顶位移曲线如图5所示。从图中可以看出，拉杆个数为16、21根时，曲线吻合得很好，极限荷载误差分别为1.79%与1.23%，屈服位移误差为5.1%和7.8%；当根数小于15根或大于21根时，两条曲线相差较大，因此等效拉杆模型的拉杆根数选取具有边界效应，拉杆根数宜取15～20根为宜。两种模型得到的初始抗侧刚度具体数值见表4。其中，拉杆根数在16和21根时，初始抗侧刚度误差分别为25.6%和20.7%，两种模型得到的初始抗侧刚度存在差别的原因是：等效拉杆模型中钢板剪力墙被离散为一系列拉杆，忽略了钢板墙的整体效应，拉杆之间缺乏相互之间的“咬合”，同时忽略了钢板剪力墙对柱抗弯刚度的提高。

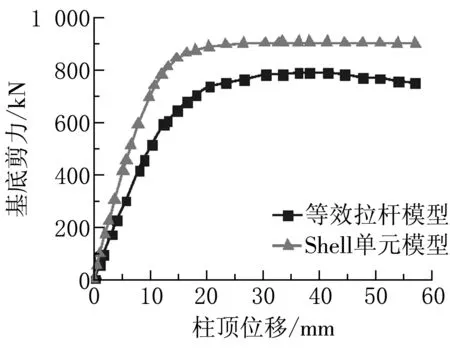
(a)SM-5

(b)SM-11

(c)SM-16

(d)SM-21

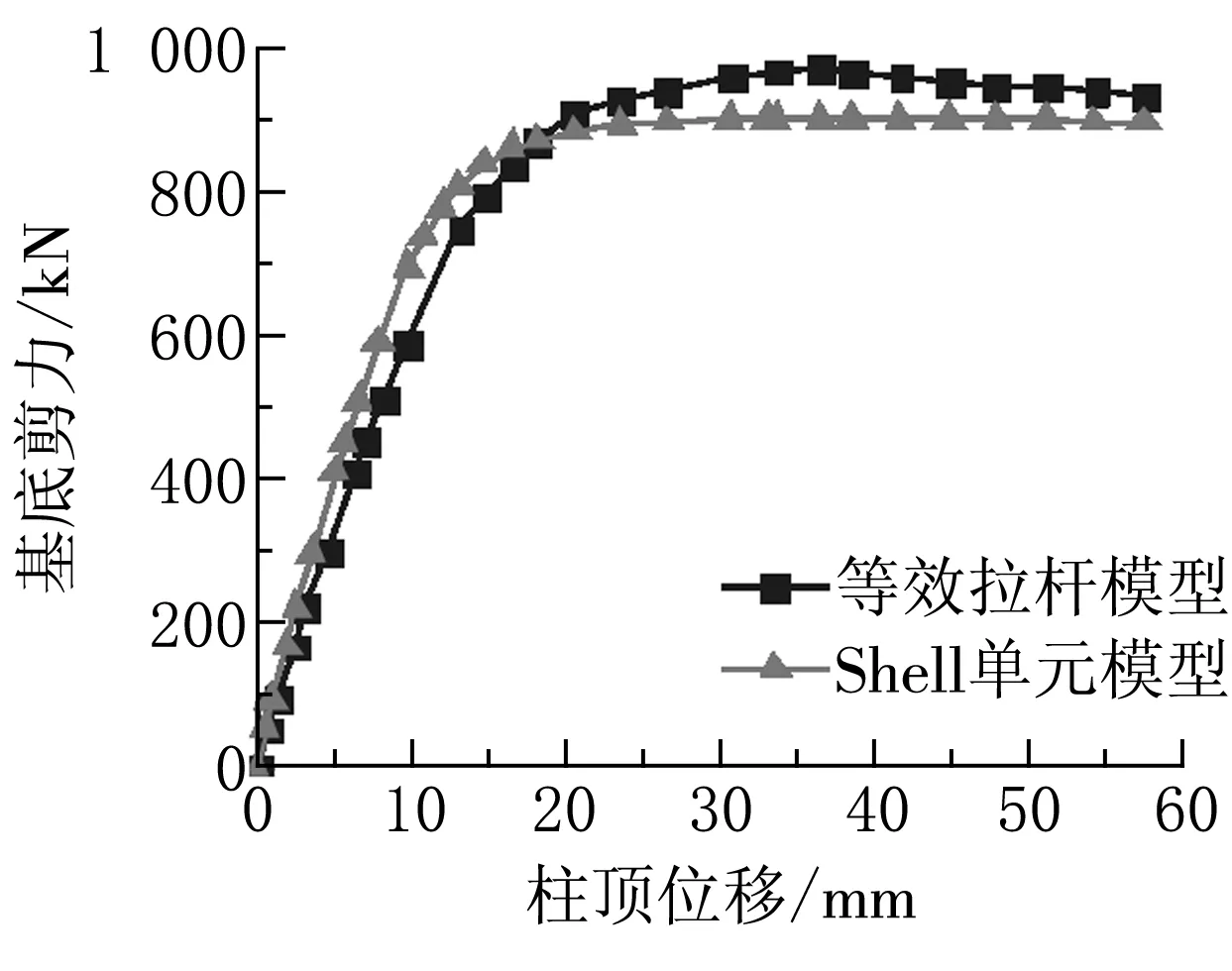
(e)SM-26

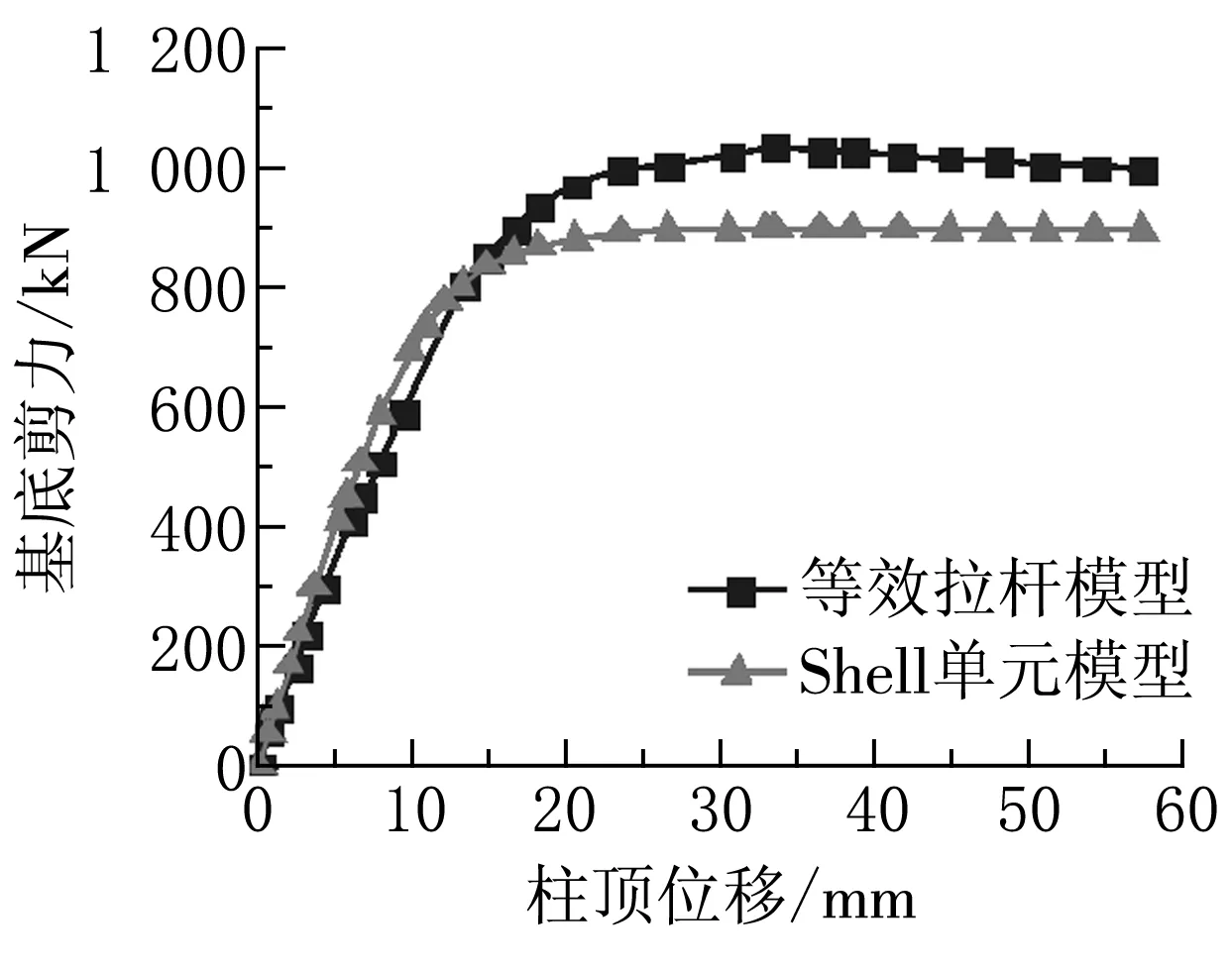
(f)SM-31

表4 不同杆元根数等效拉杆模型数据分析

1.3 杆元面积对简化分析模型的影响

由于等效拉杆模型中忽略了薄钢板剪力墙的整体工作效应，所得到的初始抗侧刚度与实际钢板剪力墙的刚度相差较大。因此，在适合的拉杆根数下(取为16根)，采用修正后的杆元截面积计算公式：

(4)

式中f表示杆元截面积增加系数，f≥1。

增加拉杆的截面积更精确地模拟实际钢板墙的初始刚度，采用公式(4)重新计算拉杆截面积，建立6个等效拉杆模型，其中增加系数f取1.0、1.1、1.2、1.3、1.4、1.5。对应的拉杆截面面积与拉杆直径具体数值见表5。

表5 杆元截面积随增加系数f变化

注:等效拉杆模型拉杆根数取16根。

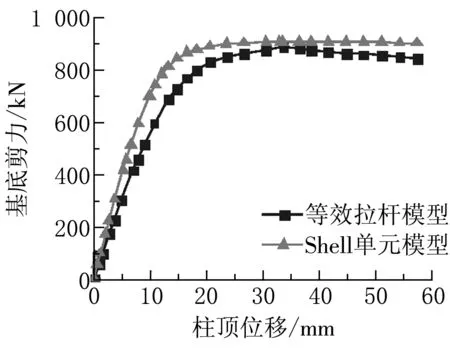
Shell单元模型与修正后的等效拉杆模型提取的底部剪力与柱顶位移曲线如图6所示，从图中可以看出，修正后的拉杆模型的初始抗侧刚度与Shell单元模型的抗侧刚度数值相接近，具体数据见表6，在f=1.2时，等效拉杆模型的初始刚度误差只有13.28%，且屈服位移与屈服荷载误差较小，当f=1.5时，由于拉杆截面积增加太大，导致初始刚度大于Shell单元模型的初始刚度，且对应的极限荷载有很大提高。故增大系数f可取1.2。等效拉杆模型拉杆个数取15～20根，采用修正后的杆元截面积计算公式可很好地模拟实际钢板剪力墙的实际受力性能。

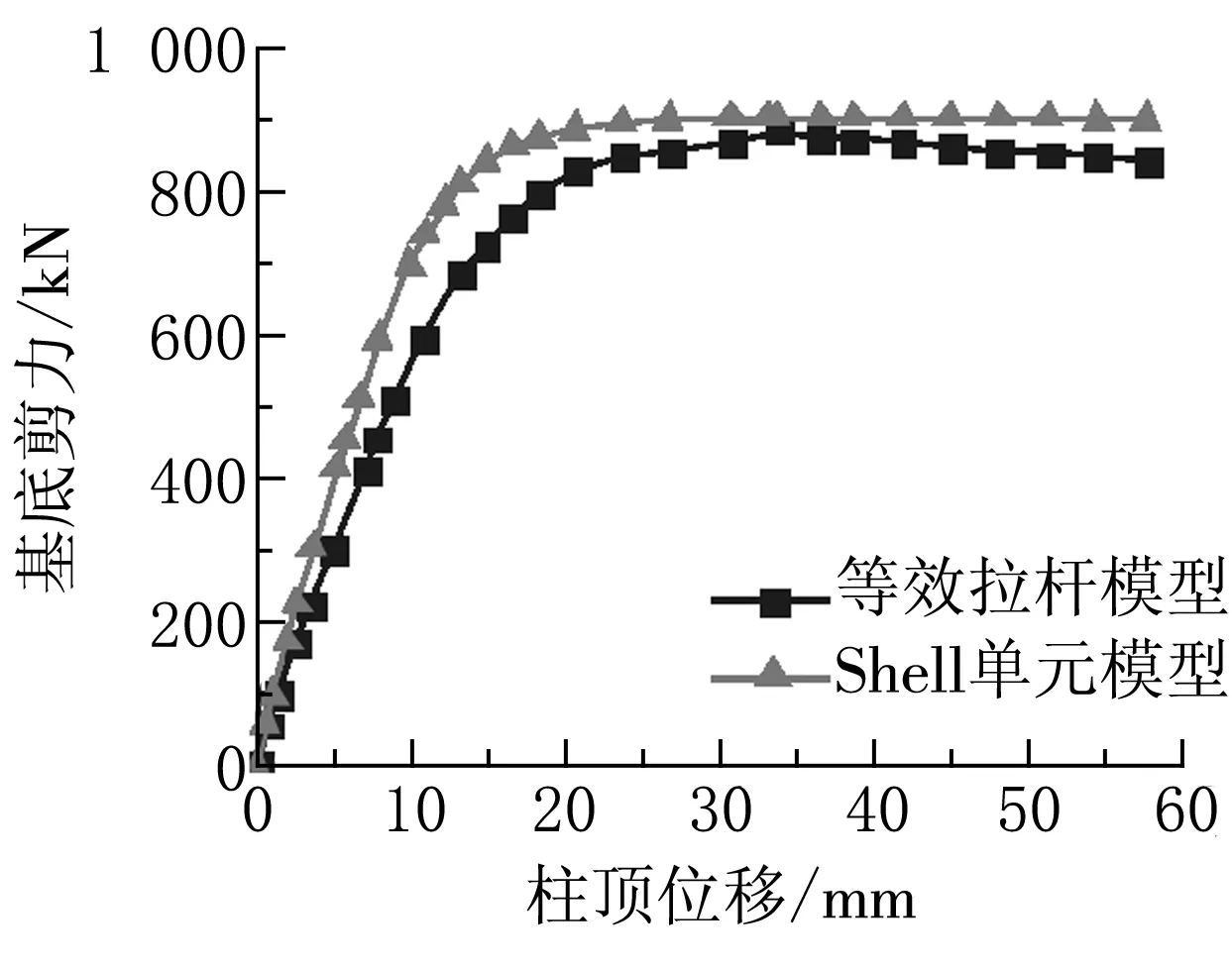
(a)f=1.0

(b)f=1.1

(c)f=1.2

(d)f=1.3

(e)f=1.4

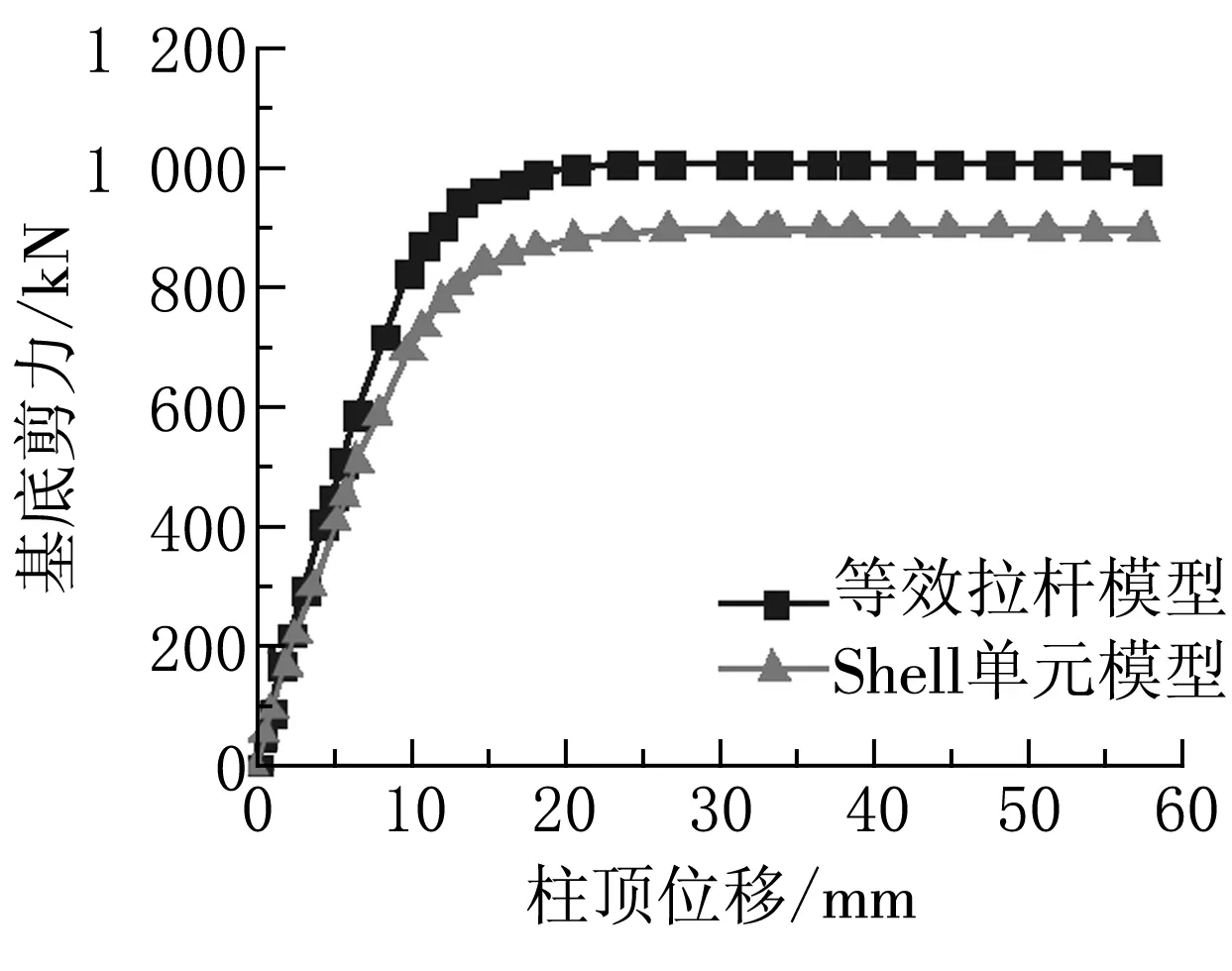
(f)f=1.5图6 Shell单元模型与SM模型曲线对比

2 等效双向拉杆模型滞回性能分析

2.1 等效双向拉杆模型建立

在水平往复荷载作用下，薄钢板剪力墙结构的等效拉杆简化模型需要布置两方向拉杆来模拟钢板剪力墙的受力性能。如图7所示，双向等效拉杆模型在受力时只有相同方向的拉杆参与受力，且只能承受拉力。为简化分析，钢材采用理想弹塑性本构模型。采用Abaqus建立薄钢板剪力墙壳单元模型，采用SAP2000建立双向等效拉杆简化分析模型，对应两种模型在水平往复荷载作用下的滞回性能。

表6 不同增大系数f对应有限元模型初始抗侧刚度数据分析

图7 等效拉杆(双向)模型

2.2 等效拉杆滞回性能验证

从结构的荷载—位移滞回曲线中可以得到结构承载能力、变形能力、耗能能力等重要抗震性能是评价结构抗震性能的重要指标。通过Abaqus建立的Shell单元模型与SAP2000建立的双向等效拉杆模型，对比两种模型的滞回曲线以及其他抗震性能指标，验证双向等效拉杆模型模拟钢板剪力墙抗震性能的有效性。其中，双向等效拉杆模型中拉杆个数取16，杆元截面积采用修正后的计算公式，两种模型均以±10 mm、±15 mm、±20 mm、±25 mm、±30 mm、±35 mm、±40 mm为控制位移进行加载。

图8为Shell单元模型与等效拉杆模型滞回曲线的对比结果，其中实线为Shell单元的计算结果，虚线为等效双向拉杆模型的计算结果。由图8可见，壳单元模型的初始抗侧刚度大于双向等效拉杆模型，两种模型的滞回环所包围的面积较为接近。此外，两种模型计算得到的极限承载力、延性系数和耗能比等指标均吻合很好。另外，模型滞回曲线在加载后期的抗侧刚度退化较大，主要因为框架梁柱刚接，对钢板剪力墙的刚度有提高作用，随着加载位移值的增大，柱腹板、翼缘出现局部屈曲，柱刚度降低，以致钢板墙的整体刚度下降。通过应用等效双向拉杆模型可以高效获得薄钢板剪力墙的各项抗震指标，也为结构体系分析提供一种很好的模型。

图8 Shell单元模型与拉杆模型曲线对比

3 结语

薄钢板剪力墙受力屈曲后形成斜向拉力带，仍具有较高的承载能力，良好的延性与耗能能力，是一种优越的抗侧力构件。薄钢板剪力墙的等效拉杆模型改善了以往采用Shell单元模型模拟钢板剪力墙所带来的收敛、耗时等问题。本文通过建立薄钢板剪力墙Shell单元模型和等效拉杆模型，对比两种模型的静力性能、滞回性能，得到以下结论：

1)等效拉杆模型拉杆根数宜取15～20根；

2)修正的拉杆截面积计算公式中，截面积增大系数取f=1.2时，等效拉杆模型的初始抗侧刚度与薄钢板剪力墙吻合很好，对应两者的极限承载力误差较小；

3)等效双向拉杆模型可以较好的模拟薄钢板剪力墙的滞回性能，利用等效双向拉杆模型可以得到薄钢板剪力墙的各项抗震性能指标；

4)本文研究的等效拉杆模型忽略了薄钢板剪力墙的承压能力，且梁柱刚接，较高的估计了薄钢板剪力墙的承载能力，在今后的研究中可以考虑包含受压杆元的等效拉压杆模型，以模拟出实际薄钢板剪力墙的整体受力性能。

[1] Lubell A,Prion H,Ventura C.Unstiffened steel plateshear wall performance under cyclic loading [J].Journal of Structural Engineering,2000,126(4):453-460.

[2] 陈国栋,郭彦林.钢板剪力墙低周反复荷载试验研究[J].建筑结构学报,2004,25(2):19-38.

[3] Thorburn L J,Kulak G L,Montgomery C J.Analysis of steel plate shear walls[C]//4th International Conference on Steel & Composite Structures.Edmonton:Deparment of Civil Engineering,University of Alberta,1983.

[4] CAN/CSA-S16-01 limit state design of steel structural[S].Canadian standard Association,Toronto,Ontario,1994.

[5] ANSI/AISC 341-05 Seismic provisions for structural steel building[S].Chicago:American Institute of Steel Construction,2005.

[6] Timler P A,Kula G L.Experimental study of steel plate shear walls[J].Minnesota Medicine,1983,69(5):268-270.

[7] 陈国林,郭彦林.钢板剪力墙低周反复荷载试验研究[J].建筑结构学报,2004,25(2):19-38.

[8] 李然，张素梅，马欣伯，等.钢板剪力墙等效拉杆模型的有限元分析[C]//第六届全国土木工程研究生论坛论文集,北京：清华大学，2008.

[9] JGJ99—98高层民用钢结构技术规程[S].北京：中国建筑工业出版社，1998.

[10] 李峰.钢板剪力墙抗震性能的试验与理论研究[D].西安:西安建筑科技大学，2011.

[11] 李峰，吴冠男，李慎，等.十字加劲钢板墙的简化模型[J].西安建筑科技大学学报，2013，45(2)：178-184.

TheStudyontheEquivalentRodModelofThinSteelPlateShearWall

SUN Yong-liang

(ShaanxiNationalResourcesPropertyCo.LTD,XianyangShaanxi712000,China)

Firstly,the study on thin steel plate shear wall simplified analysis model has been made in this paper.The general finite element software Abaqus is adopted to establish the thin steel plate shear wall shell unit model,and equivalent rod simplified analysis model established by using SAP2000 is also adopted.The two kinds of models are compared in mechanical properties under static load,so as to get the reasonable range to root number of equivalent rod model.Secondly,the calculation formula of the pole area in the simplified analysis model of thin steel plate shear wall is corrected,and the initial anti-lateral stiffness of the shear wall of the thin steel plate is better simulated.Finally,the hysteresis performance of the equivalent bidirectional pull rod model is compared with that of shell element model model.The result shows that the equivalent bidirectional pull rod simplified analysis model established by using SAP2000,can better simulate the hysteresis property of the thin steel plate shear wall.

steel plate shear wall;shell unit model;equivalent pull rod model;finite element analysis;hysteresis performance

10.3969/j.issn.1009-8984.2017.03.004

2017-08-30

孙永亮(1981-)，男(汉)，陕西渭南，硕士。主要研究结构工程。

TU392.4

A

1009-8984(2017)03-0016-06