无刷直流电机换相转矩脉动抑制的研究

, ,

(上海理工大学 光电信息与计算机工程学院,上海 200093)

无刷直流电机换相转矩脉动抑制的研究

杨威,郝润科,高峰

(上海理工大学 光电信息与计算机工程学院,上海200093)

分析了无刷直流电机产生转矩脉动的原因,设计了自抗扰控制器来抑制无刷直流电机的转矩脉动的发生.以控制器本身的状态观测器检测系统的相电流脉动,通过控制器本身的非线性状态反馈控制器对检测电流脉动误差值进行补偿,从而抑制电流的波动.采用双闭环控制抑制转矩脉动的发生.仿真结果表明,设计自抗扰控制器抑制了系统干扰引起的超调量.反馈能够完全地被快递跟踪.设计的控制系统使无刷直流电机的转矩脉动值为9%左右.因此,自抗扰控制系统能够更好地抑制无刷直流电机转矩脉动的产生.

无刷直流电机; 自抗扰控制器; 转矩脉动; 抑制

无刷直流电机(brushless DC motor,BLDCM)由无刷直流电机本身、供电功率电路和转子位置检测电路等共同构成.在BLDCM控制系统中,转子位置检测电路替代有刷直流电机的机械换相装置.BLDCM控制系统中的转子位置检测电路是用来检测电机转子在正常运行时电机转子的位置[1-2].BLDCM拥有小体积、高效率、运行稳定和养护简单便捷的特点.但是,BLCDM在实际使用过程中有较大的转矩的脉动发生.这一问题限制了BLDCM在高精度控制领域中使用.BLDCM的转矩的脉动引起因素有以下5种:a.原理性电磁转矩的脉动,由非理想反感应电动势产生;b.齿槽效应产生的转矩的脉动;c.电枢反应产生的转矩的脉动;d.运转变相中,电流或感应电动势(反电动势)发生变化引起的转矩的脉动;e.加工电机中材料的不一致和机械精度不高存在的缺陷.在制造一台BLDCM时,谐波变化或电机齿槽引起的脉动转矩都很小.然而,在换相过程中,电流变化导致的转矩脉动较大,大约占50%.所以,分析和抑制换相所引起的转矩脉动,已经成为减小BLDCM 转矩波动的关键.国内外的学者从控制电路拓扑结构、电机驱动方法等角度提出了一些研究方向,采用电流反馈调节法、PWM (pulse width modulation)斩波控制和电流预测控制等方法抑制和消弭BLDCM 引起的转矩的脉动.但这些方法仍然不可避免地存在过补偿问题和欠补偿的缺陷.现实使用这些方法抑制转矩脉动减小的作用并不明显[3].本文提出用自抗扰控制(active disturbance rejection control,ADRC)方式抑制和消除无刷直流电机换相中引起的转矩脉动.通过实验证明,与传统电机控制方法相比,自抗扰控制器能够更好地抑制和消除转矩产生的脉动,从而使电机运转更加平稳可靠.

1 换相转矩脉动分析

换相转矩脉动(commuting torque ripple,CTR)产生的原因为换相过程中及电动势或电流变化使转子波动.电机转子的波动导致转矩脉动的产生.利用方波驱动三相BLDCM时,每次只有其中的两相(AB,BC或AC)处于导通状态,而另一相却处于关闭状态.BLDCM的稳态转矩的大小与换相电流有关.而换向电流与反电动势大小有关.BLDCM的稳定转矩脉动与反电动势和换相电流大小都有关.

假设BLDCM三相对称,星型连接,忽略电枢反应,不计涡流和磁滞损耗.BLDCM的三相电磁绕组的等效及驱动电路如图1所示.R1,R2和R3分别为三相定子绕组的电阻;L1,L2和L3分别为三相定子绕组的电感;eA,eB和eC分别为三相绕组上的反电动势,Ud为直流电源.Q1—Q6为绝缘栅双极型晶体管,D1—D6为二极管,构成了BLDCM全桥驱动电路.

图1 BLDCM的驱动与三相绕组等效电路Fig.1 Brushless DC motor drive and the equivalent circuit of three-phase winding

电机绕组都是电感性负载,换相转矩脉动发生时相电流以恒定速率升降.换相导致波形是梯形波,不是理想方波.在电机转动过程中,相电流关闭期内的降低速率和导通期内的升高速率并不相同.所以,非变相时,产生了电流波动,电流波动引起转矩脉动.以A相与C相导通后向B相与C相通电导通换相过程为例[4].在不同速度运动换相时,图2展示了各相变化的电流波形.iA,iB和iC为三相绕组中的电流,t1为关断时相电流变化下降的时间,t2为开通时相电流变化上升的时间.在变相中,由D4为A相续流并逐渐减小到零.B相的电流逐渐增大到一定值.式(1)为三相电机换相过程中的电路方程.

(1)

式中:L为三相绕组的自感;R为三相绕组的电阻值;t为各相电流变化的时间.

电机各相绕组感应电势为梯形波.设Em为感应电动势的幅值.在换相时eA=eB=-eC=Em.与绕组的时间常数L/R相比,PWM的周期近似属于无限小.忽略电枢绕组中阻值的影响,同时忽略A,B和C相的电流初值和终值的大小.各相电流未变化和变化之后的稳态值为I0.由方程(1)可得变相中BLDCM各相电流方程为

(2)

由方程(2)可得变相中A相绕组的关闭时间t1和B相绕组开通的时间t2为

t1=3LI0(Ud+2Em)

(3)

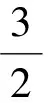
(4)

设BLDCM的转子的角速度为ω,则换相时电磁的转矩

(5)

由式(2)～ (5)可得:a.当4EmUd时,转速大于一个定值,两相绕组换相时电流变化不能够同步.iA已经降为0,但iB还没有达到稳态,即t2>t1.换相导致转矩变小,转矩的脉动为Te.换相情景如图2(c)所示[5].

通过以上分析可知,BLDCM换相时的时间随着转速的变化而变化.在低转速运行状态,换相引起的关闭时间大于导通时间.在高转速运行状态,变相导通时间大于关闭时间.从而导致BLDCM在变相过程中转矩脉动的大小随转速的变化而变化.以较高的速度运行时,BLDCM换相的过程引起的转矩变化加剧,从而使转矩的脉动变化增大.转矩随换相时间变化的方程为

(6)

图2 三相绕组换相的电流波形Fig.2 Three-phase current waveforms during winding commutation

2 设计ADRC抑制转矩脉动

ARDC由现代控制理论与PID相结合而得来.ADRC是在经典PID中引入现代控制中的状态观测器.ADRC包含状态跟踪微分控制器(state tracking differentiator,STD)、扩张观测状态控制器(expansion state observer,ESO)和非线性状态误差控制反馈器(nonlinear state error feedback control device,NSEFCD)三部分.STD根据控制系统的输入变量跟踪并获取系统中变化的微分信号,来解决响应与超调的矛盾.ESO主要目标是对扰动预估计,其根据被控研究对象确定的系统输入与输出,检测系统状况.NSEFCD通过非线性函数弥补线性组合的不足.因此,ADRC的算法简单、鲁棒性较强,同时不依赖系统的模型,而且还能够很好地监测系统中的内外干扰.但是,ADRC作为较复杂的非线性的被控制对象,研究时可以看作1个非线性的二阶控制系统,从而可以等效成2个一阶非线性结构并串联而成的控制系统.在建模时,首先进行BLDCM线性处理,构成一系列线性可控系统;然后设计适当的ADRC来实现控制[6].

BLDCM控制系统可以分别设计内、外环的一阶ADRC.控制转速的为外环子控制系统(一阶ADRC),控制转矩的为内环子控制系统(一阶ADRC).外环的一阶ADRC与预设值同时作用,并将输出的结果作为内环的一阶ADRC的预设值反馈给内环的一阶ADRC.通过控制BLDCM的转速n,从而完成对转矩Te的控制. ADRC同时实现了对控制系统中内、外干扰的监测,它能够不区分躯体受到干扰的形式而进行广泛的监测.STD调节系统响应超调,使系统运行平稳.非线性补偿装置监控系统干扰并适当地弥补.在图3的BLDCM转矩脉动控制系统中,ADRC将转矩脉动作为内部干扰进行监测并补偿,从而抑制转矩脉动,使转矩Te保持稳定.控制方案如图3所示[7-8].预先设定的定值,Σ2(x3,x4),Σ1(x1,x2)为ESO和STD获取的转矩和转速的超调量和干扰信号.n为电机稳定运行的转速.

图3 BLDCM的自抗扰等效控制框图Fig.3 ADRC equivalent control block diagram of the ADRC of BLDCM

2.1BLDCM的转速控制系统的设计

已知BLDCM三相的端电压方程为

(7)

式中:uA,uB和uC为A,B和C三相的相电压;L,M分别为A,B和C三相绕组的自感和互感.

BLDCM的电磁转矩方程为

Te=ω-1[eAiA+eBiB+eCiC]

(8)

BLDCM的机械运动方程为

(9)

式中:Tl为机械运动的负载转矩;B为机械运动的阻尼系数;J为机械运动的转动惯量.

由方程(9)得

(10)

令BLDCM的转速系统的扰动方程为

ω=-J-1Tl

(11)

由此可以得出BLDCM转速的一阶ADRC控制方程为

(12)

2.2BLDCM转矩控制系统的设计

令BLDCM转矩系统方程为

(13)

式中:p为极对数;ke为满足转矩方程所取的常数;ex为感应电动势;ix为电枢电流;s为转速与转矩反馈的反馈量.

若BLDCM采取两两导通.假设导通方式为AB.如果I为A/B两电枢电流,则A/B的总感应电动势e=eA+eB.us为A/B电枢两端电压.因此,可得BLDM的转矩方程为

(14)

令BLDCM转矩控制系统的扰动方程为

ω1=-pkese(L-M)-1

(15)

式中:ω1为BLDCM转矩控制系统的扰动.

由此可得BLDCM转矩的一阶ARDC方程组为

(16)

BLDCM转矩ADRC中的NSEFCD较为精准地检测转矩脉动,同时给转矩脉动恰当地抵偿,以实现约束转矩的脉动.

2.3串联系统中ADRC的设计

由以上分析可得串联控制系统的方程为

(17)

取BLDCM控制系统的非线性状态函数

(18)

式中:ε为输入函数引起的误差;α表示变化率,由函数增益变化引起;δ为微变化的正数.

选取非线性状态函数的目的是避免函数在零点振荡.当ADRC转矩脉动增益增大时,误差就会减小;反之,增益减小时,误差就会增大.因此,非线性状态函数使ADRC的性能更加优越.从而可得NSEFCD的方程为

(19)

式中:u0为电机控制系统中扰动误差的反馈控制函数;βi为NSEFCD设定而选取的适当参数.

则ADRC的最终控制量为

(20)

式中:u为电机控制系统中的最终控制函数;b0为取值范围内的定值;z(t)为ESO对扰动估计的观测量.

在设计ADRC时,必须根据研究的系统选择阶数,因为,系统决定了控制器的阶数.然而,ADRC不会受具体的被控系统或模型的限制,使应用变得更加广泛.BLDCM可以当作1个二阶非线性被控系统,从而需要2个一阶ADRC串联实现控制,且能够满足对转矩脉动和转速控制的要求.这也体现了ADRC的鲁棒性和适应性的一面.ADRC中STD,ESO和NSEFC方程如下:

STD方程

(21)

ESO方程

(22)

NSEFCD方程

(23)

式中:R11,α10,δ10,β11,α21,δ21,β22,β31,α22,δ22是ADRC的各个参数;k(t)是控制系统预设的初值;x11是预设定的输入跟踪的初值;x21是状态观测器ESO的观测量;x22是状态观测器ESO观测的扰动量;b10是控制系统中控制量变化的增益.

可以分别设置STD,ESO和NSEFCLD的相关参数.ADRC利用简单、高效的数学算法分析来实现对控制系统的反馈控制,同时能够很好地对系统的干扰进行监测和精确补偿.消弭超调和抵偿提高了控制系统的稳定性.

3 控制系统的仿真与分析

BLDCM的控制系统为双闭环控制.转矩和转速作为控制量,分别对其设计控制器.其中,外环为控制转速的一阶ADRC,内环为控制转矩的一阶ADRC.设计控制器并运用Matlab/Simulink中的S函数.仿真中BLDCM的参数如表1所示.

系统采取双闭环控制.实验过程中第一步设定转速的ADRC参数.第二步再加入转矩控制器中一起调试,从而确定整个控制系统中的参数[9-10].

转速控制的ADRC中函数ξ的参数值为

转矩控制的ADRC中函数ξ的参数值为

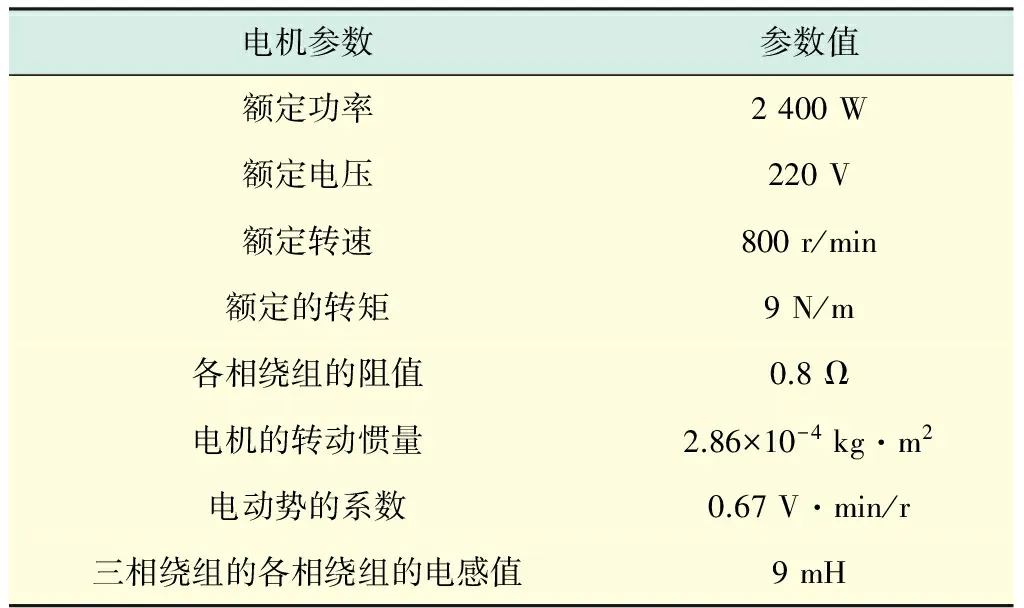
表1 BLDCM仿真参数设定表Tab.1 BLDCM simulation parameter settings

BLDCM分别在PI和ADRC控制下进行仿真,设给定转速n=800 r/min.电机转速的波形如图4和图5所示.图4是在带载情况下的转速波形,图5是在负载突变情况下的转速波形.对比图4和图5可得,ADRC控制下的转速平稳且超调量小.图6～8(见下页)分别为BLDCM在空载、负载和负载突变情况下的转矩波形.在0.3 s时突加负载,转矩瞬间变化,但很快就平稳,同时转速在负载突变的瞬间降低后又趋于平稳状态,如图9所示.从图9中可得,ADRC控制的转矩波形较平稳.在空载、负载和负载突变情况下,转矩脉动较小,同时转速比较稳定.

图4 转速曲线波形Fig.4 Rotational speed curve waveform

图5 在负载突加下的转速波形Fig.5 Speed waveform under sudden load

图6 自抗扰控制的空载转矩波形Fig.6 Torque waveform of no load ADRC

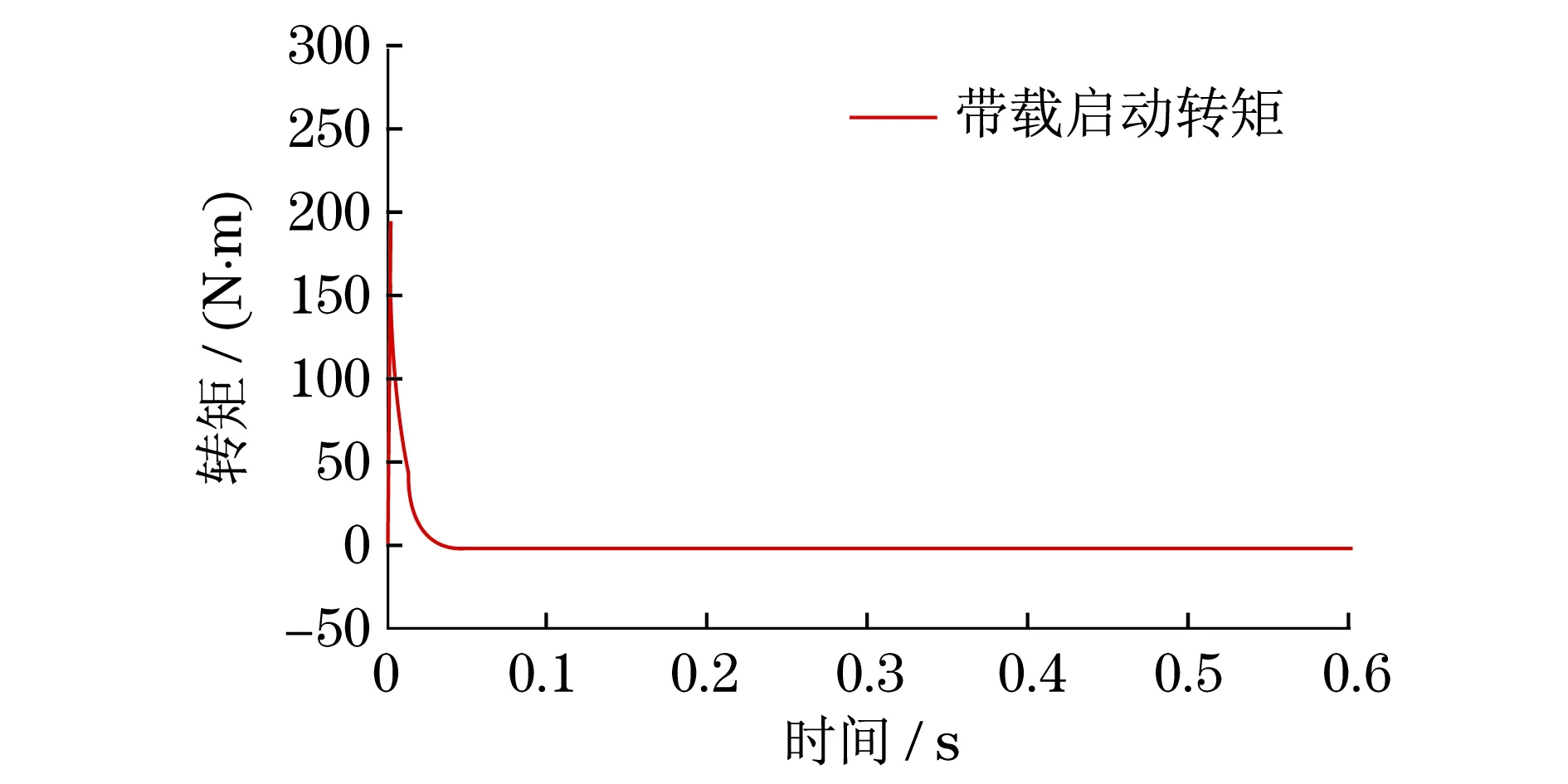
图7 自抗扰控制的带载启动转矩波形Fig.7 Start torque waveform of ADRC under load

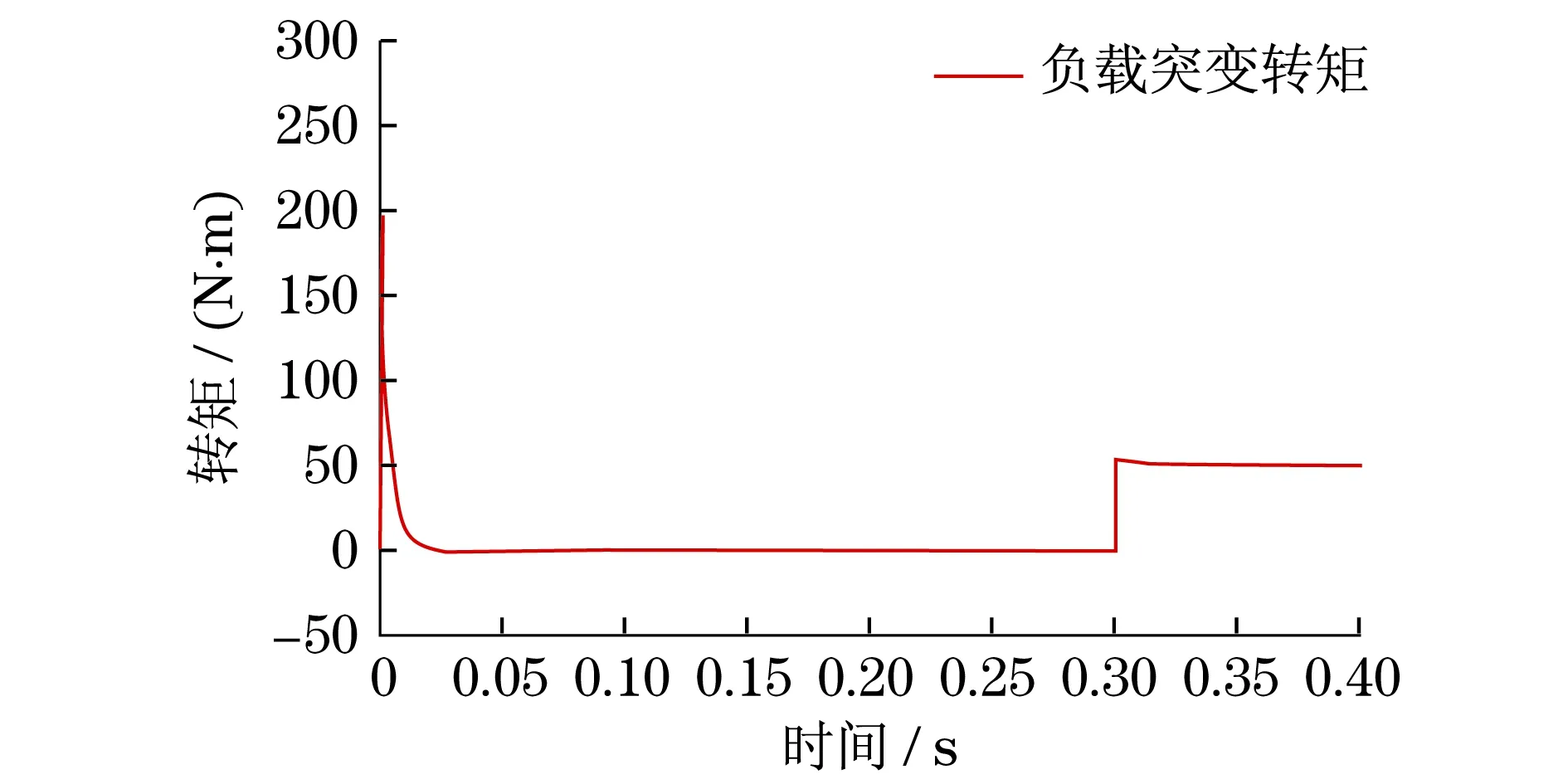
图8 负载突变情况下的转矩波形Fig.8 Torque waveform of ADRC under load variation

图9 负载突变情况下的转矩和转速波形Fig.9 Torque and speed waveforms of ADRC under load variation

综合分析可得,ADRC比PI在抑制转矩脉动方面具有更多的优势.ADRC具有良好的抑制转矩脉动的效果.通过仿真计算得出脉动值为9%,消弭响应产生的超调反馈被顺利跟踪.

4 结束语

设计了自抗扰控制器,抑制无刷直流电机转矩脉动.通过自抗扰控制器的观测器检测相电流的脉动,再通过控制器本身的非线性状态反馈控制率对检测到的电流脉动误差进行补偿抵消,实现消弭相电流波动来抑制脉动转矩.实验表明,自抗扰控制器相比PI控制器能更好地约束转矩脉动,使电机运转更加平稳可靠.

[1] SHI T N,LU N,ZHANG Q,et al.Brushless DC motor sliding mode control with Kalman filter[C]∥IEEE International Conference on Industrial Technology.Chengdu: IEEE,2008:1-6.

[2] 张琛.直流无刷电动机原理及应用[M].北京:机械工业出版社,2001.

[3] 谢宝昌,任永德.电机的DSP控制技术及其应用[M].北京:北京航空航天大学出版社,2005.

[4] 王海峰.无刷直流电动机转矩脉动控制技术的研究[D].西安:西北工业大学,2003.

[5] 韩京清.自抗扰控制器及其应用[J].控制与决策,1998,13(1):19-23.

[6] 强曼若.无刷直流电动机的发展与应用[J].微电机1995(1):23-25.

[7] 陈宇,张锐锋,徐贵光,等.大型火电机组协调系统的线性自抗扰控制[J].计算机仿真,2016,33(2):180-184.

[8] 韩京清.自抗扰控制技术——估计补偿不确定因素的控制技术[M].北京:国防工业出版社,2008.

[9] 黄庆,黄守道,陈泽远,等.不对称电压下PWM整流器的变结构自抗扰控制[J].电机与控制学报,2014,18(1):50-55.

[10] 黄本润,夏立,吴正国.自抗扰控制器在动态电压恢复器中的应用[J].电机与控制学报,2012,16(6):106-110.

SuppressionofBrushlessDCMotorCommutationTorqueRipples

YANG Wei,HAORunke,GAOFeng

(SchoolofOptical-ElectricalandComputerEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

The causes of the torque ripples of a brushless DC motor (BLDCM) were analyzed and an active disturbance rejection controller (ADRC) was designed to control the torque ripple reduction of the brushless DC motor.A state observer of the controller was adopted to detect the phase current ripple of the system.And the offset value of the detected current ripple deviation was compensated by the non-linear state feedback control rate of the controller to achieve the suppression of current ripple,which forms a BLDCM double closed-loop control system to achieve the suppression of torque ripple.The simulation results show the value of torque ripple of the brushless DC motor designed is 9%.The ADRC eliminates the overshoot generated by the system and the feedback can be fully and smoothly tracked.In short,the designed ADRC can better suppress the pulsation of the torque by compensating the offset of the current ripple error.

brushlessDCmotor;activedisturbancerejectioncontroller;torqueripple;suppression

1007-6735(2017)05-0467-06

10.13255/j.cnki.jusst.2017.05.010

2016-08-30

杨 威(1990-),男,硕士研究生.研究方向:电气拖动及控制.E-mail:yangwei_gsw1@163.com

郝润科(1965-),男,副教授.研究方向:电气拖动及控制.E-mail:h-rk@163.com

TH166;TG659

A

(编辑:石 瑛)