压气机稳定边界的数值预测研究

靳 楠，胡 骏，李 骏

（南京航空航天大学能源与动力学院，南京210016）

压气机稳定边界的数值预测研究

靳 楠，胡 骏，李 骏

（南京航空航天大学能源与动力学院，南京210016）

为研究不同压气机稳定性预测方法的准确性，采用最大静压升系数法与商用CFD软件，对某4级低速压气机的稳定边界进行了数值模拟，并与试验结果对比。计算结果表明：最大静压升系数法在预测压气机稳定边界上有一定的准确性。使用商用CFD软件NUMECA对某4级压气机进行模拟计算，考虑了不同的网格划分方案、使用不同的湍流模型和差分格式等因素，以出现数值发散作为压气机失稳的标准，结果表明：主流区的网格对计算结果影响较大。不同差分格式的结果显示，中心差分格式的结果最好。

轴流压气机；稳定边界；数值模拟；最大静压升；航空发动机

0 引言

航空燃气涡轮发动机的风扇/压气机的长度、质量在整台发动机中占比很大，生产、维护费用高昂，其性能不仅影响推重比、耗油率等性能参数，而且对整机稳定性也影响巨大，其性能优劣直接影响整机的研制。发动机的设计总是要求风扇/压气机在保持高效率和足够稳定裕度的条件下，实现以更少的级数达到更高的增压比，同时还要满足强度、可靠性、噪声、隐身等方面的要求[1]。为了增加发动机推重比、降低耗油率，风扇/压气机向高压比和高级负荷方向发展，必然使风扇/压气机端壁和叶片吸力面的附面层承受更大的逆压力梯度，在这种情况下风扇/压气机内部流动更容易分离，其稳定性就难以得到保证，因此对气动稳定性研究越发重要。航空发动机推重比的不断提高，需要高性能、高效率和高稳定性的风扇/压气机，也需要不断发展完善风扇/压气机气动设计体系中与之相适应的设计和计算方法。

自航空燃气涡轮发动机出现以来，压气机稳定性一直是压气机设计和研究人员关注的问题。随着研究人员对压气机内部流动认识的不断深入，主要有3类针对压气机稳定性的分析方法。第1类是经验关联法。在研究压气机稳定性的初期阶段，研究人员通过对大量的试验数据进行分析和理论的研究，建立起判断压气机失稳的准则参数，并将准则参数与压气机的几何参数和气动参数等关联起来，把准则参数作为压气机失稳的判断标准。在这阶段，Emmons[2]、Stenning[3]、Marble[4]、Sears[5]、Krieble[6]、Dunham、Lieblein[7]、Koch[8]等人随着研究的不断深入，提出了多种经验准则来评估压气机的稳定边界，其中代表性的有：Dunham提出了将特性线上压升系数对流量系数的导数为零点作为判定压气机失速的准则；Lieblein[8]提出了将扩散因子、扩散率作为叶栅失速发作的近似准则；Koch提出用压气机最大静压升系数来评估压气机的压升潜力[9]。这类型的方法依据试验数据，使用经验关系式来判断压气机状态点是否失稳，因此有一定的误差，但是其优点是使用简单、便捷。第2类方法以小扰动的线性稳定性理论为主，用于预测风扇/压气机或压缩系统的工作稳定性。该类方法已发展出考虑多叶片排的不可压缩和可压缩稳定性模型。自 20世纪 50年代以来，Emmons、Stenning[3]、Marble[9]、Sears、Fabri和 Moore 等人的工作都属于此类，用于稳定性分析的涡方法也大多属于此类方法。国内外学者对这一类方法进行了较多的研究与发展，具体成果见参考文献[10-11]；第3类方法基于压缩系统的动力学模型，不仅关心风扇/压气机或压缩系统在平衡工作点受小扰动的稳定性，还非常重视有限扰动对稳定性的影响及其发展情况，以及风扇/压气机失速后类失速流态—旋转失速和喘振的性质，这类方法为建立在时域上的时间推进法，以Moore和Greitzer的研究工作为代表[12-14],近年来此类方法得到了较大的发展，例如参考文献[15-16]。

1 方法介绍

C.C.Koch通过对大量的低速轴流式压气机试验结果和有限的高速风扇/压气机试验数据的分析，将风扇/压气机叶栅通道类比于2维扩压器，提出了最大静压升系数的概念来评估压气机的压升潜力[9]。将压气机的最大静压升能力与叶栅无因次长度比L/g2、工作雷诺数、无因次轴向间隙比△z/s和无因次径向间隙比ε/g关联起来，分别如图1、3、4、5所示。其中

t为栅距，而其他几何参数的定义如图2所示。

定义风扇/压气机运行过程中的气动有效静压升系数（Ch）ef，用来描述压气机某一工作状态的压升。当有效静压升超过压气机的压升潜力，即表示压气机失稳。

式中：V、W和U分别为绝对速度、相对速度和牵连速度；V1，ef为叶栅进口的有效动压头速度，定义为

其中：

当（α1+β1）≤90°时，Vmin=V1sin（α1+β1）

当（α1+β1）＞90°时，Vmin=V1

当 α1 ＜0° 时 ，Vmin=U（4）

当 β1＜0°时，Vmin=U

各速度分量的定义如图2所示。

图1中的结果是在Re=130000、无因次径向间隙ε/g=0.055、以及无因次轴向间隙△z/s=0.38的情况下获得的。以此为参考点，当这些参数变化时，需要对图1的结果进行修正，引入工作雷诺数、无因此轴向间隙、无因此轴向间隙的影响

（Ch）s=KRe×Kε/g×K△z/s×（Ch）s，ref（5）

式中：雷诺数修正系数KRe、叶尖间隙修正系数Kε/g和叶排轴向间隙修正系数K△z/s的取值分别由图3、4、5中的曲线确定。

2 基元叶栅法与判稳方法结合计算压气机稳定边界

压气机气动稳定性的基本技术问题就是在均匀进气的条件下稳定边界的预测以及稳定边界与其设计参数相关性的问题。稳定边界预测一般与非设计点性能预测结合使用。基元叶栅法就是利用已获得的关于基元叶栅的落后角和总压损失与其主要影响因素（如马赫数Ma，雷诺数Re和攻角i等）的关联式，结合无叶区流场的计算预测压气机非设计点的气动性能。有关基元叶栅法的详细介绍请参见文献[17]。通过基元叶栅法得到压气机流场信息，如速度、压力、温度等参数，根据流场信息，依靠最大静压升系数法[9]即可判断压气机是否稳定。

本文将基元叶栅法与最大静压升系数法相结合，发展了1种预测压气机稳定边界的数值方法，并以某4级低速压气机为算例，验证了该方法的有效性。

所用的压气机为4级低速模拟压气机，采用类重复级设计，第3级为模拟级，前2级和第4级分别为模拟级提供恰当的进、出口条件，其设计转速为900 r/min，外径为1.5 m，轮毂比为0.88，转子叶尖速度为70.7 m/s，转、静子展弦比分别为0.957与1.5，转子与静子中径处叶栅稠度分别为1.528、1.625。

试验得到的压气机特性线与计算结果如图6所示。分别对低速压气机在设计转速为900、700、500 r/min下的试验结果与计算结果做了对比如图7所示。

不同转速下边界点流量和压比的相对误差如图8所示。从图中可见，基元叶栅法与最大静压升系数法结合计算所得的稳定边界与试验结果比较接近，边界点相对误差如图8所示。

使用最大压升系数法判断压气机稳定边界，得到压气机在不同转速 (500、700、900 r/min)下，静压升系数的 4 级分布，分别如图 9（a）、（b）、（c）所示。

从图中可见，在不同转速下，静压升系数的4级分布趋势非常一致。4级的失速静压升系数几乎相同，由此表明4级的压升潜力差别不大，这是因为所用的4级压气机为类重复级压气机，各级叶片几何结构近似相同导致的。在不同流量点下，有效静压升系数逐级增大，在失速点均为第4级时有效静压升系数超过了最大静压升系数，计算结果表明压气机的第4级首先出现失稳的现象。在失速点处各级的静压升系数差别不大，且比较接近最大静压升系数。

3 4级低速压气机数值模拟研究

为了校验数值模拟结果的可靠性，同时找到最优的数值模拟方法，使用商用软件NUMECA对4级压气机进行数值计算，以出现数值发散作为压气机失稳的标准，得到压气机稳定边界。分别改变网格划分方式、湍流模型以及差分格式进行计算，将计算结果与试验结果进行比较，比较不同的网格、湍流模型、差分格式对CFD计算的稳定边界的影响，并与实验结果做出对比。

3.1 不同网格划分方式数值模拟的结果分析

合适的网格生成技术往往是正确模拟一些复杂流动的关键所在，通过改变网格的分布情况及控制总网格量，主要从主流区均匀网格百分比、叶尖间隙内网格节点数以及总网格量（改变叶片区网格量）3方面考虑，得到6种不同计算网格（见表1），分别进行计算后寻找理想的网格划分方式。6种不同网格划分方式中Grid1～Grid4的总网格量均接近500万，故近似认为他们总网格量相同；由于模型压气机的设计采用类重复级设计，故所有静子叶片（包括进口导叶）网格量相同，所有转子叶片网格量也相同。除网格不同外其余计算条件均相同。

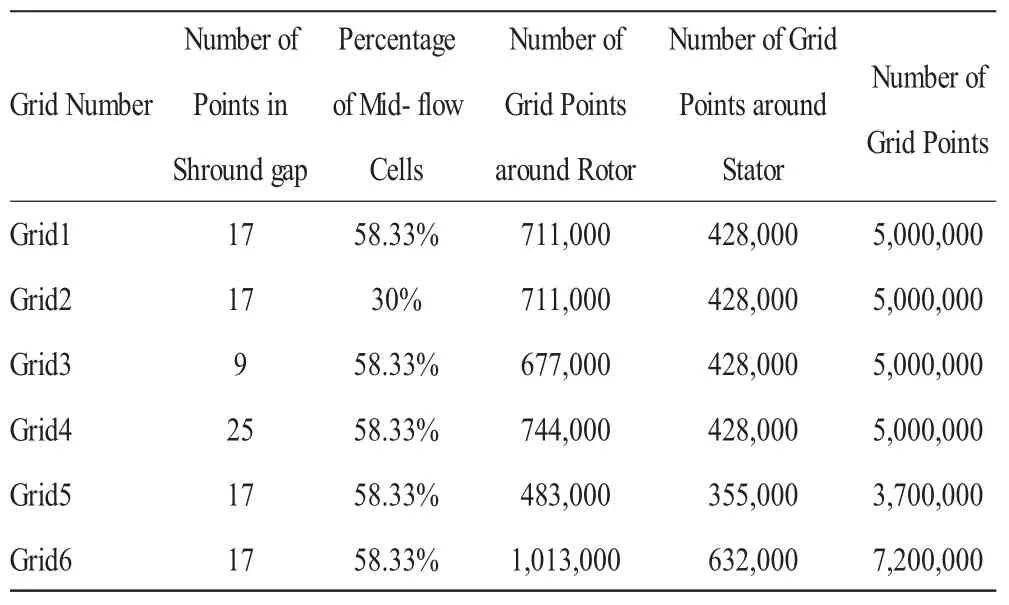
表1 网格设计方案

在设计转速下压气机特性如图10所示。从图10（a）中可见，大流量点的效率均偏离试验数据较大，Grid2整体比试验数据偏低。从图10（b）中可见，除Grid2外，其他算例的压比特性均比试验值高，Grid1与Grid6的压比特性几乎重合。考虑CFD方法计算的压气机稳定边界点，Grid5和Grid2的边界与试验结果最为接近。

Grid1、Grid2、Grid3、Grid4 以及试验数据在边界点的压比特性比较如图11所示。从图中可见，4个算例总网格量均相同，与Grid1相比，Grid2主流区网格占比减少，Grid3叶尖间隙网格数减少，Grid4叶尖间隙网格数增加。主流区网格占比对计算的而稳定边界影响较大。

Grid5、Grid1、Grid6 的网格量分别为 300 w、500 w、720 w，叶尖间隙网格量、主流区网格量占比均相同。边界点流量和压比相对误差如图12所示。从图中可见，Grid5计算的稳定边界流量与试验值最为接近，但是边界点压比与试验值相差最大。而Grid1与Grid6稳定边界流量与试验值差别较大，但是压比与试验值较为接近。500 w网格与720 w网格的计算结果相差不大。

3.2 不同湍流模型数值模拟结果分析

在利用原始变量求解雷诺平均N-S方程组时需用湍流模型对其进行封闭求解，故湍流模型的选择是影响压气机内部流动数值模拟精度的重要因素。在选定Grid1网格划分方式的基础上改变计算中所使用的湍流模型，与试验进行比较分析，得到较为理想的湍流模型。所采用的湍流模型有S-A（Spalart-Allmaras）模型（一方程模型，鲁棒性较好，能较好地解决一些复杂流动）、Yang-Shih k-ε模型（两方程模型，低雷诺数湍流模型，可以更加精确地求解壁面附近的流动）以及SST k-ω模型（两方程模型，改进后的k-ω模型，在广泛的流动领域中有更高的精度和可信度）。在计算中，除湍流模型不同外其余计算条件均相同。

不同湍流模型计算所得的压比特性和效率特性如图13（a、b）所示。从图中可见，压比特性线均高于试验值，效率特性线在小流量点上与试验值接近，在大流量点上与试验值差别较大。就稳定边界而言，使用k-ε模型所得到的稳定边界最接近试验所得边界。

使用不同湍流模型所得的边界点流量均与试验值有一定差别，相对误差如图14。

3.3 不同差分格式数值模拟结果分析

在数值模拟中选择合理的计算格式进行计算可以提高数值模拟的精度，进而解决一些较为复杂的流动问题。本节是在前两节的基础上，选定Grid1的网格划分方式，S-A湍流模型，对N-S方程中空间项的离散方法进行改变，将计算得到的结果与试验结果进行比较分析，得到较理想的计算格式。本文中差分格式分别采用中心差分格式及迎风格式（TVD格式和通量差分格式，均为2阶精度）。在相同计算条件下，中心差分格式计算得到的结果误差比迎风格式更小，但当流动中出现如激波这样的间断时，中心差分格式的数值解会产生波动，得到的结果误差会较大；TVD格式是建立在非线性限制器的概念上的，力图阻止数值波动的产生，使得数值解的变化以非线性的方式得以控制；通量差分格式是在每个网格步求解时对相邻间断的控制方程进行描述。本节的计算，除空间差分格式不同之外其余计算条件均相同。

改变差分格式计算所得的压比和效率特性如图15（a、b）所示，从图中可见，压比特性均高于试验值，中心差分格式与TVD格式在小流量点的效率特性与试验值较为符合，大流量点的效率特性与试验值差别较大，通量差分格式效率特性与试验值符合度较差。就稳定边界而言，使用TVD格式计算出的边界点与试验值差别较大。总而言之，TVD格式对特性的模拟效果较差。

边界点流量和压比相对误差如图16（a、b）所示，从图中可见，中心差分格式边界点流量和压比与试验最接近。TVD格式边界点流量与压比偏离试验值最远。中心差分的计算结果最好。

4 总结与展望

针对4级低速模拟压气机的稳定边界，以最大静压升系数法为主要方法，商用CFD软件数值模拟为参考，进行了一系列的数值计算，并与试验结果做出对比。得到的主要结果如下：

（1）使用最大静压升系数法判断压气机的稳定边界有一定的准确性。

（2）分析通过改变网格划分方案的计算结果，主流区网格占比对压气机稳定边界影响较大。分析不同差分格式的结果，中心差分格式的结果最好。使用NUMECA计算的压气机稳定边界与试验结果有一定的误差。下一步的工作将会围绕使用最大静压升系数法修正CFD计算结果来展开。

[1]刘永泉.国外战斗机发动机的发展与研究[M].北京：航空工业出版社，2016，261-262.LIU Yongquan.Development and investigation of foreign fighter engine[M].Beijing:Aviation Industry Press,2016：261-262.(in Chinese)

[2]Emmons H W,Pearson C E,Grant H P C.Compressor surge and stall propagation [J].Transactions of the ASME,1955，77（4）:455-469.

[3]Stenning A H,Kriebel A R,Montgomery S R.Stall propagation in axial-flow compressors[J].Massachusetts Institute of Technology,1956,115:163-8.

[4]Marble F E.Propagation of stall in a compressor blade row[J].Journal of Aeronautical Sciences,1955,22（8）:541-544.

[5]Sears W R.Rotating stall in axial compressors [J].Zeitschrift für Angewandte Mathematik und Physik,Birkhäuser Verlag AG Basel,Switzerland,1955,35（6）:429-455.

[6]Kriebel A R,Schuuind R G.Stall propagation in a cascade of airfoils[R].NACA-TRR-61,1960.

[7]Leiblein S,Roudenbush W H.Theoretical Loss relation for low-speed two dimensional cascade flow[R].NACA-TN-3662,1956.

[8]Koch C C.Stalling pressure rise capability of axial flow compressor stages[J].Journal of Engineering for Power,1981,103:645-656.

[9]Marble F E.Propagation of stall in a compressor blade row[J].Journal of Aeronautical Sciences,1955，22（8）：541-544.

[10]刘超.燃气涡轮发动机整机稳定裕度数值模拟方法研究[D].南京航空航天大学,2012.LIU Chao.Aerodynamic stability numerical simulation method study of compressor component running in gas turbine engine[D].Nanjing University of Aeronautics and Astronautics,2012.(in Chinese)

[11]侯睿炜,孙晓峰.一种基于数值计算的轴流压气机旋转失速稳定性模型——之一:理论模型及算法分析[J].航空动力学报,2009,24（12）:97-104.HOU Ruiwei,Sun Xiaofeng,Liner stability model of rotating stall based on direct numerical techniques:part I-theoretical model and algorithm[J].Journal of Aerospace Power,2009,24(12):97-104.(in Chinese)

[12]Moore F K.A theory of post-stall transients in axial compression systems:part I—development of equations[J].Journal of Engineering for Gas Turbines&Power,1986,108（1）:68-76.

[13]Greitzer E M,Moore F K.A theory of post-stall transients in axial compression systems:part II—application[J].Journal of Engineering for Gas Turbines&Power,1986,108（2）:231-239.

[14]Moore F K.Stall transients of axial compression systems with inlet distortion[J].Journal of Propulsion&Power,2015,2（6）:552-561.

[15]张环.旋转总压畸变对压气机稳定性影响的研究[D].南京航空航天大学,2009.ZHANG Huan,An investigation of effects of rotating total pressure distortion on aerodynamic stability of compressors[D].Nanjing U-niversity of Aeronautics and Astronautics,2009(in Chinese)

[16]王聪,文彬鹤,司文杰,等.轴流压气机旋转失速建模与检测:Ⅰ——基于确定学习理论与高阶Moore-Greitzer模型的研究[J].自动化学报,2014,40（7）:1265-1277.WANG Cong,WEN Binhe,SI Wenjie,et al,Modeling and detection of rotating stall in axial flow compressors:part I-investigation on high-order M-G models via deterministic learning[J].Acta Automatica Sinica,2014,40（7）:1265-1277.(in Chinese)

[17]Johnsen I A,Bullock R O.Aerodynamic design of axial-flow compressors[R].NASA SP-36.1965.

Numerical Predicting Study on Compressor Surge Margin

JIN Nan,HU Jun,LI Jun
（College of Energy and Power Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China）

In order to evaluate the accuracy of different method in predicting surge margin of axial compressor,a fourth-stage lowspeed model compressor was numerically simulated by maximum pressure rise method and commercial CFD software MUNECA,and the result was compared to experiment data.The calculation result shows that the maximum pressure rise method has certain accuracy according to experiment data.The simulation calculation of a fourth stage compressor was performed using NUMECA software,considering the influence of meshing means,different turbulence models and different scheme on surge margin,and taking numerical divergence as the instability standard of compressor.The results show that the factors in consideration all influence the accuracy of the simulation results,especially grid percentage of mid-flow cells,and the result of central difference scheme is the best in three schemes.

axial compressor;surge margin;numerical simulation;maximum pressure rise method;aeroengine

V231.3

A

10.13477/j.cnki.aeroengine.2017.04.009

2016-11-16

靳楠（1991），男，在读硕士研究生，主要研究方向为内流气动热力学；Email:jinnan666@foxmail.com。

靳楠，胡骏，李骏.压气机稳定边界的数值预测研究[J].航空发动机，2017，43（4）：48-55.JINNan，HUJun，LI Jun.Numerical predictingstudy on compressor surge margin[J].Aeroengine，2017，43（4）：48-55.

（编辑：张宝玲）