多端口石墨烯系统中的非局域电阻∗

王孜博 江华 谢心澄

1)(中国工程物理研究院微系统与太赫兹研究中心,成都 610200)

2)(中国工程物理研究院电子工程研究所,绵阳 621999)

3)(苏州大学物理与光电能源学部,苏州 215006)

4)(苏州大学高等研究院,苏州 215006)

5)(北京大学物理学院量子材料科学中心,北京 100871)

6)(量子物质协同创新中心,北京 100871)

多端口石墨烯系统中的非局域电阻∗

王孜博1)2)江华3)4)†谢心澄5)6)

1)(中国工程物理研究院微系统与太赫兹研究中心,成都 610200)

2)(中国工程物理研究院电子工程研究所,绵阳 621999)

3)(苏州大学物理与光电能源学部,苏州 215006)

4)(苏州大学高等研究院,苏州 215006)

5)(北京大学物理学院量子材料科学中心,北京 100871)

6)(量子物质协同创新中心,北京 100871)

(2017年9月21日收到;2017年10月7日收到修改稿)

非局域电阻,石墨烯,自旋霍尔效应,谷霍尔效应

1 引 言

非局域测量方法特指在电流流经区域以外对电压信号的测量,并以非局域电阻的形式体现.一种产生非局域电阻的方法是使得电流路径不同于经典的欧姆方式[1−3].例如,在量子霍尔效应中,电流可以在样品表面输运而体区域保持绝缘[4].另一种获得非局域电阻信号的方法是引入除电荷以外的其他自由度,例如自旋.这时的自旋流会由于自旋轨道耦合相互作用而偏离外场所引导的方向.由于非局域电阻通常起源于某些难以直接探测的非平庸物理相互作用,所以非局域测量现在已经成为一种用来在新材料中观测某些电磁学现象的强有力工具,并在多端口石墨烯体系中得到广泛的应用[5−10].

目前,已经在含如下三种效应的多端石墨烯体系中实验观测到非局域电阻.

1)自旋霍尔效应(spin Hall effect,SHE).SHE是一种由自旋轨道耦合导致的、使得电流在流过样品时在其垂直方向产生自旋流的输运现象[11−17].由于只有自旋而不是电荷在自旋输运中积累,且石墨烯的自旋轨道耦合强度非常小,以至难以直接在石墨烯中观测到SHE.借助于非局域测量方法,人们可以在外加垂直电场或磁场的单层石墨烯、氢掺杂的石墨烯等多端H形样品的狄拉克点或电中性点(charge neutral point,CNP)处观测到一个巨大的非局域电阻峰值[5,6].在排除了经典欧姆输运等方式后,基本可以确定自旋轨道耦合机理的存在.最近的理论研究还发现,对非局域电阻峰值的贡献不仅取决于SHE,经典的准弹道输运、准扩散输运、甚至无序吸附形式等都可能会对非局域电阻的性质产生重要的影响,其贡献可比甚至超过SHE本身[18,19].因此,如何能够在实验中进一步压制这些干扰源而得到纯的完全由SHE诱导的非局域电阻非常值得深入思考.

2)塞曼自旋霍尔效应(Zeeman spin Hall effect,ZSHE).ZSHE类似SHE,区别在于ZSHE通过外磁场打开自旋简并而不是自旋轨道耦合来产生自旋流[5,20−23].实验发现,相比于零磁场,外加垂直磁场的石墨烯样品可以测到一个远大于前者的非局域电阻[5],这意味着此时的非局域电阻极有可能是由ZSHE诱导的.

3)谷霍尔效应(valley Hall effect,VHE).在打破空间反演对称性的石墨烯中,谷指标可以起到类似自旋在SHE中的作用[24].最近人们在与衬底公度的石墨烯和外加偏压的双层石墨烯样品的CNP附近同样观测到了巨大的非局域电阻[7−9].但是由于此时的石墨烯在CNP处打开能隙,这意味着这些巨大的非局域电阻出现在了能带的带隙中,这是极其令人费解的现象[25,26].在排除了SHE、边缘态输运及热输运等机理的可能后,人们倾向于认为这个非局域电阻信号可能是由VHE导致的.目前,对于打开能隙的石墨烯中的谷电流探测缺乏直接的实验证据,因而人们非常希望通过这个可能由VHE诱导的非局域电阻来判断VHE的存在性.

综合来看,对于多端石墨烯样品中的非局域电阻,目前的研究不仅缺乏对其物理性质的深入理解,甚至对其产生机理本身仍存在较大的争议.本综述按照SHE,ZSHE和VHE的顺序详细地介绍相关的多端口石墨烯非局域电阻实验以及与之对应的理论和数值分析,希望能够帮助科研工作者了解目前非局域电阻研究的前沿进展,并对未来的非局域电阻研究起到帮助作用.

2 SHE在石墨烯体系中诱导的非局域电阻

SHE是一种由自旋轨道耦合导致的、使得自旋非极化的电流在流过样品时在其垂直方向产生自旋流或者垂直边界产生自旋积累的输运现象[11−17].这里的自旋轨道耦合是一种粒子自旋和“磁场”的相互作用,有趣的是,这个“磁场”并非真实存在而是由粒子相对周围电场的运动而导致.因此,不同于传统霍尔效应,实现SHE不需要外加破坏时间反演对称性的磁场.

为了定义电荷流通过SHE产生自旋流的强弱,一般使用自旋霍尔角θsH的概念,即产生的自旋流与原电荷流的比值.如图1(a)的四端系统所示,由端口1入射电荷流大小为I1=I↑+I↓0且自旋流大小为Is1=I↑−I↓=0的电流,SHE导致端口2,3产生电荷流大小为0而自旋流大小为Is2=I↑+I↓0的纯自旋流.则自旋霍尔角定义为

进一步地,(1)式可以利用电导的定义改写为

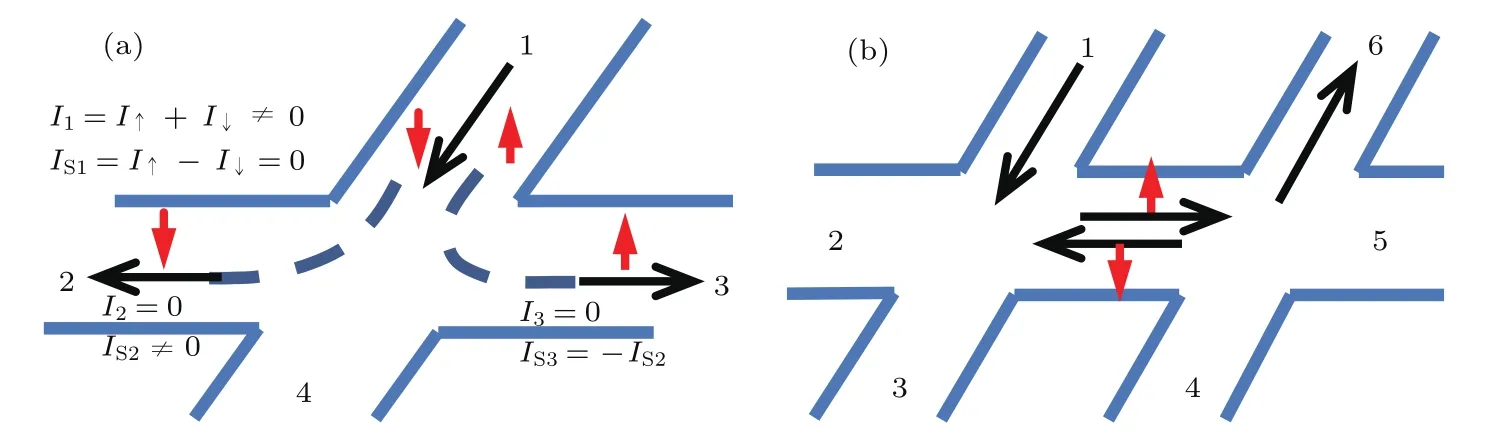
图1 SHE诱导非局域电阻示意图(红色箭头代表自旋指向) (a)四端体系中,由于SHE,电荷流I1转化为电荷为0的自旋流Is2;(b)六端体系中一个完整的由电荷流经SHE和ISHE转化为远端非局域电荷流的示意图Fig.1.The schematic diagram for the nonlocal resistance induced by the SHE:(a)In a four-terminal system,the charge current I1can be converted to charge mediated spin current Is2due to the SHE;(b)in a six-terminal system,the charge current is converted to a nonlocal one in a remote region due to the SHE and the ISHE in turn.The arrows colored by red indicate the spin directions.

其中σxy是自旋霍尔电导,σxx是纵向电导.由于Landauer-Buttiker公式可以直接给出电导表达式,所以(2)式更利于理论计算.

类似于SHE,入射的纯自旋流还可以通过逆自旋霍尔效应(inverse spin Hall effect,ISHE)转化为垂直方向的电荷流[27−29].在一个如图1(b)所示的六端系统中,端口1的入射电流I1通过SHE首先产生在端口2和5方向输运的自旋流,这个自旋流随后通过ISHE可以在端口3和4方向重新产生电荷流.这意味着可以在端口3和4测到一个非局域电压VNL=V6−V4和非局域电阻RNL=VNL/I1.由于自旋流不带电,其通常难以直接测量.而通过探测VNL和RNL等非局域信号,可以在实验上方便地确认SHE的产生.由于纯净的石墨烯材料中自旋轨道耦合强度非常小,通常难以观测到本征石墨烯中的SHE.目前,非局域电阻实验通常试图通过掺杂金、银、铜等重金属以增强石墨烯的自旋轨道耦合强度[30].同时,也有文献表明元素质量小的氢掺杂也可以增强石墨烯中的自旋轨道耦合[6].

2.1 SHE对非局域电阻性质的影响

借助于非局域电阻的测量,实验上可以在H形石墨烯样品的狄拉克点处观测到一个巨大的非局域电阻RNL.Abanin等[31]发展了一套理论,能够非常好地解释这个非局域电阻的起源.更重要的是,他们还给出了一个非局域电阻RNL和局域电阻RL的简单关系式:RNL.然而,这个关系式在解释某些实验现象时遇到了一些问题.具体而言,除了RNL在狄拉克点的巨大峰值以外,实验中还发现了另一个有意思的现象:对比于RL,RNL在费米能偏离狄拉克点时会更加急剧地衰减到0.例如,在本文的图13(a)中,红线所代表的非局域电阻RNL在Vg=1 V时已经衰减到几乎为0,而黑线所代表的局域电阻RL仍在衰减过程中.这个新奇的现象看起来似乎与经典的理论公式相矛盾,因为已经等于0的RNL不可能正比于不为0的,因而非常值得研究.

最近,在外加垂直电场引入自旋轨道耦合的情况下,如图2所示,北京大学陈剑豪实验组在H形石墨烯样品中同样探测到了一个巨大的非局域电阻信号.类似地,非局域电阻RNL相比RL依然迅速衰减.为了描述这个非局域输运现象,首先考虑一个含Rashba效应的H形四端单层石墨烯系统[18].如图3所示,电荷流从电极1向电极2纵向入射,在中心区通过SHE转化为横向的自旋流,最终通过ISHE转化为纵向电荷流,并作为非局域信号被电极3和4探测到.系统的哈密顿量可以写为

图2 外加垂直电场的H形石墨烯中局域电阻RL和非局域电阻RNL实验数据(Vbg代表样品背门电压,Vtg代表样品顶门电压,二者的差值引入垂直电场.在实验中,针对每一个固定的Vtg,Vbg从−60 V扫到60 V.由于费米面EF可以近似地由(Vtg+Vbg)/2决定,图中Vbg的变化等价于EF的变化.摘自北京大学陈剑豪教授的未发表数据)Fig.2.The local resistance RLand the nonlocal resistance RNLin an H-shaped graphene system with perpendicular electric field.In this fi gure,Vbgand Vtg stand for the bottom gate and the top gate voltage,whose di ff erence induces the electric field.In the experiment,Vbgsweeps from−60 V to 60 V with a fi xed Vtg.Since the fermi energy EFis approximately determined by(Vtg+Vbg)/2,the change of Vtgin this fi gure is equivalent to that of EF.Adapted from the unpublished data from J.H.Chen in Peking University.

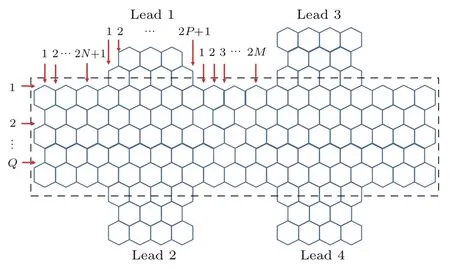
图3 H形四端石墨烯体系示意图(计算中电流从电极1流入,电极2流出,黑色虚线的矩形处为中心区)[18]Fig.3.The schematic diagram of the proposed H-shaped four-terminal graphene system[18].The current is injected into lead 1 and flows out from lead 2.The rectangle,denoted by the black dashed line,is the center region.

其中,和ci分别代表格点i的产生和消灭算符,εi是在位能,λR是外加Rashba耦合强度.为了模拟金属电极,四个端口的在位能均定义为εUD,这个在位能可以通过门电压调节.无序只存在于中心区并使用均匀分布在[−w/2,w/2]的安德森无序描述,其中w是无序强度.中心区的示意图用参数M,N,P和Q标记.例如,在图中的系统为M=3,N=2,P=4及Q=3.通过Landauer-Buttiker公式计算,在图4中得到局域电阻RL=(V1−V2)/I1及非局域电阻RNL=(V3−V4)/I1.

图4中的蓝线和红线分别展示了局域电阻RL和非局域电阻RNL随费米能EF的变化.在图中,Rashba自旋轨道耦合强度λR从0增加到0.3,而其他参数保持不变.可以发现这四张图主要体现出三个特点.

首先,非局域电阻在图4(a)中表现出负值,这里的“负”意味着当电流从电极1流向电极2时,电极3测到的电压竟然比电极4低.类似地,尽管不是严格的负数,但也可以在图4(b)中观测到相同的趋势(即一对出现在EF=±0.1附近的谷底).这个现象可以由以往实验中预言的准弹道输运机理来解释[32].具体而言,从电极1入射的载流子可以直接从电极4射出而不需要返回电极2.也就是说,可以在电极4测到一个正电压而在电极3测到一个负电压,这意味着非局域电阻RNL=(V3−V4)/I1此时是一个负值.因此,如图5所示,可以得到结论:非局域电阻RNL由以下三部分构成

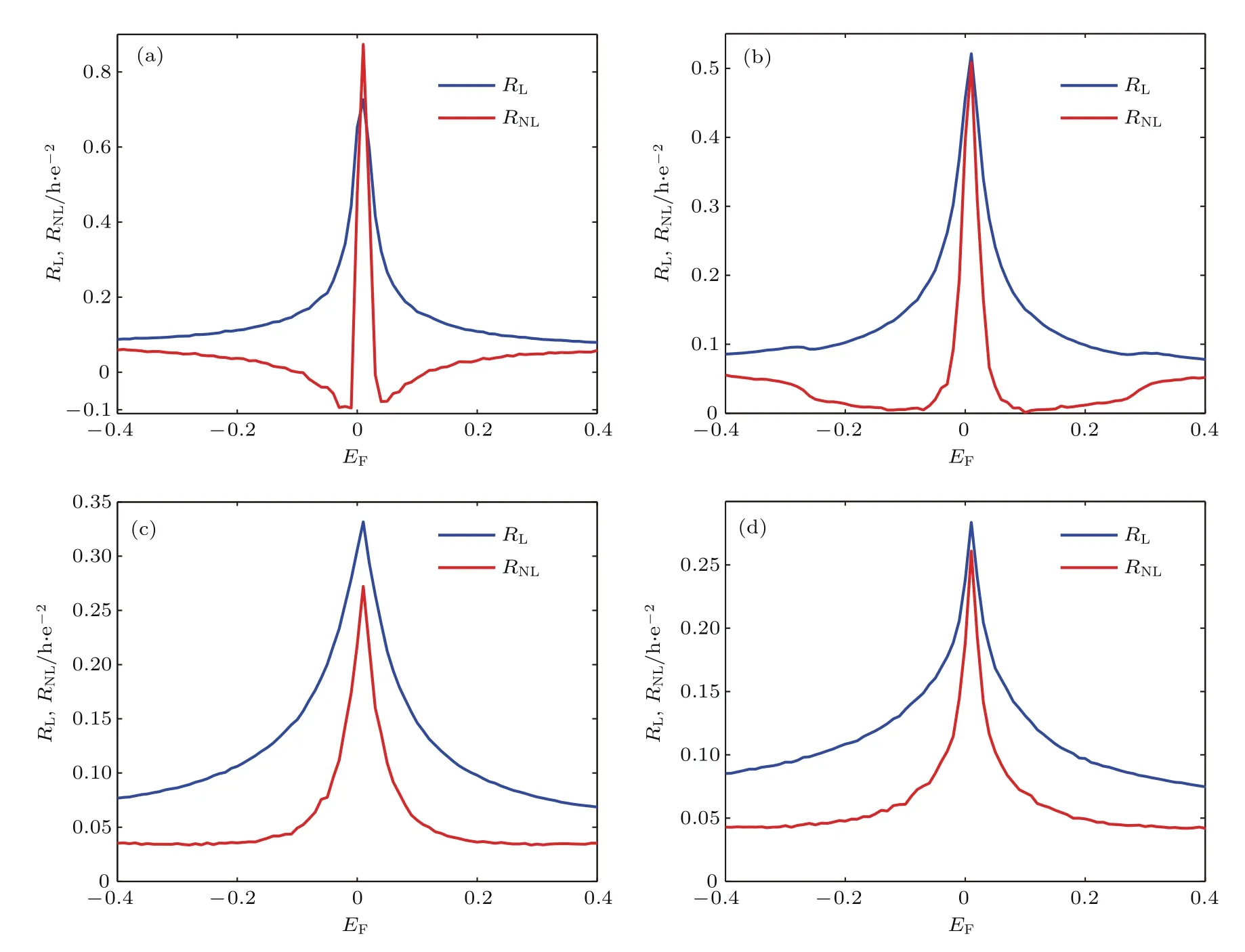
图4 局域电阻RL和非局域电阻RNL分别用蓝色和红色在图中标出(为了增强对比度,非局域电阻RNL放大了7.5倍)[18] (a)λR=0;(b)λR=0.1;(c)λR=0.2;(d)λR=0.3;安德森无序取为w=1Fig.4.The local resistance RLand the nonlocal resistance RNLare drawn in the blue and red lines,respectively[18]:(a)λR=0;(b)λR=0.1;(c)λR=0.2;(d)λR=0.3.The Anderson disorder strength is chosen as w=1.In order to make the comparison clear enough,the value of RNLis ampli fi ed by 7.5 times.

图5 三类输运机理的示意图(电流从电极1入射,并从电极2出射;红线代表准弹道输运机理下的Rballistic,这对于RNL贡献负值;黄线代表经典扩散Rclassic;绿线代表SHE导致的RHall;箭头代表从电极1入射的电流传播方向)[18]Fig.5.The schematic diagram for three kinds of transport mechanisms[18].The electron current is injected into lead 1 and then flows out from lead 2.The red line stands for the quasiballistic transport mechanism Rballistic,which makes a negative contribution to RNL.The yellow line represents the classic diffusion Rclassic.The green line denotes the spin Hall transport RHall.Arrows indicate the direction of the electron current which is injected into lead 1.

图5中红色标记的第一项Rballistic为刚讨论过的准弹道输运;棕色标记的第二项Rclassic代表经典扩散,也就是欧姆电阻的产生机理;绿色标记的第三项RHall起源于(3)式中的Rashba自旋轨道耦合,电流通过左侧纵向区域时由于SHE会产生一个与电流方向相垂直的自旋流,并最终在右侧的纵向区域由于ISHE而重新转化为电流.

第二,局域和非局域电阻均关于原点对称且在EF=0处达到极大值.重要的是,类似于在实验中观察到的情况,非局域电阻RNL相比局域电阻RL迅速衰减到0.例如,在图4(c)中可以发现当|EF|＞0.2时,非局域电阻几乎已经完全衰减到0并保持RNL=0.04h/e2,相反局域电阻仍在衰减过程中.这个奇异的现象与实验结果一致却与已知公式[31]

相矛盾.实际上,这个矛盾似乎可以由负数部分的非局域电阻来解释.具体而言,非局域电阻的基础值是RNL=Rclassic+RHall,其很可能满足(5)式.然而,根据(4)式,RNL中还存在一个叠加项Rballistic.由于Rballistic值为负,很自然地RNL会比理论预言(5)式更迅速地衰减到0.

第三,如图4所示,可以观察到的非局域电阻性质和Rashba效应间的惟一关联是非局域电阻的负数值趋势随Rashaba耦合强度λR的增加而减弱.相对应地,非局域电阻相比局域电阻的迅速衰减现象也逐渐消失.这对于理解非局域电阻与SHE间的内在机理仍远远不够.事实上,仅凭图4,甚至不知道非局域电阻的迅速衰减与SHE间是否存在关系.因此,除了图中所计算的RNL,得到一个纯的完全由SHE诱导的非局域电阻RHall就显得尤为重要.

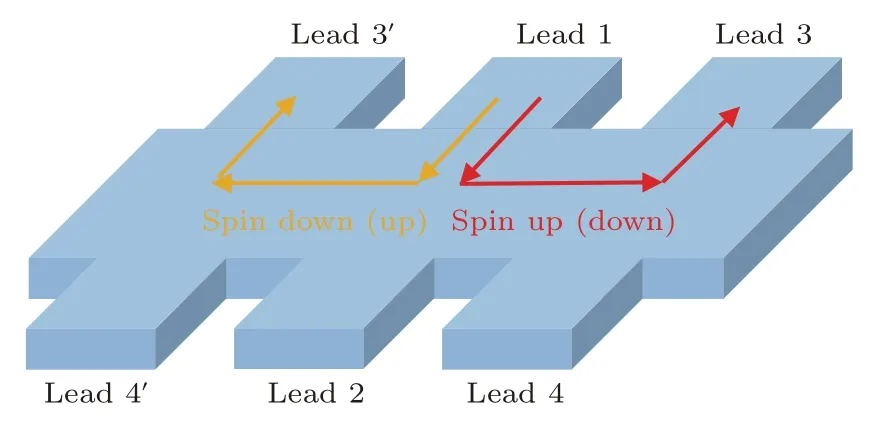
图6 新设计的六端系统示意图(新增加的电极3′和4′与电极3和4呈镜面对称;如果自旋向上(下)的自旋流从电极1沿着红线输运,则根据对称性,自旋向下(上)的自旋流必定沿黄线输运)[18]Fig.6.The schematic diagram of the proposed sixterminal system[18].Newly added lead 3′and 4′locate at a mirror symmetry to lead 3 and 4.If the spin-up(down)current injected into lead 1 transports along the red line,then the spin-down(up)current must follow the yellow line.

图6中设计了一个全新的六端系统来代替H形四端系统.图6和图3的惟一区别在于电极1和2的左端新添加了两个电极3′和4′,并使得它们与电极3和4呈镜面对称关系.现在,如果向电极1注入自旋向上极化的自旋流,例如通过引入铁磁电极的方法,一个非局域电压信号V34↑可以在电极3和4被探测到.此时的非局域电阻应写为

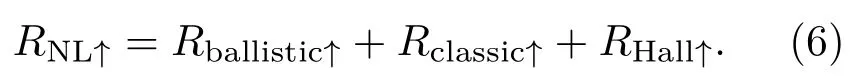
类似地,如果注入自旋向下极化的自旋流,可以探测到电压V34↓,且此时的非局域电阻可以写为

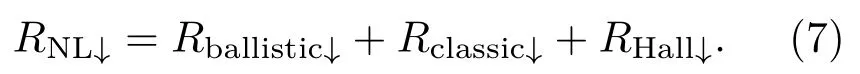
由于准弹道输运和经典扩散与自旋极化方向无关,这两种效应诱导的非局域电阻Rballistic和Rclassic在不同自旋方向下必相等,即Rballistic↑=Rballistic↓且Rclassic↑=Rclassic↓. 因此, 在得到RNL↑和RNL↓后,可以排除掉准弹道输运和经典扩散对结果的影响,并最终得到只由SHE诱导的非局域电阻:

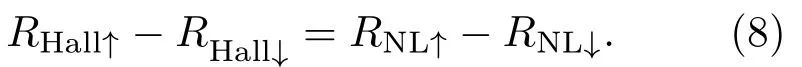
实际上,图6中六端系统最大的优点在于当自旋向上极化的自旋流从电极1入射时,除了电极34,电极3′4′端也可以测得电压根据对称性分析,应该等于在电极3,4测到的自旋向下电压V34↓. 因此,RHall↑−RHall↓可以通过一步测量得到而不需要改变电极1的磁化方向,这对于具体的实验操作而言至关重要.但对于理论计算,为了简单起见,依然选择使用两个自旋方向来讨论问题.

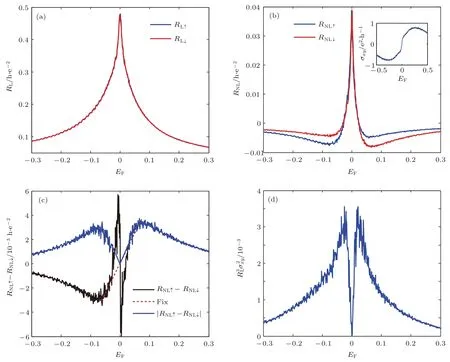
图7 对完全由SHE诱导的非局域电阻RHall的计算[18] (a)自旋向上和自旋向下对应的局域电阻RL;(b)自旋向上和自旋向下对应的非局域电阻RNL,内插图为自旋霍尔电导σxy;(c)黑线基于RNL↑−RNL↓计算得到,由于数值误差在EF=0处引发了剧烈的扰动,增加了一条红色虚线来准确地描述RNL↑−RNL↓,考虑红线的修正后,蓝线为黑线的绝对值RNL↑−RNL↓(d)基于(5)式计算的RHallFig.7.The nonlocal resistance RHallwhich is totally induced by the SHE[18].(a)The local resistance RLfor two spin direction.(b)The nonlocal resistance RNLfor two spin directions,and the inset is the spin Hall conductance σxy.(c)The black line is calculated based on RNL↑−RNL↓.Since the numerical error results in dramatic oscillation of RNL↑−RNL↓near EF=0,we add a red dad line to describe the accurate behavior of RNL↑−RNL↓near the Dirac point.At last,the blue line representsRNL↑−RNL↓which equals the absolute value of the black line.And the fi x near the Dirac pint shown by the red line is also considered.(d)RHallcalculated based on Eq.(5).

图7(a)首先展示了根据上述方法计算得到的局域电阻RL.由于局域电阻不依赖于霍尔效应而对自旋方向不敏感,所以两个极化方向完全相反的局域电阻表现出了几乎完全相同的行为.图7(b)给出了非局域电阻RNL↑和RNL↓.如图所示,蓝色的RNL↑和红色的RNL↓反对称.根据(5)式中对SHE的解释,这个反对称的现象可以由图6(b)内插图中自旋霍尔电导σxy的行为来理解.具体而言,由于σxy关于原点反对称[33]:σxy(EF)=−σxy(−EF),且σxy符号的改变实际上等价于SHE方向的改变.这意味着图7(b)中蓝线和红线的较小者(即EF＜0时的自旋向上和EF＞0时的自旋向下)可以被视为没有SHE的基准线,而较大者即为有SHE.因此,通过在EF＜0时从RNL↑中扣除RNL↓,并在EF＞0时从RNL↓中扣除RNL↑,可以得到完全由SHE诱导的非局域电阻:

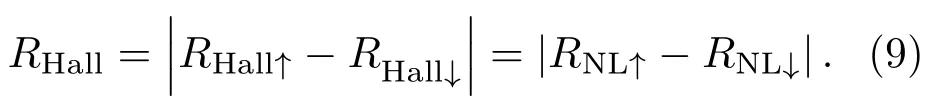
回到经典(5)式,由于它的原始推导实际上只考虑了霍尔效应,因此(5)式中的RNL理论上应该为RHall.在图7(c)中,首先给出基于RNL↑−RNL↓计算得到的非局域电阻RHall,其中EF=0附近的抖动主要源自数值误差.根据图7(b),σxy在EF=0处等于0,这意味着系统在狄拉克点处并不存在SHE.因此,RNL在EF=0时对自旋不敏感,即RNL↑必等于RNL↓. 也就是说,RNL↑ −RNL↓的准确值应该由图7(c)中的红色虚线表示,它连接两个峰值且通过原点.为了进一步验证结果,根据(5)式,在图7(d)中利用局域电阻RL和自旋霍尔电阻σxy重新计算了RHall,并将其与图7(c)中的RHall进行对比.如图所示,图7(c)和图7(d)的主要行为看起来完全相同,其中的细微区别可能是由于(5)式中的正比符号含有随费米面变化的参数.尤为重要的是,可以看到当EF等于0时RHall也等于0,这实际上意味着图4中非局域电阻RNL的尖锐峰与Rashba自旋轨道耦合完全无关.同时,更令人意外的是,这个结果还意味着非局域电阻RNL相比于局域电阻RL迅速衰减的性质同样不是由Rashba效应导致.不仅如此,如图7(c)和图7(d)所示,在EF=±0.1附近还存在一对由Rashba自旋轨道耦合导致的RHall峰值.显然,这对峰会随着Rashba效应的增强而愈发明显.现在,对于前文所述的关于图4的第三个特征,可以给出一个较完美的解释.如图4所示,非局域电阻的负数值部分同样出现在EF=±0.1附近,这恰好也是图7(c)中RHall峰值所在的位置.因此,这对RHall的峰值实际上对非局域电阻RNL的负值趋势起抵消作用,即表现为RNL相比RL的迅速衰减趋势随Rashba效应的增强而逐渐消失,也即决定非局域电阻RNL迅速衰减趋势的实际上是SHE与准弹道输运的竞争.

通过计算RHall和进一步的分析可知非局域电阻在狄拉克点表现出的巨大峰值的性质与Rashba效应无关.实际上,这个极大峰很有可能是由单层石墨烯在狄拉克点处的极小态密度导致的,这也意味着不能单纯地由非局域电阻峰值的出现来判断SHE的存在性.其次,非局域电阻相比于局域电阻迅速衰减的性质并不如之前所预料的那样由Rashba效应导致.现在,已清楚这个有趣的性质实际上是由准弹道输运诱导的非局域电阻Rballistic所导致.更重要的是,Rashba效应本身不仅没有诱导非局域电阻的迅速衰减,反而对这个迅速衰减的性质起到了某种屏蔽作用.

2.2 对由SHE诱导的非局域电阻组分的进一步分析

最新的研究细化了由SHE诱导的非局域电阻的组分,并重新验证了2.1节的结论[19].在(3)式的基础上,考虑内禀自旋轨道耦合和无序类型,系统的哈密顿量可以写为

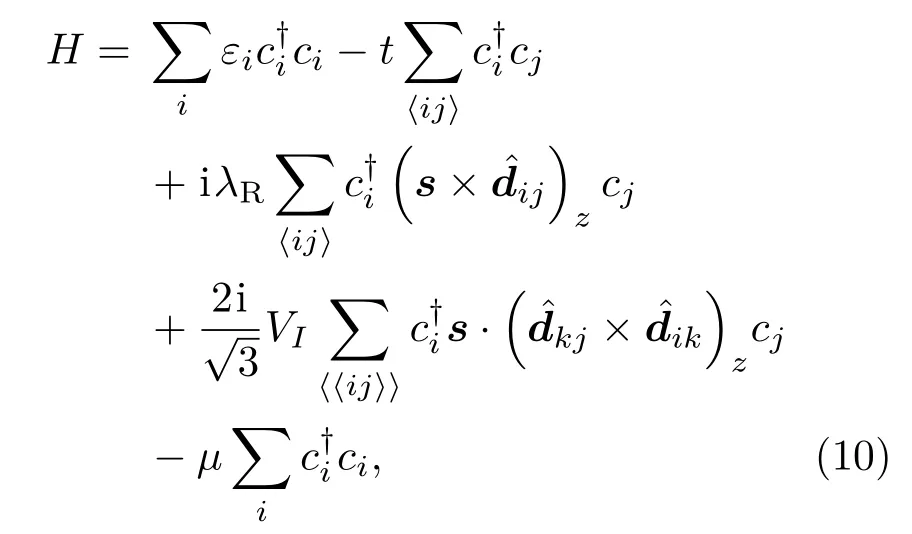
其中,第四项代表内禀自旋轨道耦合;最后一项是一个随机在位能,它被用来描述吸附原子带来的不同无序类型.

如图8(a)所示,首先考虑中心区完全纯净的石墨烯体系.经过Landauer-Buttiker公式的计算,图8(b)首先给出了固定宽度W时,非局域电阻RNL在不同长度L下随费米面的变化.如图8(b)所示,当W＞L时,非局域电阻RNL在狄拉克点表现出了一个巨大的峰值,这种行为类似于某种纯净石墨烯特有的欧姆电导输运.进一步地,当考虑金原子随机吸附带来(10)式中不为0的随机在位能µ0时,如图9(a)所示,即使此时所有的自旋轨道耦合项仍然被人为地取为0,依然可以观测到非局域电阻RNL的极大峰值.与2.1节中的分析相同,这个结果首先意味着实验中观测到的极大峰值实际上与SHE并无关系,同时暗示构成RNL的组合项除了(4)式中提及的三项,还应包含在狄拉克点附近产生的“准经典扩散”输运行为.这种输运机理源于此时的波函数可以穿透零能隙的狄拉克锥.同时,类似于图4,这里依然可以观测到一个负号的RNL.因此,作为对(4)式的细化,总的RNL应该考虑以下四项的贡献:

其中,Rballistic和RHall意义与(4)式相同.需要强调的是,Rclassic此时代表由于经典扩散造成的平庸欧姆贡献,而Rqd代表一个石墨烯特有的准扩散输运.

此外,如图9(a)中的两个插图所示,在不含自旋轨道耦合且L＞W的情况下,RNL表现出负值.这意味着在低吸附原子浓度的情况下,Rclassic可以被近似忽略.具体而言,由于在金原子吸附浓度nad=15%的情况下,自由程ℓ可估计为300—400 nm,所以在ℓ＜L的扩散输运区,欧姆贡献Rclassic∝exp(−πL/W)由于L/W≫1而可以完全忽略.也就是说,在L＞W时,非局域电阻的性质主要由负号Rballistic和正号RHall间的竞争所决定,这与2.1节中提出的推测符合.此外,从图9(a)的插图还可知,当L＞W时,非局域电阻RNL没有表现出极大峰值,即此时的Rqd可以忽略,这也与图8(b)的结论一致.图9(b)还给出了分散分布和团簇分布两种不同的吸附原子类型所对应的自旋霍尔角.显然,除了自旋轨道耦合项之外,吸附杂质的不同类型也会影响SHE的产生.同时,更高的温度也会降低自旋霍尔角.

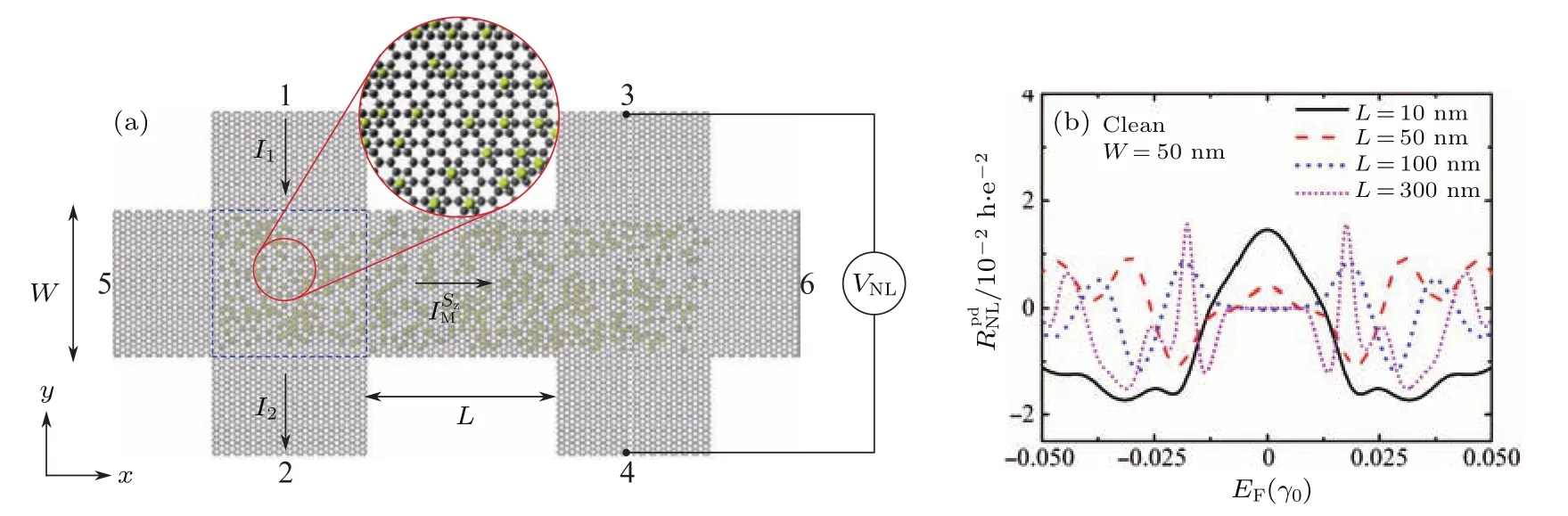
图8 (a)计算所使用的六端石墨烯示意图,非局域电阻RNL=VNL/I1,自旋霍尔角θsH=/I1,放大的插图描述了可能存在的无序杂质吸附;(b)当不存在无序时,基于纯净石墨烯计算的非局域电阻RNL及在固定宽度W=50 nm的情况下,RNL随样品长度L的变化[19]Fig.8.(a)The schematic diagram of a six-terminal graphene employed to compute the nonlocal resistance RNL=RNL/I1and the spin Hall angel θsH=/I1.The enlargement shows the possible adatoms.(b)The nonlocal resistance RNLcalculated in a perfectly clean graphene system,and how RNLvaries with the sample size L with a fi xed width W=50 nm[19].

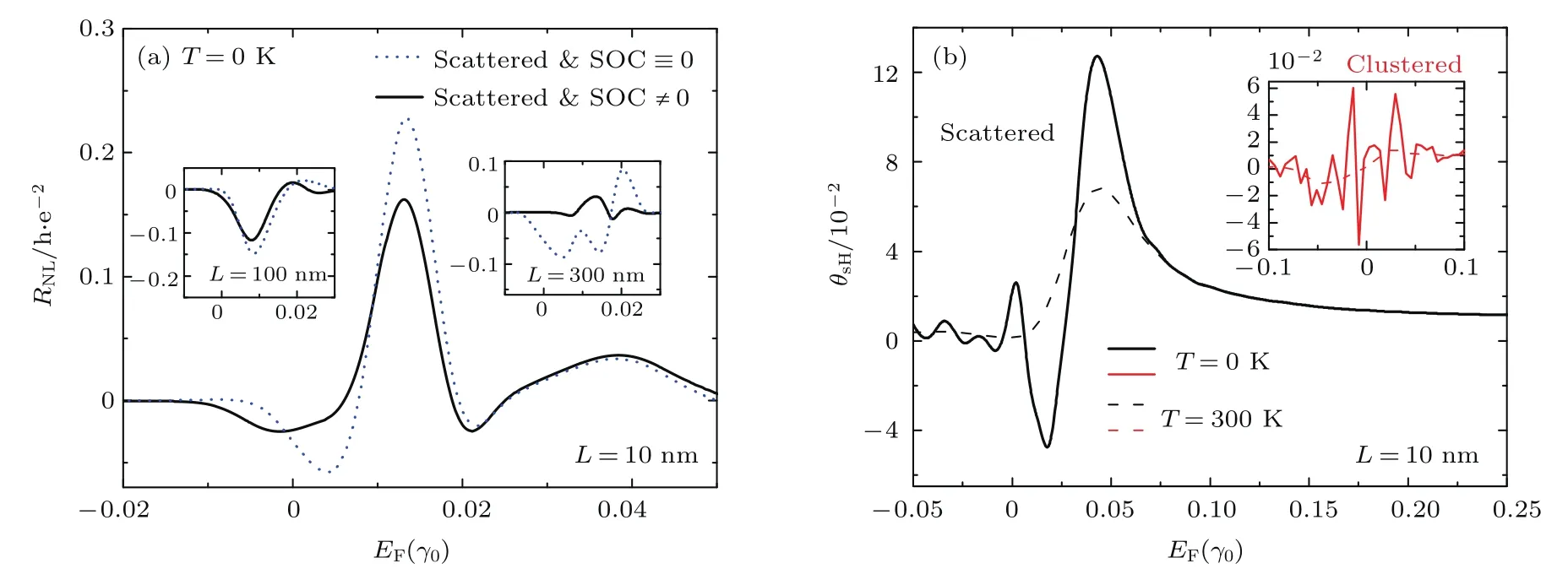
图9 (a)当取掺杂浓度nad=15%的均匀掺杂金原子时,固定宽度W=50 nm,非局域电阻RNL随不同样品长度的变化(L=10 nm(主图),L=100 nm(左插图),L=300 nm(右插图)),虚线代表(10)式中所有的自旋轨道耦合强度为0;(b)在相同的掺杂浓度下,不同掺杂种类对应的不同形态的自旋霍尔角[19]Fig.9.(a)The nonlocal resistance RNLcalculated based on Fig.8(a)with nad=15%of scattered Au atoms,fi xed channel width W=50 nm,and several channel lengths:L=10 nm(main frame),L=100 nm(left inset),L=300 nm(right inset).Dotted lines plot RNLwhen all SOC terms in Eq.(10)are swithed o ff.(b)The spin Hall angel for the same concentration of Au adatoms which are scattered or clustered[19].

通过上述分析,Tuan等[19]提出了一种新的排除Rballistic,Rclassic和Rqd,而只保留RHall影响的设计机理.相比于图8(a)的示意图,这个设计的变化在于:此时连接两个霍尔条的中心区不含杂质而由完全纯净的石墨烯组成,同时还要保证这个中心区的输运通道L足够长.此时,由于L＞W,Rqd和Rclassic等于0.同时,由于缺乏传输通道中的杂质散射,Rballistic也几乎趋于0.因此,这时图8(a)中的电中性自旋流完全起源于左侧霍尔条处的SHE,并在右侧霍尔条由ISHE转化为非局域电压VNL.相比于2.1节中分离RHall的六端装置,这个设计虽然物理正确,但由于其要求中心区完全纯净,在实际操作中并不现实.需要强调的是,基于这个设计得到的RHall同样在靠近狄拉克点的两侧表现出一对峰值,而在狄拉克点为0,这与图7(c)相符合.

事实上,尽管大量的实验和理论研究都观察到了非局域电阻RNL奇怪的负数性质,并推测其为准弹道输运行为的结果,但对于这个负数解,尚缺乏足够的证据进行有效的分析.例如,这个负数RNL究竟会在什么情况下出现.令人信服的工作需要依赖于如何能从RNL中分离出完全由准弹道输运诱导的非局域电阻Rballisitc,或者得到非局域电流的微观图像.值得注意的是,不同于小尺寸下利用Landauer-Buttiker公式的数值模拟,当尺寸达到扩散极限时,最新的研究通过解析求解自旋流所满足的连续性方程,在得到负数RNL的同时还给出了对这个负数解的不同理解[34].解析解的优势在于其可以计算出自旋轨道耦合的磁场长度ℓR和自旋弛豫长度ℓs.通过对二者进行比较,研究者提出由于自旋进动,RNL的负数值出现在当ℓR和ℓs大小可比时.尽管与之前的理论工作存在尺寸上的区别,但这也许会为人们理解非局域电阻RNL的负数行为提供一种新的思路.

3 ZSHE在石墨烯体系中诱导的非局域电阻

不同于SHE,石墨烯系统中的ZSHE不需要自旋轨道耦合,它是一种在外磁场作用下使得纵向电荷流转化为横向自旋流的现象[5,20−23].在垂直于面外的磁场作用下,如图10(a)所示,石墨烯的狄拉克锥由于塞曼相互作用而分裂.这意味着电子型和空穴型的载流子可以在CNP附近获得相反的自旋.

图10 ZSHE的非局域测量示意图[5] (a)CNP处的塞曼自旋劈裂导致电子和空穴拥有方向相反的自旋;(b)在洛伦兹力的作用下,电子和空穴感受到相反的作用力,电荷流I转化为自旋流I↑和I↓.由于这个大小不为0的自旋流IS=I↑−I↓可以传播相当远的距离,从而可以在远端测到一个非局域电压VNL;(c)非局域电阻RNL的实验值,在零磁场时,无非局域信号Fig.10.The schematic diagram for the nonlocal experiment of ZSHE[5].(a)Zeeman splitting at the CNP produces two pockets fi lled with electrons and holes having opposite spin.(b)In the presence of the Lorentz force,which has opposite signs for electrons and holes,I gives rise to transverse spin current I↑ and I↓.Since the nonzero spin current IS=I↑−I↓can reach remote regions,a nonlocal voltage VNLcan be detected.(c)The nonlocal conductivity RNLin experiment.There exists no nonlocal signal in zero magnetic field.

首先在外加垂直磁场的石墨烯系统中实验观测到了ZSHE诱导的非局域电阻[5].由于这个非局域信号的样品长度远大于传统欧姆信号的传播范围,因而其一定是由一个非平庸的机理所导致.起初,这一类由ZSHE所诱导的非局域信号被认为是由量子霍尔效应中的边缘态输运所导致.但实验发现,即使在室温(T=300 K)和极弱的外磁场(B≪1 T)等明显超出量子霍尔效应适用范围的情况下,非局域信号依然很明显.这意味着这种非局域特征是由完全不同于量子霍尔效应边缘态输运的机理所导致.此外,由于实验中使用的六角氮化硼衬底引入了电杂质和晶格畸变,这也排除了第2节中SHE所导致的RNL.因此,这个非局域电阻只能产生于ZSHE.

类似于SHE中非局域电阻的定义,在图10(b)中,自旋非极化的电流I从电极6向电极2入射.由于ZSHE,这个电荷流先转化为电中性的自旋流IS=I↑−I↓,然后在逆塞曼自旋霍尔效应的作用下被转换为可以在电极3和5探测到的非局域电压VNL=V5−V3.相对应地,非局域电阻的定义为RNL=VNL/I.

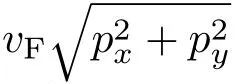
则速度

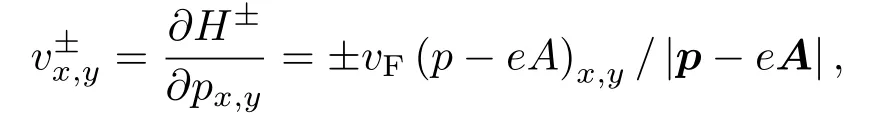
且加速度a为

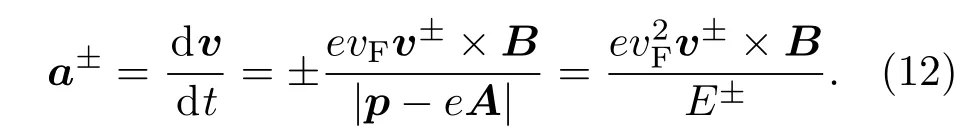
显然,能量E+和E−的准粒子在垂直磁场的作用下会感受到两个方向相反的洛伦兹力,并向相反的方向传播.不仅如此,尽管塞曼劈裂ΔZ通常很小,但在低温(kBT＜ΔZ)时,ΔZ可以在石墨烯中通过狄拉克锥的自旋退简并引入两种不同方向的自旋载流子.如图10(a)所示,能量E+的准粒子为自旋向上极化,而能量E−的准粒子为自旋向下极化.正是上述两种效应的叠加使得图10(b)中纵向传播的电荷流横向偏转为电中性的自旋流.

类似于SHE,含ZSHE的多端石墨烯体系同样可以通过Landauer-Buttiker公式给出一个全数值模拟[20].在CNP附近,石墨烯中外加磁场的紧束缚哈密顿量可以写为

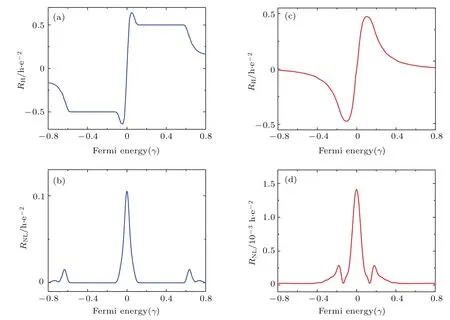
图11 在含ZSHE的六端系统中计算的电霍尔电阻RH和非局域电阻RNL[20](a)退相干较小时的RH;(b)退相干较小时的RNL;(c)退相干较大时的RH;(d)退相干较大时的RNLFig.11.The charge Hall resistance RHand the nonlocal resistance RNLcalculated based on the six-terminal graphene system with the ZSHE[20]:(a)RHwith a smaller momentum-relaxing dephasing;(b)RNLwith a smaller momentum-relaxing dephasing;(c)RHwith a larger momentum-relaxing dephasing;(d)RNLwith a larger momentum-relaxing dephasing.

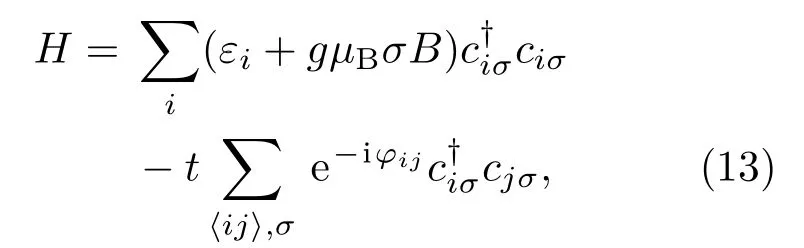
其中,εi是在位能;σ=±1对应于自旋向上下,即塞曼劈裂的大小为2gµBσB;t是最近邻跃迁项;φij是一个由于外磁场导致的跃迁相位.需要注意的是,接下来的计算中,由于样品放置在量子化外磁场中,磁长度ℓB和图10(b)中的输运通道宽度W的比值需要保持W/ℓB＞1.同时,由于非平衡格林函数计算的复杂性要求样品尺寸不能太大(计算中对于四端体系的宽度W≈2.7 nm,六端体系的宽度W≈2.0 nm),因此需要外加一个极大的磁场以保持W/ℓB＞1.

图11给出了在图10(b)所示的六端体系中使用Landauer-Buttiker公式的非平衡格林函数计算结果.在图11(b)中,非局域电阻RNL=(V5−V3)/I表现出了与实验图10(c)非常相似的结果:狄拉克点处巨大的非局域电阻峰值以及另一对CNP处的侧峰值.图11(d)相比于图11(b)增强了相位的退相干,此时的非局域电阻RNL在狄拉克点的峰值降低了两个数量级,同时两个侧峰也完全消失.

相比于SHE,ZSHE诱导的非局域电阻研究还缺乏足够深入的分析.例如,由于外磁场的存在,适用于SHE的分析并不完全适用于ZSHE.但ZSHE中的非局域电阻却有着与SHE类似的形态,那么这两类非局域电阻是否有着相同的组成,需要进一步的理论和实验探讨.

4 VHE在石墨烯体系中诱导的非局域电阻

在打破空间反演对称性的石墨烯中,谷自由度可以起到与自旋类似的作用[24].这意味着谷自由度也能够表现出对应的霍尔效应、磁化、光学选择定则甚至手性边缘态等现象.最近在MoS2等VI族过渡金属硫化物中的研究使人们对谷自由度的研究进一步深入[35−37].这类直接半导体材料的带隙正落在K点,同时其低能电子和空穴可以由带强自旋谷耦合的狄拉克费米子描述.因此,实验中往往同时观测到SHE和VHE.近年来,大量的研究试图通过电磁学方法来控制谷自由度,从而寻找可能的谷控制方法[38−40],并催生了谷电子学这门学科.

由于不同谷的电子带有相反的贝里相位,这使得通过谷产生谷依赖的输运成为可能.从一个半经典的角度考虑,上述输运现象起源于能带结构导致的反常群速度[41]:

其中,k是波矢,Ωn(k)是第n个能带的贝里相位,E是外电场.(14)式的最后一项代表了一个同时垂直于外电场和贝里相位的反常群速度.接下来考虑外加一个打破空间反演对称性的微扰,石墨烯打开能隙Δ,这时的狄拉克点附近的低能哈密顿量写为

则两个谷附近的贝里相位形式为

显然这里不同的谷分别对应两个相反的贝里相位.结合(14)式,此时两个谷感受到两个完全相反的类洛伦兹力,因而会向两个相反的方向传播,如图12所示.

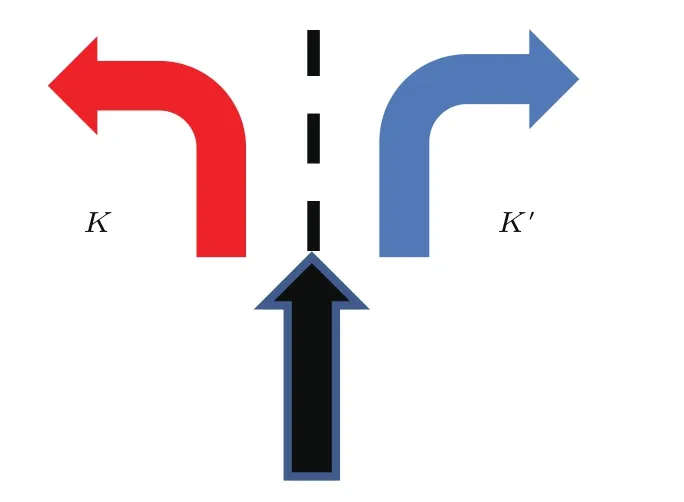
图12 由于贝里相位的作用,属于不同谷的电子会感受到两个完全相反的类洛伦兹力Fig.12.Due to the effect of Berry curvatures,the electrons in two different valleys will experience the Lorentz force in opposite directions.

从量子力学的角度而言,在K点附近,(15)式中的哈密顿量可以写为

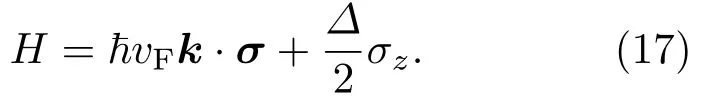
则此时的速度和加速度算符为

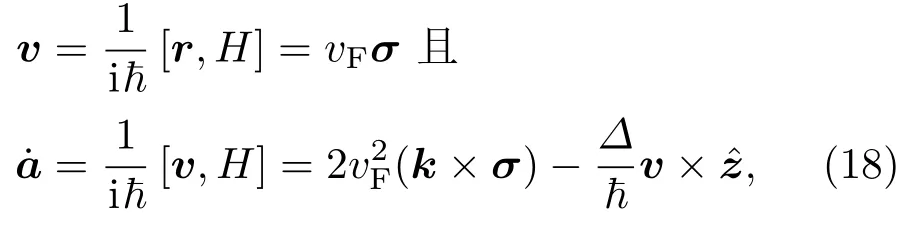
最近的实验首先在与六角硼化氮衬底公度的石墨烯样品中观测到了非局域电阻信号[7].如图13(a)和图13(b)所示,当石墨烯和硼化氮公度放置时,石墨烯的空间反演对称性被打破并在CNP打开能隙,此时样品表现出一个巨大的非局域电阻值RNL;而当石墨烯和硼化氮交错一个角度时,石墨烯保持空间反演对称性且不打开能隙,此时的非局域电阻值非常小,以至于几乎观测不到,这排除了源于SHE的自旋流可能对图13(a)中非局域电阻的贡献.同时,实验还认真地排除了边缘态等可能对非局域电阻的贡献.因此,一个合理的推测是这时的非局域信号可能源于由VHE诱导的谷电流.

图13 (a)在与六角硼化氮衬底公度的石墨烯样品中探测非局域电阻的示意图(插图)及非局域电阻RNL实验数据(主图);(b)实验中在公度与非公度情况下分别测量的非局域电阻RNL值[7]Fig.13.(a)The schematic diagram of the experimental device(inset)and the measured nonlocal resistance(main panel)for a multi-terminal graphene system aligned over an h-BN substrate;(b)experimental nonlocal resistance for aligned and non-aligned h-BN substrates[7].

更多的实验在外加垂直电场的双层石墨烯样品中同样观察到了巨大的非局域电阻[8,9].类似地,由于双层石墨烯此时也在CNP打开能隙,这个非局域电阻信号同样被倾向于理解为是VHE的结果.实际上,这类实验在理论上最难以理解的地方在于:所有的非局域电阻信号均出现在当费米能落在带隙中时,而这里本不应该存在任何物理的结果.Lensky等[25]认为这里的VHE可能起源于能隙以下的费米海体态.对于在带隙中的费米能EF,两个相反的谷极化流在系统中传播并产生电中性的谷电流.由于谷电流由能隙以下费米海中的电子传播,谷电流是非耗散的.因此,在这个图像中,即使系统表现为电绝缘且化学势落在带隙中,由费米海导致的谷电流仍然可以产生一个看起来违反直觉的非局域信号.针对这个观点,进一步的研究直接使用了参照图13中打开能隙且谷霍尔电导0的石墨烯哈密顿量,非平衡格林函数的计算结果表明非局域电阻RNL在带隙内永远为零.类似地,基于文献[8,9]中实验使用的双层哈密顿量的计算给出了同样的结果.最近,借助于第一性原理方法对哈密顿量的修正,Marmolejo-Tejada等[26]提出,这个非局域电阻应该是由某种特殊的出现在狄拉克点附近的边缘态所诱导,而并不是费米海体态.

图14 计算所使用的含子格子错位势Δ的四端石墨烯示意图Fig.14.The schematic diagram for the calculated four-terminal graphene system with a staggered sublattice potential Δ.

根据Landauer-Buttiker公式,Cresti等[42]在一个如图14所示的四端石墨烯中模拟了由VHE诱导的非局域电阻.此时,一个打破空间反演对称性的哈密顿量可以写为

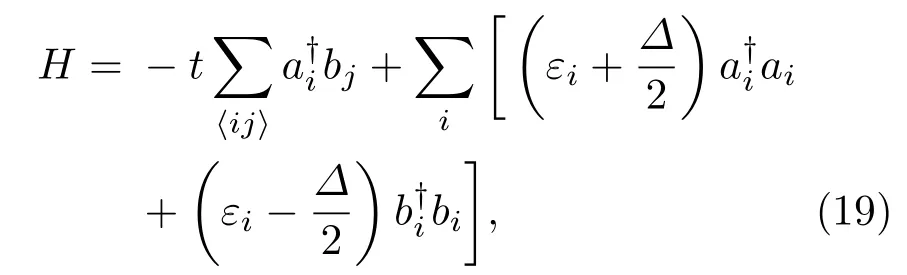
这里,ai和bi对应于两种子格子,并将宽度固定为W=50 nm.首先,当错位势Δ取为0时,石墨烯不打开能隙.相对应的计算结果显示,无论长度L如何取值,系统都不表现出可以被观测到的非局域电阻RNL.接下来,当错位势取为Δ=60.2 meV时,类似于实验现象,此时的石墨烯打开能隙Δ并在狄拉克点表现出一个巨大的非局域电阻峰值.显然,这个对比结果意味着基于(19)式得到的非局域电阻实际上源于VHE的贡献.更细致的计算表明,非局域电阻的峰值会随着长度L的减小而降低.这是由于能隙中的输运一般由能隙外的体态向能隙内的隧穿来实现,而隧穿概率会随着样品尺寸的增大而强烈地衰减.

综上所示,尽管目前并没有对谷电流直接测量的实验证据,但理论和实验研究都倾向于认为在打破空间反演对称性的石墨烯中观测到的巨大的非局域电阻值来源于VHE.更令人信服的结论还需要进一步深入的理论和数值计算.

5 结 论

本综述系统地回顾了实验上观测到的可能分别由SHE,ZSHE和VHE诱导的非局域电阻,并介绍了通过Landauer-Buttiker公式给出的上述三种霍尔效应在多端系统中诱导非局域电阻的全数值结果.对于SHE,理论计算较好地给出了符合实验现象的非局域电阻模拟值.同时,更细致的理论研究预言实验中观测到的非局域电阻峰值的产生很可能与SHE无关,而非局域电阻相比局域电阻的迅速衰减很可能源于SHE与准弹道输运的竞争关系.通过构造一个可以产生ZSHE和VHE的哈密顿量,也可以得到与实验结果符合较好的非局域电阻计算结果.但相比于SHE,对于ZSHE和VHE如何诱导非局域电阻的物理机理目前缺乏足够令人信服的结论.特别是对于VHE,非局域电阻出现在本不应该测到任何物理信号的体能隙中,这一直是一个令人费解的现象,并引发了激烈的争论.总体而言,尽管非局域电阻在近年来已经吸引了人们足够高的研究兴趣,但由于其非平庸的物理性质,对于非局域电阻仍需要更深入的理论研究和更直接的实验测量结果.

感谢中国北京大学陈剑豪教授、韩伟教授,美国特拉华大学Branislav K.Nikolic教授和中国台湾新竹清华大学Chunli Huang博士的讨论.

[1]Brune C,Buhmann H,Molenkamp L W,Maciejko J,Qi X L,Zhang S C 2009Science325 294

[2]Chang C Z,Zhao W,Kim K Y,Wei P,Jain J K,Liu C,Chan M H W,Moodera J S 2015Phys.Rev.Lett.115 057206

[3]Parameswaran S A,Grover T,Abanin D A,Pesin D A,Vishwanath A 2014Phys.Rev.X4 031035

[4]McEuen P L,Szafer A,Richter C A,Alphenaar B W,Jain J K,Stone A D,Wheeler R G,Sacks R N 1990Phys.Rev.Lett.64 2062

[5]Abanin D A,Morozov S V,Ponomarenko L A,Gorbachev R V,Mayorov A S,Katsnelson M I,Watanabe K,Taniguchi T,Novoselov K S,Levitov L S,Geim A K 2011Science332 328

[6]Balakroshnan J,Koon G K W,Jaiswal M,Castro Neto A H,Ozyilmaz B 2013Nat.Phys.9 284

[7]Gorbachev R V,Song J C W,Yu G L,Kretinin A V,Withers F,Cao Y,Mishchenko A,Grigoreiva I V,Novoselov K S,Levitov L S,Geim A K 2014Science346 448

[8]Shimazaki Y,Yamamoto M,Borzenets I V,Watanabe K,Taniguchi T,Tarucha S 2015Nat.Phys.11 1032

[9]Sui M,Chen G,Ma L,Shan W Y,Tian D,Watanabe K,Taniguchi T,Jin X,Yao W,Xiao D,Zhang Y 2015Nat.Phys.11 1027

[10]Yamamoto M,Shimazaki Y,Borzenets I V,Tarucha S 2015J.Phys.Soc.Jpn.84 121006

[11]Hirsch J E 1999Phys.Rev.Lett.83 1834

[12]Murakami S,Nagaosa N,Zhang S C 2003Science301 1348

[13]Sinova J,Culcer D,Niu Q,Sinitsyn N A,Jungwirth T,MacDonald A H 2004Phys.Rev.Lett.92 126603

[14]Kato Y K,Myers R C,Gossard A C,Awsschalom D D 2004Science306 1910

[15]Kimura T,Otani Y 2007Phys.Rev.Lett.99 196604

[16]Brune C,Roth A,Novik E G,Konig M,Buhmann H,Hankiewicz E M,Hanke W,Sinova J,Molenkamp L W 2010Nat.Phys.6 448

[17]Sheng L,Sheng D N,Ting C S,Haldane F D M 2005Phys.Rev.Lett.95 136602

[18]Wang Z,Liu H,Jiang H,Xie X C 2016Phys.Rev.B94 035409

[19]Tuan D V,Marmolejo-Tejada J M,Waiintal X,Nikolic B K,Valenzuela S O,Roche S 2016Phys.Rev.Lett.117 176602

[20]Chen C L,Chang C R,Nikolic B K 2012Phys.Rev.B85 155414

[21]Renard J,Studer M,Folk J A 2014Phys.Rev.Lett.112 116601

[22]Wei P,Lee S,Lemaitre F,Pinel L,Cutaia D,Cha W,Katmis F,Zhu Y,Heiman D,Hone J,Moodera J S,Chen C T 2016Nat.Mater.15 711

[23]Abanin D A,Gorbachev R V,Novoselov K S,Geim A K,Levitov L S 2011Phys.Rev.Lett.107 096601

[24]Xiao D,Yao W,Niu Q 2007Phys.Rev.Lett.99 236809

[25]Lensky Y D,Song J C W,Samutpraphoot P,Levitov L S 2015Phys.Rev.Lett.114 256601

[26]Marmolejo-Tejada J M,Garcia J H,Chang P H,Sheng X L,Cresti A,Roche S,Nikolic B K 2017 arXiv:1706.09361v1[cond-mat.mes-hall]

[27]Saitoh E,Ueda M,Miyajima H,Tatara G 2006Appl.Phys.Lett.88 182509

[28]Valenzuela S O,Tinkham M 2006Nature442 176

[29]Kimura T,Otani Y,Sato T,Takahashi S,Maekawa S 2007Phys.Rev.Lett.98 156601

[30]Balakrishnan J,Koon G K W,Avsar A,Ho Y,Lee J H,Jaiswal M,Baeck S,Ahn J,Ferreira A,Cazalilla M A,Castro Neto A H,Ozyilmaz B 2014Nat.Commun.5 4748

[31]Abanin D A,Shytov A V,Levitov L S,Halperin B I 2009Phys.Rev.B79 035304

[32]Mihajlovic G,Pearson J E,Garcia M A,Bader S D,Ho ff mann A 2009Phys.Rev.Lett.103 166601

[33]Sheng L,Sheng D N,Ting C S 2005Phys.Rev.Lett.94 016602

[34]Huang C,Chong Y D,Cazalilla M A 2017Phys.Rev.Lett.119 136804

[35]Mak K F,McGill K L,Park J,McEuen P L 2014Science344 1489

[36]Lee J,Mak K F,Shan J 2016Nat.Nanotechnol.11 421

[37]Xiao D,Liu G B,Feng W X,Xu X D,Yao W 2012Phys.Rev.Lett.108 196802

[38]Zhai F,Zhao X,Chang K,Xu H Q 2010Phys.Rev.B82 115442

[39]Gunlycke D,White C T 2011Phys.Rev.Lett.106 136806

[40]Zhai F,Ma Y L,Chang K 2011New J.Phys.13 083029

[41]Xiao D,Chang M C,Niu Q 2010Rev.Mod.Phys.82 1959

[42]Cresti A,Nikolic B K,Garcia J H,Roche S 2016La Rivista Del Nuovo Cimento12 587

PACS:72.80.Vp,71.70.Ej,85.35.–p DOI:10.7498/aps.66.217201

*Project supported by the National Basic Research Program of China(Grant Nos.2015CB921102,2014CB920901),the National Natural Science Foundation of China(Grant Nos.11704348,11374219,11534001,11404300),and the Science Challenge Project,China(Grant No.TZ2016003-1).

†Corresponding author.E-mail:jianghuaphy@suda.edu.cnc

Nonlocal resistance in multi-terminal graphene system∗

Wang Zi-Bo1)2)Jiang Hua3)4)†Xie Xin-Cheng5)6)

1)(Microsystems and Terahertz Research Center,China Academy of Engineering Physics,Chengdu 610200,China)
2)(Institute of Electronic Engineering,China Academy of Engineering Physics,Mianyang 621999,China)
3)(College of Physics,Optoelectronics and Energy,Soochow University,Suzhou 215006,China)
4)(Institute for Advanced Study of Soochow University,Suzhou 215006,China)
5)(International Center for Quantum Materials,School of Physics,Peking University,Beijing 100871,China)
6)(Collaborative Innovation Center of Quantum Matter,Beijing 100871,China)

d 21 September 2017;revised manuscript

7 October 2017)

Since the nonlocal measurement is helpful in discovering nontrivial physics that is too difficult to detect directly,the nonlocal measurement has now become one of the research focuses in condensed matter physics.Recent experiments find the signal of the giant nonlocal resistance in an H-shaped multi-terminal graphene system.After excluding other possible transport mechanisms,such as the classic Ohmic diffusion and the edge states,researchers tend to believe that the nonlocal resistance signal originates from the spin/valley Hall effect existing in graphene sample.Based on the Landauer-Buttiker formula,the numerical results make a relatively perfect match with the experimental data in the same multi-terminal graphene system.However,though the theoretic research has made certain progress in explaining the existence of the nonlocal resistance,it is still difficult to understand some exotic behaviors of the nonlocal resistance,which exhibits properties even contradictory to the known classical theories.For instance,the nonlocal resistance decreases to zero much more rapidly than the local one,and the giant peak of the nonlocal resistance appears inside the energy gap of the graphene.In this review,the experiments focusing on the nonlocal resistance in multi-terminal graphene system are carefully reviewed.Besides,this review also shows the associated theoretic studies,and an overlook of the future study is also provided.

nonlocal resistance,graphene,spin Hall effect,valley Hall effect

非局域测量方法由于其能够间接探测某些难以直接俘获的非平庸物理机理,近年来已逐渐成为凝聚态物理的研究热点之一.最近的实验在H形多端口石墨烯样品中发现了巨大的非局域电阻信号.在排除了经典欧姆、边缘态等可能的输运形式后,人们倾向于认为这类非局域电阻是由多端石墨烯系统中存在的自旋霍尔效益或谷霍尔效应所导致.借助于非平衡格林函数输运计算,目前的理论可以在同样的多端石墨烯体系中得到部分与实验符合较好的数值模拟结果.针对实验中发现的某些难以理解的、甚至与经典理论相矛盾的非局域电阻性质,例如非局域电阻相比局域电阻在偏离电中性点时的迅速衰减、出现在能隙中的非局域电阻峰值等,目前的理论研究取得了一定的进展,但对这些奇异现象的理解仍存在较大的争议.本综述详细回顾了多端口石墨烯体系中非局域电阻的相关实验,并针对性地介绍与之配套的理论进展及对未来研究的展望.

10.7498/aps.66.217201

∗国家重点基础研究发展计划(批准号:2015CB921102,2014CB920901)、国家自然科学基金(批准号:11704348,11374219,11534001,11404300)和科学挑战计划(批准号:TZ2016003-1)资助的课题.

†通信作者.E-mail:jianghuaphy@suda.edu.cnc

©2017中国物理学会Chinese Physical Society