考虑负载率均衡及风险成本的变电站规划

王思莹 常 俊 李 永 赵殿平 李 磊



考虑负载率均衡及风险成本的变电站规划

王思莹1常 俊2李 永3赵殿平1李 磊1

（1. 东北电力大学电气工程学院，吉林吉林 132012; 2. 国网沈阳供电公司，沈阳 110000;3. 国网河南民权县供电公司，河南民权 476800）

负载率均衡和风险成本是对变电站规划结果在实际应用中适应性的直接反应。建立了变电站规划数学模型，提出了考虑负载率均衡和风险成本的变电站规划方法。该方法将负载率均衡用熵值来处理，在风险理论的基础上，建立设备、变电站及线路风险成本模型，同时反应了规划结果的经济性和合理性，结合K-means算法对该模型进行有效求解。算例分析验证了所提规划方法的合理性与传统规划方法相比，采用所提方法规划结果更加合理。

变电站规划；负载率均衡；风险成本；熵值；K-means算法

配电网变电站作为电力系统的重要一环，是连接不同电压等级的枢纽点，其规划的合理性直接影响着系统的网络结构、供电可靠性及运行经济性。

文献[1-3]分析了不利地形、行政区域等实际因素对配电网变电站选址、定容及供电区域规划结果的影响，建立了相应的变电站规划模型。文献[4]从供电能力的角度对配电网变电站进行了规划。文献[5]在传统配电网变电站规划模型的基础上，考虑了变电站本身运行产生的损耗费用、故障产生的停电损失费用，并利用混沌迁移知识的差分文化算法实现对模型的求解。文献[6-8]不仅讨论了初始建设成本，同时考虑了其运行维护成本、废弃成本等，即利用全寿命周期理论（LCC）对配电网变电站的规划进行建模。文献[9-11]将负荷、电价和土地价格的不确定性作为风险成本，建立基于LCC理论的经济性最优的配电网变电站规划模型。

目前在配电网变电站规划课题研究中，多为对于外在环境对规划结果的影响，如地理因素、不确定性等，针对变电站规划时设备及线路本身的故障风险讨论不足。对此，本文基于熵理论，通过对各变电站负载率分析反应负荷分布均衡程度，将设备风险、变电站风险及线路风险分别予以量化并转为经济性指标，结合两者建立了考虑负载率均衡和风险成本的变电站规划模型，使得方案在满足经济性与可靠性的同时更符合实际情况，最终利用K-means算法实现对该模型进行有效求解。

1 变电站规划模型的建立

1.1 基于熵理论的负载率均衡评估

在进行变电站规划时，一般以规划区域负荷预测结果、负荷类型、现有变电站构成情况及容载比要求作为根据，通常忽略了对各变电站负载率的要求，使得负荷在各变电站上分配不均，变电站出现重载或轻载的现象。由于负荷的地理分布在规划前就已确定，故可以通过规划变电站位置及供电范围，解决变电站负载率不均衡的问题。在不超过变电站容量、满足负荷需要的情况下，尽可能使变电站的负载率均衡，避免变电站出现重载或轻载的情况，提升配电网供电能力。

信息熵是对事物不确定性的量化，其数值的大小即反应事物不确定性的大小。在评估变电站负载率指标时，指标离散程度越小，其分布的信息熵越小，也就是说，信息熵可以作为负载率分布均衡度的量度[12-13]。

以单个变电站负载率e占系统所有变电站负载率和的大小表征变电站的重要度I，有

根据熵理论，构建变电站负载率熵，即

由上式可知，当变电站负载率相等时，熵值达到最小，即min=1/ln。其中为变电站总座数。

1.2 建立风险成本模型

在工程应用中，国内外学者普遍接收的风险定义是：“风险是指人类从事某种活动时，在一定时期内可能会发生的具有损失性后果事件的危害，这种危害来自于两个方面，即可能性（概率）和严重性（后果），而风险值就是二者的乘积，即=×”[14-15]。

为建立经济性最优的变电站规划模型，本文从停电损失角度对变电站规划风险进行评估。由于停电损失与变电站容量、负荷类型、停电发生和持续时间等因素有关，建立风险成本评估模型如下：

式中，为风险成本；为失效事件发生的概率；为故障的经济后果严重度指标。

1）设备风险成本

（1）元件失效发生的概率P

（2）故障的经济后果严重度S

首先，需统计在不同停电持续时间时，系统处于最大负荷下的总停电损失，将得到的总停电损失与总最大负荷做商，得到平均用户停电损失模型，即各类用户停电损失函数SCDF()。本文通过经验，取SCDF()见表1[17]，可得到各类用户停电损失和停电持续时间的关系。

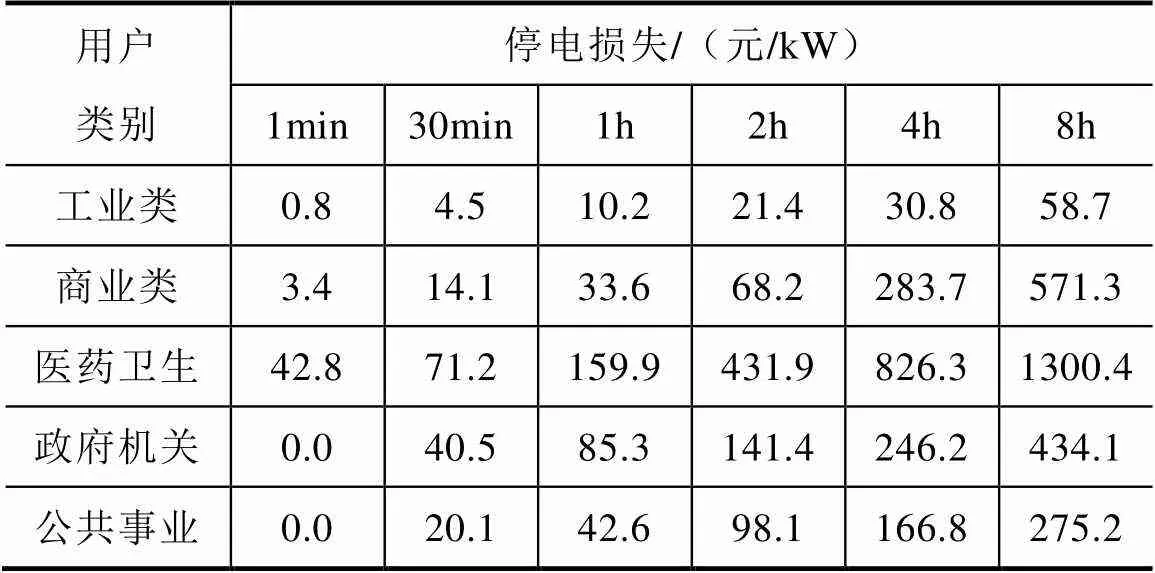
表1 各类用户停电损失

当各故障的持续时间在表中无直接对应的时间时，其停电损失可由表1中相邻的故障时间的线性插值计算得到。

其次，在建立的SCDF()基础上，结合各类用户的用电量比例和负荷率，可以能得到说明综合停电损失和停电时间的关系的综合停电损失函数CCDF()，即

式中，为第类负荷；为用户的类别数；c为第类用户的用电量比例，SCDF()为第类用户的停电损失函数，L为第类用户的负荷率。

最后，结合设备所带负荷大小S建立故障的经济后果严重度模型，即

由上述可得设备风险成本为

2）变电站风险成本

假设断路器、熔断器、隔离开关100%可靠，即不考虑其故障率，当变压器发生故障时，若此变电站无备用容量或另一台变压器容量不够，所切负荷的停电时间等于变电站的修复时间，则修复时间可由变电站的修复率求得。

变电站故障的经济后果严重度S=CCDF()×S，S为该变压器所带所有负荷。

变压器风险成本指标R=P×S。

3）线路风险成本

线路故障的经济后果严重度为

S=fCCDF()×S（7）

式中，S为该线路所带所有负荷。

线路风险成本

R=P×SFj（8）

所有线路风险成本

1.3 建立变电站规划模型

式中，substation为变电站投资及运行费用；line馈线投资费用和年网损费用之和；为网损折算系数；W为线路所带有功负荷，(S)为变电站的负载率；l为第座变电站到第个负荷的距离，为变电站负载率熵，cos为第座变电站功率因数。

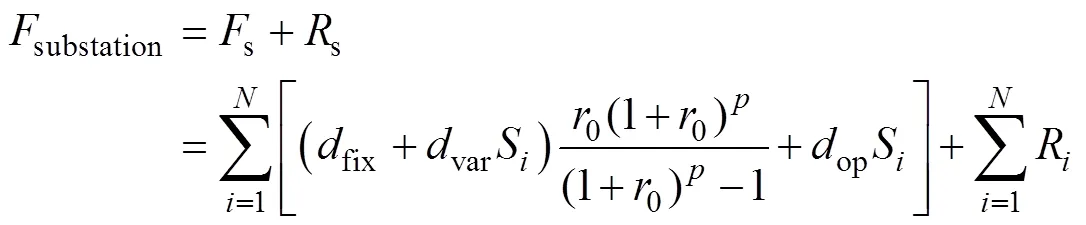
需要说明的是，在进行实际变电站规划时，应首先由负荷的大小、位置及类型分别选取适当的变电站容量，然后在得到变电站容量的基础上根据该区域的容载比确定变电站个数，最后，根据本文所建立的变电站规划模型确定变电站的位置和供区范围。当变电站容量选取出现多个备选方案时，可分情况讨论每种容量方案下利用本模型确定的规划结果，再对比不同情况下的规划结果，以经济性最优确定最终规划方案。

2 基于K-means算法的模型求解

2.1 K-means算法基本原理

K-means算法是基于划分的聚类算法，这类算法将数据集归为不同簇内，各簇间相似度低且互不相交，各簇内相似度较高。

其基本思想是：首先将数据集归为个不同簇，且人为或任意选择各簇中的一个对象作为该簇中心点；在建立准则函数的基础上，为达到最大程度降低函数值的目的，对各簇中的数据进行重新分配，并更新此时各簇的中心点；重复以上步骤直至各簇中心点不再变化为止。需要注意的是，在迭代过程中，进行数据重新分配时，应遵循距离就近原则，将数据对象分配给最近的那个中心点所在的簇，从而使得准则函数的值逐渐减小，实现快速收敛[18]。

K-means准则函数为

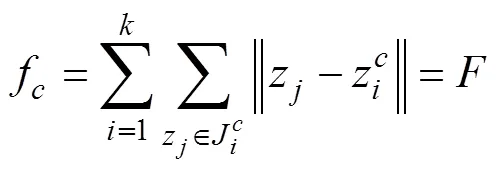
2.2 初始聚类中心的选择

为加快收敛速度得到较好的规划结果，本文利用最大最小距离法确定初始聚类中心。首先，根据数据对象情况设定一密度参数，将数据实际分布情况与该参数进行对比，可以得到一高密度区域，其中的数据对象构成一高密度点集合。其次，对中所有数据对象进行分析，取处于最高密度的数据对象作为第1个聚类中心1，在此基础上，取距离1最远的另一个高密度点作为第2个聚类中心2。

为求取第3个聚类中心，定义中数据对象X到1、2的距离为(X,1)和(X,2)，在本文中，即为两数据对象在地理位置上的距离。将满足max(min((X,1)), min((i,2)))的数据对象作为3，以此类推,找到个初始聚类中心。

2.3 应用

对变电站规划来说，规划区域之前可能已经存在部分变电站，此时，确实初始聚类中心时，先选择已建成变电站作为初始聚类中心（1～），其他（）个初始聚类中心利用最大最小距离法进行选择，同时，在进行聚类时，（1～）聚类中心位置不变，即聚类位置不更新，一直为初始聚类中心。其他聚类中心位置不断更新。

在本文中，以变电站规划费用作为准则函数。求解基本流程如图1所示。

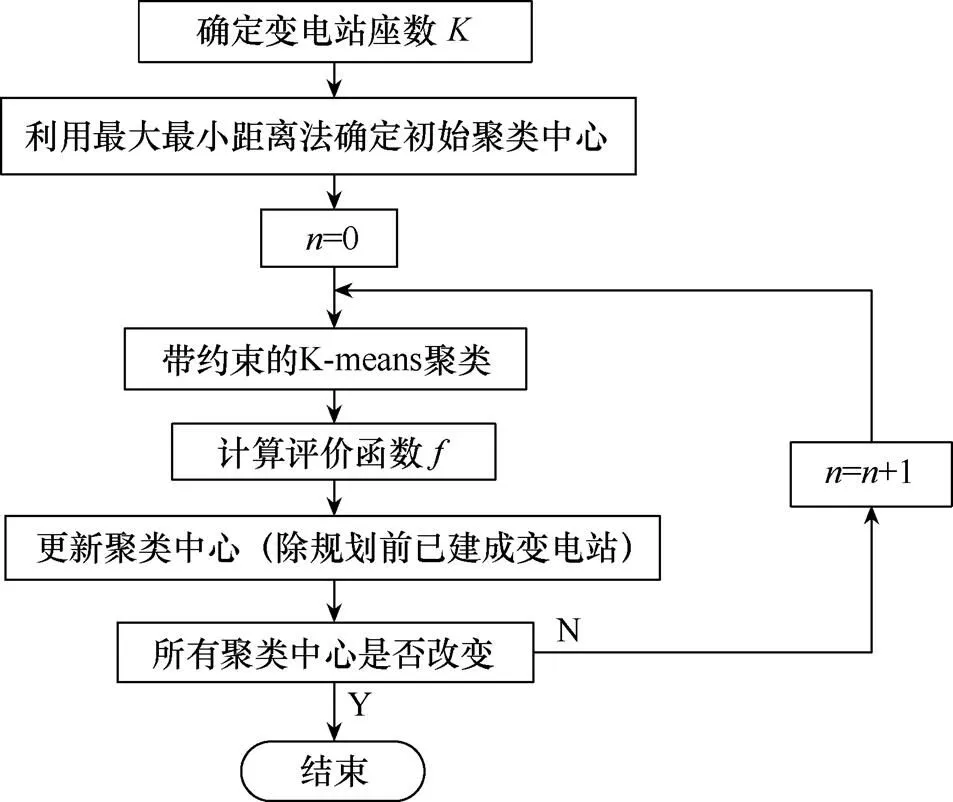
图1 变电站规划K-means算法流程图

3 算例分析

本文引用文献[1]算例对前文建立的模型进行验证。规划区域负荷分布如图2所示。

图2 规划区域负荷分布

若规划区域选取2×50MVA作为变电站的容量，则该地区需要4座变电站，是否考虑负载率均衡的规划结果分别如图3、图4所示。

在不考虑负载率均衡的情况下，计算得到变电站成本为4672.8万元，其中风险成本为893.3万元，各变电站负载率见表2，负载率熵为0.7868。

图3 未考虑负载率均衡的变电站规划方案

表2 未考虑负载率均衡的变电站规划结果

图4 考虑负载率均衡的变电站规划方案

在考虑负载率均衡的情况下，计算得到变电站成本为4535.7万元，其中风险成本为926.5万元，各变电站负载率见表3，负载率熵为0.6723。

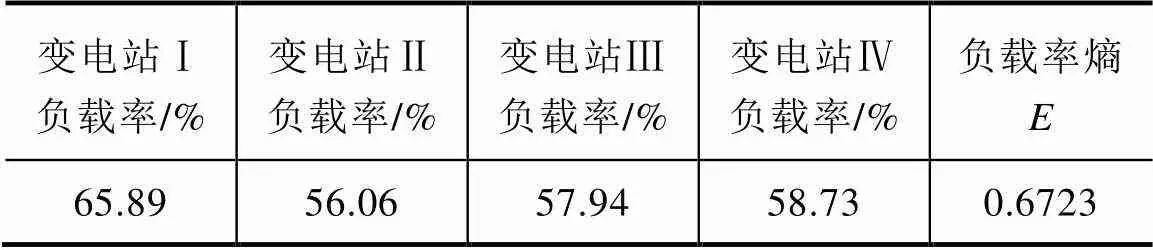
表3 考虑负载率均衡的变电站规划结果

对比图3和图4并结合表2和表3可知，考虑负载率均衡进行变电站规划时，所得最优规划方案风险成本较未考虑负载率均衡进行变电站规划所得的最优规划成本有所增加，但由于负载率熵有较大幅度的下降，使得最终计算所得变电站规划成本有所降低，即图4所示规划方案优于图3所示规划方案方案。

4 结论

本文建立了考虑负载率均衡和风险成本的变电站优化规划的数学模型，并利用K-means算法对模型进行求解。规划模型不仅包括变电站和线路的投资和运行费用，还计及了设备风险成本、变电站风险成绩线路风险成本，将负载率均衡度以熵的形式引入成本模型中。由前文可以得出，考虑负载率均衡的变电站规划方案风险成本比不考虑负载率均衡的情况略高，但是从实际运行角度来看，规划结果更加合理，负荷分布更均匀，不会出现变电站重载或轻载的现象，符合实际需求。利用本文提出的变电站规划方法可以对配电网变电站进行合理的规划，满足工程需求，为后续的配电网规划工作打下基础。

目前分布式电源在配电网中的渗透率越来越高，研究其对配电网变电站规划的影响也变得十分必要，涉及潮流多向流动以及优化目标更为复杂，将作为后续主要研究内容。

[1] 符杨, 卫春峰, 李振坤, 等. 考虑地理信息和行政边界的变电站供区优化[J]. 电网技术, 2014, 38(1): 3728-3733.

[2] 陶青松, 肖峻, 王笑一. 基于地理信息的变电站选址定容模型与算法[J]. 电力系统及其自动化学报, 2010, 22(6): 32-37.

[3] 王成山, 魏海洋, 肖峻, 等. 变电站选址定容两阶段优化规划方法[J]. 电力系统自动化, 2005, 29(4): 62-66.

[4] 于明, 郭华, 潘珍, 等. 基于提升供电能力的配电网协调规划探析[J]. 电气技术, 2015, 16(10): 107-110.

[5] 汪臻, 盛四清, 周庆捷. 不确定环境下配电网变电站选址定容[J]. 电力建设, 2014, 35(3): 59-63.

[6] 苏海锋, 张建华, 梁志瑞, 等. 基于全寿命周期成本的配电网变电站选址定容优化规划[J]. 电力系统自动化, 2012, 36(23): 59-64.

[7] 苏海锋, 张建华, 梁志瑞, 等. 基于GIS空间分析与改进粒子群算法的变电站全寿命周期成本规划[J]. 中国电机工程学报, 2012, 32(16): 92-99.

[8] 苏海锋, 张建华, 梁志瑞, 等. 基于改进均值聚类随机粒子群算法的变电站LCC规划[J]. 电工技术学报, 2012, 27(4): 209-215.

[9] 姜小静, 苏海锋, 梁志瑞. 计及风险成本的配电网变电站规划方法[J]. 电力自动化设备, 2014, 34(6): 141-145, 167.

[10] 闫丽梅, 许爱华, 任爽, 等. 一种变电站选址的新方法[J]. 高电压技术, 2007, 33(9): 75-79.

[11] 何永秀, 罗涛, 方锐. 基于风险分析的变电站选址优化研究[J]. 华北电力大学学报, 2011, 38(3): 53-57, 66.

[12] 张炳达, 王静. 基于熵原理的电能质量评估新方法[J]. 电力自动化设备, 2009, 29(10): 35-38.

[13] 丁明, 过羿, 张晶晶, 等. 基于效用风险熵权模糊综合评判的复杂电网节点脆弱性评估[J]. 电工技术学报, 2015, 30(3): 214-223.

[14] (加)李文沅, 周家启[等]译. 电力系统风险评估模型、方法和应用[M]. 北京: 科学出版社, 2006.

[15] 刘秋华, 董丹丹, 韩韬. 基于层次分析法的配电网风险评估指标体系研究[J]. 电气技术, 2016, 17(9): 39-42.

[16] 王璁, 李晓, 屠幼萍. 变压器质量风险的全寿命周期评估方法研究[J]. 电气技术, 2014, 15(5): 31-34, 43.

[17]周莉梅, 范明天. 城市电网用户停电损失估算及评价方法研究[J]. 中国电力, 2006, 39(7): 70-73.

[18] 苑津莎, 张利伟, 李中, 等. 基于互补免疫算法的变压器故障诊断[J]. 电工技术学报, 2015, 30(24): 67-75.

Distribution Substation Planning Considering Balance of Load Rate and Risk Cost

Wang Siying1Chang Jun2Li Yong3Zhao Dianping1Li Lei1

(1. School of Electrical Engineering, Northeast Electric Power University, Jilin, Jilin 132012;2. State Grid Shenyang Power Supply Company, Shenyang 110000;3. State Grid Minquan Power Supply Company, Minquan, He’nan 476800)

Balance of load rate and risk cost are direct responses to the adaptability of substation planning results in practical applications. The mathematical model of substation planning is established, and the substation planning method considering load balancing and risk cost is put forward. Based on the risk theory, this paper establishes the cost model of equipment, substation and line, and reflects the economics and rationality of the planning result. The K-Means algorithm is used to analyze the model. The result of the case shows that the rationality of the proposed method is more reasonable than that of the traditional planning method.

substation planning; balance of load rate; risk cost; entropy; K-means algorithm

王思莹（1992-），女，河北保定人，硕士研究生，主要研究方向为配电网规划及风险评估。