盾构隧道开挖面涌水对地表沉降及管片内力的影响分析

叶 治， 刘华北， 刘 文

(华中科技大学土木工程与力学学院， 湖北 武汉 430074)

盾构隧道开挖面涌水对地表沉降及管片内力的影响分析

叶 治， 刘华北， 刘 文*

(华中科技大学土木工程与力学学院， 湖北 武汉 430074)

土压平衡盾构在高水压砂层中掘进时，施工措施不当会使开挖面发生涌水涌砂险情，进而引起较大的地表沉降，土体下沉会使得管片严重变形，威胁施工人员的生命安全。以武汉地铁7号线小东门至武昌火车站盾构区间为研究背景，通过建立精细化数值模型，考虑水土流固耦合作用，研究土压平衡盾构在砂土层中掘进时开挖面涌水对地表沉降及管片和螺栓内力的影响。结果表明： 开挖面涌水量与地表沉降呈线性关系，与管片螺栓内力呈非线性增长关系，较大的涌水量使隧道拱顶处发生严重的挤压变形，进而引起管片破损及螺栓屈服。因此，当开挖面发生涌水涌砂险情时，为防止地表严重下沉及管片破损，应尽快采取紧急措施减小涌水量。

盾构隧道； 土压平衡盾构； 流固耦合； 数值模拟； 开挖面涌水涌砂； 地表沉降； 管片内力； 螺栓内力

0 引言

与泥水盾构相比，土压平衡盾构具有掘进速度快、附属设施简单的优点，逐渐成为城市地铁建设的首选。城市依山傍水而生，当土压盾构在高水压粉细砂层中掘进时，极易发生开挖面涌水失稳，因此，控制开挖面水头对于控制地表沉降及开挖面稳定至关重要。当下穿重要建筑物时，应严格控制开挖面排水量，防止开挖面出现涌水涌砂，从而有效保证盾构隧道的施工安全。

很多学者从工程实践技术和数值模型的角度研究了土压平衡盾构在高水压粉细砂层施工过程中的灾害风险及应对措施。朱自鹏[1]研究了土压平衡盾构在砂卵石地层掘进时的防喷涌技术，通过渣土改良技术来防止隧道开挖面的喷涌； 张远荣[2]利用FLAC3D模拟土压平衡盾构隧道，研究了盾构经过富水砂层时对周围环境的影响； 朱玉龙等[3]对土压平衡盾构下穿河道的受力特性进行模拟研究，但未考虑水土流固耦合的作用，忽略了开挖面水力边界的影响； 张旭东[4]和徐岩等[5]对盾构隧道穿越富水砂层的施工技术进行了探讨； 赖金星等[6-8]以隧道涌水导致衬砌背后空洞事故为依托，采用现场实测和数值模拟的方法分析了空洞位置、大小对盾构隧道的影响及管片裂缝、破损及错台等病害，分析了涌水导致的病害及原因； G. Anagnostou等[9]利用数值模拟方法研究了渗流对土压平衡盾构隧道开挖面稳定性的影响； 刘印等[10]和张冬梅等[11]研究了管片漏水对隧道的长期影响，但没有考虑施工过程中开挖面涌水对隧道的影响。在盾构施工过程中，当土压平衡盾构经过高水压砂层、承压含水层、岩溶地层时，极易引起涌水涌砂事故，通常采取的施工措施是降低盾构掘进速率、关闭螺栓输送机阀门，并对开挖面添加泡沫来进行渣土改良，这样能够迅速止水，以防止引起更加严重的次生灾害，如地表沉降过大、建筑物塌陷、管片挤压破坏等。

盾构掘进过程中高水压引起的灾害一直是隧道工程的研究热点，由于问题的复杂性以及没有合适的分析方法和手段，所以没有形成一套理论来指导工程实践，工人只能靠经验来施工，因而具有一定的盲目性。本文采用现场实测与数值模拟相结合方法，通过对盾构隧道掘进过程进行精细化数值建模，考虑水土流固耦合作用，分析开挖面涌水量对地表沉降以及对管片和螺栓内力的影响，通过建立涌水量与管片螺栓内力的定量关系来厘清涌水灾害对隧道结构内力的影响。

1 工程概况

武汉地铁7号线小东门至武昌火车站盾构区间途经繁华地段及重要交通枢纽，如小东门站立交桥、武九铁路、京广铁路、黄鹤楼公园、大东门立交桥、纽宾凯新宜国际酒店等，区间平面图见图1，盾构隧道施工过程中需严格监测和控制地表沉降。此外，本区间位于长江河谷道，地下水与长江水相通，潜水水位位于地表以下0.5～4.2 m，隧道掘进段经过岩溶地质、承压水、暗河等恶劣地质条件。

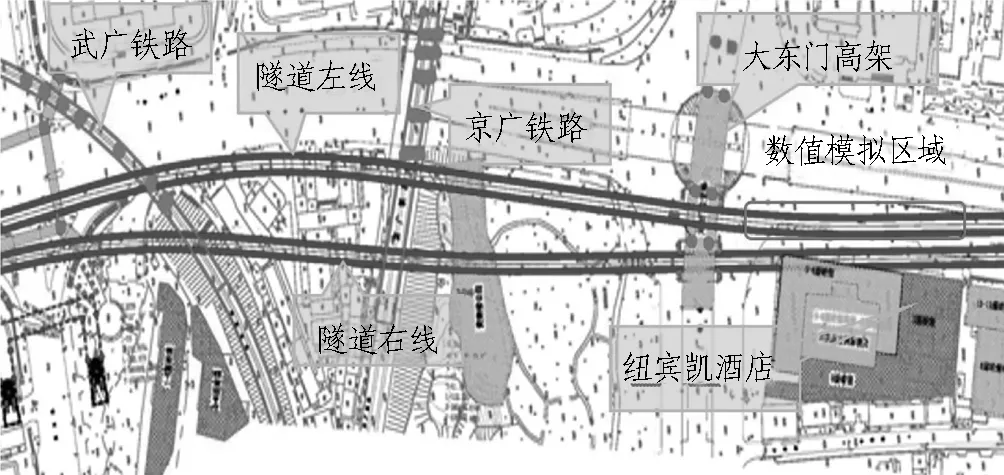
图1 地铁施工区间平面图

本研究的开挖面分3种工况，分别为不排水(工况1)、排水量较小(工况2)、局部排水量较大(工况3)。正常掘进段的分层土体剖面见图2，其开挖面排水控制良好，土层包含7层，从上至下分别由杂填土、粉质黏土、含黏性土细砂、硬泥岩组成，地下水位假定为-1.5 m，杂填土以下土体均为饱和土体，以此作为工况1和工况2的研究背景。隧道经过硬质泥岩区域时泥岩局部夹杂粉细砂层，此泥岩段出现严重涌水险情(见图3)，作为开挖面大量涌水对管片螺栓内力影响即工况3的研究背景。工况3的地质剖面见图4，土层分为5层，从上至下为杂填土、粉质黏土、强风化砂岩、中风化泥岩(夹粉细砂层)、石英夹泥岩。首先，选取图2中的地质条件作为正常施工模拟区段，通过对比现场实测数据与数值模拟结果，来验证数值模拟的可靠性； 然后，以图4中泥岩夹粉细砂地质条件为研究背景，通过分析管片螺栓内力及变形来研究开挖面排水对结构内力的影响。

图2 正常掘进段土体剖面图(单位： m)

图3 施工现场大量涌水涌砂

2 水文地质参数

场地上层滞水初见水位在地面以下1.20～2.50 m，孔隙承压水赋存于长江古河道的〈11-1〉含黏性土粉细砂、〈11-2〉含黏性土细中砂及〈12〉中细砂混砾卵石中，接受周围区域水体渗透补给。岩溶裂隙水主要赋存于灰岩、泥质灰岩的岩溶裂隙中，一般在岩溶发育地段集中分布，局部具有弱承压性。现假定杂填土以下均为饱和土，表示有充足的水源补给且水头恒定，工况3出现大量涌水涌砂段，其中风化泥岩〈19c-2〉夹杂有粉细砂层〈11-1〉，其渗透系数见表1。

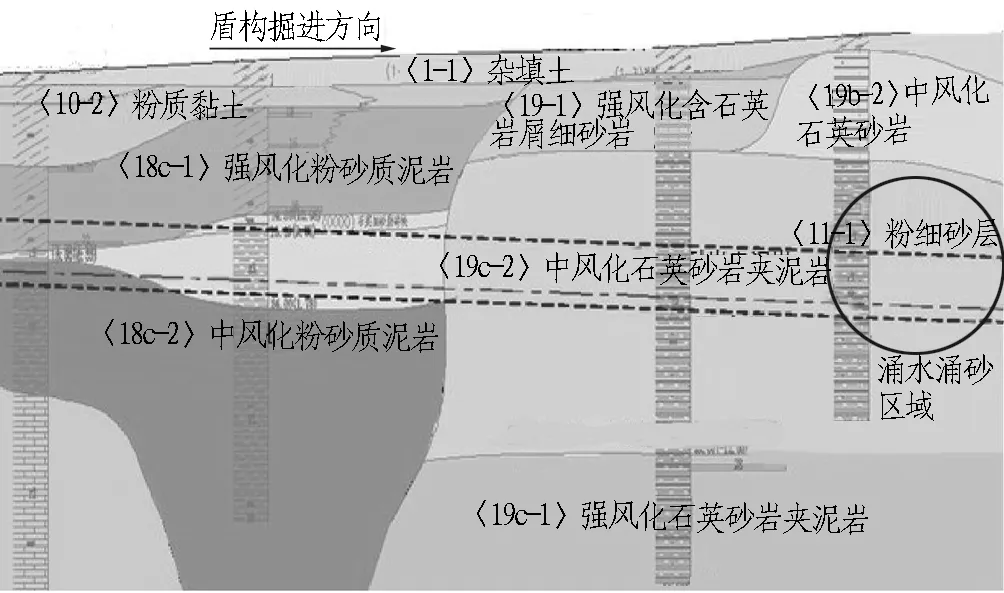
图4 涌水涌砂区间剖面图

工程地质勘测报告提供的土体力学性能数有压缩模量、黏聚力、内摩擦角、孔隙比、密度及渗透系数。通过整理地勘报告，得到数值模拟区间的土体基本力学参数，如表1所示。

3 盾构隧道施工的数值模拟

3.1模型参数

通过理论公式转化可得到土体的弹性模量E0来进行数值模拟，即E0=ESβ，其中ES为压缩模量，β=(1-μ-2μ2)/(1-μ)，μ为泊松比。土体采用理想弹塑性摩尔-库仑(M-C)屈服准则，在开挖过程中，隧道周围土体经历卸载过程，理想弹塑性摩尔-库仑模型假定土体卸载模量等于加载模量，但其数值结果会造成隧道底部隆起量较大。由土体加卸载曲线可知，土体在复杂应力状态下的卸载模量大小取决于土体性质及应力状态。针对土体加卸载模量存在差别的这种性质，王海波等[12]提出地下工程开挖模型中卸载模量可取加载模量的2～4倍，一些学者利用Plaxis软件提供的土体硬化模型来模拟隧道开挖，将卸载模量与加载模量之比取为2～3[13-15]。ABAQUS软件不提供土体硬化模型(H-S)，现将隧道周围土层即粉细砂层〈11-1〉及细中砂层〈11-2a〉的弹性模量增大1倍，见表1。

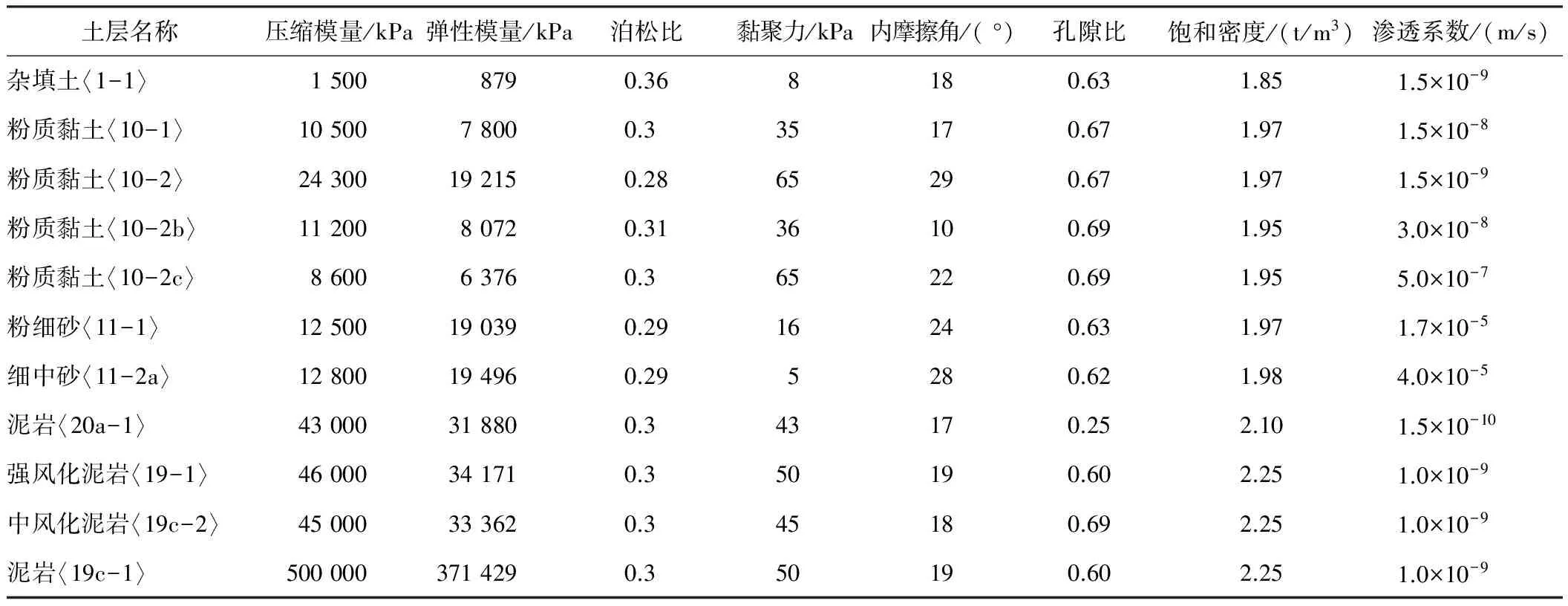
表1 土体基本力学参数

根据现场施工资料建立数值模型，模型主要由土体、盾构、注浆层、管片、螺栓5部分组成。将盾构机体、注浆层及管片假定为线弹性材料，利用等代层模拟盾尾浆体的硬化过程[16]，并考虑管片接头及螺栓，弯曲螺栓直径为30 mm，以上部件的具体尺寸及基本力学参数见表2。注浆层分为软注浆层和硬注浆层，根据现场施工参数，平均每一环注浆量为7 m3，考虑到盾尾浆体渗透及失水引起的体积损失，在富水砂层中的注浆量一般为开挖空隙的130%～180%[17]。结合现场情况，施工模型的注浆层厚度假设为0.14 m，根据每一环土体间隙体积可算出其注浆比为167%，对管片外环及土体内壁施加注浆压力来模拟盾尾注浆压力。

表2 数值模型的基本参数

正常掘进段的数值模型高为50 m、宽为100 m、长为96 m，如图5所示。为减小盾构与土体的摩擦及控制盾构转弯，并考虑实际施工过程中盾构存在土体超挖的情况，由于ABAQUS不方便模拟盾构机体的圆锥度，也不便采用三维应力释放法，本模型在盾构外壁引入一层薄的超挖层来模拟土体超挖[18]，根据盾构的几何尺寸，刀盘外径为6.48 m，盾尾外径为6.4 m，因此现将超挖厚度定为0.04 m，在掘进过程中，既能简化盾构圆锥度的影响，又能使围岩应力得到一定程度的释放，使数值模拟更加贴近实际。

图5 三维模型

根据管片实际尺寸，每一环管片由3块标准块A1、A2、A3，2块相邻块B1、B2以及封顶块K组成，如图6所示。假定混凝土为线弹性材料，为了简化分析，并未考虑管片接头的止水带，考虑环向接头的凹凸槽，管片接头正向采用硬接触，切向采用库仑摩擦接触，切向摩擦因数为0.62，螺栓采用梁单元，将弯曲螺栓梁单元嵌入到管片内[19]。为了防止部件相互“刺入”，管片与注浆层也采用硬接触及库仑摩擦接触，切向摩擦因数为0.7。浆体外侧与土体采用Tie连接。

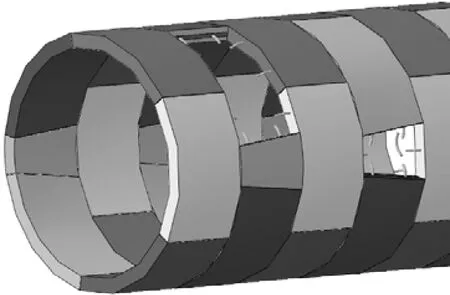
图6 精细化管片及螺栓

3.2模型边界及模拟过程

本文采用的是流固耦合数值模拟方法，因此模型的边界条件分为渗流边界和力学边界。渗流边界是利用ABAQUS的Soils瞬态分析步模拟水土体的流固耦合作用。由于现场盾构施工速度较快，管片止水效果良好且水体补给较快，因此将杂填土与粉质黏土交界处孔压边界设置为0，即为常水头，除开挖面外，其他部位均为不排水边界。力学边界的模型底部为固定边界，约束模型侧面的法向位移，顶部为自由面。

开挖过程中设置开挖面支护力以及盾尾同步注浆压力。根据现场反馈的数据，将开挖面支护力取为400 kPa，开挖面支护力随深度线性增加，梯度增量为20 kPa/m，其作用力稍大于侧向静止水土合力。根据现场施工监测数据，盾尾注浆压力为0.15～0.3 MPa，即最大注浆压力为0.3 MPa，但监测数据只限于浆体泵送管处的注浆压力，由于浆体在盾尾空隙的扩散填充，注浆压力会有一定的耗散。根据实际经验，将注浆压力取为0.2 MPa，并均匀地作用于土体内壁及管片外壁。

本模型具体开挖步骤如下： 1)盾构机体全部进入土体，施加开挖面支护力，盾构外环与土体Tie绑定连接； 2)激活前方盾构环，同时添加衬砌管片和等代注浆层，对土体内壁和衬砌外环施加注浆压力，并对开挖面施加支护力； 3)当管片注浆层已支护4环，注浆压力持续长度为6 m，此时为软化浆体，浆体模量为7 MPa； 4)4环以后，改变浆体模量使其增至50 MPa，以模拟浆体硬化。依此步骤模拟隧道开挖过程。

4 实测与数值模拟结果分析

4.1开挖面涌水对地表沉降的影响分析

地表横向、纵向观测轴线沉降曲线分别见图7和图8，t为数值模型开挖分析步时间，符合隧道开挖的地表沉降规律[20]，地表最大沉降为4.5 mm，如图8所示。由于开挖面支护力稍大于静止水土侧压力，盾构前上方地表有轻微上抬。

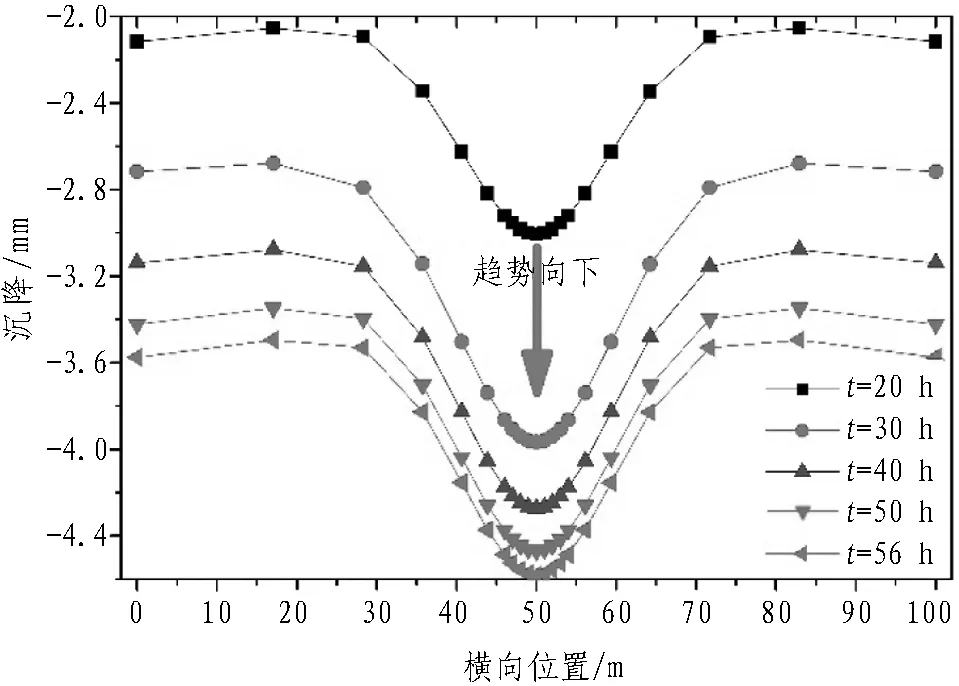
图7 地表横向观测轴线沉降曲线(工况1)

实测点地表沉降值与数值结果进行对比，比较了隧道周围土体取值2倍和3倍的土体模量的数值计算结果，见图9。由图9可知： 3倍土体模量稍微大于2倍土体模量的计算结果，隧道周围土体模量为2倍的数值结果更加贴近实测值，因此本模型下均按2倍土体模量计算。监测点下方土体在盾构经过时开挖面排水控制较好，将开挖面水力边界设置为不排水边界。数值模型与现场实测结果具有很好的一致性，证明数值模型的可靠性。当盾构刀盘经过监测点之前，刀盘前上方的地表土体出现轻微上抬； 当盾构刀盘经过监测点正下方时，由于盾构的超挖，地表开始急剧沉降； 当盾尾经过监测点下方后，土体缺少支护，而后由于盾尾注浆及管片支护的作用，使得土体下沉得到抑制，但由于盾构对土体扰动较大，地表继续下沉，当浆体硬化一段时间后，土体由管片及硬化浆体共同支护，地表沉降最终趋于稳定。

图8 地表纵向观测轴线沉降曲线(工况1)

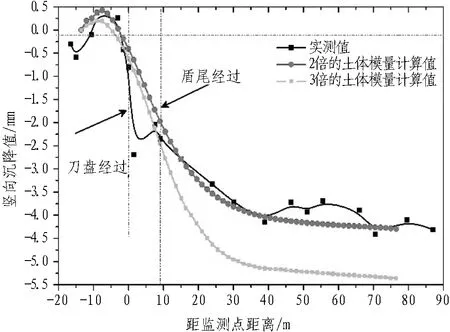
图9 地表监测点沉降值(工况1)

工况2(即开挖面涌水量较小)时地表监测点的沉降值与时间的关系见图10。开挖面渗流速度对应的涌水量见表3。图10中，v=0 m/s表示不排水情况下的监测点沉降时间曲线，而v=3×10-7、1×10-6、3×10-6、5×10-6m/s分别表示开挖面涌水量为0.04、0.12、0.36、0.59 m3时的开挖面渗流速度。由此可以推断，现场大致排水范围在0.04～0.59 m3。

地表最大沉降量与开挖面涌水量的关系见图11。由图可知： 增大开挖面支护力能减小地表沉降，但支护力不宜过大，否则较大的支护力会使隧道正前方地表出现轻微隆起，因此为了减少土体扰动，开挖面支护力宜控制在一定范围内。然而，当盾构隧道开挖面处于排水状态时，增大开挖面支护力并不能从根本上解决地表沉降量较大的问题，在不同的开挖面支护力下，开挖面排水量与地表最大沉降量呈线性关系。因此，盾构在高水压富水砂层掘进过程中，通过控制开挖面排水量是控制地表沉降的根本办法。

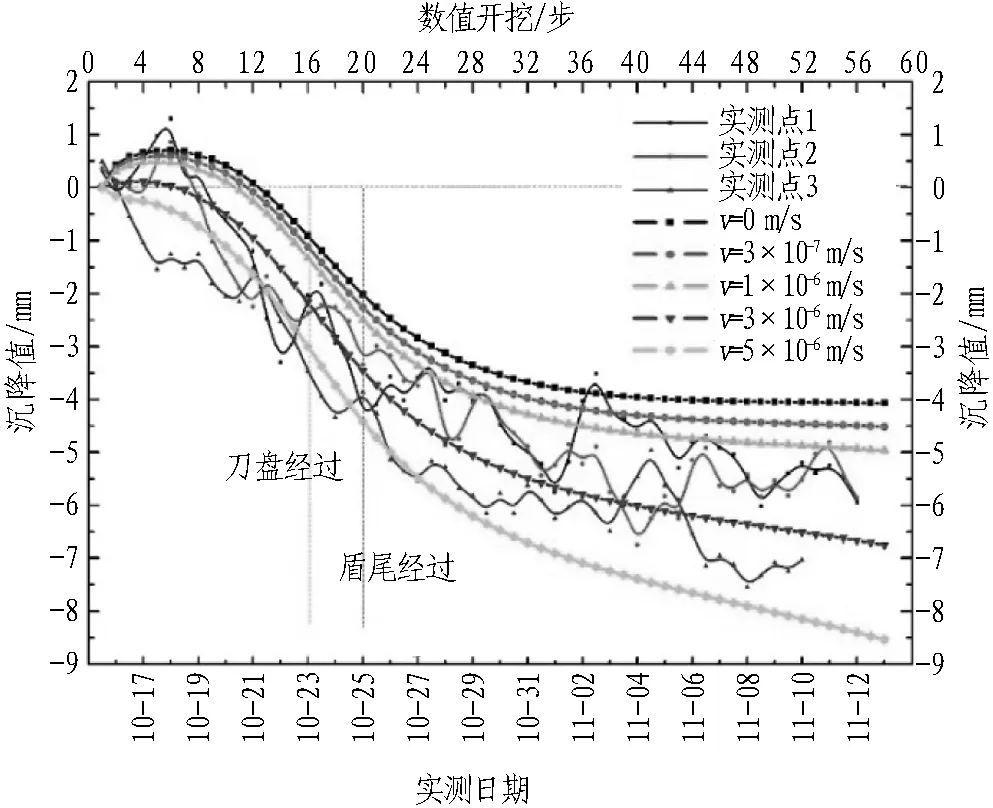
图10 不同涌水量下地表沉降值(工况2)(2016年)Fig. 10 Ground surface settlements under different water inrush volumes in 2016 (case 2)

表3开挖面渗流速度对应的涌水量
Table 3 Relationship between water seepage speeds and water inrush volumes

渗流速度/(m/s)涌水量/m33×10-70．041×10-60．123×10-60．365×10-60．592×10-52．375×10-55．94渗流速度/(m/s)涌水量/m31×10-411．871．5×10-417．812×10-423．752．5×10-429．683．3×10-438．594×10-447．49

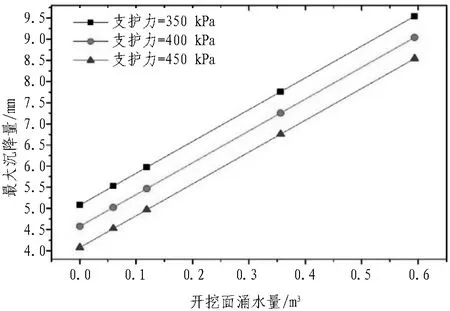
图11 地表最大沉降量与开挖面涌水量的关系Fig. 11 Relationships between maximum ground surface settlements and water inrush volumes at tunneling face

在现场盾构施工过程中，由于地质的复杂性及施工的盲目性，盾构在高水压粉细砂层中掘进时，如果没有及时控制好开挖面排水，会造成涌水涌砂的险情。当开挖面大量涌水涌砂时，隧道上方土体严重下沉，使得管片发生挤压变形，进而破坏管片及螺栓的结构性能。

4.2局部区间开挖面涌水对隧道结构内力的影响

盾构的选型对于施工安全至关重要，选择土压平衡盾构还是泥水盾构需综合考虑土质、渗透系数、工期等自然及人为因素。若初步确定以土压平衡盾构作为施工机具，盾构在掘进过程中，当开挖面前方局部遇到高水压粉细砂层、岩溶、高承压水等恶劣地质条件时，由于土压平衡盾构的螺旋输送机将土舱土体直接输出，如不采取土体改良措施，很容易使开挖面出现涌水涌砂险情，据此为背景研究局部区域开挖面涌水对隧道结构内力的影响。

施工现场局部开挖面涌水涌砂的数值模型见图12，排水区间的孔隙水压力较小。结合现场施工情况及相应地段的工程地质参数(见图3及表1)，盾构最初在土质条件较好的泥岩地层中掘进时，开挖面并无涌水情况发生； 当经过高水压粉细砂层、暗河、岩溶等局部含水量丰富的地层时，土压盾构施工极易造成开挖面出现严重的涌水涌砂险情，进而引发后方管片发生错台及开裂等灾害，风险较大。在图12所示的数值模型中假定泥岩中夹杂着粉细砂层，且经过此砂层时对开挖面设置不同的排水边界，通过开挖面涌水量来反映开挖面涌水情况，精细化模拟管片及螺栓，以工况3为研究背景，分析开挖面涌水对管片及螺栓内力的影响。

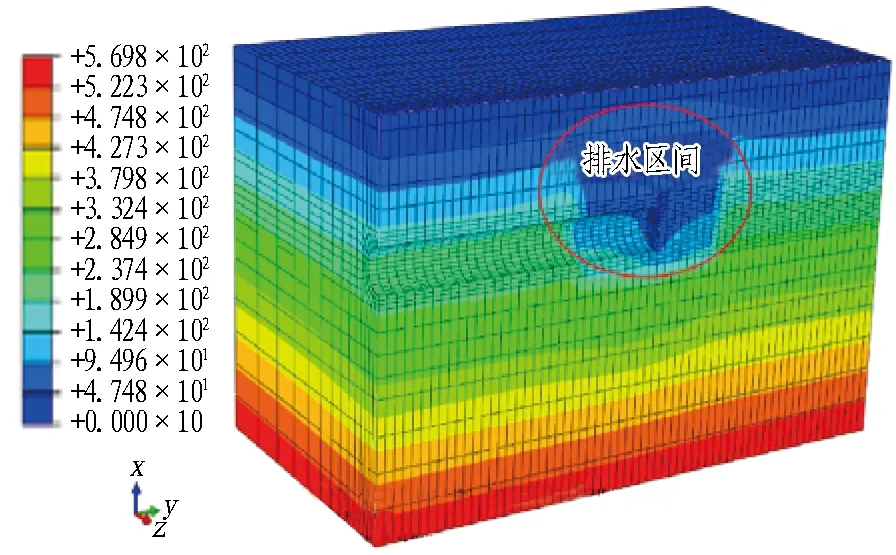
图12 开挖面涌水区域孔隙水压力云图(单位： kPa)Fig. 12 Nephogram of pore water pressure at water inrush area (unit: kPa)

以下进行参数分析，将开挖面渗流速度设置为4×10-4、3.3×10-4、2.5×10-4、2×10-4、1.5×10-4、1×10-4、5×10-5、2×10-5m/s等8种情况来监测管片位移及内力变化，对应的涌水量大小见表3。

开挖面涌水量为47 m3时，开挖面涌水对隧道整体变形影响的位移见图13。由图13可知： 由于开挖面发生大量水体流失，使得隧道上方土体下沉量较大，直接挤压到盾构后方的管片。

图13 隧道整体变形云图(工况3)(单位： m)

盾尾管片的整体变形见图14，管片挤压变形见图15。由图14可知管片最大变形一般发生在盾尾4—5环之后。由图14和图15可知： 管片最大挤压变形位于拱顶，最大下沉量为22.9 mm，管片环向接头张开量较大，因此在拱顶环向接头处容易出现管片及螺栓的应力集中现象。

图14 盾尾管片的整体变形云图(工况3)(单位： m)

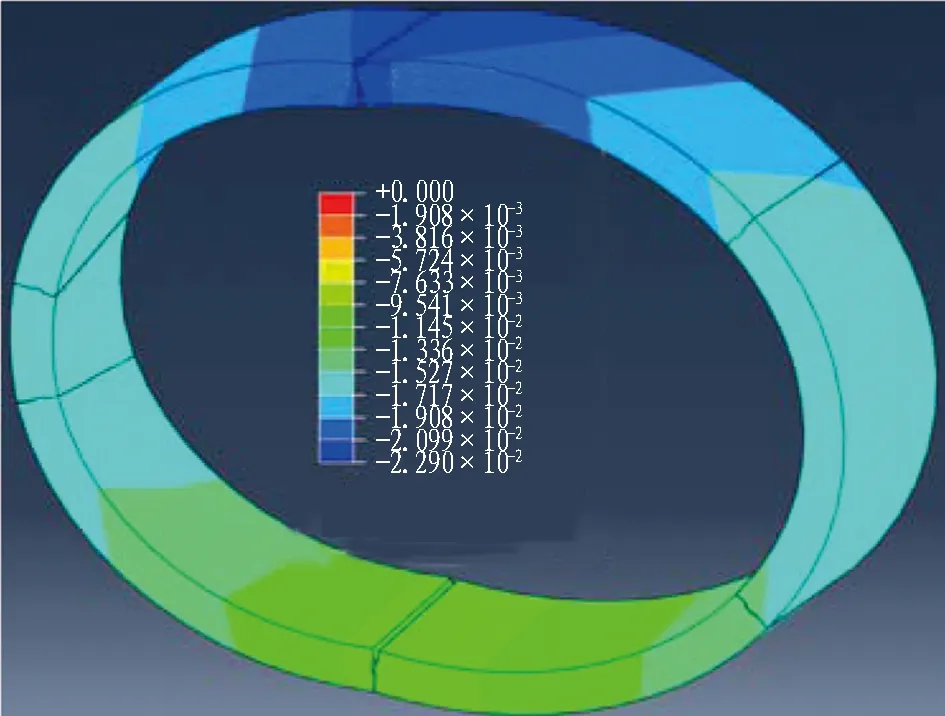
图15 管片挤压变形云图(工况3)(单位： m)

管片最大拉应力、最大压应力分别见图16和图17。可见管片环缝变形严重并使管片接头处出现应力集中，当管片的抗拉强度超过极限抗拉强度时，就会引起管片屈服开裂。螺栓的拉力、剪力及弯矩分别见图18—20，其最大值均位于隧道拱顶。由此可知，盾构在高水压粉细砂层掘进过程中，当隧道开挖面出现大量涌水涌砂险情时，隧道衬砌上方的土体下沉量较大，会直接挤压到拱顶管片，使拱顶纵缝及环缝产生较大的张开量及错台量，进一步使得环缝处的纵向连接螺栓及管片接头出现较大的应力集中。因此，在施工过程中，当开挖面出现大量涌水涌砂险情时，盾尾4—5环后的拱顶管片环向接头是最薄弱和危险的部位，应重点加强防范。

图16 管片最大拉应力云图(工况3)(单位： kPa)Fig. 16 Nephogram of maximal tension stress of segment (case 3) (unit: kPa)

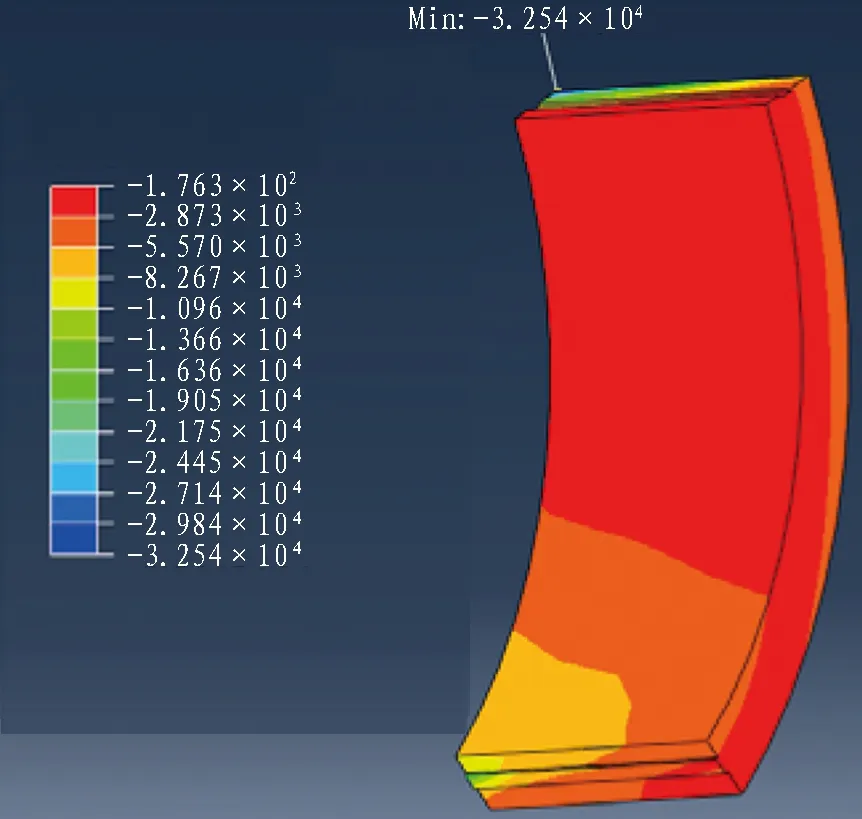
图17 管片最大压应力云图(工况3)(单位： kPa)Fig. 17 Nephogram of Maximal compression stress of segment (case 3) (unit: kPa)

图18 螺栓最大拉力云图(工况3)(单位： kN)Fig. 18 Nephogram of maximal tension stress of anchor bolt (case 3) (unit: kN)

图19 螺栓最大剪力云图(工况3)(单位： kN)Fig. 19 Nephogram of maximal compression stress of anchor bolt (case 3) (unit: kN)

图20 螺栓最大弯矩云图(工况3)(单位： kN·m)Fig. 20 Nephogram of maximal bending moment of anchor bolt (case 3) (unit: kN·m)

开挖面不同排水量对每一环的管片最大变形、管片最大拉应力、管片最大压应力、螺栓最大拉力、螺栓最大剪力、螺栓最大弯矩的影响分别见图21—26。图中Q=47、39、30、24、18、12、6、2 m3分别指盾构推进一环时，开挖面渗流速度对应的排水量为47、39、30、24、18、12、6、2 m3，排水长度持续4环即6 m，以不排水条件为参照。由图21—26可知： 在排水段，随着开挖面逐步涌水，管片变形及螺栓内力均出现较大的增加，当开挖面停止排水时，内力及变形趋于稳定。此外，随着开挖面涌水量的增加，管片变形及螺栓内力都有明显的提升，当开挖面停止涌水涌砂时，管片内力也开始逐步趋于平缓。由此说明开挖面排水对于管片及螺栓的内力影响较大。

在实际工程中，管片的拉应力达到极限抗拉强度时会开裂甚至破坏，螺栓达到屈服强度时会发生屈服断裂，所以应采取紧急抢险措施来控制开挖面的涌水量以降低管片破裂的风险。

图21 管片最大变形值

图22 管片最大拉应力

图23 管片最大压应力

图24 螺栓最大拉力

图25 螺栓最大剪力

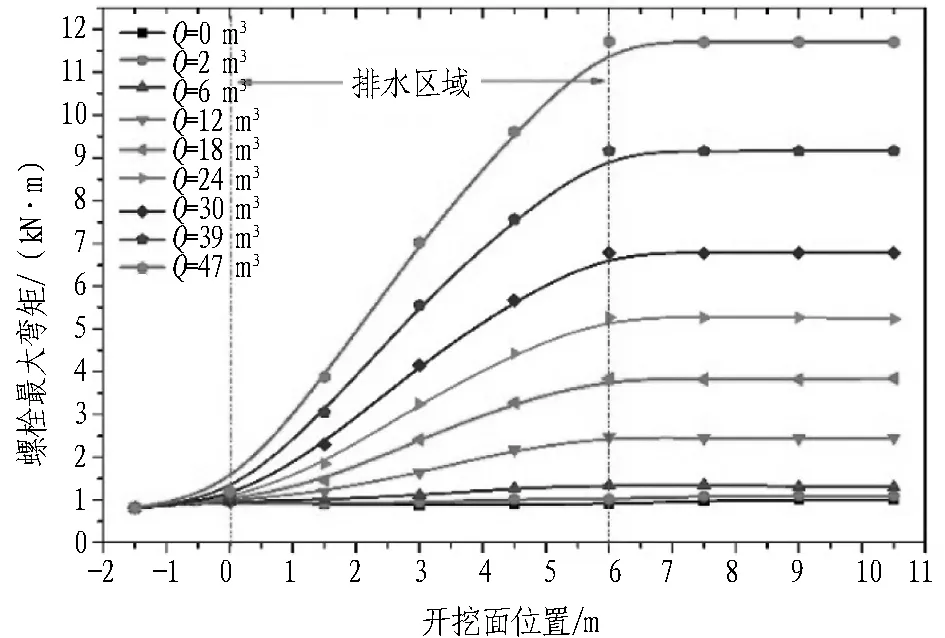
图26 螺栓最大弯矩

通过分析排水区域的不同渗流速度对整个施工过程的影响，整理出隧道整个排水过程中管片最大变形、管片最大拉应力、管片最大压应力、螺栓最大拉力、螺栓最大剪力、螺栓最大弯矩随开挖面涌水量的变化趋势，如图27—32所示。由图27—32可知： 当开挖面涌水量增加时，管片变形内力及螺栓内力都呈现出非线性的增长趋势。对于C50钢筋混凝土管片，其极限抗拉强度约为5 MPa，图28中超出抗拉强度部分的涌水量范围用虚线表示。当管片内力超过其抗拉强度时，管片就会出现裂纹，进而导致管片接头破损，从而影响管片接头的防水性能，继而引起更加严重的管片接头渗漏水灾害。对于高强度螺栓M30，其可承受的最大剪力为381.7 kN，图30—32中虚线表示使螺栓发生屈服的涌水量范围，复杂应力下会导致螺栓发生屈服破坏，威胁工程结构及施工安全。因此，发生开挖面涌水灾害时，为了降低管片压裂风险，必须采取相应的补救措施将开挖面涌水量控制在一个很低的水平，将灾害风险降至最低。

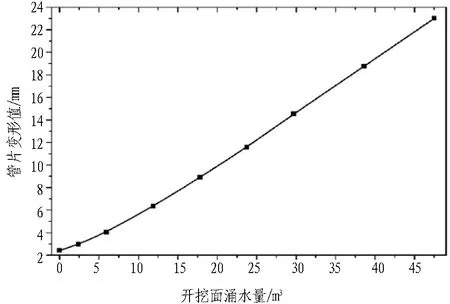
图27 涌水量对应的管片最大变形

图28 涌水量对应的管片最大拉应力

图29 涌水量对应的管片最大压应力Fig. 29 Maximal segment compression stress vs. water inrush volume

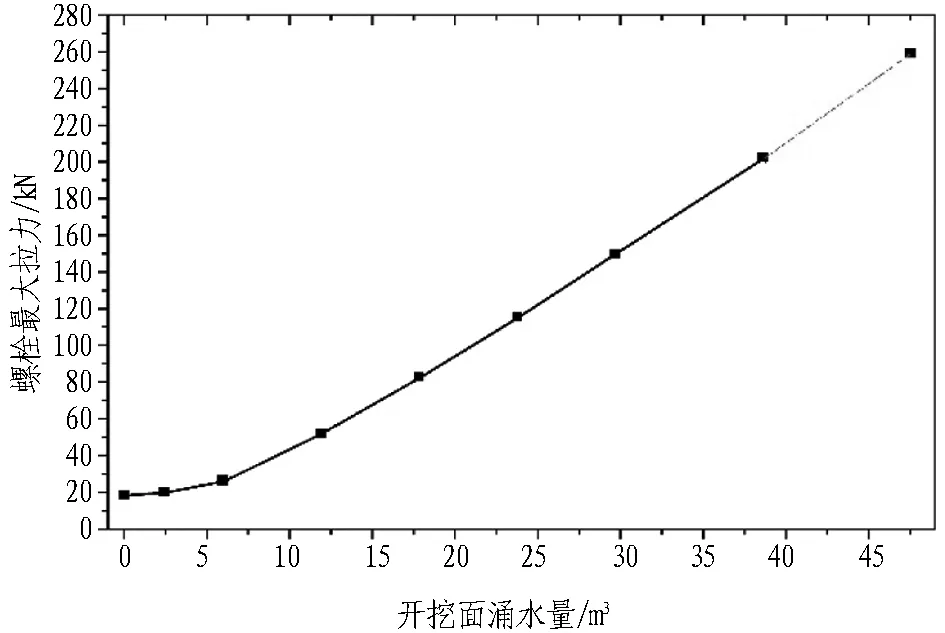
图30 涌水量对应的螺栓最大拉力Fig. 30 Maximal anchor bolt tension stress vs. water inrush volume

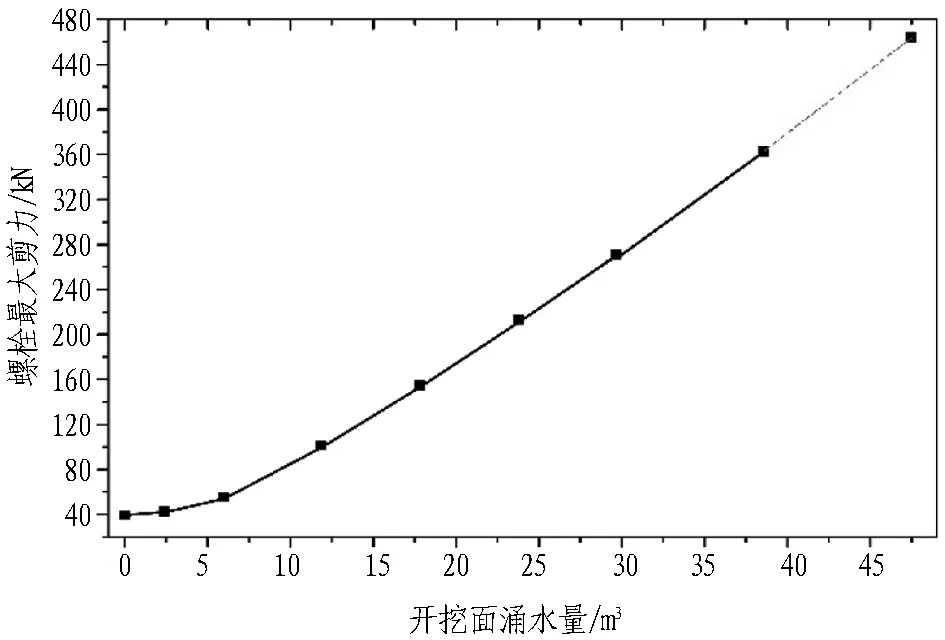
图31 涌水量对应的螺栓最大剪力

图32 涌水量对应的螺栓最大弯矩Fig. 32 Maximal anchor bolt bending moment vs. water inrush volume

5 结论与讨论

以武汉地铁7号线小东门至武昌火车站区间为研究背景，结合精细化数值模型方法，研究开挖面涌水对地表沉降及管片、螺栓内力变形的影响，得到以下主要结论。

1)隧道开挖面涌水量对地表沉降有非常重要的影响。当土压盾构掘进经过高水压砂层时，可通过降低掘进速度及土舱土体的渗透系数等减小开挖面涌水量的措施来减小地下水流失，或者适当增大开挖面支护力，进而达到降低地表沉降的目的。

2)由数值结果可知开挖面涌水造成隧道上方的土体下沉量较大，使得拱顶管片挤压变形，拱顶环缝张开量较大，进而使连接螺栓及管片接头处产生应力集中。因此，在施工过程中当隧道开挖面出现严重的涌水涌砂险情时，拱顶管片的环向接头是最薄弱的部位，应重点防范。

3)隧道开挖面涌水量较大时，会使盾构后方土体塌陷且作用于管片上，管片及螺栓的内力与变形均呈现非线性增长的趋势，增大了管片错台与挤压开裂的风险，增加了管片接头的涌水涌砂风险灾害。因此，为防止隧道内部结构破坏，当土压盾构在高水压粉细砂层中掘进时应采取相应的施工措施来降低开挖面的涌水量，以防灾害进一步恶化。

同时，本研究也存在一些不足及需要深化的地方：

1)通过厘清开挖面涌水量对土压平衡盾构隧道破坏的灾变机制，制定出土压平衡盾构的开挖面涌水量控制标准，以便指导工程实践。

2)为了更加准确地模拟管片及螺栓破坏的灾害演变过程，可通过建立精细化数值模型来厘清盾构隧道施工过程中由于高水压引起的灾害机制，如考虑管片的混凝土损伤本构模型及螺栓塑性模型，将管片接头破坏引起的渗漏水(渗透系数)与管片损伤程度(损伤因子)结合起来，实现真正意义上的流固耦合。

[1] 朱自鹏. 砂卵石地层高水压条件下土压平衡盾构防喷涌研究[D]. 北京： 北京交通大学， 2016.

ZHU Zipeng. Study of anti-blowout induced by EPB shield tunneling under high water pressure in sandy cobble stratum[D]. Beijing: Beijing Jiaotong University, 2016.

[2] 张远荣. 盾构过富水砂层对环境影响的分析研究[D]. 北京： 中国铁道科学研究院， 2010.

ZHANG Yuanrong. Environmental influence analysis of shield tunneling in watere-rich sandy stratum[D]. Beijing: China Academy of Railway Sciences, 2010.

[3] 朱玉龙, 赵青, 晏启祥.土压平衡盾构隧道下穿城市景观河道受力特性模拟研究[J]. 路基工程, 2016(6): 68.

ZHU Yulong，ZHAO Qing，YAN Qixiang. Simulation research on stress characteristics of the EPB shield tunnel across the city landscape riverway [J]. Subgrade Engineering， 2016(6): 68.

[4] 张旭东. 土压平衡盾构穿越富水砂层施工技术探讨[J]. 岩土工程学报， 2009， 31(9): 1445.

ZHANG Xudong. Construction technology of earth pressure balance shield in watery sandy stratum[J]. Chinese Journal of Geotechnical Engineering， 2009， 31(9): 1445.

[5] 徐岩， 赵文， 黄龙光， 等.富水砂层土压平衡盾构关键施工技术[J]. 施工技术， 2011， 40(7): 71.

XU Yan，ZHAO Wen，HUANG Longguang，et al. Key construction technology of earth pressure balance shield in watery sandy stratum[J]. Construction Technology， 2011，40(7): 71.

[6] 赖金星， 刘炽， 胡昭， 等. 盾构隧道衬砌背后空洞对结构影响规律数值分析[J]. 现代隧道技术， 2017, 54(3): 126.

LAI Jinxing， LIU Chi， HU Zhao， et al. Numerical analysis of the influence of a cavity behind the shield lining on the tunnel structure[J]. Modern Tunnelling Technology， 2017，54(3): 126.

[7] 赖金星, 邱军领, 潘云鹏， 等. 盾构隧道管片裂缝病害的综合监测与分析[J].现代隧道技术， 2015， 52(2): 186.

LAI Jinxing, QIU Junling, PAN Yunpeng，et al. Comprehensive monitoring and analysis of segment cracking in shield tunnels[J]. Modern Tunnelling Technology， 2015， 52(2): 186.

[8] 赖金星, 汪珂, 刘炽， 等. 黄土地层盾构隧道衬背空洞注浆过程变形规律[J]. 解放军理工大学学报(自然科学版)， 2015， 16(3): 231.

LAI Jinxing，WANG Ke，LIU Chi，et al. Numerical investigation and monitoring of deformation law of loess shield tunnel during backing void grouting process[J].Journal of PLA University of Science and Technology(Natural Science Edition)， 2015， 16(3): 231.

[9] ANAGNOSTOU G， KOVARI K. Face stability conditions with Earth-Pressure-Balanced shields[J]. Tunnelling and Underground Space Technology, 1996， 11(2)： 165.

[10] 刘印, 张冬梅, 黄宏伟. 盾构隧道局部长期渗水对隧道变形及地表沉降的影响分析[J]. 岩土力学, 2013， 34(1): 290.

LIU Yin， ZHANG Dongmei， HUANG Hongwei. Influence of long-term partial drainage of shield tunnel on tunnel deformation and surface settlement[J]. Rock and Soil Mechanics， 2013， 34(1): 290.

[11] 张冬梅, 刘印, 黄宏伟. 软土盾构隧道渗流引起的地层和隧道沉降[J]. 同济大学学报(自然科学版), 2013，41(8): 1185.

ZHANG Dongmei, LIU Yin，HUANG Hongwei. Leakage-induced settlement of ground and shield tunnel in soft clay[J]. Journal of Tongji University(Natural Science), 2013，41(8): 1185.

[12] 王海波, 宋二祥, 徐明. 地下工程开挖土体硬化模型[J]. 清华大学学报(自然科学版), 2010， 50(3): 351.

WANG Haibo, SONG Erxiang, XU Ming. Hardening-soil-model for underground construction[J].Journal of Tsinghua University (Science & Technology), 2010， 50(3): 351.

[13] BILOTTA E, PAOLILLO A, RUSSO G， et al. Displacements induced by tunnelling under a historical building[J]. Tunnelling and Underground Space Technology， 2017, 61： 221.

[14] ZHAO Chenyang, LAVASAN A A, BARCIAGA T, et al. Prediction of tunnel lining forces and deformations using analytical and numerical solutions[J]. Tunnelling and Underground Space Technology, 2017, 64： 164.

[15] 姜晓婷, 路平, 郑刚, 等. 天津软土地区盾构掘进对上方建筑物影响分析[J]. 岩土力学, 2014, 35(增刊2)： 535.

JIANG Xiaoting, LU Ping, ZHENG Gang， et al. Influences on surface structure induced by shield tunneling in Tianjin soft ground area[J]. Rock and Soil Mechanics， 2014, 35(S2)： 535.

[16] 张云, 殷宗泽, 徐永福. 盾构法隧道引起的地表变形分析[J]. 岩石力学与工程学报, 2002, 21(3): 388.

ZHANG Yun，YIN Zongze，XU Yongfu. Analysis of three-dimensional ground surface deformations due to shield tunnel[J]. Chinese Journal of Rock Mechanics and Engineering， 2002, 21(3): 388.

[17] 杨书江， 孙谋， 洪开荣. 富水砂卵石地层盾构施工技术[M]. 北京： 人民交通出版社， 2011.

YANG Shujiang, SUN Mou, HONG Kairong. Shield tunneling technology in water-rich sandy-cobble stratum[M]. Beijing: China Communications Press, 2011.

[18] KATEBI H, REZAEI A H, HAJIALILUE-BONAB M, et al. Assessment the influence of ground stratification, tunnel and surface buildings specifications on shield tunnel lining loads (by FEM)[J]. Tunnelling and Underground Space Technology, 2015, 49: 67.

[19] 艾辉军, 彭立敏, 施成华. 基于三维非连续接触模型的管片接头静动力特性分析[J]. 岩土工程学报, 2013， 35(11): 2023.

AI Huijun, PENG Limin, SHI Chenghua. Static and dynamic characteristic analysis of segment joints based on three-dimensional discontinuous contact model[J]. Chinese Journal of Geotechnical Engineering, 2013，35(11): 2023.

[20] 韩煊, 王法, 雷崇红, 等. 盾构隧道施工引起的土层分层沉降规律实测研究[J]. 隧道建设, 2017， 37(4): 401.

HAN Xuan，WANG Fa，LEI Chonghong,et al. Study of rules of ground layered settlement induced by shield tunneling[J]. Tunnel Construction， 2017， 37(4): 401.

AnalysisofInfluenceofWaterInrushatShieldTunnelingFaceonGroundSurfaceSettlementandInternalStressofSegment

YE Zhi, LIU Huabei, LIU Wen*

(SchoolofCivilEngineeringandMechanics,HuazhongUniversityofScienceandTechnology,Wuhan430074,Hubei,China)

The water inrush and mud gushing induced large ground surface settlement and segment deformation would occur during earth pressure balance (EPB) shield tunneling in sandy stratum with high water pressure. A refined numerical model for EPB shield tunneling in Xiaodongmen Station-Wuchang Railway Station section on Wuhan Metro Line No. 7, considering fluid-solid coupling of water and soil, is established so as to study the influences of water inrush at shield tunneling face on ground surface settlement and internal stresses of segment and anchor bolt. The study results show that: 1) The water inrush volume at tunneling face and ground surface settlement show linear relationship; and that and internal stress of segment anchor bolt show nonlinear relationship. 2) Large water inrush volume would lead to squeezing deformation of tunnel crown top, and would further induce damage of segment and yielding of anchor bolt. As a result, attentions should be paid on reducing water inrush volume.

shield tunnel; earth pressure balance (EPB) shield; fluid-solid coupling; numerical simulation; mud gushing and water inrush at tunneling face; ground surface settlement; internal stress of segment; internal stress of anchor bolt

2017-06-20;

2017-08-24

叶治(1990—)，男，湖北崇阳人，华中科技大学岩土工程专业在读博士，研究方向为隧道及地下工程。E-mail： yz1990@hust.edu.cn。*通信作者： 刘文， E-mail: 379047775@qq.com。

10.3973/j.issn.1672-741X.2017.10.011

U 45

A

1672-741X(2017)10-1276-11