基于最优潮流的分布式电源协调控制研究

陈柏森，廖清芬，刘涤尘，王文怡，王志义

(1.武汉大学电气工程学院，湖北 武汉 430072；2.中南电力设计院，湖北 武汉 430071；3.国网黄石供电公司，湖北 黄石 435000)

TK 01

A

2096-2185(2017)05-0030-06

10.16513/j.cnki.10-1427/tk.2017.05.005

基于最优潮流的分布式电源协调控制研究

陈柏森1，廖清芬1，刘涤尘1，王文怡2，王志义3

(1.武汉大学电气工程学院，湖北 武汉 430072；2.中南电力设计院，湖北 武汉 430071；3.国网黄石供电公司，湖北 黄石 435000)

分布式电源作为一种形式广泛、储量丰富、清洁高效的能源，能够很好地解决现有的能源短缺、环境破坏、资源配置等多种问题，且具有良好的经济性，已成为未来电力系统建设和能源系统发展所必须要全面考虑的重要部分；但是在分布式电源并网运行巨大优势的背后，还存在着许多诸如负荷预测、潮流变化、电能质量、功率波动等挑战和问题。提出一种配电网对于接入分布式电源的协调控制技术，将配电网的运行成本作为目标函数，在对负荷预测和分布式电源出力预测的基础上，以及最优潮流及其相关的约束条件下，采用序列二次规划法、内点法及遗传算法3种优化方法进行仿真，得到目标函数的最优值和相应的分布式电源的出力情况；通过对3种不同算法的比较发现，序列二次规划法能够更加有效地完成目标函数的寻优，可快速收敛，其有效支持了配电网对于分布式电源的协调控制技术。

分布式电源；目标函数；最优潮流；协调控制；优化算法

0 引言

分布式电源(distributed generation，DG)能够提高能源的利用效率，节能减排，这些特点促进了其快速发展。DG就近并入配电网，可以减少线路损耗，改善电网的电能质量，缓解供电压力，提高电网的抗灾能力和可靠性[1]。事实上只有在技术层面上满足了一定的条件限制，并且对于接入电网DG的容量进行合理的考虑和规划，选择和电网相符合的类型，选择恰当的接入时间和位置，综合考虑多方因素的影响，才能最大程度地发挥其经济效益。

DG接入到配电网后，配电网将由单一电源模式转变成多种电源模式，配电网的节点电压、网络损耗以及线路潮流等各种参数，都会因DG的接入容量、类型、位置及运行方式发生较大的变化[2]。文献[3]详细探讨了分散电源接入配电网对其电流保护产生的有利和不利影响，并在仿真软件基础上，验证了DG的容量以及并网位置的变化对于各段电流保护的影响，提出了一种能够满足分布式电源并网后配电网保护要求的改进方案；但是其所采用的是传统的三段式电流保护，在如今复杂多变的配电网中很难达到全面的保护要求。文献[4-5]根据DG并网后配电网的拓扑结构特点，对于配电网和分布式电源进行数学建模，通过采取软件仿真以及恰当的潮流计算手段，研究了 DG并网对配电网的电能质量及调压措施的影响过程，并得到了实质性的结果；与此同时，由于DG的接入，整个配电系统的网络结构，包括其运行控制方式都将发生重大的影响变化。显然，如果要实现DG的良性接入，无论是配电网的综合自动化的实现，还是基于用户侧的需求侧管理系统，都在要求将DG与配电网间的协调控制这个重要因素考虑进来，而这无疑会使配电网的控制与管理更加多变且复杂。

本文所要研究的是基于多种类型DG接入配电网，考虑了DG间歇性和出力不确定性，在保证负荷和供电实时平衡的情况下，使系统总运行费用达到最小值，满足经济性要求的同时，电压和潮流不越限；同时采用不同的优化算法，达到快速收敛最优解的目的。

1 最优潮流

1.1最优潮流概述

电力系统最优潮流[6]是电力系统网络运行分析和优化的重要工具，将安全性和经济性、有功、无功功率优化结合在一起，根据给定系统的结构参数和负荷情况，并考虑所有满足要求的约束条件的限制，使目标函数的指标得到理想的最优值；但是由于变量等因素存在一定的误差或变动，理论上会存在多个可行解。最优潮流的任务就是在多个可行解中找到唯一的最优解[7]。通过最优潮流，能够将潮流计算融入电力系统的经济调度当中，通过成本效益方法实现电力系统的可靠性与电能质量与经济指标的对应量化，得到最终的综合经济目标函数，最终实现降低发输电成本以及线路损耗，提高服务质量和系统运行的稳定性和冗余度，达到优化资源配置的效果。

1.2数学模型

在数学上可将最优潮流问题量化为在满足等式和不等式约束(即潮流方程和系统安全限制)的条件下，通过计算方法得到相应控制、状态变量的值，使目标函数(即待求的系统指标)得到最优解，属于非线性规划的问题。目标函数的选择会根据所要达到的目的的不同而进行相应的改变，一般会有系统的运行成本最小、有功损耗最低、切除负荷量最小等，可以统一用下式来表示：

f=minf(u,x)

(1)

最优潮流的等式约束条件一般为节点潮流方程：

式中：PG,k和QG,k为节点k(k=1,2,…，N)处有功、无功的发电功率；PD,k和QD,k为节点k处有功、无功的负荷功率；Pk(u,x)和Qk(u,x)为由u、x计算出的节点k处有功、无功注入功率。

不等式约束(安全限制条件)一般是指电能质量的约束以及电力系统的安全运行，其条件有多个，一般包括：

1) 节点电压的约束。

Ui,min≤Ui≤Ui,max

(4)

2) 电源有功和无功约束。

(5)

3) 输电线路电流约束。

Ili,min≤Ili≤Ili,max

(6)

综上所述，电力系统最优潮流问题的数学模型可表示为

(7)

通过上述内容，建立了最优潮流的基本数学模型，最后在仿真软件中作为计算收敛以及防止结果越限的条件，能够达到很好的效果。

1.3求解方法

为解决复杂的非线性规划潮流问题，良好的数学计算效果是不可或缺的,这其中包含了两方面的内容——足够快的计算速度以及足够优良的收敛性能。历代学者对于求解最优潮流的方法进行了不懈探究，大致归纳起来主要有以下几种：线性和非线性规划法、二次规划法、混合规划法以及日益成熟的人工智能算法。文献[8]为解决满足安全约束的经济调度问题，采用了线性规划法将目标函数(成本费用)和约束条件线性化后，基于单纯形法的内容进行求解；但此算法是从不可行点出发的，在寻优方面有一定的难度。非线性规划法[9-11]主要有简化梯度法、牛顿法、解耦法、内点法等。电网的物理模型结构能通过非线性模型得到很好的描述，被广泛研究和运用于求解最优潮流问题。随着计算机和人工智能技术的发展，越来越多的现代智能算法被开发出来，其运算速度快、收敛性好、占用内存小，最优潮流的求解得到了进一步提升。

2 优化算法

2.1内点法(路径跟踪法)

本文采用的是路径跟踪法，其算法收敛迅速，鲁棒性强，对初值的选择不敏感，其迭代次数与系统规模或控制变量的数目关系不大，适合用于此次目标函数的寻优。内点法的根本原理在于自始至终在可行域内部进行所有的迭代过程。为达到此目的，首先要在可行域内设置合适的初始点；然后要在可行域的边界设置障碍条件，其目的是使当迭代点接近边界时目标函数能迅速增大，从而迭代点都成为可行域的点[12]。而路径跟踪法不再要求必须在可行域内进行迭代求解，而是要求寻优中的拉格朗日乘子及松弛变量满足大于或小于0，这使计算过程得到较大简化[13]。设置松弛变量和拉格朗日乘子的数值使不等式约束变成等式约束。障碍函数具有在可行域内应接近于原函数且边界值很大的特点，因此最后将目标函数与其进行转换，一次便可得到待优化问题B：

(8)

以上函数值会在迭代点接近边界时趋于无穷大，因此也就不可能在边界或者其附近找到满足上述障碍函数的最小值，原来含有不等式限制的优化问题A通过目标函数的障碍变化，变成了只含有等式限制优化的问题B，成为拉格朗日形式的优化问题：

(9)

其潮流计算的流程如图1所示。

图1 内点法最优潮流计算流程图Fig.1 Optimal flow calculation process of interior point method

2.2序列二次规划法

由Powell提出的序列二次规划法是解决非线性规划问题最有效的算法之一[14]，其基本原理为：通过构造一系列简单的近似优化问题对原本的非线性约束优化问题进行逼近简化，根据一连串的线性规划或二次规划来逐次逼近原非线性规划问题，以达到对于迭代过程中迭代点的不断修正。现在，作为求解非线性约束优化问题的一种行之有效的方法，序列二次规划法不仅可求解等式约束优化问题，并且对于不等式约束优化问题的求解也得心应手，此算法具有良好的全局收敛性及超线性收敛的速度。

2.3遗传算法

遗传算法(genetic algorithm, GA)的基本原理是“优胜劣汰，适者生存”，通过对优化问题解的集合中每个体进行编码来模拟生物繁衍进化的体制。为得到最优解或接近最优解的组合，需要通过对已经编码后的优化问题进行组合划分并进行迭代计算，这其中解的个体数是大量的，但是有优劣之分，而评价解优劣的唯一标准就是根据目标函数构造的适应度函数。遗传算法的核心内容是对随机选取的一个子集进行选择、杂交和变异等操作，通过一次又一次的遗传迭代操作，整个群体会以较大的概率保留住问题的最优解而不会被淘汰。

3 协调控制技术

3.1控制变量

由于储能和柴油发电机属于可控的DG，其出力可保持稳定，所以选取二者作为控制变量；而风电机组和光伏发电机组由于本身具有间歇性和出力的波动性，属于不可控DG，出力会随着风速、光照强度等因素实时变动，无法当作控制变量，只能通过出力预测给出基本的数据，参与最优潮流的计算。

3.2目标函数

本文把配电网的整个运行成本费用作为目标函数，该目标函数没有采用一个断层面作为研究对象，而是以整个调度周期的运行成本作为中心着重点进行研究，此举可以得到经济调度的利益最大化，效果显著。为简化计算，接入配电网中的DG均可忽略节能减排的费用部分，同时各DG均认为采用最大功率点跟踪控制模式(maximum power point tracking, MPPT)，实现能源的利用率最大化。目标成本函数F的数学表达式为

(10)

式中：F为目标函数，即配电网的运行成本费用；k′为将整个调度周期进行划分得到的单位阶段数，可近似认为各个DG在各个阶段的出力以及负荷大小，储能单元出力保持不变；ΔT为单个阶段的时间长度；Cf(t) 为t时刻馈线连接的母线节点电价成本，Pf(t)为t时刻馈线出口有功功率；n为可控DG的个数；Ci(t)为第i个可控分布式电源在t时刻的发电成本；PDG-i(t)为第i个可控DG在t时刻的有功出力。

3.3约束条件

本文对于DG出力设置为只发出有功功率，功率因数为1，确保了能源的高效利用。因此在约束条件中，可以不用考虑电源的无功功率的约束。约束条件包括了节点潮流平衡约束、节点电压上下限约束、DG的有功约束，同时还要确保馈线不向上一级反向送电。

(11)

4 算例分析

本文用于此次协调控制的算例[15]是一个含有8个DG、21个节点的配电网系统,如图2所示;各DG的参数配置如表1所示。

3种算法的仿真结果如表2所示，无论是在收敛速度、迭代次数还是寻优效果方面，序列二次规划法相比于内点法和遗传算法都表现出良好的优势。

最后的目标函数最优值为18 299元，相对于原来的成本19 663.06元，经济效益提升了6.94%，优化控制的经济效果比较理想。储能和柴油发电机的出力情况如图3、4所示。最后将基本的节点负荷数据、线路参数和最后得到的优化结果，进行潮流计算来验证是否出现电压越限。检查结果表明，所有节点电压的误差在标准电压范围之内，表明此次优化总体上取得了良好的效果。

图2 算例系统Fig.2 Example system

表1 分布式电源配置参数Table 1 Distributed generation configuration parameters

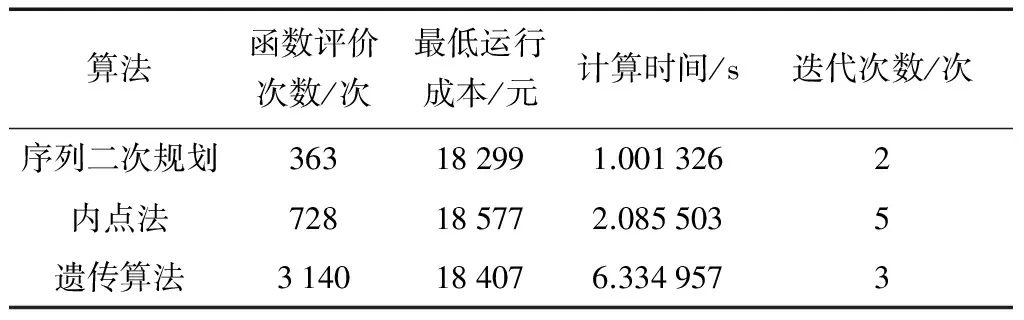
表2 不同算法的比较Table 2 Comparison of different algorithms

图3 储能装置出力Fig.3 Energy storage device output

图4 柴油发电机出力Fig.4 Diesel generator output

5 结论

配电系统接入多个分布式电源以后，带来的潮流变化、电能供需平衡等多个问题亟需得到解决。本文在对不可控DG的出力预测和负荷预测的基础上，基于最优潮流，提出一种配电网对于接入DG的协调控制技术。将配电网的运行成本作为目标函数，在功率和电压的约束条件下，采用了3种不同的优化算法求解出目标函数的最优解，体现了此种协调控制技术良好的经济效益和对于DG出力的合理规划。本文研究的是配电网在正常状态下对DG的协调控制技术，接下来还会对配电网故障状态下的DG孤岛运行的相关内容作进一步研究。与此同时，本文所研究的是基于现有的辐射状网架的配电网，针对以后发展出现的环网甚至更复杂的网络结构，仍要进行深入研究。

[1] 尤毅, 刘东, 钟清, 等. 主动配电网优化调度策略研究[J]. 电力系统自动化, 2014, 38(9): 177-183.

YOU Yi, LIU Dong, ZHONG Qing,et al．Research on optimal schedule strategy for active distribution network[J]． Automation of Electric Power Systems， 2014, 38(9): 177-183.

[2] 王成山, 李鹏. 分布式发电, 微网与智能配电网的发展与挑战[J]. 电力系统自动化, 2010, 18(2): 10-14.

WANG Chengshan, LI Peng. Development and challenges of distributed generation, the micro-grid and smart distribution system[J]． Automation of Electric Power Systems， 2010, 18(2): 10-14.

[3] 李新, 彭怡, 赵晶晶, 等. 分布式电源并网的潮流计算[J]. 电力系统保护与控制, 2009, 17(17): 78-81.

LI Xin, PENG Yi, ZHAO Jingjing, et al． Power flow calculation of distribution network with distributed generation[J]． Power System Protection and Control, 2009, 17(17): 78-81.

[4] 徐群. 分布式电源并网对电能质量的影响分析与评估[D]. 北京： 华北电力大学, 2012.

XU Qun. Analysis and evaluation of the influence of distributed power supply and grid on power quality[D]. Beijing: North China Electric Power University, 2012.

[5] 陈琳, 钟金, 倪以信, 等. 含分布式发电的配电网无功优化[J]. 电力系统自动化, 2006, 30(14): 20-24.

CHEN Lin, ZHONG Jin, NI Yixin, et al． Reactive power optimization of distribution network with distributed generation[J]． Automation of Electric Power Systems， 2006, 30(14): 20-24.

[6] 袁越, 吴涵, 陆丹, 等. 含高渗透率分布式电源的主动配电系统规划综述[J]. 分布式能源, 2016, 1(1): 6-13.

YUAN Yue, WU Han, LU Dan, et al． A review of active distribution system planning with high penetration distributed generation[J]. Distributed Energy, 2016, 1(1): 6-13.

[7] 李冉, 韩旭, 曾鸣, 等. 计及地区特点的分布式电源发展适用性评估[J]. 分布式能源, 2016, 1(2): 14-20.

LI Ran, HAN Xu, ZENG Ming, et al． Applicability evaluation for development of distributed power generation considering regional characteristics[J]. Distributed Energy, 2016, 1(2): 14-20.

[8] WELL D W. Method for economic secure loading of a power system[J]. Proceedings of IEEE, 1968, 115(8): 606-614.

[9] DOMMEL H W, TINNEY W F. Optimal power flow solution[J]. IEEE Transactions on Power Apparatus and Systems, 1968, 87(10): 1866-1876.

[10] BALA J L, THANIKACHALAM A. An improved second order method for optimal load flow[J]. IEEE Transactions on Power Apparatus and Systems, 1978(4): 1239-1244.

[11] 于建成, 迟福建, 徐科, 等. 分布式电源接入对电网的影响分

析[J]. 电力系统及其自动化学报, 2012, 24(1): 138-141.

YU Jiancheng, CHI Fujian, XU Ke, et al． Analysis of the impact of distributed generation on power grid[J]. Proceedings of the CSU-EPSA, 2012, 24(1): 138-141.

[12] FRISCH K R. The logarithmic potential method for convex programming[R]. Norway: Institute of Economics, University of Oslo, 1955.

[13] WEI H, SASAKI H, YOKOYAMA R. An interiorpoint nonlinear programming for optimal power flow problems with a novel data structure[J]. IEEE Transactions on Power Systems, 1998, 13(2): 870-877.

[14] DEHDARI V, OLIVER D S, DEUTDCH C V. Comparison of optimization algorithms for reservoir management with constraints: a case study[J]. Journal of Petroleum Science and Engineering, 2012, 100: 41-49.

[15] 廖怀庆， 刘东， 黄玉辉， 等. 考虑新能源发电与储能装置接入的智能电网供转能力分析[J]. 中国电机工程学报, 2012, 32(16): 9-16.

LIAO Huaiqing, LIU Dong, HUANG Yuhui, et al． Smart grid power transfer capability analysis considering integrated renewable energy resources and energy storage systems[J]. Proceedings of the CSEE, 2012, 32(16): 9-16.

CoordinatedControlofDistributedGenerationsBasedonOptimalPowerFlow

CHEN Baisen1, LIAO Qingfen1, LIU Dichen1, WANG Wenyi2, WANG Zhiyi3

(1. School of Electrical Engineering, Wuhan University, Wuhan 430072, Hubei Province, China;2. Central Southern China Electric Power Design Institute, Wuhan 430071, Hubei Province, China;3. Huangshi Power Supply Company of State Grid Corporation, Huangshi 435000, Hubei Province, China)

As a clean and efficient resource which has a wide variety of sources and a efficient using, distributed generation has a better way to solve the energy shorting, ruining the environment, resource allocation and other problems, and has good economy, which has become a important part of the building of future power systems and the development of source systems. But there still are some challenges and problems behind the huge benefits of distributed generation connecting to the grid, such as load forecasting, power flow variation, power quality, power fluctuation, etc. This paper proposes a coordinated control technology of distributed network to the connecting of distributed generation, which takes the operation cost as the objective function, and on the base of predicts of load and the output of distributed generation, according to the optimal power flow and the constraints, uses three optimal methods including the sequential quadratic regulation, interior point and genetic algorithm for simulation to obtain the optimal value of the objective function and the output of the corresponding distributed generation. Through the comparison of three different algorithms, the results show that the sequential quadratic regulation method can more effectively complete the optimization of the objective function and has quick convergence, which can effectively support the coordinated control technology of distribution network for distributed generation.

distributed generation; objective function; optimal power flow; coordinated control; optimal algorithm

国家电网公司科技项目(5211011400BT)

陈柏森

2017-07-02

陈柏森(1992—)，男，硕士研究生，主要研究方向为配电系统运行评估、综合能源系统，bschen@whu.edu.cn；廖清芬(1975—)，女，博士，副教授,主要研究方向为智能配电技术、电力系统稳定控制；刘涤尘(1953—)，男，博士，教授，博士生导师，研究方向为电力系统运行控制;王文怡(1991—)，女，硕士，主要研究方向为配电系统运行与控制、分布式能源；王志义(1963—)，男，学士，工程师，主要研究方向为智能配电技术、配电系统运行与维护。

(编辑 谷子)