NEW RECURRENCE FORMULAE FOR THE POLYLOGARITHM FUNCTION

HE Yuan,ZHANG Jia-ling

(School of Science,Kunming University of Science and Technology,Kunming 650500,China)

NEW RECURRENCE FORMULAE FOR THE POLYLOGARITHM FUNCTION

HE Yuan,ZHANG Jia-ling

(School of Science,Kunming University of Science and Technology,Kunming 650500,China)

In this paper,we perform a further investigation for the polylogarithm function at negative integral arguments.By applying the generating function methods and Padé approximation techniques,we establish some new recurrence formulae for this type function and present some illustrative special cases of main results.

polylogarithm function;generating function;Padé approximants;recurrence formulae

1 Introduction

Letsandzbe complex numbers,the polylogarithm function Lis(z)is de fined by means of the Dirichlet series

which is valid for arbitrary complex ordersand for all complex argumentszwith|z|＜1 and can be extended to|z|≥1 by the process of analytic continuation.

The polylogarithm function at zero and negative integral arguments are referred to as the polypseudologarithms(or polypseudologs)of ordernby Lee[8].It is worth noticing that the values of polypseudologrithms atz=1 are related to the values of the Riemann zeta functionζ(s)at negative integers and are expressed in terms of the Bernoulli numbersBn,as follows(see,e.g.,[4,8])

In[11],Truesdell gave a closed formula for the polypseudologarithms,as follows

whereS(n,k)is the familiar Stirling numbers of the second kind.In[6],Eastham showed that there is no pure recurrence relation of the form

wherenis a positive integer,r≥nis allowed.TheAn(z)are algebraic functions ofzandA0(z)is not identically zero.More recently,Cvijović[5]discovered some similar ones for the polypseudologarithms to formula(1.3),and also established a new type closed formula for the polypseudologarithms in the following way

where[x]denotes the greatest integer≤xandT(n,k)is the tangent numbers(of orderk)or the higher order tangent numbers given by(see,e.g.,[3])

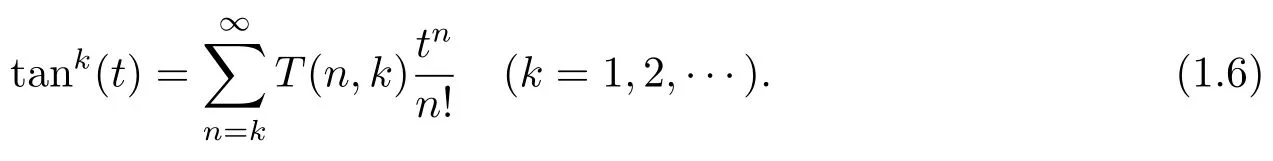
Motivated by the work of Eastham and Cvijović,in this paper we perform a further investigation for the polylogarithm function at negative integral arguments,and establish some new recurrence formulae for this type function to state that there exist some explicit recurrence relations of form(1.4)for the polypseudologarithms by applying the generating function methods and Padé approximation techniques.And we accordingly consider some illustrative special cases as well as immediate consequences of the main results.

2 Padé Approximants

We begin by recalling the de finition of Padé approximation to general series and their expression in the case of the exponential function.Letm,nbe non-negative integers and letPkbe the set of all polynomials of degree≤k.Given a functionfwith a Taylor expansion

in a neighborhood of the origin,a Padé form of type(m,n)is a pair(P,Q)satisfying that

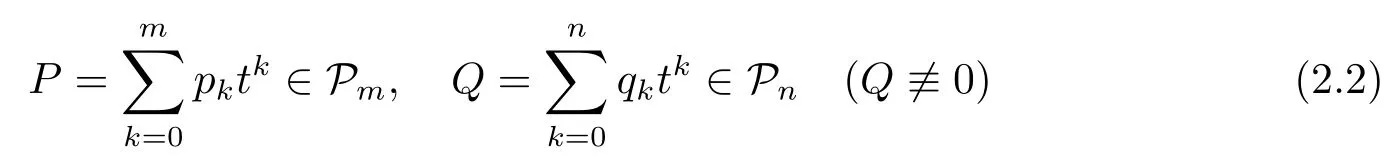
and

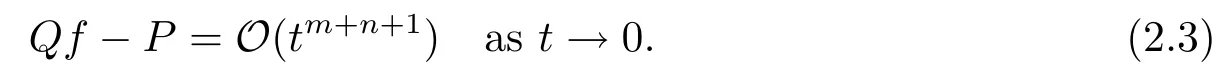
It is clear that every Padé form of type(m,n)forf(t)always exists and obeys the same rational function.The uniquely determined rational functionP/Qis called the Padé approximant of type(m,n)forf(t),and is denoted by[m/n]f(t)orrm,n[f;t],see for example,[1,2].

The study of Padé approximants to the exponential function was initiated by Hermite[7]and then continued by Padé[9].Given a pair(m,n)of nonnegative integers,the Padé approximant of type(m,n)foretis the unique rational function

with the property that

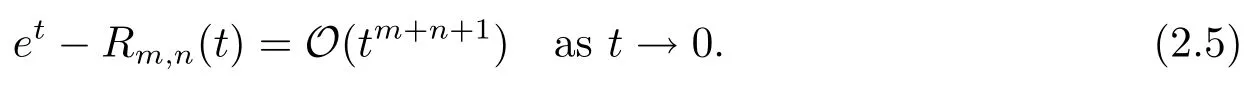
Unlike Padé approximants to other functions,it is possible to determine explicit formulae forPm,nandQm,n(see,e.g.,[10,p.245])

and

We here refer respectively toPm,n(t)andQm,n(t)as the Padé numerator and denominator of type(m,n)foret.In next section,we shall use the above Padé approximation to the exponential function to establish some new recurrence formulae for the polylogarithm function at zero and negative integral arguments.

3 The Restatements of Results

In[4],Cvijović discovered some similar formulae to(1.3)by making use of the following generating functions for the polypseudologarithms(see,e.g.,[11,12])

and

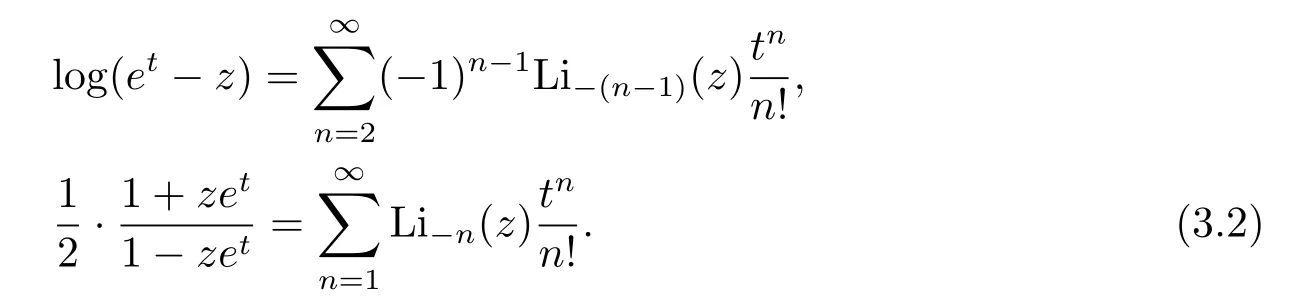
We shall replace the exponential functionetnot by its Taylor expansion aroundt=0 but by its Padé approximant in the generating function of the polypseudologarithms.We first rewrite the first formula of(3.1)as follows

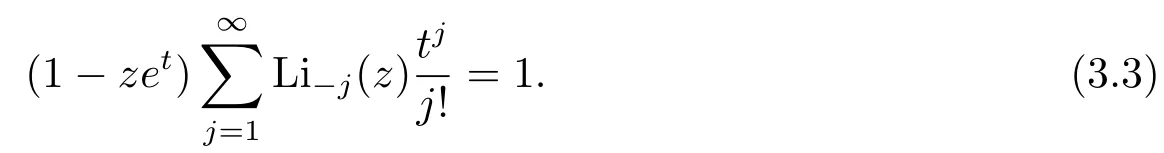
If we denote the right hand side of(2.8)bySm,n(t),the Padé approximant for the exponential functionetcan be expressed as

We now apply(3.4)to(3.3)and then obtain

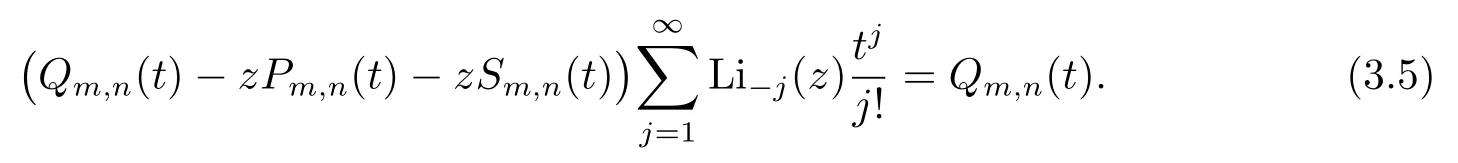
If we apply the exponential seriesin the right hand side of(2.8),with the help of the familiar beta function,we get

For convenience,we considerpm,n;k,qm,n;kandsm,n;kof the coefficients of the polynomialsPm,n(t),Qm,n(t)andSm,n(t)such that

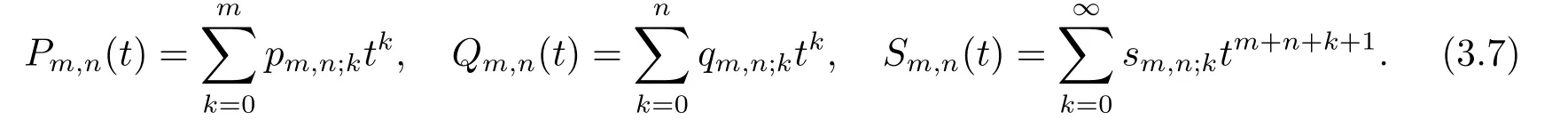
Obviously,the coefficientspm,n;k,qm,n;kandsm,n;kobey

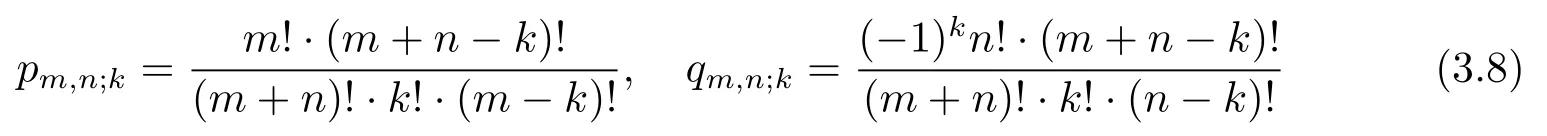
and

respectively.If we apply(3.7)to(3.5),we obtain

from which and the familiar Cauchy product,we discover

Comparing the coefficients oftlin(3.11)gives that for 1≤l≤m+n,

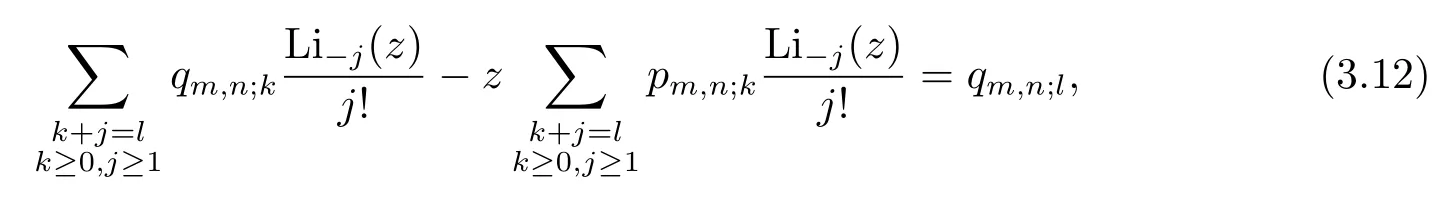
which together with(3.8)yields the following result.

Theorem 3.1Letl,m,nbe non-negative integers.Then for positive integerlwith max(m,n)＜l≤m+n,

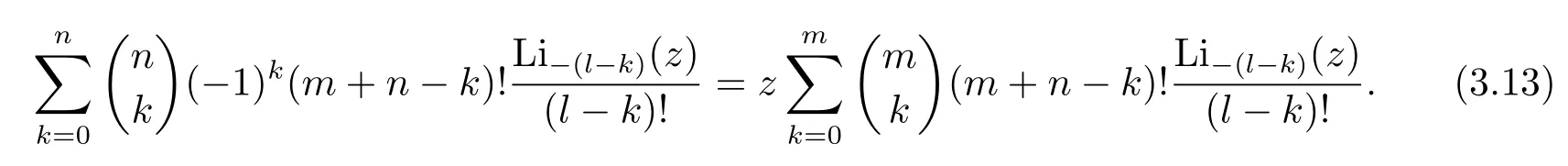
We next discuss some special cases of Theorem 3.1.Settingl=m+nin Theorem 3.1,we obtain that for positive integersm,n,

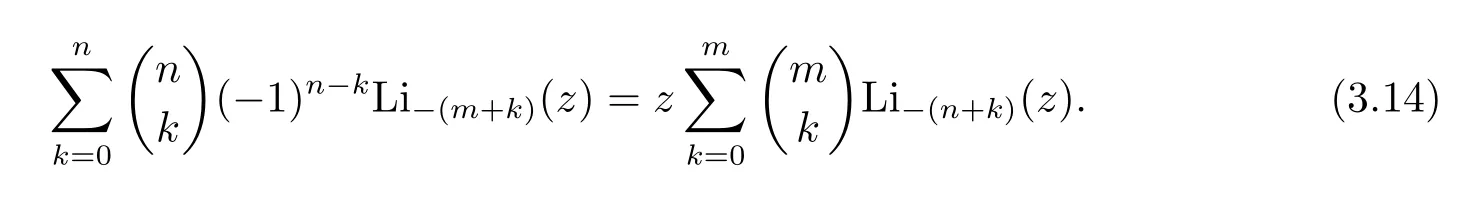
It is obvious that the casem=1 in(3.14)gives that for positive integern,

and the casen=1 in(3.14)arises

If we compare the coefficients oftlin(3.11)forl≥m+n+1,then

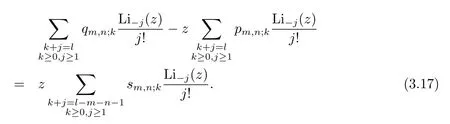
Hence applying(3.8)and(3.9)to(3.17)gives the following result.

Theorem 3.2Letm,nbe non-negative integers.Then for positive integerlwithl≥m+n+1,

It follows that we show some special cases of Theorem 3.2.Takingl=m+n+1 in Theorem 3.2,we obtain that for non-negative integersm,n,

In particular,the casem=0 in(3.19)arises

More generally,by settingm=0 andl=n+rin Theorem 3.2,we get that for non-negative integernand positive integerr,

And the casen=0 in(3.21)yields another recurrence formula to compute the values of the polypseudologarithms with Li0(z)=z/(1−z):

It becomes obvious that formulae(3.15),(3.16)and(3.22)mean that there exists pure recurrence relations of form(1.4)for the polypseudologarithms,respectively.

AcknowledgementThis work was done during the authors’visit for Department of Computer Science,State University of New York at Stony Brook.

[1]Baker Jr G A,Graves-Morris P.Padé approximants(2nd ed.)[M].Cambridge:Cambridge Univ.Press,1996.

[2]Brezinski C.History of continued fractions and Padé approximant[M].Berlin:Springer-Verlag,1991.

[3]Carlitz L,Scoville R.Tangent numbers and operators[J].Duke Math.J.,1972,39:413–429.

[4]Chen G H,Liu B L.Some identities related to the dedekind sums[J].J.Math.,2014,34:198–204.

[5]Cvijović D.Polypseudologarithms revisited[J].Phys.A,2010,389:1594–1600.

[6]Eastham M S P.On polylogarithms[J].Proc.Glasgow Math.Assoc.,1964,6:169–171.

[7]Hermite C.Sur lafonction exponentielle[J].C.R.Acad.Sci.Paris,1873,77:18–24,74–79,226–233,285–293.

[8]Lee M H.Polylogarithms and Riemann’sζfunction[J].Phys.Review E,1997,56:3909–3912.

[9]Padé H.Librairie scientifique et technique(edited by C.Brezinski)[M].Paris:A.Blanchard,1984.

[10]Perron O.Die Lehre von den Kettenbriichen(3rd ed.)[M].Stuttgart:Teubner,1957.

[11]Truesdell C.On a function which occurs in the theory of the structure of polymers[J].Ann.Math.,1945,46:144–157.

[12]Zeitlin D.Two methods for the evaluation ofAmer.Math.Monthly,1961,68:986–989.

关于polylogarithm函数新的循环公式

何 圆,张家玲
(昆明理工大学理学院,云南昆明 650500)

本文对polylogarithm函数在负整数点的情形作了进一步的研究.利用生成函数方法及Padé估计技巧,建立了此类函数的一些新的循环公式,并给出了主要结果的一些特殊情况.

polylogarithm函数;生成函数;Padé估计;循环公式

O156.4

11E41;33E20;05A19

A

0255-7797(2017)06-1154-07

date:2015-01-09Accepted date:2015-10-10

Supported by the Foundation for Fostering Talents in Kunming University of Science and Technology(KKSY201307047)and the National Natural Science Foundation of China(11326050;11071194).

Biography:He Yuan(1982–),male,born at Neijiang,Sichuan,associate professor,major in number theory and its applications.