涡激振动型水力复摆式压电俘能器的仿真与实验研究
宋汝君,单小彪,范梦龙,谢 涛
(1. 山东理工大学 机械工程学院,山东 淄博 255049;2. 哈尔滨工业大学 机电工程学院,哈尔滨 150001)
涡激振动型水力复摆式压电俘能器的仿真与实验研究
宋汝君1,单小彪2,范梦龙2,谢 涛2
(1. 山东理工大学 机械工程学院,山东 淄博 255049;2. 哈尔滨工业大学 机电工程学院,哈尔滨 150001)
针对低速水流的能量收集问题,提出了一种复摆式涡激振动压电俘能器。该俘能器由压电悬臂梁与尾端圆柱平行连接组成,具有免予封装绝缘,振动响应大,易于在低速水流中产生涡激共振等优点。通过流-固-电耦合仿真分析和实验测试的方法,研究了水流流速对复摆式压电俘能器振动和俘能的影响规律。结果发现,俘能器的输出功率随负载电阻先增大后减小,存在最优电阻可使俘能器的输出功率最大。俘能器的振动幅值和功率输出均随流速的增大而先增大后减小,在涡激共振处出现最大值;振动频率整体随着流速的增大而增大,但在涡激共振区域,由于“锁定”,俘能器的振动频率基本保持在俘能器的固有频率处。俘能器输出功率随圆柱直径的增大而增大,但涡激振动速度也相应的提高。
水流;涡激振动;压电俘能器;俘能
针对集成电路、微机电系统(Micro-Electro-Mechanical System,MEMS)和传感器等低能耗产品的供电问题,传统的供电方式(电池/电子)存在着环境污染、存储有限(需定期更换)等弊端。研究者需探究一种环境友好、持续的供能方式[1]。目前通过俘获环境振动能为电能的压电俘能方式得到了学者的重视。环境振动能分布广泛,有机械能、风动能、水动能等。其中水动能主要存在于河流、潮汐和海洋流等,他们的共同特点是分布广泛且多以低流速状态存在。因此,针对低速水流能量俘获技术是一项具有重大研究价值和学术意义的课题。
涡激振动常发生于低速水流环境中。利用涡激振动与压电俘能技术,可以转化低速水流动能为电能,即为涡激振动压电俘能技术[2]。Dai等[3-6]和Xie等[7]分别分析了尾端圆柱型压电俘能器和管状压电俘能器,获得了外接电阻、涡街脱落频率和来流速度等参数对振动响应、输出功率的相互关系。此外,针对横向梁尾端圆柱型俘能器的研究还有Akaydin等[8-9]。Gao等[10]在风洞中研究了倒立式涡激振动压电俘能器,为了忽略俘能器圆柱的重力影响,圆柱部分采用0.2 mm厚的相片纸制作。研究发现在5 m/s的风速情况下,该俘能器可获得30 μW的电能。对于低雷诺数的涡激振动压电俘能,Mehmood等[11]通过数值模拟分析了雷诺数为96≤Re≤118,外界负载为500 Ω≤R≤5 MΩ时,圆柱型涡激振动压电俘能器的振动俘能情况,发现外接负载对振动幅值、升力系数、输出电压和功率有很大影响,随着外接电阻的增大,共振区域增大。综上的研究主要是围绕气流进行,针对低速水流环境的压电俘能研究相对较少。
鉴于此,本文通过仿真和实验的方法研究了复摆式压电俘能器在低速水流环境中的涡激振动响应和俘能特性。首先通过建立俘能器的等效模型,然后采用Fluent®软件仿真分析俘能器的振动特点和能量输出大小,最后通过实验平台测试了俘能器的能量输出。
1 结构及模型设置
图1给出了复摆式压电俘能器涡激振动俘能的示意图。俘能器由单一压电梁和尾端圆柱组成,且尾端圆柱竖直立于来流中。圆柱产生涡激振动带动压电梁产生往复摆动,进而压电梁输出电能。

图1 复摆式涡激振动压电俘能器的结构示意图Fig.1 Structure diagram of the CPPEH with the VIV
该俘能器由压电梁和圆柱平行连接,形成I型结构,此俘能器具有以下优势:一方面I型结构有效的降低了俘能器本身的固有频率,能够使俘能器更容易在低水流环境中产生涡激共振;另一方面该俘能器除了受到流体的涡激力F(t)外,还存在一个涡激力矩M(t),故可以有效的增大俘能器的振动响应,提高发电能力。此外,俘能器仅圆柱浸入水中,不需要对压电梁进行封装绝缘处理,制作工艺简单。
基于建模的需要,提出如下假设条件:
① 基体与压电层紧固粘贴,不考虑黏合剂的影响;② 压电梁截面在变形前后均垂直于其中性面,且忽略沿压电梁中性面法向方向的应力;③ 压电层的电场强度垂直于板面,且沿厚度方向均匀分布;④ 将圆柱视为刚体,不考虑其变形;⑤ 由于复摆的角度较小,忽略由于复摆导致的圆柱浸水长度(未浸水长度)的变化。
在分析复摆式压电俘能器的模型时,应该考虑机电耦合效应。流体与圆柱之间也存在相互作用,所以俘能器建模时应当考虑流-固-电三个物理场之间的耦合。复摆式压电俘能器的单自由度模型的本构方程为
(1)
式中:M为等效质量;C为等效阻尼,表示为2Mωnξ;K为等效刚度;Θ为压电梁的等效机电耦合系数;V(t)为外接电阻两端电压;Cp为压电片等效电容;R为外接电阻;w(xa,t)为等效点A处在时间t时刻的横向位移;F(t)为流激力。本文的流-固-电三物理场耦合过程如下:① 在某一时刻t,通过Fluent®仿真平台计算流场,获得压电俘能器受到的涡激力F(t);② 利用流激力F(t),求解式(1),获得压电俘能器的位移w,速度dw/dt,加速度d2w/dt2和电压V(t);③ 根据位移w,更新流场网格,进入下一个时间步Δt,直到运算结束。
俘能器的输出功率表示为
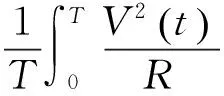
(2)
式中,T为输出电压的交变周期。
1.1等效刚度
本文中的压电梁为单晶梁,其截面如图1的右图所示。压电梁的宽度为b,压电层的厚度为hp,基体的厚度为hs。压电梁长度为l,圆柱的长度和未浸水长度分别为lc和ls。以压电梁的中性面为x轴建立如图1所示坐标系。压电层上表面的纵坐标为ha,压电层与基体的接触面的纵坐标为hc,则
ha=(hp+hs)/2,hc=(hs-hp)/2
(3)
则压电梁的抗弯刚度为
KEI=EI=EpIp+EsIs=
(4)
假设在点A受到一个力F(t)的作用,将该力作用点等效到压电梁末端,则可等效为一个力F(t)和一个力矩M(t)。对压电梁受力分析,如图1所示,即M(t)=F(t) (xa-l)。
在力F(t)作用下,压电梁的挠度曲线方程为
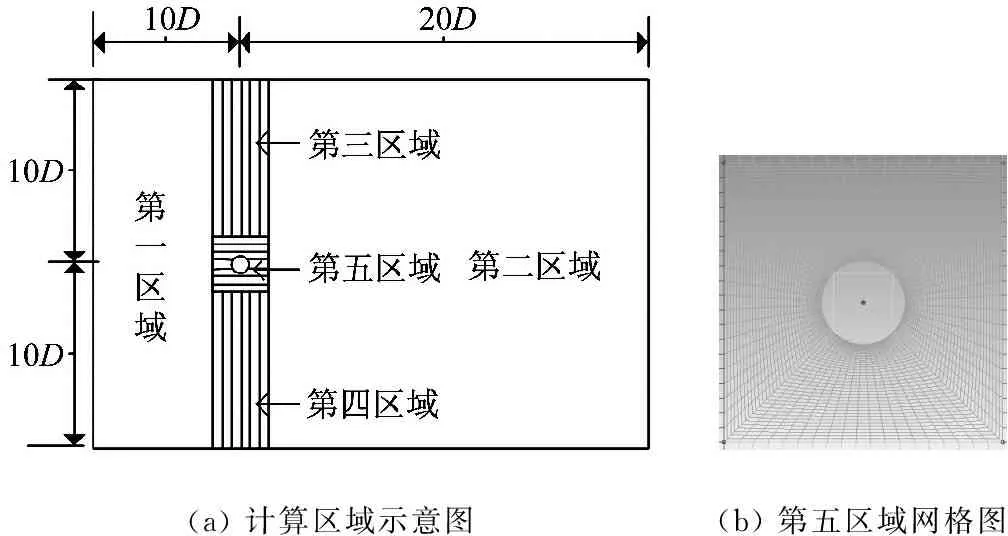
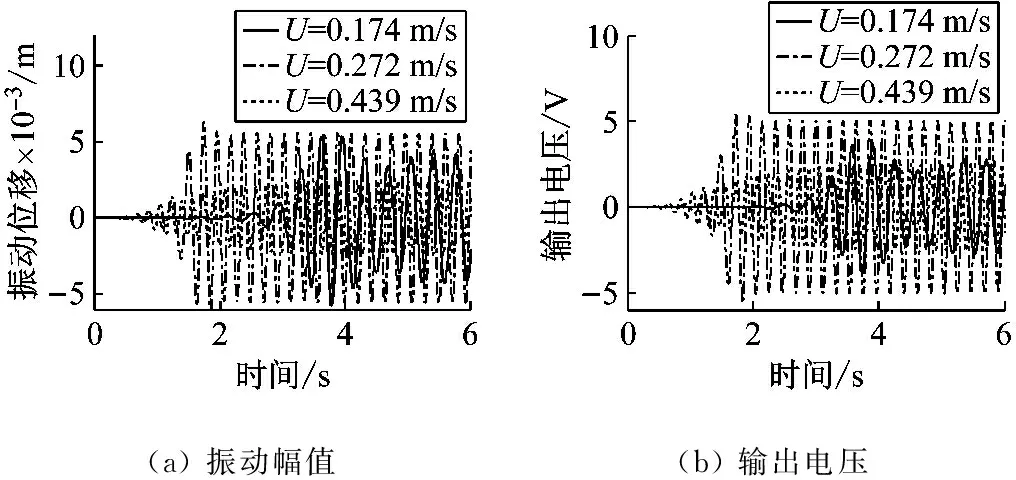
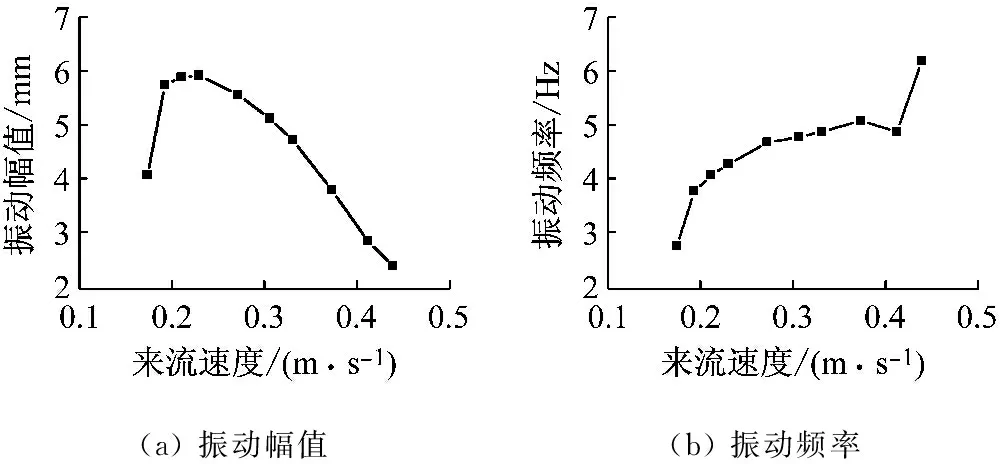
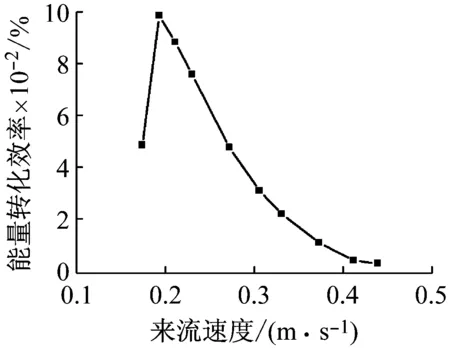
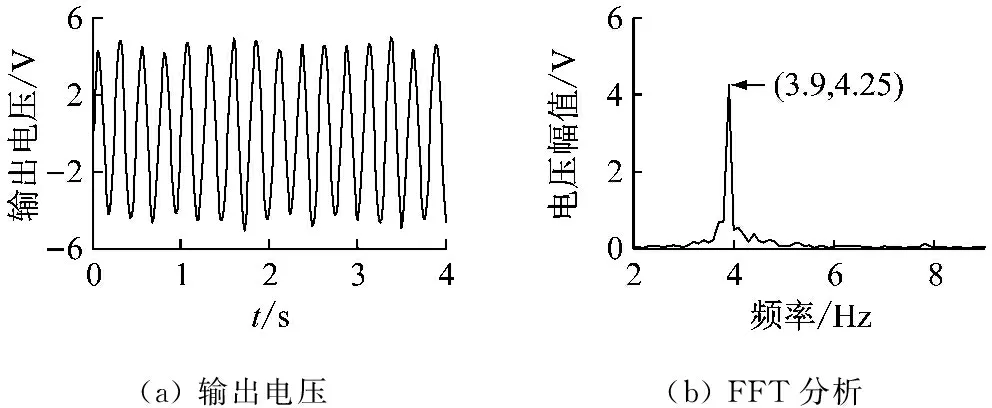
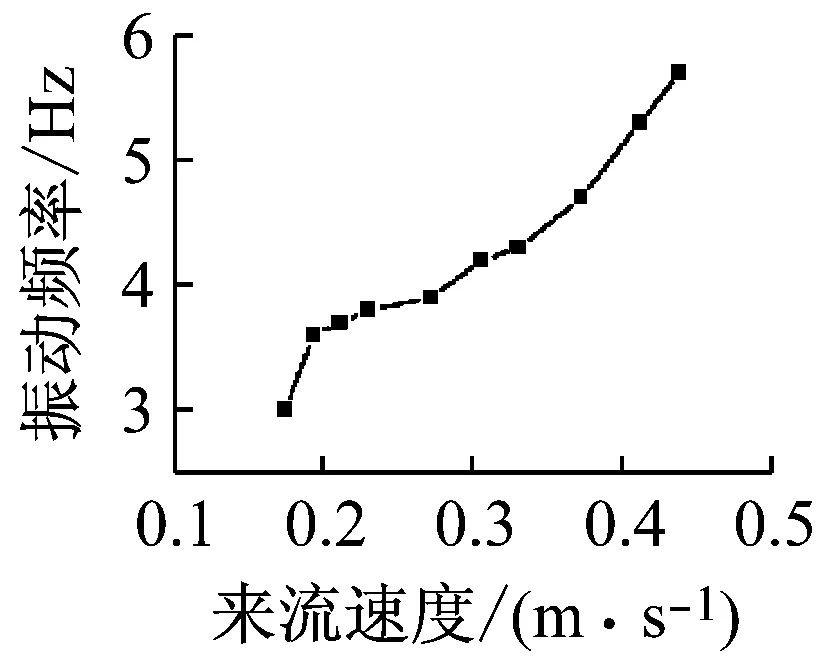
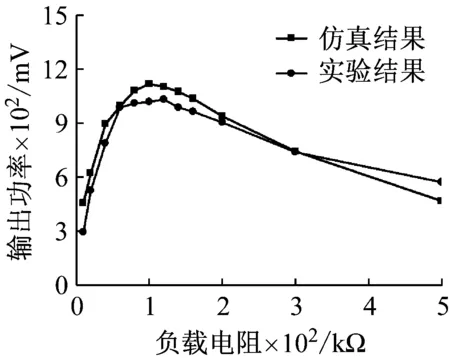
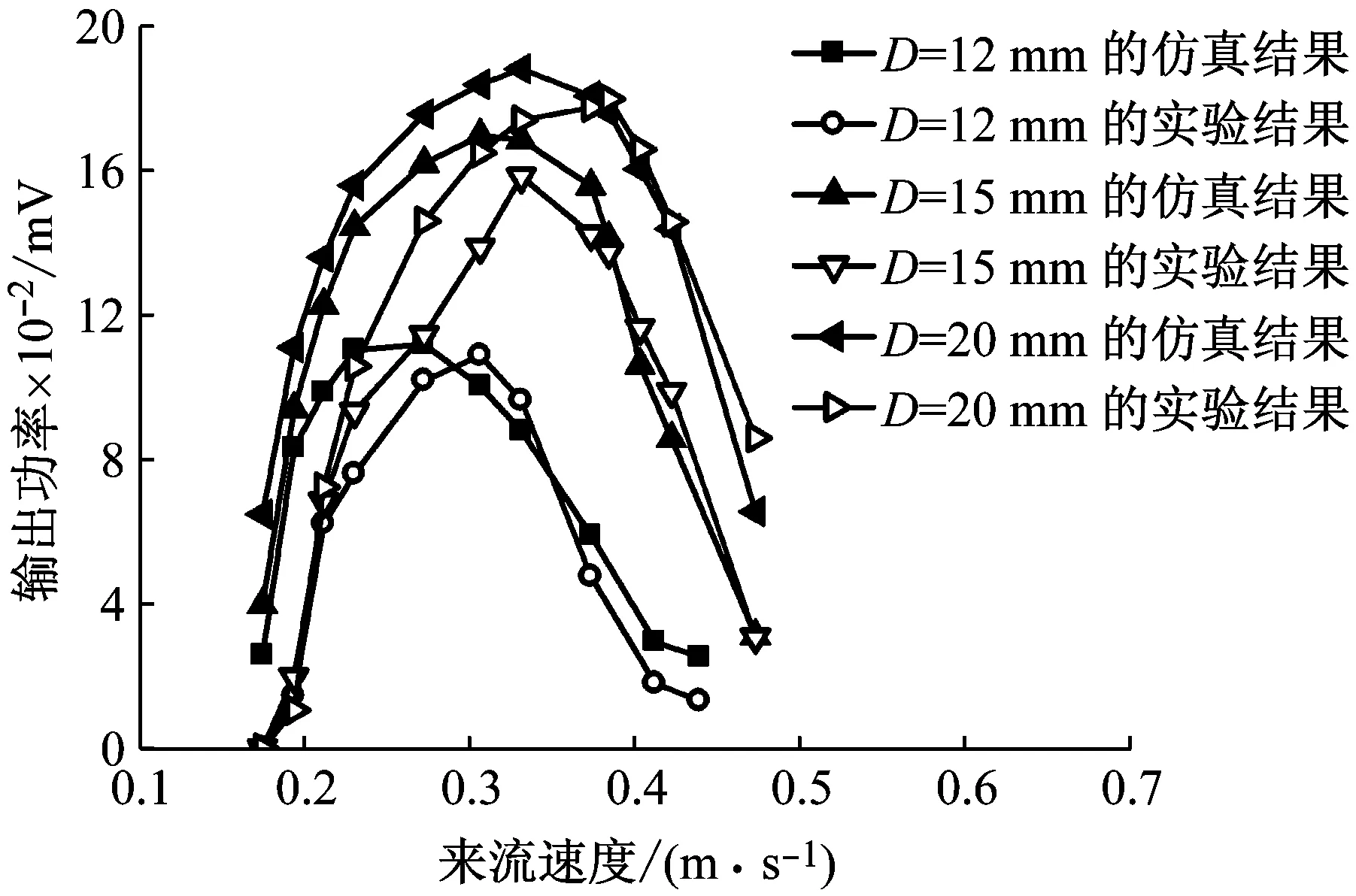
w1(x,t)=F(t)x2(3l-x)/(6KEI)x (5) 在力矩M(t)作用下,压电梁的挠度曲线方程为 w2(x,t)=M(t)x2/(2KEI)x (6) 由叠加定理可知,在力F(t)和力矩M(t)的作用下,压电梁的挠度表示为w(x,t)=w1(x,t)+w2(x,t)。 压电梁末端的转角为 θ=∂w(x,t)/∂x|x=l=F(t)l(2xa-l)/(2KEI) (7) 由于圆柱的变形相对于压电梁的变形而言非常小,所以可以将圆柱视为刚体。圆柱的位移如图1所示。则圆柱上距离压电梁固定端为x处的位移为 (8) 综上可知,单圆柱-俘能器系统在涡激力F(t)作用下的挠度曲线方程为 (9) 所以在涡激力F(t)的作用下,点A的位移为 (10) 根据胡克定律F=Kω(xa,t),则俘能器的等效刚度K表示为 (11) 1.2等效质量 将复摆式压电俘能系统转化为一阶质量-弹簧-阻尼系统,等效前后能量守恒。等效前原系统动能为压电层动能Tp、基层动能Ts、圆柱动能Tc和附加流体动能TM之和,表示为 T=Tp+Ts+Tc+TM (12) 其中, (13) 式中:Vp为压电层体积;Vs为基体体积;Vc为圆柱体积;Vw为圆柱浸入水中的体积,且φ(l)、φ(l)和γ(l)分别表示为 l4(3xa-l)2(lc-ls)+ (14) 设等效后的质量为M,等效点为点A,则等效后的动能为 (15) 其中, (16) 利用T=T*可得系统的等效质量为 (17) 1.3阻尼比与机电耦合系数 系统的结构阻尼比可通过自由振动响应曲线求得。为了得到复摆式压电俘能器的自由振动响应曲线,我们利用实验的方法,将复摆式压电俘能器按照实验的要求放于静止的水中,给圆柱施加一个脉冲力,然后记录压电片的输出电压。绘制压电片的输出电压曲线就可得到该系统的自由振动响应曲线,得到了系统的阻尼比见表 1所示。 压电梁的等效机电耦合系数表示压电梁将振动能转化为电能的能力,其计算公式为[12] (18) 由式(18)可知,压电梁的等效机电耦合系数与系统的开路和短路谐振频率有关。系统的开路和短路谐振频率可以用ANSYS®有限元仿真软件得到。根据表2在ANSYS®软件中建立复摆式压电俘能器的有限元模型如图2所示。 图2 压电俘能系统的有限元模型 压电梁上的压电层采用SOLID5单元模拟,压电梁上的基体以及梁末端的圆柱采用SOLID45单元模拟,外电路的负载电阻采用CIRCU94单元模拟。用命令流对各电极层的电压自由度进行连接,使各电极面上每一个节点的电势相等。压电片的上表面上的节点与公共节点“1”耦合,压电片的下表面上的节点与公共节点“2”耦合,公共节点“1”和“2”与外负载电阻R连接。当R分别为R→0和R→∞时,可以分别得到系统的开路谐振频率和短路谐振频率,得到了系统的开路和短路谐振频率见表 1所示。压电片的等效电容的计算式为Cp=bεTl/hp=3.34×10-7F,由式(18)可得Θ=4.31×10-4N/V。 1.4模型设置 压电梁的压电层选用PZT-5H压电陶瓷,基层为纯铝材质,圆柱采用亚克力材料制作。表 1给出了不同圆柱直径下的阻尼比、开路短路谐振频率大小。表2给出了的压电俘能器的结构与材料参数。 表1 不同圆柱直径下的参数取值Tab.1 Parameters of the harvester for different cylinder diameters 表2 俘能器结构参数和材料属性Tab.2 Structure parameters and material properties of the harvester 2.1仿真设置 本文运用Fluent®软件模拟流场,计算圆柱的流体力,利用式(1)和式(2)编写UDF程序,分析俘能器振动和俘能特性。根据圆柱的涡激振动特点,选用动态层模型动网格方法模拟涡激振动。计算域如图3 (a)所示,大小为20D×30D,圆柱重心距离入口和出口分别为10D和20D,距离上下边界均为10D。为了提高计算精度,将计算区域分为五个部分。第一、二区域为静止网格;第三、四区域为动态层网格;第五区域为刚性边界网格,计算时刚性边界网格随圆柱区域一同运动以确保界面附近网格质量。采用k-ω模型中的SST湍流模型求解。文中采用结构网格,且圆柱周围设置膨胀层,第一层厚度为1×10-6m,膨胀系数为1.1,划分的网格图如所示图3 (b)。 (a)计算区域示意图(b)第五区域网格图 2.2仿真结果 首先取圆柱直径为12 mm,负载电阻为100 kΩ,研究不同流速下俘能器的振动响应。图4给出了在流速分别为0.174 m/s、0.272 m/s和0.439 m/s时压电俘能器圆柱体的振动位移和输出电压随时间的变化曲线。可知在水流的作用下,俘能器由静止逐渐产生振动,且振动幅值逐渐增大,最后趋于稳定状态。俘能器的振动位移和输出电压的变化频率随着流速的增大而增大,输出电压随着振动幅值的变化而变化。流速为0. 272 m/s时,俘能器的振动幅值和输出电压均大于流速为0.174 m/s和0. 439 m/s时。 (a)振动幅值(b)输出电压 进一步深入分析流速对振动响应的影响,通过统计多个流速下俘能器的振动响应结果,得到了如图5所示的振动幅值和振动频率随来流速度的变化曲线。 由图5可知:俘能器的振动幅值随来流速度的增大而先增大后减小;振动频率随着来流速度的增大整体呈增大趋势,但由于涡激振动的“锁定”现象,俘能器在流速为0.193~0.412 m/s的范围内,振动频率基本固定在4~5 Hz附近,且此区域内与俘能器的固有频率相近,俘能器产生涡激共振。 (a)振动幅值(b)振动频率 能量转化效率是评估压电俘能器的俘能性能的一项重要指标,是发电功率与水流提供的输入功率的比值,表示为 (19) 式中:Pout为俘能器的输出功率;Pin为水流提供的输入功率,表示为 (20) 式中:A为俘能器振动幅值;U为来流速度。 图6给出了圆柱直径为12 mm时,压电俘能器的能量转化效率随流速的变化情况。由图可知,能量转化效率随来流速度的增大而先增大后减小,在0.193 m/s处获得最大值(0.098 5%),此处为俘能器发生涡激共振的初始阶段,如图5所示。 图6 俘能器能量转化效率随流速的变化Fig.6 Energy exchange efficiency of harvester versus water velocity 根据表 1和表2给出的压电俘能器结构尺寸制作实验样机,利用如图7所示实验平台对俘能样机进行流激振动实验。实验平台是一个明渠闭环水槽系统,由水槽、进水管、出水管和离心水泵组成。其中水槽由蜂窝器、三层阻尼网、收缩段和实验段组成。蜂窝器和阻尼网是为了破碎水流涡旋和降低水流的湍流度;收缩段是为了提高水流稳定性和均匀性。实验段设计尺寸为1 200 mm×400 mm×250 mm。水流的流量和流速由离心泵调节,而离心泵由变频器调节。压电俘能器由夹具固定于水槽壁面上,且使尾端圆柱浸入水中。在水流的激励下,压电俘能器产生振动并输出电压。电压信号由NI数据采集卡(NI 9229)采集,并输入计算机实时显示和存储。 图7 涡激振动俘能实验系统图Fig.7 Experimental system of energy harvesting with the VIV 基于图7所示的实验系统,实验测试了压电俘能器在低速水流下(0.1~0.5 m/s)的能量输出特性。为了与仿真分析结果对比,首先给出了俘能器圆柱直径为12 mm,流速为0.272 m/s,负载电阻为100 kΩ时,输出电压随时间的变化曲线及其FFT分析图,如图8(a)和图8(b)所示,进而整理各个流速下的振动频率值,得到了俘能器振动频率与流速的关系图,如图8(c)所示。 (c) 振动频率随流速的变化图8 实验测得俘能器输出电压随时间的变化曲线及其FFT分析Fig.8 Output voltage of experimental study versus time and its FFT analysis 由图8可知,实验电压同样为交变电压。电压变化情况反映了压电俘能器的振动情况,故可知压电俘能器此时的振动频率为3.9 Hz,峰峰值电压为4.25 V。对比图5(b)和图8(c)可知,俘能器的振动频率随来流速度的变化规律与仿真结果相近。进一步分析负载电阻和来流速度对俘能器输出功率的影响。图9给出了圆柱直径为12 mm和流速为0.272 m/s时俘能器输出功率随负载电阻的变化曲线。由图可知,俘能器的输出功率随着负载电阻的增大而先增大后减小,存在一个电阻值使俘能器输出功率最大,即最优电阻值。 图9 压电俘能器输出功率随负载电阻的变化Fig.9 Output power of the CPPEH versus load resistance 图10给出了负载电阻为100 kΩ时压电俘能器在不同圆柱直径下输出功率随流速变化情况。由图可知,压电俘能器的输出功率随来流的增大而先增大后减小,在涡激共振处输出功率最大。当圆柱直径为12 mm时,在0.3 m/s附近获得最大值,即为压电俘能器的涡激共振处。仿真分析得到俘能器在流速为0.272 m/s处获得最大极值(0.116 mW),而实验测试发现压电俘能器在流速为0.306 m/s处可产生0.109 mW的功率。当圆柱直径分别为15 mm和20 mm时,涡激共振发生在0.355 m/s和0.384 m/s附近,实验测得的最大输出功率分别为0.158 3 mW(0.355 m/s处)和0.179 7 mW(0.384 m/s处)。对比圆柱直径对输出功率的影响发现:随着圆柱直径的增大,输出功率增大,但同时产生涡激共振的速度也相应的增大。 图10 不同圆柱直径下输出功率随流速的变化曲线Fig.10 Output power of the harvester versus water velocity for different cylinder diameters 对比仿真和实验结果,发现数值分析结果与实验测试结果有一定的误差,仿真获得的涡激振动流速均略小于实验测试结果,而最大值均略大于实验结果。误差分析如下:① 理论建模过程中,为了简化建模过程,采用了一定的假设条件;② 仿真分析过程中,由于网格划分情况,数值计算方法等因素,存在一定的数值计算误差。③ 实验测试过程中,包括压电片参数的测试、水流流速的测量、输出电压的采集、电压数据的数值处理等过程均会存在一定的误差,尤其水流流速的测量的误差会较大,因为水流的波动性难以控制。此外,理论建模过程中,假设为均匀层流;而实验过程中,尽管实验水槽做了一定的稳流处理,如蜂窝器、阻尼网以及收缩段,但流场仍然会受到水槽壁面、水泵振动影响,导致实验测试过程中的流场分布依然复杂。 本文研究了一种面向低速水流的复摆式涡激振动压电俘能器,该俘能器具有免予封装绝缘、振动响应大、固有频率低等优点,易于低速水流中产生涡激共振,提高发电性能。通过耦合流-固-电三物理场的仿真分析和流激振动的实验测试,分析了俘能器涡激振动响应和能量输出特点。研究表明,复摆式压电俘能器的振动幅值和输出功率随着流速的增大而先增大后减小,在涡激共振时振动幅值和输出功率最大。压电俘能器的最大能量转化效率发生在涡激共振的初始阶段。振动频率整体随着流速的增大而增大,但由于涡激振动的“锁定”现象,在涡激共振区域,振动频率维持在俘能器的固有频率处。俘能器的输出功率随着负载电阻的增大而先增大后减小,存在最优电阻使输出功率最大。输出功率随着圆柱直径的增大而增大,但产生涡激振动的水流速度也相应的增大。因此,在低速水流环境下应该合理选取圆柱直径,既要适当增大圆柱直径以提高功率输出又要保证俘能器能够产生涡激共振。 [1] 袁江波, 谢涛, 单小彪,等. 压电俘能技术研究现状综述[J]. 振动与冲击, 2009,28(10):36-42. YUAN Jiangbo, XIE Tao, SHAN Xiaobiao, et al. A review of current situation for piezoelectric energy harvesting[J]. Journal of Vibration and Shock, 2009,28(10):36-42. [2] SONG Rujun, SHAN Xiaobiao, LÜ Fengchi, et al. A novel piezoelectric energy harvester using the macro fiber composite cantilever with a bicylinder in water[J]. Applied Sciences, 2015,5(4):1942-1954. [3] DAI Huliang, ABDELKEFI A, WANG Lin. Piezoelectric energy harvesting from concurrent vortex-induced vibrations and base excitations[J]. Nonlinear Dynamics, 2014,77(3):967-981. [4] DAI Huliang, ABDELKEFI A, WANG Lin. Theoretical modeling and nonlinear analysis of piezoelectric energy harvesting from vortex-induced vibrations[J]. Journal of Intelligent Material Systems and Structures, 2014,25(14):1861-1874. [5] DAI Huliang, ABDELKEFI A, YANG Y, et al. Orientation of bluff body for designing efficient energy harvesters from vortex-induced vibrations[J]. Applied Physics Letters, 2016,108(5):053902. [6] DAI Huliang, ABDELKEFI A, WANG Lin, et al. Time-delay feedback controller for amplitude reduction in vortex-induced vibrations[J]. Nonlinear Dynamics, 2014,80(1/2):59-70. [7] XIE Jinmin, YANG Jiashi, HU Hongping, et al. Piezoelectric energy harvester based on flow-induced flexural vibration of a circular cylinder[J]. Journal of Intelligent Material Systems and Structures, 2011,23(2):135-139. [8] AKAYDIN H D, ELVIN N, ANDREOPOULO Y. The performance of a self-excited fluidic energy harvester[J]. Smart Materials and Structures, 2012,21(2):025007. [9] WANG Junlei, RAN Jingyu, ZHANG Zhien. Energy harvester based on the synchronization phenomenon of a circular cylinder[J]. Mathematical Problems in Engineering, 2014(2014):1-9. [10] GAO Xiaotong, SHIH W H, SHIH W Y. Flow energy harvesting using piezoelectric cantilever with cylindrical extension[J]. IEEE Transactions on Industrial Electronics, 2013,60(3):1116-1118. [11] MEHMOOD A, ABDELKEFI A, HAJJ M R, et al. Piezoelectric energy harvesting from vortex-induced vibrations of circular cylinder[J]. Journal of Sound and Vibration, 2013,332(19):4656-4667. [12] ZHAO Liya, TANG Lihua, YANG Yaowen. Comparison of modeling methods and parametric study for a piezoelectric wind energy harvester[J]. Smart Materials & Structures, 2013, 22(12):125003-125014. Simulationsandexperimentsonahydrodynamiccompoundpendulumpiezoelectricenergyharvesteraccompaniedwithvortex-inducedvibration SONG Rujun1, SHAN Xiaobiao2, FAN Menglong2, XIE Tao2 (1. School of Mechanical Engineering, Shandong University of Technology, Zibo 255049, China;2. School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China) A compound pendulum piezoelectric energy harvester (CPPEH) accompanied with vortex-induced vibration (VIV) was proposed to convert the water flow energy to electricity. The harvester was composed of a piezoelectric cantilever beam and a parallel cylinder, which has the advantages of exempting from encapsulation insulation, greater vibration response and being easy to generate vortex-induced resonance in low-speed water flow. The effects of water velocity on the hydrodynamic response and energy harvesting performance of the CPPEH were investigated by virtue of the simulation analysis on the fluid-structure-electric coupling and experimental tests. It is found that the output power first increases as the load resistance increases, the maximum power output is obtained when reaching the optimal resistance, and then the output power decreases. The vibration amplitude and output power have the same changing relation with the flow velocity and the maximum power output is obtained at the vortex-induced resonance. The vibration frequency is overall increasing with the increase of the flow velocity. However, because of the “lock-in” of the vortex-induced vibration, the vibration frequency is mainly equal to the natural frequency of the CPPEH during the vortex-induced resonance. The output power of the harvester is enhanced with the increase of cylinder diameter, while the vibration velocity of the vortex-induced resonance is increased at the same time. water flow; vortex-induced vibration; piezoelectric energy harvester; energy harvesting TN384; TP211 A 10.13465/j.cnki.jvs.2017.19.012 国家自然科学基金资助项目(51677043;51705296);山东省自然科学基金资助项目(ZR2017BEE039) 2016-05-11 修改稿收到日期:2016-07-13 宋汝君 男,博士,讲师,1988年9月生 谢涛 男,博士,教授,博士生导师,1965年2月生E-mail:xietao@hit.edu.cn

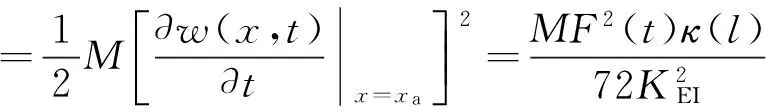
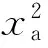
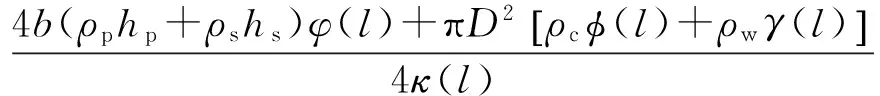
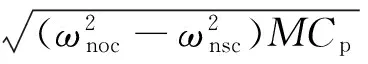

Fig.2 Finite element model of the CPPEH

2 仿真设置及分析
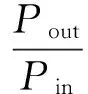
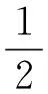
3 实验研究

4 结 论

