序列卷积和计算新方法
井敏英, 龙姝明
(陕西理工大学 物理与电信工程学院, 陕西 汉中 723000)
序列卷积和计算新方法
井敏英, 龙姝明
(陕西理工大学 物理与电信工程学院, 陕西 汉中 723000)
求卷积和是在时域中计算离散线性时不变系统响应的重要方法,但长序列卷积和计算的时间复杂度和空间复杂度都很高,实现计算时需要极大内存的计算机系统,而且计算耗时很长。针对这一问题,提出计算长序列卷积和的无数据移动的矢量标积算法,并且在MATLAB环境中编程实现了算法。研究发现,无数据移动的矢量标积算法明显地降低了长序列卷积和计算的空间复杂度和时间复杂度。用无数据移动的矢量标积算法编程,在小内存计算机系统上可以快速计算长序列卷积和。
线性时不变系统; 序列; 卷积和; 矢量标积; MATLAB程序
线性时不变(Linear Time-Invariant,LTI)系统理论应用非常广泛[1]。离散LTI系统对输入信号(序列)的响应,在时域中计算的步骤是,先计算系统的单位脉冲响应(序列),再计算输入信号(序列)与单位脉冲响应(序列)的卷积和[2]。文献[3-8]给出了卷积和计算的解释,文献[9-10]讨论了卷积的应用。但是这些方法计算的空间复杂度高,长序列卷积和计算在小内存计算机系统上很难实现。事实上,长序列卷积和计算是信号处理的难题。
本文对几种流行的序列卷积和计算方法进行了研究,分析了各自的优缺点,通过深入研究提出了序列卷积和计算的无数据移动的矢量标积新算法。此算法计算空间复杂度极低,时间复杂度相对现有部分算法明显有所降低。无数据移动的矢量标积算法使得长序列卷积和的计算在一般PC机上很容易编程实现。
1 三种常用的序列卷积和计算方法特点
长序列卷积和计算的解析法与图解法,本质上是依据序列卷积和定义进行计算。
方法一:按卷积和定义计算两序列卷积和。
设x(k)和y(k)长度分别为n和m,k=0,1,…,n+m-2,其卷积和定义为
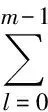
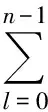
(1)
显见,可以用多次乘法和加法计算两序列的卷积和。
卷积和计算耗时近似为4n·m次乘法耗时(包含n·m次乘法、n·m次加法、n·m次数值比较和n·m次逻辑判断所花费的时间代价),计算占用存储空间16(n+m)字节。
方法特点:时间复杂度极高,空间复杂度很低,编程实现有点难度。
方法二:将两序列转换为矩阵,利用矩阵乘法完成序列卷积和计算。
我们以x(k)={a,b}和y(k)={u,v,w}为例说明用矩阵乘法计算x(k)与y(k)的卷积和。考虑到两序列卷积和长度为2+3-1=4,首先由较长序列{u,v,w}构造4列2行矩阵,可通过给较长序列末尾补零得到矩阵第一行,补零个数等于较短序列的长度减1,在这里补零个数为2-1=1,然后循环右移一个数据存储位置得到第二行,依次类推来构造较长序列对应的矩阵,矩阵的行数与较短序列长度相同。最后将较短序列看成单行矩阵左乘较长序列对应矩阵,即得到两序列卷积和的结果序列。计算过程如下:
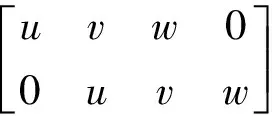
(2)
如果两序列长度分别为n和m(设n≤m),则采用矩阵乘法算法计算序列卷积和要完成的乘法和加法次数均为2n(n+m)次(含构造矩阵时在内存中多次循环移动数据消耗的时间代价)。计算需要内存8((n+1)·m+2n)字节。
方法特点:算法的空间复杂度非常高,时间复杂度较低,编程难度很低,易理解。
方法三:利用快速傅里叶变换计算卷积和。
设要用快速傅里叶变换(FFT)计算长度为n和长度为m的两序列x(k)和y(k)的卷积和,计算步骤是:
(1)给序列x(k)末尾补m-1个0成为序列x0,给序列y(k)末尾补n-1个0成为序列y0;
(2)分别对x0和y0取FFT得到复数频率序列X和Y;
(3)计算频域序列X和Y的数组乘法Z=X·Y(即对应位置元素相乘);
(4)计算复数序列Z的逆傅里叶变换(IFFT),得到x(k)与y(k)的卷积和。
可用(3)式描述计算步骤
X=FFT[x0],Y=FFT[y0],Z=X·Y,x(k)*y(k)=IFFT[Z],
(3)
设N=n+m-1,采用FFT算法计算两序列卷积和,需要完成4N(1+3log2N)次实数乘法和加法,耗时代价近似为8N(1+3log2N)次实数乘法的耗时,计算需要的内存大约为64N字节。
方法特点:时间复杂度极低,空间复杂度高于定义法又远低于矩阵乘法,编程简单,但初学者理解卷积和计算过程比较困难。
上述计算卷积和的3种算法,方法一适合理论教学,无工程实践价值;方法二用于长序列卷积和计算非常困难,不能用于实践;方法三计算长序列卷积和最快,有实践应用价值,但即便是短序列卷积和,手工计算也极其困难。我们期盼寻求长或短序列卷积和计算都很快、很省空间、又易于理解的卷积和计算方法。研究发现,无数据移动的矢量标积算法就是我们期盼的卷积和计算新方法。
2 序列卷积和计算的新方法——无数据移动的矢量标积算法
设要计算长度为n和长度为m的两序列x(k)和y(k)的卷积和(设n≤m),深入研究发现,用无数据移动的矢量标积算法,可以快速计算序列卷积和,计算步骤是:
(1)将较短序列x的数据位置反序得到xf;
(2)将较长序列y首尾都放置n-1个0数据,创建一个长度为m+2n-2的序列yoo;
(3)设j=1,2,…,n+m-1,从yoo的第j个位置开始顺序取出n个数据记为yoo(j:j+n-1),与xf做矢量标积给出卷积和结果的第j个数据,这一步需要重复计算n+m-1次,即
z=x*y,z(j)=xf·yoo(j:j+n-1),j=1,2,…,n+m-1。
(4)
在MATLAB 2012a软件环境下,具体计算步骤如下(其中含有程序语句):
(1)计算两序列长度并将第一序列反序再转置为列矢量
n=length(x); m=length(y); L=n+m-1; xf=x(n:-1:1)′ ;
(2)给y前后各补n-1个0存于yoo中
yoo=zeros(1,L+n-1); yoo(n:L)=y;
(3)从yoo的第j个位置开始取n个数据与xf做矢量标(或点)积运算,作为卷积计算结果的第j个数据z(j),j=1,…,L,重复做L次标(或点)积运算完成卷积和计算,
for j=1:L; z(j)=yoo(j:j+n-1)*xf; end %此处的*代表矢量标积运算
以序列x={a,b}(n=2)与序列y={u,v,w}(m=3)为例,演示无数据移动的矢量标积算法计算卷积和的手动步骤:
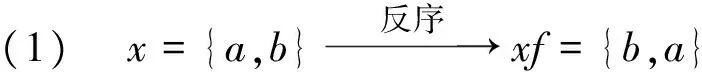
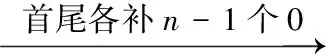
(3) {0,u,v,w,0}
{b,a}z(1)={b,a}·{0,u}=au
{b,a}z(2)={b,a}·{u,v}=bu+av
{b,a}z(3)={b,a}·{v,w}=bv+aw
{b,a}z(1)={b,a}·{w,0}=bw
顺序从首尾都补0的序列中取n个数据与xf做矢量标量积得到两序列的卷积和,即
z=x*y={au,bu+av,bv+aw,bw}。
特别注意,这里讨论的矢量标积算法编程实现时,不需要在内存中移动数据,因为移动数据是要耗时耗能的举动,正因为这样称新方法为无数据移动的矢量标积算法。
采用“无数据移动的矢量标积”算法计算两长序列的卷积和,需要完成n(n+m-1)次实数乘法和加法,耗时代价近似为2n(n+m)次实数乘法的耗时,计算需要的内存为16(m+2n)字节。
例估计用无数据移动的矢量标积算法对30 min单声道录音数据进行滤波的时空复杂度。
如果用无数据移动的矢量标积算法编程计算卷积和来完成对声音数据进行滤波(注意n=1024,m=22 050×1800),要完成的乘法次数为2n(n+m)= 8.13×1010次,计算过程需要内存16(m+2n)=0.64 GB。相对于卷积和定义法算法,无数据移动的矢量标积算法的时间复杂度至少降低50%,但空间复杂度没有变化。在一般PC机上,这一声音滤波的无数据移动的矢量标积算法非常容易实现,因此该方法既可以用于教学(易于理解)又可以用于工程实践解决信号滤波问题。
无数据移动的矢量标积算法特点:时间复杂度和空间复杂度都相对较低,易于理解易于编程实现,既可用于短序列卷积和的手工计算,又可以用于长序列卷积和的编程上机计算。
3 长序列卷积计算方法时间复杂度实验比较
为了定量比较卷积和的4种算法的时间复杂度,我们在CPU为i5-4590,频率3.3 GHz,内存16 GB的计算机系统上用MATLAB编写如下程序来体验长序列卷积和4种计算方法耗时情况(也即时间复杂度):
clear; clc; f=22050; t=1800;
m=f*t; n=1024; L=n+m-1;
x=rand(n,1); y=rand(m,1);
t0=tic; z0=conv(x,y); dt=toc(t0)
% ========= define method ==========
t1=tic; z1=zeros(L,1);
for k=1:L
z1(k)=0;
for p=1:n
if (k+1-m<=p)&&(p<=k)
z1(k)=z1(k)+x(p).*y(k+1-p);
end
dt=toc(t1); error=max(abs(z0-z1));
disp([′time(define)=′ num2str(dt) ′s, error=′ num2str(error)])
% ========= FFT method ==============
t1=tic; x0=zeros(L,1); y0=x0;
x0(1:n)=x; y0(1:m)=y;
X=fft(x0,L); Y=fft(y0,L); Z=X.*Y; z2=ifft(Z,L);
dt=toc(t1); error=max(abs(z2-z0));
disp([′time(FFT)=′ num2str(dt) ′s, error=′ num2str(error)])
% ==========Vector Scale Product==========
t1=tic; xf=x(n:-1:1).′ ; yoo=zeros(L+n-1,1);
yoo(n:L)=y; z3=zeros(L,1);
for k=1:L; z3(k)=xf*yoo(k:k+n-1);
end
dt=toc(t1); error=max(abs(z3-z0));
disp([′time(VSP)= ′ num2str(dt) ′s, error=′ num2str(error)])
其中长度n=1024的随机实数序列模拟低通滤波器的单位脉冲响应序列,长度m=22 050×1800=3.969×107的随机实数序列模拟30 min单声道语音采样序列,卷积结果序列模拟实验数据滤波结果。程序中用到4种卷积和计算方法,分别是:(1)MATLAB内部卷积计算函数conv;(2)卷积定义方法;(3)FFT算法;(4)无数据移动的矢量标积算法。程序运行结果见表1。
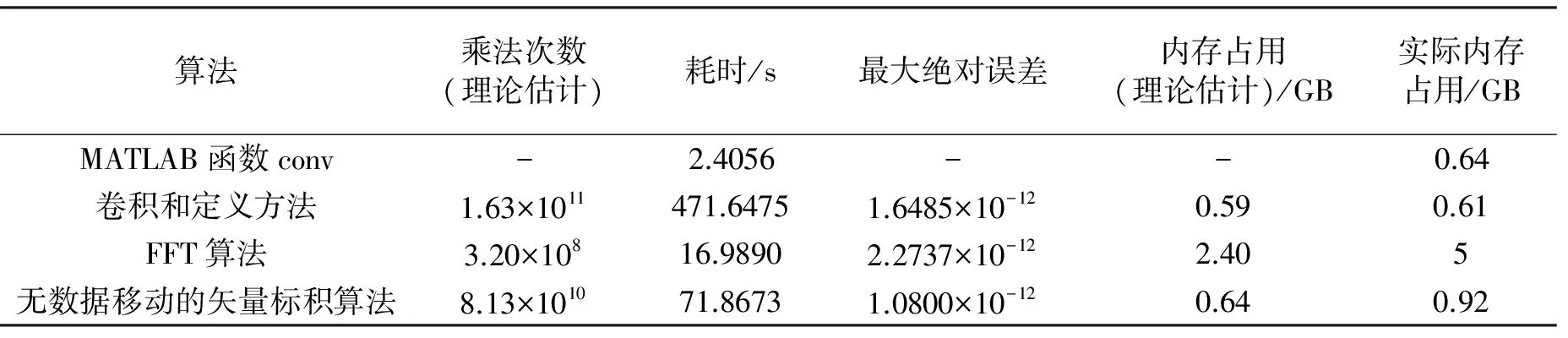
表1 4种卷积和计算方法耗时实验数据表
由于16 GB计算机内存限制和大数据量限制(4千万数据量),矩阵乘法算法未纳入实验。实际内存占用,是用任务管理器读出加载MATLAB(占用内存0.52 GB)后再运行卷积和计算程序时,MATLAB占用内存的峰值减去0.52 GB测算出来的。
表1实验数据与理论估算,数量级是吻合的,实验还表明,FFT算法的计算耗时没有理论预期那么短,内存占用比理论预期还要高。
由表1实验数据表明,我们提出的卷积计算新方法(即无数据移动的矢量标量积算法)确实综合性能优秀,既省空间又省时间,而且算法容易理解。这意味着,对短序列可快速手工计算、对长序列又可以快速编程上机计算,教学和工程应用兼顾。由表1的数据转换成文字,我们得到表2。

表2 3种卷积和计算方法特点比较表
4 结 语
表2的比较,全面地刻画了本文提出的新卷积和计算方法(即无数据移动的矢量标量积算法)的特点。新卷积计算方法,算法本身的特点可以用“反序补零标量积”7个字概括,算法应用及其理论特点也可用“省时省地易实现”7个字来概括。
当然,无数据移动的矢量标量积算法与世界级大师们凝练在MATLAB中的内部conv、Mathematica内部函数ListConvolve中的优秀卷积算法还有巨大的差距。从科学研究层面看,无数据移动的矢量标量积算法仅仅是个初级的中间产物,还需要我们去不断地努力探索。
[1] 吴大正.信号与线性系统分析[M].北京:高等教育出版社,2009.
[2] 高西全,丁玉美.数字信号处理[M].西安:西安电子科技大学出版社,2013.
[3] 杨永生,赵梅.从时域和频域两种角度探讨卷积积分[J].通信技术,2010,43(11):165-168.
[4] 黎明.探讨卷积和的求解方法[J].北京工商大学学报(自然科学版),2005,23(2):49-51.
[5] 陈颖频,程祝媛,王灵芝,等.基于动态坐标和图解法的卷积积分计算[J].闽南师范大学学报(自然科学版),2016(1):29-38.
[6] 李春然.基于Mathematica的卷积计算[J].现代电子技术,2010(19):81-86.
[7] 王益艳.离散序列线性卷积和循环卷积的关系[J].四川文理学院学报,2015,25(5):32-35.
[8] HITZER E.General Steerable Two-sided Clifford Fourier Transform,Convolution and Mustard Convolution[J].Advances in Applied Clifford Algebras,2016,7(9):1-20.
[9] 柳向,王杰贵,方建华.对数据后处理雷达的分段卷积转发干扰研究[J].火力与指挥控制,2016,41(4):15-24.
[10] 刘凤,伍星,潘楠,等.改进时域盲解卷积算法在轴承故障诊断中的应用[J].机械强度,2016,38(2):207-214.
[责任编辑:谢 平]
Method of computing convolution-summation of sequence
JING Min-ying, LONG Shu-ming
(School of Physics and Telecommunication Engineering, Shaanxi University of Technology, Hanzhong 723000, China)
Computing convolution-summation is a method frequently used in discrete linear time-invariant systems response in time domain computed, but computation of convolution-summation is very complicated both in time and in space, especially in computing longer sequences. This paper proposes a new method of computing finite sequence convolution-summation and actualizes the computing method in MATLAB. The result shows that the new method has significantly reduced the computing time and space complexity and achieves greater speed in computing convolution-summation of sequence in small memory computer system.
linear time-invariant systems; series; convolution-summation; vector scalar product; MATLAB procedure
O173
A
2096-3998(2017)05-0081-05
2017-03-10
2017-07-05
井敏英(1978—),女,陕西省富平县人,陕西理工大学讲师,硕士,主要研究方向为信号处理;龙姝明(1955—),男,陕西省城固县人,陕西理工大学教授,主要研究方向为量子物理、计算物理、数据处理。

