基于强化区间线性规划的工程项目模糊多目标均衡优化

蒋红妍，王鑫业，布亚军

（西安建筑科技大学 土木工程学院，西安 710055）

基于强化区间线性规划的工程项目模糊多目标均衡优化

蒋红妍，王鑫业，布亚军

（西安建筑科技大学 土木工程学院，西安 710055）

文章考虑工程项目实施过程中的不确定因素，建立工期、成本、质量模糊均衡优化（FTCQP）模型；运用分解定理、强化区间线性规划（EILP）方法，求出各目标的最优值区间；进一步引入模糊偏好关系，运用模糊折衷规划法，得到FTCQP模型的最优模糊折衷解。最后通过案例分析验证了方法的合理性、有效性和可操作性。

模糊多目标优化；风险水平；强化区间线性规划；模糊折衷规划；模糊偏好关系

0 引言

工程项目的工期-成本-质量均衡优化问题（time-costqualitytrade-offproblem,TCQP）是国内外学者研究的热点。工程项目实施过程中存在诸如场地条件、天气状况、管理水平等不确定因素[1]，使工期、成本、质量目标具有模糊性，因此研究模糊环境下的工程项目工期-成本-质量均衡优化问题（fuzzy time-cost-quality trade-off problem,FTCQP）更符合工程实际情况[2]。

已有研究在建立FTCQP模型的基础上，部分学者运用模糊多属性效用相关理论[3，4]，只给出了一组最优方案；部分学者设计了智能算法得到了Pareto解[5，6]，由于Pareto解分布范围广，使决策者选择最优解仍是一个多目标过程，无法完成全部的决策过程[7]；还有学者运用模糊折衷规划法，得到模型最优折衷解的变化范围[8]，但解空间内存在不可行解。不仅如此，上述研究还存在未考虑决策风险、决策者偏好等实际因素，导致求解结果无法为决策者提供有益信息等问题。本文拟在建立FTCQP模型的基础上，引入决策风险、模糊偏好关系，运用强化区间线性规划(enhanced interval linear programming，EILP)方法，改善FTCQP模型的求解，从而使求解结果能更好的辅助决策者决策。

1 模糊集理论

模糊数是一个连续的模糊集合，具有以下性质：凸状态，即隶属函数有一个明显的峰；正常状态，即保证集合中至少有一个元素隶属度为1。这两个性质决定了模糊数特别适于描述不确定的数值。本文采用三角模糊数来表示项目中的不确定量，如工序持续时间可用N=(l,n,r)表示，其隶属度函数见图1，图中l、n、r三点分别代表工序在最乐观、最可能、最悲观情况下持续时间的取值。

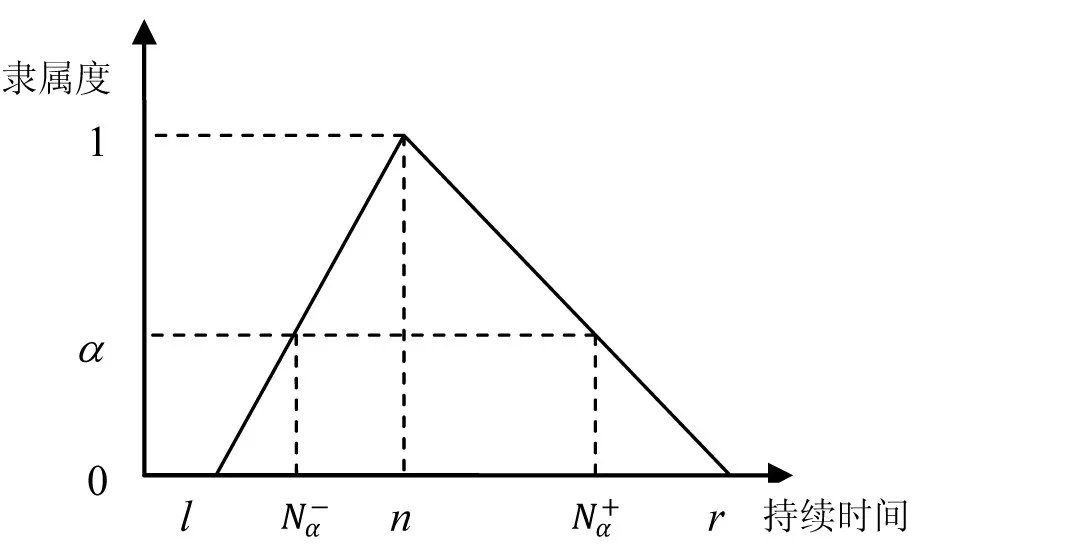
图1 工序持续时间的隶属度函数和α截集

由分解定理知，任意模糊数的α截集为区间数。图1中，三角模糊数N=(l,n,r)，其α截集是实数域上的一个闭区间，可记为，其中α∈[0,1]，称为风险（置信）水平，简称水平；分别为区间的左、右边界。

2 FTCQP模型的建立

2．1 定义与假设

工序施工一般会采用正常模式，也可能采用压缩模式。本文建立的FTCQP模型基于以下定义与假设。

（1）仅当施工持续时间小于正常模式施工持续时间的左边界时，工序才以压缩模式施工[9]。

（2）假定在压缩模式下施工时，工作的直接成本与其持续时间成反比关系；用成本变化率（）表示单位压缩时间对工序直接成本的影响程度，其计算公式见下页式（1）。

（3）由于在实际施工中，很少考虑采用压缩模式对施工间接成本的影响，本文忽略间接成本，用直接成本代替总成本。但本文方法同样适用于考虑间接成本的情况；

（4）假定在压缩模式下施工，工序持续时间与质量成正比关系；用质量变化率（）表示单位压缩时间对工序质量的影响程度，其计算公式见式（2）。

（5）用0～1间的连续数值表示某项工序的质量，越接近1表示工序质量越好；整个工程的质量等于各项工序的质量加权。

2．2 模型建立

基于上述定义和假设，为使工期最短、成本最低、质量水平最高，建立如式（3）所示的FTCQP模型：

式（3）中，i为工序编号；k为工序i所有紧后工序中开始时间最早的工序，i，k=1,2,…,m，m为工序总个数；p为关键路径上的工序集合；为工序i的实际持续时间；为工序i以正常模式施工的持续时间、施工成本、质量；ωi为工序i的质量权重；为工序i的最早开始时间;为工序i以压缩模式施工的持续时间。

3 FTCQP模型的求解

式（3）中，目标函数和约束条件均含模糊数，其求解实质上是一个模糊线性规划问题，应首先对其中的模糊数进行去模糊化处理。为在优化过程中反映出决策风险，本文选用截集法来处理模糊数；将模糊数处理为区间数后，便可运用区间线性规划的相关理论和方法来求解模型。

区间线性规划是指系数含有区间数的线性规划方法，其所需信息量少且求解方便，因此在不确定性优化问题中得到了广泛应用，并已证明效果良好。

本文选用区间线性规划的EILP方法来求解模型，该方法具有计算时间短、效率高、优化过程中能直接反映不确定性、可保证所求非极端解在最终解空间绝对可行等优点[10]。但EILP方法一般用于单目标区间优化问题的求解，且因优化结果为最优值区间，无法得到最优值的确定值。因此，本文将在EILP优化结果的基础上，进一步运用模糊折衷规划来求解多目标问题的最优折衷解。

3．1 FTCQP模型的去模糊化处理

采用截集法对式（3）进行去模糊化处理，并按区间数运算法则整理，得到如下的区间数TCQP模型，见式（4）。

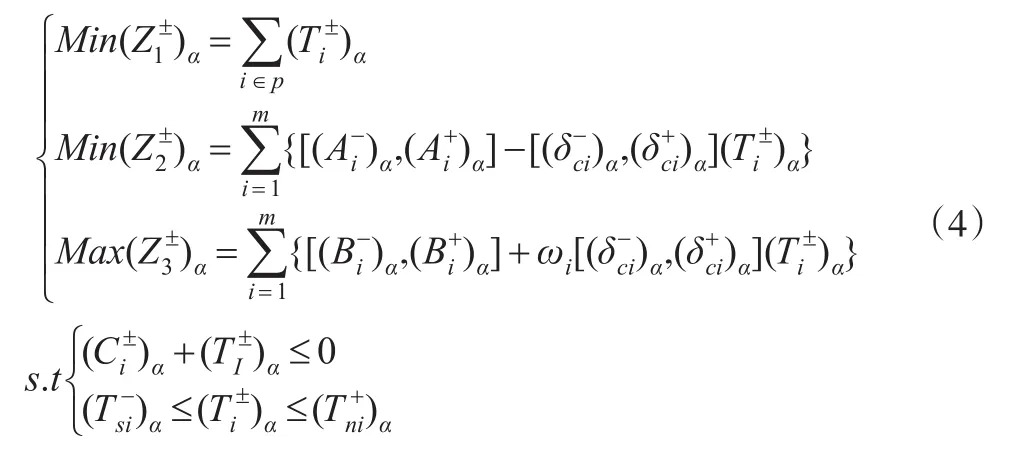
3．2 EILP模型构造及求解

EILP方法求解区间规划的基本思路是：先利用强化区间不确定性定理，对目标函数和约束条件进行处理，将模型分解为上限、下限两个子模型；再求解这两个子模型得到各目标的最优解区间及最优值区间。

为不失普遍性，本文以式（5）所示的区间线性规划模型为例，阐述EILP方法对目标函数和约束条件处理的方法，方法的理论依据及详细证明参见文献[11-12]。

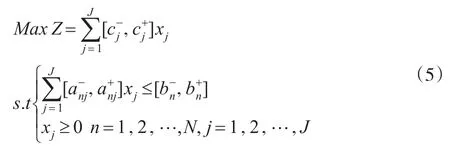
首先应对目标函数进行处理。设式（5）的目标函数中，前t个系数为正其余(J-t)个系数为负为降低EILP模型目标函数的不确定度，引入适宜区间(AI±)替换原来的目标函数,(AI±)定义为：

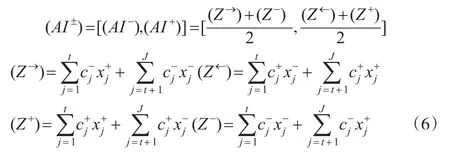
用适宜区间替换式（5）中的目标函数后，原目标函数转换为MaxAI+和MaxAI-两个子目标函数，分别如式（7）、式（8）所示。

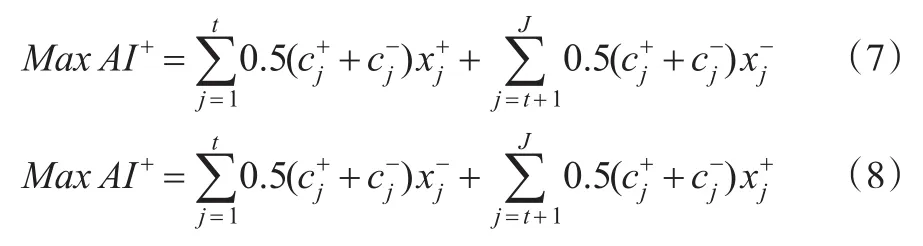
为保证得到最优决策，还应对式（5）的约束条件进行处理。根据EILP方法，求解MaxAI+子目标函数时，约束条件的处理结果为式（9）：

联立式（7）和式（9），可得到式（5）的上限子模型。求解该模型可得到最优解以及最优目标函数

求解MinAI-子目标函数时，约束条件的处理结果为式（10）：

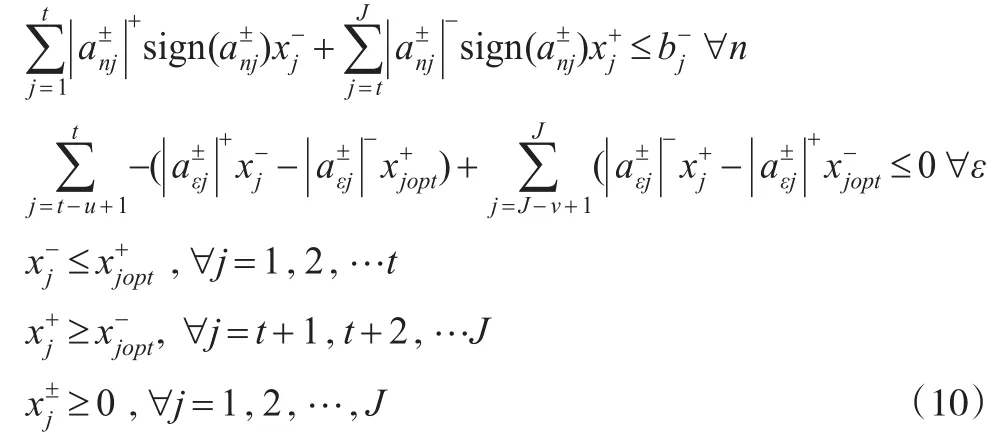
上述约束条件中的第2个约束是为保证EILP的最优解绝对可行，在求解MinAI-时增加的额外约束条件，其中ε为式（9）约束条件中满足：1,…,J)的约束条件的个数。

联立式（8）和式（10）得到式（5）的下限子模型，求解该模型得到以及最优目标函数下限，由此得到式（5）最优解区间和最优函数值区间。

最小化优化问题中目标函数和约束条件处理方法类似，不再赘述。

对于式（4）中的问题，先按照上述EILP方法处理该式的目标函数和约束条件，然后按照成本型目标先求目标函数下限、效益型目标先求目标函数上限的原则，建立式（4）的EILP上限子模型，如式（11）所示：

将各目标函数当作式（11）约束条件下的单目标问题求解，分别得到及及及其中，为水平α下，目标s在约束条件下最优解的左、右边界。

利用上述求解结果，按照成本型目标求目标函数上限，效益型目标求目标函数下限的原则，建立式（4）的EILP下限子模型，如式（12）所示：

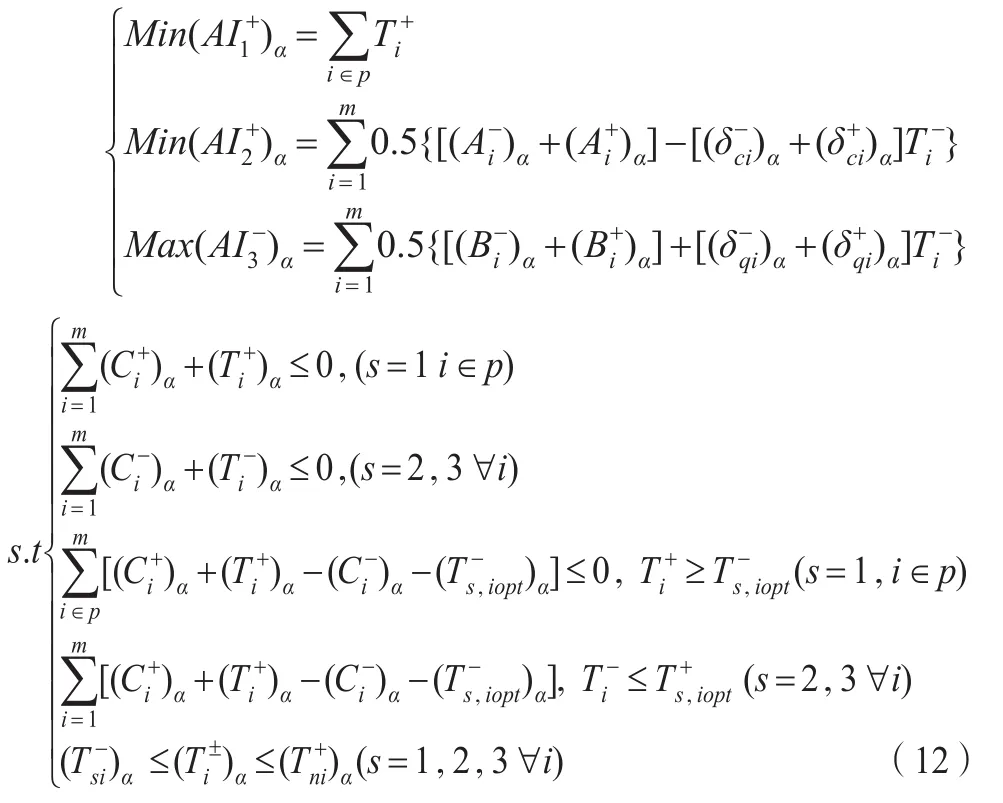
将各目标当作式（12）约束条件下的单目标问题进行求解，分别得到及及及

3．3 FTCQP模型的最优折衷解

由于模型中工期、成本、质量各目标间相互矛盾、彼此制约，几乎不存在使每个目标均达到最优的解，因此需要设法求得其最优折衷解，使所有目标的综合隶属度整体评价值最大。本文采用模糊折衷规划法来寻求多目标问题的最优折衷解，其求解步骤如下。

首先，根据求出的各目标最优值上下边界，利用式（13）、式（14）定义各目标的相对优属度，以量化水平α下，第s个目标的函数值相对该目标最优值的优越程度。

然后，采用最大隶属度偏差法，利用式（15）对多目标进行整体评价[13]。

式（15）中，(Dq)α为水平α下，方案到负理想解的加权Minkowski距离；q为正实数；λs为目标s的权重；φ-为负理想解的目标优属度。对于式（4）中的问题，φ-={0,0,0}。

欲得到折衷解，应使折衷解离负理想解越远越好，即求式（16）。由此，式（3）中的模糊多目标规划问题转化成式（16）的模糊折衷规划问题。

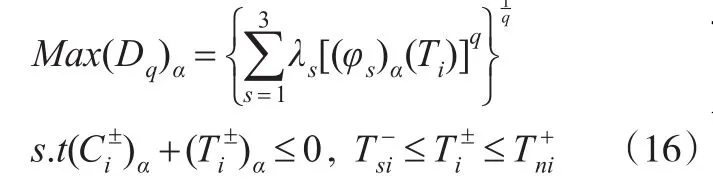
式（16）中各目标的权重值直接影响到优化结果。考虑到决策者对各目标的偏好程度不同，本文采用文献[14]的方法，引入模糊偏好关系来计算各目标函数的权重，使优化结果能更好地反映决策者偏好信息。表1列出了主要的模糊偏好关系。

表1 模糊偏好关系及其含义

通过上述步骤，求得FTCQP模型在水平α下的最优折衷解；当α取遍可行域内所有值时，可求得FTCQP模型的全部最优折衷解。本文FTCQP模型建立和求解的步骤如图2所示。

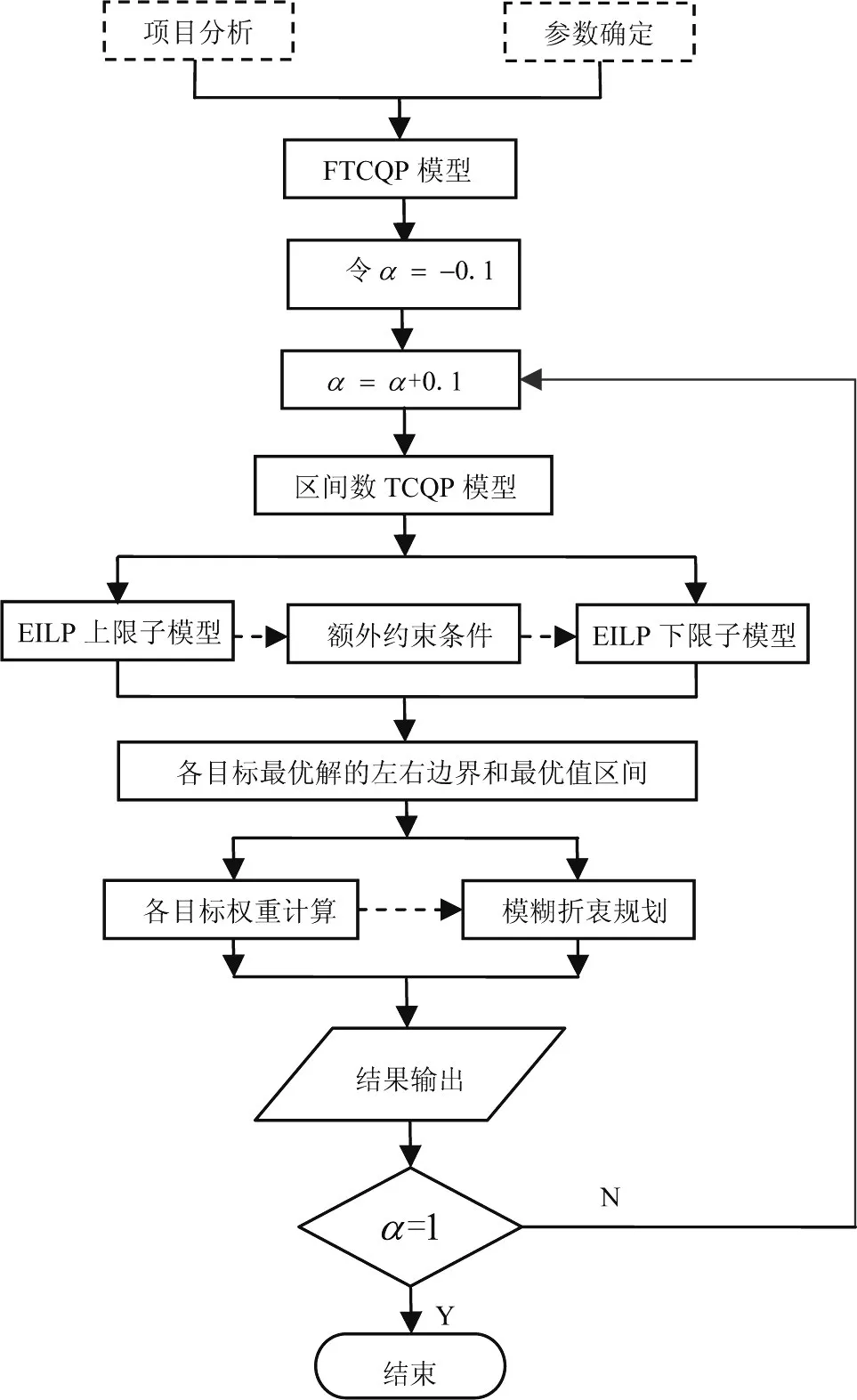
图2 FTCQP模型的建立及求解流程

4 案例分析

结合图3所示的某项目单代号网络图，说明并验证本文提出的方法。该网络图包含7项工序，首尾各有一个虚工序，各工序的基本参数如表2所示。

表2 项目各工序的基本参数

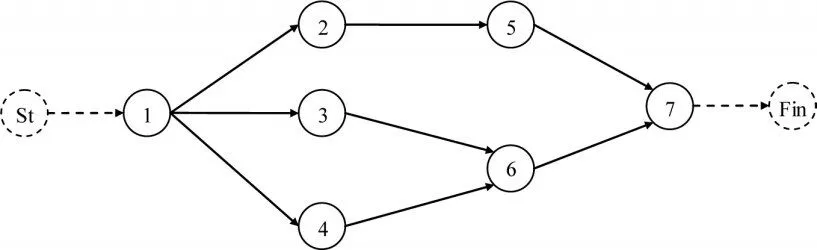
图3 某项目单代号网络图

该项目决策者对各目标的模糊偏好关系为Z2＜＜Z1，Z2＜Z3，Z3＜Z1，利用文献[14]中的方法，求得该项目工期、成本、质量的权重分别为0.43、0.24、0.33。取式（16）中q=1，运用基于MATLAB2012a平台的计算机程序得到该项目在不同水平α下，各目标的最优值区间和最优折衷解，如表3、表4所示。

表3 不同风险水平下各目标的最优值区间

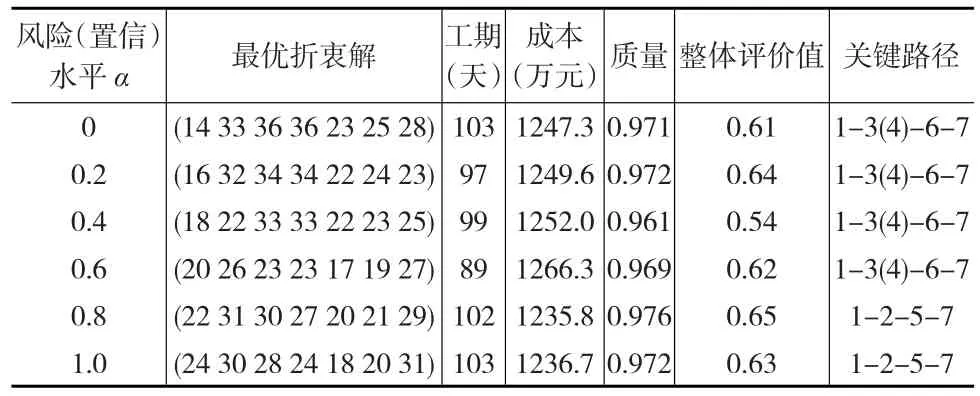
表4 不同风险水平下最优折衷解及相关信息

鉴于篇幅原因，表3中只列出了部分风险水平下各目标最优值的变化范围。当α水平较低时，决策风险较高，各目标最优值的变化范围较大；随着α水平增加，决策风险降低，各目标最优值的变化范围也随之变小。从整体来看，利用本文算法求得的工期、成本最优值区间变动范围较广，质量水平均较高，能从不同角度和风险水平下反映出工程项目各目标的最好、最劣情况。

表4列出了多目标优化问题的部分最优折衷解及其相关信息。决策者可通过比较整体评价值的大小，判断出各风险水平下最优折衷解的优劣；但由于整体评价值大的方案往往风险也较高，所以决策时还应结合表3中的计算结果，考虑不同方案的风险和不确定度，通过权衡整体评价值大小和决策风险择优选择。

由此可见，采用本文提出的方法，不仅能得到多目标优化问题的最优方案，还能为决策者提供风险大小、目标可能的变动范围等更多有益信息，方便决策者科学决策；另外，本文采用枚举所有风险水平的做法，可以考虑优化过程中关键路径的变化情况。相比其他多目标优化方法，本文的计算方法更简捷，求解结果更加符合工程项目的实际需求。

5 结论

本文针对工程项目管理目标的不确定性，建立了以工序实际持续时间为决策变量的FTCQP模型，并创造性地运用EILP方法和模糊折衷规划法对模型进行求解，得到了不同风险水平下各目标最优值的变化范围和多目标问题的最优折衷解。算法中所运用的EILP方法，能显著降低目标函数的不确定度，可为后续决策提供非极端区间范围；风险水平的考虑，使决策者在决策之初就能根据自身风险的接受程度，把握一定风险水平下各目标的变动范围及多目标的整体情况；优化过程中枚举所有风险水平的做法，可展示关键路径随风险水平的变化，弥补了已有研究中对此未有考虑的不足；基于模糊偏好关系的权重确定，能在优化过程中充分体现决策者的偏好信息，可有效辅助实际决策。总体看来，本文提出的方法不仅考虑了决策者对风险的接受程度和其对各目标的偏好程度，还在求解方式上更加灵活、切合实际，可以得到保证解空间绝对可行的最优解变化范围，为决策者提供了有力依据。

[1]Heravi G,Faeghi S.Group Decision Making for Stochastic Optimization of Time,Cost,and Quality in Construction Projects[J].Journal of Computing in Civil Engineering,2012,28(2).

[2]Mokhtari H,Baradaran K R,Salmasnia A.Time-cost Tradeoff Analysis in Project Managemnt:An Ant System Approach[J].Engineering Management,Ieee Transaction on,2011,58(1).

[3]Zhang H,Xing F.Fuzzy-multi-objective Particleswarm Optimization for Time-cost-quality Tradeoff in Construction[J].Automation in Construction,2010,19(8).

[4]杨耀红,汪应洛,王能民.工程项目工期成本质量模糊均衡优化研究[J].系统工程理论与实践,2006,26(7).

[5]张连营,岩岳.工期-成本-质量的模糊均衡优化及其pareto解[J].同济大学学报:自然科学版,2013,41(2).

[6]伊长生,高建炳.基于模糊规划的工程项目工期-成本-质量均衡优化研究[J].工程管理学报,2015,29(1).

[7]张华军,赵金,罗慧.基于个人偏好的多目标优化问题目标权重计算方法[J].控制与决策,2014,29(8).

[8]高云莉,李宏男,王楠楠.不确定条件下工程项目的多目标模糊均衡优化[J].数学的认识与实践,2010,40(11).

[9]杨湘,张连营,张杰.工程项目工期-成本综合模糊优化[J].土木工程学报,2003,36(3).

[10]刘年磊,毛国柱,林赵.基于强化区间线性规划方法的流域环境系统管理优化[J].天津大学学报,2012,45(1).

[11]周丰,郭怀成.不确定非线性系统“模拟-优化"耦合模型研究[M].北京:科学出版社,2010.

[12]Zhou F,Huang G H,Chen G X，et al.Enhanced-interval Linear Programming[J].European Journal of Operation Research,2009,199(2).

[13]李荣均.模糊多准则决策理论与应用[M].北京:科学出版社,2002.

[14]Dragan C,Ian C P.Preferences and Their Application in Evolutionary Multi-objective Optimization[J].IEEE Transactions on Evolutionary Computation,2002,6(1).

Fuzzy Multi-objective Trade-off of Construction Project Based on Enhanced Interval Linear Programming Method

Jiang Hongyan,WangXinye,Bu Yajun

(1.School of Civil Engineering,Xi'an University of Architecture&Technology,Xi'an 710055,china)

In view of the uncertainty during construction process,this paper constructs a fuzzy trade-off model about time,cost and quality(FTCQP).Firstly,the paper works out the optimal value interval by use of the decomposition theorem and enhanced interval linear programming(EILP)method.And then the paper introduces fuzzy preference relation and employs fuzzy compromise programming to obtain the optimal compromise solution of FTCQP model.Finally a case analysis is done to verify the rationality,effectiveness and operability of the proposed method.

fuzzy multi-objective optimization;risk level;enhanced interval linear programming;fuzzy compromise programming;fuzzy preference relation

F224

A

1002-6487（2017）20-0172-05

国家自然科学基金资助项目（51408459）

蒋红妍（1974—），女，陕西富平人，副教授，研究方向：土木工程建造与管理。

王鑫业（1993—），女，四川成都人，硕士研究生，研究方向：工程经济与项目管理。

布亚军（1992—），女，山东阳谷人，硕士研究生，研究方向：工程经济与项目管理。

(责任编辑/易永生)