闭环供应链网络动态系统的模型预测控制算法研究
郭海峰,闫翩翩
(沈阳理工大学 自动化与电气工程学院,沈阳 110159)
闭环供应链网络动态系统的模型预测控制算法研究
郭海峰,闫翩翩
(沈阳理工大学 自动化与电气工程学院,沈阳 110159)
研究了闭环供应链网络动态系统的模型预测控制算法。通过建立系统的预测模型,给出状态估计和预测的计算公式。推导了多阶段最优预测模型的表达式,给出了目标函数和反馈校正方法。推导了基于二次优化的约束优化算法,并通过一个算例给出了这种算法的一般步骤。这种算法的本质是通过滚动优化和滚动实施,不断适时调整订货量、生产量等控制变量,使系统在稳定的前提下得到良好的动态性能,使牛鞭效应得到抑制。这种方法为处理复杂非线性的闭环供应链网络的稳定和协同控制,提供了一种新的方法。
模型预测控制;闭环供应链网络;牛鞭效应
模型预测控制(Model Predictive Control,MPC)是20世纪70年代产生于工业过程控制领域的一类计算机控制算法[1]。不同于其他控制理论,MPC通过滚动优化、滚动实施得到较好的动态控制性能。应用领域也由原来的工业过程控制迅速扩展到航空、航天等许多工业领域。目前MPC在供应链领域的应用研究主要是从约束模型预测控制、鲁棒模型预测控制、非线性模型预测控制以及与其他算法相结合的模型预测控制的角度处理单个供应链若干节点的情况[2-8],而对考虑回收再制造过程的闭环供应链以及闭环供应链网络协同方面的相关报道不多。
本文在相关研究基础上探讨闭环供应链网络动态系统的模型预测控制算法,主要工作有:(1)给出闭环供应链网络动态模型;(2)闭环供应链网络动态系统的模型预测控制算法研究。建立系统的预测模型,给出状态估计和预测的计算公式,推导了多阶段最优预测模型的表达式,给出了目标函数和反馈校正方法,推导了基于二次优化的约束优化算法;(3)给出闭环供应链牛鞭效应的量化方法;(4)通过仿真计算一个包含无缺陷退货和回收再制造的三级闭环供应链网络,给出了该算法一般步骤。仿真结果表明,这种算法对系统的状态变量和控制变量动以及牛鞭效应有很好的控制效果。
1 闭环供应链网络动态模型
研究分析闭环供应链网络动态模型[9],建立如公式(1)所示的系统作为研究对象。
x(k+1)=Ax(k)+Buu(k)+Bdd(k)
z(k)=Cx(k)+Ddd(k)
(1)
式中:向量x(k)表示闭环供应链网络各节点企业在k时刻的库存状态,以及消费者k时刻的虚拟库存,状态变量;向量u(k)分别是各节点企业k时刻的生产完成量或向上游企业的订货量,控制变量;向量d(k)是k时刻的需求,外生变量;向量z(k)是可测量输出;A、Bu、Bd、C、Dd是适当维数的参数矩阵,表示系统的结构。
2 闭环供应链的预测控制方法
2.1 预测模型
将测量向量估计zm描述为如下形式:
zm(k)=z(k)+v(k)
(2)
式中,v(k)代表测量噪声。在供应链里的其他相关变量x(k)和d(k)被当做符合某种可预测的干扰。假设d(k)是一个随机信号,可以通过以下模型描述:
xm(k+1)=Awxw(k)+Bww(k)
(3)
d(k)=Cwxw(k)
(4)
式中,Aw的所有特征值在单位圆内,w(k)是一个加性白噪声。考虑公式(1~4),可以得到系统(1)扩展状态矩阵方程
X(k+1)=ΦX(k)+ΓuΔu(k)+ΓwΔw(k)
Z(k)=ΞX(k)+Ddd(k)+v(k)
(5)
式中:
2.2 状态估计和预测
闭环供应链网络系统的状态、不可测扰动和噪声须使用扩展系统模型(5)来估计。利用卡尔曼滤波器作为最优状态估计器[10],如下式描述。
X(k+1|k=ΦX(k|k)+ΓuΔu(k)
(6)
X(k+1|k+1)=X(k+1|k)+Kf(Zm(k+1)-
ΞX(k+1|k))
(7)
式中Kf是滤波器增益,通常通过代数Riccati方程来求解。由于负载扰动和测量噪声的协方差矩阵不可能准确得到,这里设置滤波器增益为一个基于信噪比的调整参数是更可行的方法。
2.3 多阶段最优模型参考预测算法的推导
由公式(6)推导系统状态在k时刻对k+i时刻的估计为
X(k+i|k)=ΦX(k+i-1|k)+
(8)
进一步将公式(8)描述的系列估计方程写成向量形式
(9)
式中:
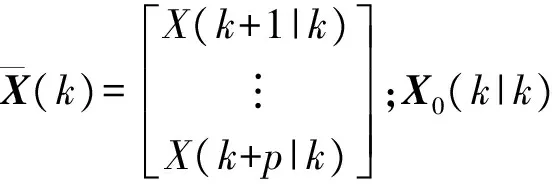
ΔU=[Δu(k|k) … Δu(k+m-1|k)]T;
2.4 目标函数和反馈校正
系统目标函数向量形式如式(10)所示。
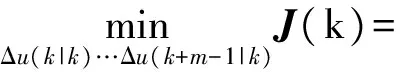

(10)
式中:等号右边第一项表示系统状态与期望值之间的误差;第二项表示控制器校正的变化量;R(k)表示状态期望值;p是预测周期;m是控制时域;Q、R分别称为误差权矩阵和控制权矩阵。
将公式(9)代入公式(10),并通过∂J(k)/∂ΔU(k)=0可得k时刻的目标函数J(k)取最小值时的ΔU(k)。
(11)
则,k时刻控制器的校正量为
(12)

2.5 基于二次优化的约束优化算法
将公式(9)代入公式(10)展开推导,并简化可得
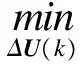
(13)
约束条件:
产能和订货量约束Umin≤U(k)≤Umax;
库存、需求和可测输出的约束Zmin≤Z(k)≤Zmax;生产变化量约束ΔUmin≤ΔU(k)≤ΔUmax。这是一个标准二次优化问题。
3 牛鞭效应的描述
牛鞭效应是供应链末端需求方差向前端传递过程中的增强效应,广泛存在于供应链系统中,不仅是供应链结构中最为重要的性能指标,也是供应链运营中最为重要的绩效指标[9]。为验证这种算法的有效性,选择文献[9]描述的牛鞭效应的方法。

(14)
4 算例
图1为一个由制造商、零售商和消费者组成包含无缺陷退货和回收再制造的三级闭环供应链。
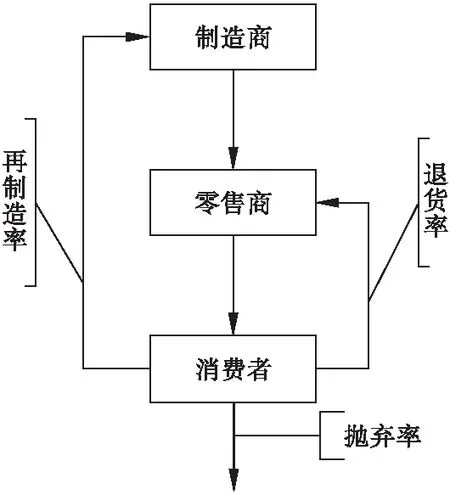
图1 三级闭环供应链
图中:再制造率为λ=0.1,抛弃率为μ=0.2,无缺陷退货率为α=0.1,则λ+μ+α≤1。由文献[3]可知,不需要对系统中的每一个状态的预测,为了简便只考虑关于输出的所有扰动的集中影响,即Dd=0。考虑供应链动态性能,如果假设负荷扰动是加性白噪声以及不存在不同输出之间的相关扰动耦合,可令Aw=I,Bw=I,Cw=I。则系统的参数矩阵为
算法步骤:
(1)初始化。设定初始标称值
x=[5 7 8 6 5 4 6]T,
u=[5 6 0 0 0 0 0]T;初始波动
w0=[0.5 -0.1 0.2 0.1 0 0 0]T,
x0=[0.8 -1 3 -2 0 0 0]T;控制时域p=6,优化时域m=5,计算时长k=30;权系数Q=0.1×eye(P×7),R=0.2×eye(M×3);式中eye函数用于产生单位矩阵;卡尔曼增益系数Kf=diag[0 0 0 0.16 0.2 0.32 0.1]。

(3)考虑生产和订货波动符合约束-0.2≤ΔU(k)≤0.2,求解由公式(13)表示的标准二次优化问题,得到ΔU(k)。
(4)读取向量ΔU(k),取其中的即时控制增量Δu(k|k)构成实际的控制量u(k+1|k)=u(k|k)+Δu(k|k)作用于对象,即所谓反馈校正。
(5)综合考虑公式(2)~(4),由公式(6)、(7)得到k+1时刻新的初始值估计值,又提出类似的优化问题,返回步骤(3)求出Δu(k+1|k+1),既所谓滚动优化。
(6)由计算得到实际数值,根据公式(14)算出牛鞭效应。

图2 库存量波动
图2显示了制造商和零售商库存的波动,图3显示了制造商的生产量、零售商的订货量的波动,它们在预测控制的作用下分别随着时间序列k逐步趋近标称值。图4显示了预测控制方法对系统牛鞭效应的抑制变化曲线。这证明了预测控制算法的有效性。

图3 生产量/订货量波动

图4 牛鞭效应
5 结束语
在相关研究基础上,研究了闭环供应链网络动态系统的模型预测控制算法,并通过一个算例给出了这种算法的一般步骤。这种算法的本质是通过滚动优化和滚动实施,不断适时调整订货量、生产量等控制变量,使系统在稳定的前提下得到良好的动态性能,使牛鞭效应得到抑制。这种方法与供应链管理中已经存在的订货、生产和物流的计划与实施过程非常相似,具有很好的应用前景。这种方法为处理复杂非线性的闭环供应链网络的稳定和协同控制,提供了一种新的方法,并为进一步开发供应链管理软件提供理论支撑。
[1] 席裕庚,庚晓军,陈虹.预测控制性能研究新进展[J].控制理论与应用,2000,17(4):469-485.
[2] M W Braun,D E Rivera,M E Flores,et al.A Model Predicetive Control framework for robust management of multi-product,multi-echelon demand networks[J].Annual Reviews in Control,2003(27):229-245.
[3] Wang W,Rivera D E,Kempf K G.A novel model predictive control algorithm for supply chain management in semiconductor manufacturing [C]//Proc.American Control Conference.California,2005,1:208-213.
[4] William,B Dunbar,S Desa.Distributed Model Predictive Control for Dynamic Supply Chain Management[C]//Workshop on Assessment and Future Directions of NMPC.Freudenstadt-Lauterbad,Germany,2005:26-30.
[5] 董海,王宛,李彦平,等.分布式MPC在网络化制造环境下SCM中的应用[J].系统仿真学报,2007,19(6):1354-1357.
[6] 陈文博,杨春节,曹柬.模型预测控制策略的供应链库存与生产优化调度方法[J].现代制造工程,2009(5):1-5.
[7] Xiang Li,Thomas E Marlin.Robust supply chain performance via Model Predictive Control[J].Computers and Chemical Engineering,2009(33):2134-2143.
[8] Dongfei Fu,Clara Mihaela Ionescu,El-Houssaine Aghezzaf,et al.A Centralized Model Predictive Control Strategy for Dynamic Supply Chain Management[J].IFAC Proceedings Volumes,2013,46(9):1608-1615.
[9] 郭海峰,朱立忠.基于鲁棒控制的闭环供应链网络协同控制方法研究[J].沈阳理工大学学报,2008,27(6):5-8,13.
[10] Lee J,Z H Yu.Tuning of model predictive controllers for robust performance[J].Computers Chem.Engng,1994,18(1):15-37.
(责任编辑:马金发)
StudyonModelPredictiveControlAlgorithmofClosed-loopSupplyChainNetworksDynamicSystem
GUO Haifeng,YAN Pianpian
(Shenyang Ligong University,Shenyang 110159,China)
A model predictive control algorithm of closed-loop supply chain networks dynamic system is studied.Based on the established system prediction model,the calculation formula of state estimation and prediction are given;the multi-stage optimal prediction model expressions are deduced;the objective function and the feedback correction method are given;the constrained optimization algorithm based on quadratic optimization is derived;and the general steps of this algorithm are given by a numerical example.The essence of this algorithm is that through the rolling optimization and continuous implementations,adjusting the order quantity,production control variables,the system has good dynamic performances in the premise of stability,the bullwhip effect is restrained.In order to get the stability and coordination control method of the complex nonlinear closed-loop supply chain networks,a new method is presented.
closed-loop supply chain networks;model predictive control;bullwhip effect
TP273
A
2016-11-07
国家自然科学基金资助项目(70702036)
郭海峰(1970—),男,教授,研究方向:系统工程与供应链管理,先进控制理论与应用。
1003-1251(2017)05-0001-04

