一种基于数据预处理和卡尔曼滤波的 温室监测数据融合算法*

王 振,白星振,马梦白,张致境,高正中

(山东科技大学电气与自动化工程学院,山东 青岛 266590)

项目来源:中国博士后基金项目(2014M551934);山东省中青年科学家奖励基金项目(BS2013DX012);山东省博士后基金项目(201303068)

2016-12-19修改日期2017-06-29

一种基于数据预处理和卡尔曼滤波的 温室监测数据融合算法*

王 振,白星振*,马梦白,张致境,高正中

(山东科技大学电气与自动化工程学院,山东 青岛 266590)

温室具有空间大、无线传感器节点易受到干扰等特点,节点采集的数据波动性较大且易出现丢失现象。为了提高温室监测无线传感网的可靠性和数据融合的精度,提出了一种基于数据预处理和卡尔曼滤波的无线传感器网络数据融合算法。经过对各传感器数据进行预处理和卡尔曼滤波估计,再将数据发送到簇头节点进行基于状态补偿策略的加权数据融合。通过对温室湿度数据进行仿真,结果表明:数据预处理能明显减小数据波动,大幅减少网络数据传输量和能耗,提高抗干扰能力。另外,针对温室无线传感器网络容易出现丢包的现象,基于状态补偿策略的加权数据融合算法可以明显提高在数据丢包情况下的融合精度。

无线传感器网络;数据融合;数据预处理;卡尔曼滤波;状态补偿;湿度

多传感器数据融合能对多个测量数据进行综合分析,能够有效提高其抗干扰能力,能更精确地估测被测参数。无线传感器网络,是一种新型的信息采集及处理技术,以其具有应用成本低、分部规模大和体积小等特点,已应用到温室的环境监测中并发挥着越来越重要的作用[1-3]。温室环境中各种参数分布不均,而且可能会受到各种因素干扰,所以多传感器融合技术对无线传感器网路在温室中的应用起到了至关重要的作用[4-5]。

蔡振江等[6]采用的基于均值的分批估计法,融合精度较高,且只需测量数据无需先验知识,但对传感器分组依赖程度高,分组不当会导致融合差异较大。文献[7]提出了算数平均加权融合,计算速度快,但抗干扰能力差,融合精度较低。Yager[8]提出了一种基于支持度函数的数据融合算法,无需其他概率统计知识,只需当前时刻传感器数据来计算最优融合,并得到了广泛应用[9-10]。熊迎军[11]等人对支持度函数进行了改进,大大减少了算法的运行时间,而且首先对数据进行一致性检测和三次指数平滑,明显减少数据波动,但这种方法运算时占用储存空间大。卡尔曼滤波[12-13]也是目前在数据融合方面应用较多的方法,但是其对状态空间模型的精确性依赖较高,状态空间模型不准确会使融合效果较差。仲崇权[14]刘建书[15]李雪莲等[16]人对最小二乘法在多传感器数据融合方面的应用进行了改进,对传感器方差计算考虑更全面。

针对以上问题,本文提出了基于数据预处理卡尔曼滤波的温室多传感器加权融合算法,算法结构流程如图1所示,首先对测量数据进行基于狄克逊准则的预处理,剔除异常数据提高抗干扰能力,卡尔曼滤波阶段采用状态修正法提高了其在温室环境下应用的精确度,最后采用基于最小二原理的加权数据融合,结合丢包补偿策略提高融合精度。

1 数据融合算法

根据温室传感器的分布特点,本文在使用无线传感器网络监测环境时采取分簇融合的方式,将检测的环境分成多个区域,每个区域有多个传感器节点和一个簇头节点,将区域内测量数据传到簇头节点进行数据融合。本文采用的无线传感器网络数据融合算法主要包括三部分:传感器节点数据预理、局部卡尔曼滤波和基于最小二乘原理的加权数据融合。算法结构如图1所示。

图1 算法结构图

1.1 温室传感器数据预处理

在温室环境下,布置的无线传感器节点数目多,数据采集量大,需要融合的数据量也相应较大。而且受温室环境干扰、传感器精度以及传感器可能会出现的故障的影响,温室无线传感器网络中采集的测量数据可能会出现异常误差较大数据影响融合的可靠性,且这种影响无法忽略。为了剔除误差较大的数据、减少较大环境干扰的影响,本文首先对传感器采集数据进行数据预处理。

本文采取基于狄克逊准则[17]的预处理方法。在处理数据样本量较少时,工程实践中常用的判断数据异常值的方法有格拉布斯准则和狄克逊准则。但是前者适用于剔除一个异常值,且计算量大,特别是需要剔除不止一个异常值时计算更加繁琐,后者则计算过程简单并且可以剔除多个异常值,所以在本文中采用狄克逊准则剔除数据异常值。

表1 样本量不同极差比γ

狄克逊准则剔除异常数据采用的是极差比的方法,设有一组测量数据样本为X1,X2,…,Xn,按照大小顺序排列为X1≤X2≤…≤Xn,根据处理数据个数的不同极差比γ分别如表1所示。

选择不同的显著性水平α,根据处理数据个数n的不同,查表2得相应临界值D(α,n)。若γ>γ′,γ>D(α,n)则判断X1为异常值,剔除X1;若γ<γ′,γ′>D(α,n)则判断Xn为异常值,剔除Xn。

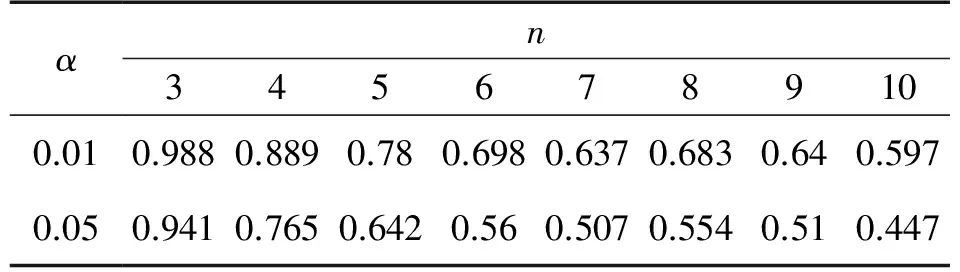
表2 临界值D(α,n)

在数据预处理阶段,首先对测量数据进行分组预处理,处理完一组后再对下组数据进行预处理,然后将处理后数据取均值进行下一步的滤波运算。对传感器节点采集数据的预处理不但可以剔除异常数据,减小数据波动,而且将处理后数据取均值进行后续运算,根据处理数据个数的不同,可以不同程度的减少传感器节点的数据传输量,在无线传感器网络的节点中,无线收发模块会消耗90%以上的能量,因此数据预处理算法也能在很大程度上降低网络能耗,提高网络生命周期。

1.2 局部卡尔曼滤波

尽管已经对温室采集数据进行了预处理,剔除了误差较大数据,但是由于无线传感器本身特性以及在温室环境下无线传感采集数据无法避免的存在着大量测量误差,为了能有效的去除噪声影响,本文采用卡尔曼滤波,更大程度地跟踪温室参数数据真实值。

卡尔曼滤波算法是一种具有较强容错能力,以最小均方误差为准则的递推无偏估计算法,主要是建立滤波过程的状态空间模型,利用前一时刻的系统状态估计值和当前时刻的系统状态观测值并根据系统的过程噪声和观测噪声来更新系统状态变量的估计值,使系统当前的状态估计值能够充分逼近真实值。其滤波主要过程如下:

系统状态方程为:

X(k)=AX(k-1)+W(k)

(1)

式中:X(k),X(k-1)分别为k,k-1时刻的状态值,A为状态转移矩阵,W(k)为过程噪声,W(k)～N(0,Q)。

观测方程为:

Z(k)=HX(k)+V(k)

(2)

式中:Z(k)表示k时刻测量值,H为测量矩阵,V(k)为观测噪声,V(k)～N(0,R)。观测噪声与过程噪声相互独立。

在温室环境下,可以认为过程噪声和观测噪声W(k)、V(k)为高斯白噪声,根据式(1)进行状态一步预测,利用k-1时刻的状态X(k-1|k-1)对k时刻的预测值X(k|k-1)为:

X(k|k-1)=AX(k-1|k-1)+BU(k)

(3)

U(k)为现在状态的控制量,如果没有控制量,可以为0。对应于X(k|k-1)的协方差可以表示为:

P(k|k-1)=AP(k|k)AT+Q

(4)

式中:P(k|k-1)为X(k|k-1)对应的协方差,P(k-1|k-1)为X(k-1|k-1)对应的协方差,AT为A的转置矩阵。

通过式(2)(3)可得到现在k时刻的系统状态最优估计值X(k|k):

X(k|k)=X(k|k-1)+Kg(k)[Z(k)-HX(k|k-1)]

(5)

式中:Kg(k)为卡尔曼增益(Kalman Gain)

Kg(k)=P(k|k-1)HT[HP(k|k-1)HT+R]-1

(6)

为了使卡尔曼滤波算法可以不断运行迭代下去,还需要在每次迭代过程中更新当前k时刻下X(k|k)的协方差:

P(k|k)=[I-Kg(k)H]P(k|k-1)

(7)

式中:I为单位阵。当系统进入下一时刻时,P(k|k)即为式(4)中的P(k-1|k-1),这样卡尔曼滤波根据上述公式就可以不断地自回归迭代下去了。通过迭代公式可以看到,卡尔曼滤波是在时域下的滤波,计算相对简单,在迭代过程中只需储存前一时刻的计算参数,占用储存空间少。

在温室环境存在干扰较多的情况下,数据预处理后进行卡尔曼滤波算法可以有效去除采集数据中系统噪声和传感器测量噪声的影响,跟踪温室被测参数的真实值。

1.3 多传感器融合算法

本文中簇头节点采用基于最小二乘原理的加权数据融合算法。设n个传感器的观测方程为:

Z=Hx+V

(8)

(9)

式中:zi为每个传感器的测量值,wi为其对应的加权系数。定义估计误差:

(10)

式中:测量噪声V为高斯白噪声,期望为0。对式(10)左右两边同时取期望,得:

(11)

由式(11)可知,基于加权最小二乘法的数据融合算法是一种无偏估计算法。根据式(11)求误差的估计方差如式(12),文献[14-15]给出详细证明。

(12)

基于求得的估计误差取最小值的原则,求式(12)对wi的偏导,令其等于零可得:

(13)

可以看到加权系数和测量方差有关。由于本文传感器节点采用了卡尔曼滤波跟踪状态真实值,所以进行加权融合时,本文采用方差估计学习算法,算法流程如下:

设簇头节点有n个数据需要进行数据融合,xi(k)为第i个传感器k时刻的数据。

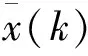
(14)

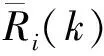
(15)

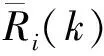
但是在温室环境中,传感器节点向簇头节点传输信息时,可能会出现丢包现象,数据丢包将导致数据融合精度下降,并且当同一节点连续出现丢包或者同一时刻簇内多个节点出现数据丢包现象时,将严重影响传感器工作可靠性,并使簇头节点融合数据不能完全反映温室环境,使网络性能变差。

当某个传感器节点向簇头节点传输数据出现丢包时,有些文章采用使用传感器历史数据,代替丢包数据的方法,但当发生连续丢包问题时,算法性能就会变得很差。本文采用状态补偿策略,通过数据的变化趋势和变化速率进行数据状态预测,将状态预测值作为当前时刻丢包节点的上传数据。

假设,某个传感器节点k有数据上传,k+1时刻出现丢包现象,具体算法流程如下:

δ(k)=x(k)-x(k-1)

(16)

式中:x(k-1)为k-1时刻传感器上传数据,x(k)为k时刻传感器上传数据,δ(k)为在k时刻数据增量,反应测量数据变化速率。当k+1时刻出现丢包现象时,通过式(17)预测作为k+1时刻的状态补偿。

x(k+1)=x(k)+αδ(k)+β(δ(k)-δ(k-1))

(17)

式中:α为速率变化系数,β为趋势变化系数。

对数据丢包采取状态补偿措施,可以有效减低丢包影响,提高融合精度,使无线传感器网络在温室环境监测中应用更加可靠。

2 仿真验证

本文采用温室采集的土壤湿度数据进行数据融合来验证算法有效性,传感器采集数据的间隔为2 min。

图2为一个传感器24 h土壤湿度的变化曲线,可以看到一些采集数据受到干扰较大,曲线有较多明显差异较大的数据,出现异常的波动。

图3为经过数据预处理的土壤湿度变化曲线,数据处理个数为5,可以算出节点数据传输量大约减少80%左右,大大降低了网络能耗,同时根据图2和图3的比较可以看出经过预处理剔除了异常数据的湿度曲线更加平滑,数据波动性小,增强了网络在运行过程中的抗干扰能力。

图2 土壤湿度变化曲线

图3 数据预处理土壤湿度变化曲线

在簇头节点数据融合时,本文采用状态补偿措施来解决传感器节点传输数据出现的数据丢包问题,降低丢包影响,提高融合精度。

图4为数据在丢包率为20%和不丢包两种情况下的土壤湿度融合曲线,可以看到当传感器节点传输数据出现数据丢包问题时,数据融合结果会出现较大误差。

丢包率20%和状态补偿下的数据融合值与不丢包情况下数据融合值的误差如图5所示。从图5可以明显看出在丢包情况下通过状态补偿策略能够大大减少丢包影响,提高融合精度。

图4 数据丢包和不丢包情况土壤湿度曲线

图5 丢包及丢包补偿融合误差

图7 连续丢包情况融合误差

将本文提到的算法与1.3节提到历史数据替代丢包数据的方法进行比较,采用融合数据与不丢包融合数据之间的误差作为评价性能指标,对丢包率20%和连续丢包两种情况进行仿真验证,结果如图6和图7所示。从图中可以看到本文提出的方法要优于历史数据替代法,特别是在出现连续丢包的情况下,本文提出的方法的数据融合精度要高很多。

图6 丢包率20%情况融合误差

3 结论

针对无线传感器网络在温室环境下的多传感器融合,会出现干扰导致的数据波动问题,并且传感器传输数据过程可能出现丢包现象等问题,本文提出了基于数据预处理的卡尔曼滤波,并对多传感器数据进行基于最小二乘原理的加权融合。通过理论分析及温室湿度测量数据进行的仿真验证,结果表明本文提出的方法具有良好抗干扰能力,同时能大幅减少数据传输量,减低网络能耗;而且在传感器传输数据丢包的情况下依然能达到较高的融合精度,效果良好。

[1] Jiang H,Hallstrom J O. Fast,Accurate Event Classification on Resource-Lean Embedded Sensors[J]. ACM Transactions on Autonomous and Adaptive Systems,2013,8(2):65-80.

[2] 刁智华,陈立平,吴刚,等. 设施环境无线监控系统的设计与实现[J]. 农业工程学报,2008,24(7):146-150.

[3] 李莉,李海霞,刘卉. 基于无线传感器网络的温室环境监测系统[J]. 农业机械学报,2009,40(S1):228-231.

[4] Huang L,Xiao J. Application Research of Intelligent Greenhouse’s Control System Based on Multi-Sensor Data Fusion[C]//Second International Conference on Computer Modeling and Simulation,2010. ICCMS’10. IEEE,2010,4:211-214.

[5] Yinghui L,Genqing D. Study on Data Fusion of Wireless Monitoring System for Greenhouse[C]//2015 8th International Conference on Intelligent Computation Technology and Automation(ICICTA). IEEE,2015:864-866.

[6] 蔡振江,康健一,张青,等. 数据融合技术在温室温度检测中的应用[J]. 农业机械学报,2006,37(10):101-103.

[7] Liao Y H,Chou J C. Weighted Data Fusion Use for Ruthenium Dioxide Thin Film pH Array Electrodes[J]. IEEE Sensors Journal,2009,9(7):842-848.

[8] Yager R R. The Power Average Operator[J]. IEEE Transactions on Systems,Man,and Cybernetics—Part A:Systems and Humans,2001,31(6):724-731.

[9] Wang X H,Xu L H,Wei R H. A New Fusion Structure Model on Greenhouse Environment Data and a New Fusion Algorithm of Sunlight[C]//2014 International Conference on Wireless Communication and Sensor Network(WCSN). IEEE,2014:418-424.

[10] 孙田川,刘洁瑜. 基于支持度和自适应加权的MEMS陀螺信息融合算法[J]. 传感技术学报,2016,29(10):1548-1552.

[11] 熊迎军,沈明霞,陆明洲,等. 温室无线传感器网络系统实时数据融合算法[J]. 农业工程学报,2012,28(23):160-166.

[12] Kalman R E. A New Approach to Linear Filtering and Prediction Problems[J]. Journal of Basic Engineering,1960,82(1):35-45.

[13] 金长江,张兵,曹祥杰. 基于容积卡尔曼滤波的异类多传感器一致性融合算法[J]. 传感技术学报,2016,29(7):1006-1010.

[14] 仲崇权,张立勇,杨素英,等. 基于最小二乘原理的多传感器加权融合算法[J]. 仪器仪表学报,2003,24(4):427-430.

[15] 刘建书,李人厚,常宏. 基于相关性函数和最小二乘的多传感器数据融合[J]. 控制与决策,2006,21(6):714-716.

[16] 李雪莲,孙尧,莫宏伟. 基于最小二乘法的冗余信息数据融合算法实现[J]. 计算机工程与应用,2009,45(15):34-38.

[17] Gu J,Fan D,Jiang N,et al. A Noise Detection Method for NDVI Time Series Data Based on Dixon test[C]//2012 First International Conference on Agro-Geoinformatics. IEEE,2012:1-5.

ADataFusionAlgorithmonDataPreprocessingandKalmanFilterforGreenhouseEnvironmentMonitor*

WANGZhen,BAIXingzhen*,MAMengbai,ZHANGZhijing,GAOZhengzhong

(College of Electrical Engineering and Automation,Shandong University of Science and Technology,Qingdao Shandong 266590,China)

The greenhouse has the larger space,and the wireless nodes are vulnerable to the interference from the environment. The data collected by nodes are more volatile and many interference factors easily lead to packet loss. In order to enhance the reliability of wireless sensor neworks for the greenhouse monitoring,and improve the precision of data fusion,a data fusion algorithm on data preprocessing and Kalman filter is proposed. Firstly,the data preprocessing method and Kalman filter is utilized to decrease the influence of abnormal data,then these data are sent to the cluster head and fused on the weighted data fusion algorithm with the state compensation strategy. The simulation is conducted on the greenhouse humidity,which shows that data preprocessing can significantly reduce data fluctuations,the amount of data transmission and the network energy consumption while improve the anti-interference ability of wirless networks. In addition,the weighted data fusion algorithm based on state compensation strategy can also significantly improve the fusion accuracy in the case of packet loss.

wireless sensor network;data fusion;data preprocessing;Kalman filter;state compensation;humidity

TP393

A

1004-1699(2017)10-1525-06

10.3969/j.issn.1004-1699.2017.10.012

王振(1991-),男,山东枣庄人,山东科技大学电气与自动化工程学院硕士研究生,研究方向为无线传感器网络及应用,wzz4585@163.com;

白星振(1977-),男,山东潍坊人,博士,山东科技大学电气与自动化工程学院副教授,研究方向为无线传感器网络,数据融合,滤波估计,xzbai@sdust.edu.cn。