基于Python技术的自然图像随机数生成设计
张明浩 王虹宇 张毅宁
(鞍山师范学院物理科学与技术学院,辽宁 鞍山 114007)
基于Python技术的自然图像随机数生成设计
张明浩 王虹宇 张毅宁
(鞍山师范学院物理科学与技术学院,辽宁 鞍山 114007)
根据随机数验证图形散乱无序这一特征,反演随机数列。大自然中有许多景象,我们从中随机提取一幅或多幅图像。利用Python语言,通过高斯模糊将黑白图像的黑白点均匀化,利用斐波那契数列多次提取等方法,得到一组或多组随机数,最后经过蒙特卡洛π验证,证明这组数是随机数。
斐波那契数列;蒙特卡洛验证;高斯模糊;随机数;Python
1 有关随机数的基本问题
1.1 随机数表需要的理由
目前,数学对随机数(或随机序列)仍然没有统一定义。真随机数性质的一般描述是在随机序列无限长的情况下具有如下性质:
(1)均匀分布:一串真随机序列满足均匀分布的统计特性,如序列的每一位是0或1的概率相等,都为0.5。
(2)不可预测性:真随机序列的每一位是相互独立的,给定序列某一位的值,并不能预测或计算出后一位的值。
基于数学算法的伪随机数发生器实际上可以产生近似于均匀分布随机序列。现代计算机算法已经可以产生足够好的伪随机数,其周期性已经不再是关键问题,但是与真随机数相比最大的区别在于可否对下次结果进行预测。很明显伪随机数虽然快捷,但是对于同样的种子,产生的随机序列将会是相同的,显然不具有不可预测性[1]。
1.2 常见随机数生成方法
常用的产生伪随机数的数学算法有线性同余发生器(linear congruential generator),延迟斐波那契发生器(lagged Fibonacci generator)和线性反馈移位寄存器(linear feedback shift register)等[2]。
除了基于确定数学算法的伪随机数发生器,还有一类是物理伪随机数发生器,产生的随机数是来源于客观的物理过程,但客观的物理过程并不意味着真随机。相对于数学算法,物理伪随机数发生器的随机性两大特点:
一是理论上准确地描述很多实际的物理过程非常困难和复杂,即便是掌握了物理系统的初值和运行规律,也很难精确地计算出这些物理过程将来的状态。
二是周围环境对于物理系统的运行产生影响,比如两个相同的器件由于温度或电压等条件的影响,系统开始运行的初值可能不同,这也导致了预测的困难。
由于本质上很多物理过程并不是真随机的,理论上并不满足不可预测性的要求。所以产生的随机数为伪随机数。其研究设计过程一般是先选取一个物理世界的真随机源,然后选用特定的方法从中提取真随机数。物理真随机数发生器具有真正的随机性和不可预知性,其采样的真实物理现象有多种[3],如:放射性衰变,电子电路噪声,大气噪声,电子振荡器的频率抖动,激光混沌,光子相位噪声,光量子的偏振等。
1.3 常用随机数基本检验方法
常用的基本检验方法有:频数检验,序列检验,扑克检验,游程检验和自相关检验等,但目前并不存在真正意义上的真随机性的检测方法,这是因为真随机性是基于无限长序列的,所以数学统计上的检测是无法完成的。目前工业上常用的统计检测一般是基于固定长度随机序列的(一般是1 Gbit),如 ENT(pseudo-random number sequence test program),NIST-STS(a statistical test suite for the validation of random number generators and pseudo random number generators for cryptographic applications),Diehard(a battery of tests of randomness)等[4]。其中ENT检验为国际上通用的随机数检测程序,将给出产生的随机序列的数学平均值,每比特熵值,χ检测值,Monte Carlo方法计算得到的π值,以及序列相关系数。
2 基于Python技术的自然图像随机数生成的过程
2.1 设计思路及原理说明
首先,从自然界中提取一幅或多幅图像,可以假定一般情况下,这一图像不具有规律重复特征,然后将其转化为黑白图像;转化过程中,利用高斯模糊将黑白图像中的黑白点均匀化,进而转化成0-1序列;再将其转化为一个大十进制数,其后再从这个十进制中按斐波那契序列提取一定数量的数列作为一个十进制数。依次改变提取起始位,经过循环多次提取,获得一组随机数。
2.2 选择Python相关技术的原因
Python是一种面向对象、支持动态语义、内置高级数据结构、语法简洁优美、易于扩展的解释型脚本语言(script language)[5]。OpenCV(Open Source Computer Vision Library)是一个基于(开源)发行的跨平台计算机视觉库,可以运行在Linux、Windows和Mac OS操作系统上。它具有轻量级且高效的特点——由一系列C函数和少量C++类构成,同时提供了Python、Ruby、MATLAB等语言的接口,提供图像处理和计算机视觉方面的很多通用算法1[6]。因此,我们将二者结合进行图像处理。
2.3 图像的二值处理
利用OpenCV工具包对图像进行二值处理十分方便,图像处理前后如图1所示,其过程如下:
im_gray=cv2.cvtColor(image,cv2.COLOR_BGR2GRAY)#用灰度模式打开要处理的图像
retval,im_at_fixed=cv2.threshold(im_gray,50,255,cv2.THRESH_BINARY)#将50-255之间的灰度值作为图像转换的阈值
im_at_gaussian=cv2.adaptiveThreshold(im_gray,255,cv2.ADAPTIVE_THRESH_GAUSSIAN_C,cv2.THRESH_BINARY,5,7)#对图像进行高斯模糊,保证0、1值均匀分布

图1 像处理前后原图与灰度图
2.4 图像的数值转化
进一步将黑白图像转化成0-1序列,存储到文件“num.txt”中。
num=""
for i in range(img.shape[0]):#对图像值的二维数组进行遍历
for j in range(img.shape[1]):
if img[i][j]>100:num+="1"#将高于100灰度值定为1,否则为0
else:num+="0"
f=file("num.txt","a")#将10序列转化为字符型存储到“num.txt”文件中
f.write(str(int(num,2)))
2.5 随机数生成
f=open("num.txt")#打开“num.txt”文件
mystr=f.read()#将“num.txt”文件中的0-1序列读出
f.close()
n=len(mystr)-index[-1]#得到10序列长度
index=[1,2,3,5,8,13,21,33,54,87]#斐波那契数列
num=[0]*n
for i in range(n):
mynum=""
for j in range(len(index)):
mynum+=mystr[i+index[j]]#以斐波那契数列为下标获得一个数组成的字符
num[i]=float(int(mynum)/10000000000.00)#将下标获得的字符变成浮点小数,经循环后变成数组
fo=open("newnum.csv","w");fo.write("random, ")#将浮点小数数组变成字符存储到"newnum.csv"文件中
for i in range(n):fo.write(str(num[i])+","+" ");fo.close()
3 蒙特卡洛π验证
蒙特卡罗方法是以概率和统计理论方法为基础的计算方法[7]。认为平面系上的一个边长为1的正方形及其内部的一个形状不规则的“图形”,向该正方形“随机地”投掷N个点,有M个点落于“图形”内,则该“图形”的面积近似为M/N。而这个图形接近圆,其面积为π。实现代码如下:
import pylab as plt#加载pylab绘图包
incount=0;count=100000;x=[];y=[];
for i in range(count):x.append(num[i]);y.append(num[count+i])#将小数数组赋给蒙特卡洛点变量x,y
if(x[i]**2+y[i]**2)<1:incount+=1#如果x,y对应的点在单位元内,计数加1
plt.scatter(x,y,s=0.1,edgecolors='none')#汇出点图
plt.text(-0,-0.05,"pi="+str(4.0*incount/count))#标记蒙特卡洛比值,并和π做比较
plt.text(-0,-0.10,"count="+str(count));plt.show()
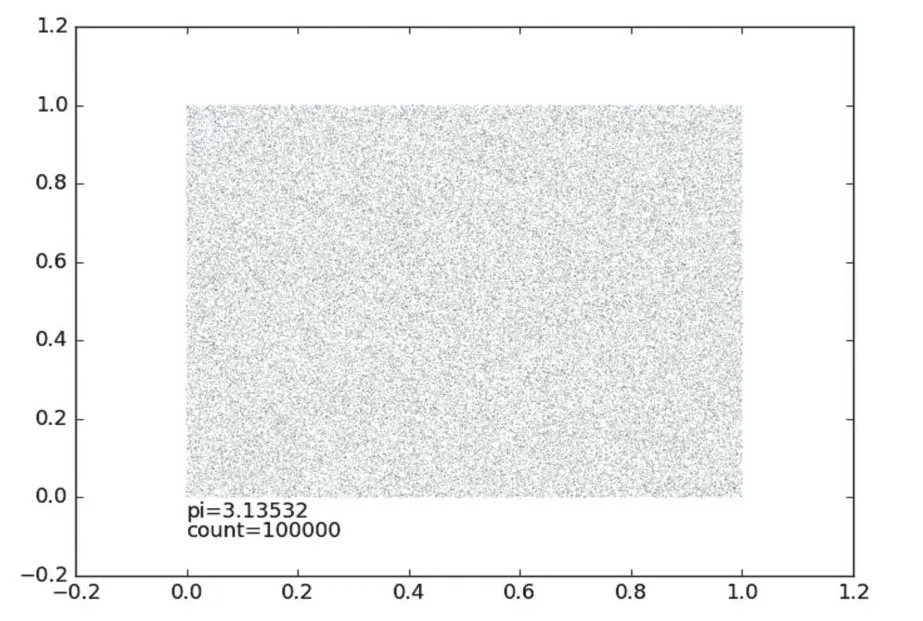
图2 蒙特卡洛π验证图
4 多次实验结果π值统计
我们进行简单随机抽样100次,实验结果π值如下:

图3 实验结果π值统计图
在上述100个数据中,最小值为3.12704,最大值为3.15249,平均值为3.14076,标准误为0.00557。在图3中,横坐标的值为实验数据的数值,纵坐标的值为统计数量。根据图3我们可以得出:左侧的直方图显示,这些数据围绕π这一数值紧密聚类,大体上呈现正态分布,处于稳定状态。中间的概率密度图显示,这些数据的范围无限接近于π值,并且越接近π值,概率越高。右侧的累计曲线显示,在π值附近分布的比重最大。根据上述结果,我们可以看出,实际数值是与理论数值π值非常接近的,也就代表着我们这个实验的准确性。
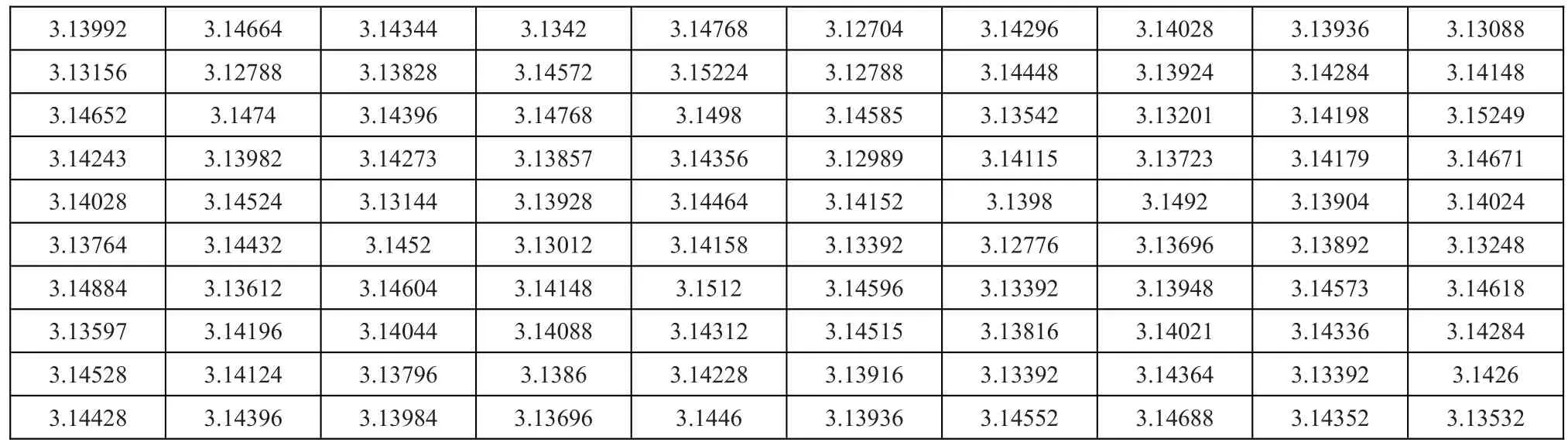
表1 实验结果π值
5 自然图像随机数生成特点
自然图像随机数生成器的设计有其他实验不可比拟的优势:首先,取材方便,一幅自然图片就可以,甚至可以是一个人脸照片;其次,生成速度快,利用计算机程序直接操作处理,没有模数转换过程,不受外界变量控制;再则,成本低,几乎没有实验器材,得到的是优于数学算法的随机数。最为重要的是个性化特点明显,调整不同的照片,就可以提取不同的序列号,确保唯一性。
[1]Aj's Blog.科普:什么是随机数[EB/OL].https://www.6zou.net/docs/what_is_random.html.2016-6-10.
[2]郭弘,刘钰,党安红,等.物理真随机数发生器[J].科学通报,2009(23):3651-3657.
[3]于全福.基于量子效应的随机数产生研究[D].北京:北京大学,2013.
[4]知乎.如何评价一个伪随机数生成算法的优劣[EB/OL].https://www.zhihu.com/question/20222653.2016-6-10.
[5]钟志强.基于Python语言的大学物理实验数据处理方法研究[J].鞍山师范学院学报,2016,18(2):77-81.
[6]李国军.数字图像处理的一种新方法[J].鞍山师范学院学报,2016,18(2):69-73.
[7]百度百科.蒙特卡洛[EB/OL].http://baike.baidu.com.2015-6-10.
Design of Random Number Generation of Natural Image Based on Python
Zhang Minghao Wang Hongyu Zhang Yining
(Anshan Normal University,Anshan 114007,Liaoning)
Random number has the characteristics of disorder and scatter.Based on this,the random series is retrieved.We can randomly extract images from the nature.This paper uses Gauss fuzzy to homogenize the black points and white points in the binary images with Python language,and uses the Fibonacci sequence for extraction to obtain groups of random numbers.Finally,the Monte Carlo test shows that the number is random.
Fibonacci sequence;Monte Carlo method;Gauss blur;random number;Python
TN918.1 文献识别码:A
1008-6609(2017)08-0013-03
张明浩(1996-),男,天津人,本科,研究方向为电子信息科学与技术。
2016年辽宁省大学生创新与创业项目,机械随机数生成器的设计与实验与真随机数表的生成;编号:201610169025。

