基于线性平行粘结接触模型的岩石细观参数选取方法研究

刘良军，曹 智，王俊杰

(1.重庆腾云工程咨询有限公司， 重庆 400020； 2.湖南省水利水电勘测设计研究总院， 湖南 长沙 410007；3.重庆交通大学 国家内河航道整治工程技术研究中心， 重庆 400074；4.重庆交通大学 水利水运工程教育部重点实验室， 重庆 400074)

基于线性平行粘结接触模型的岩石细观参数选取方法研究

刘良军1，曹 智2，王俊杰3,4

(1.重庆腾云工程咨询有限公司， 重庆 400020； 2.湖南省水利水电勘测设计研究总院， 湖南 长沙 410007；3.重庆交通大学 国家内河航道整治工程技术研究中心， 重庆 400074；4.重庆交通大学 水利水运工程教育部重点实验室， 重庆 400074)

基于研究线性平行粘结接触模型中的细观参数与单轴压缩试验应力-应变曲线及试样破坏形式的对应关系，将细观参数分为四类。Ⅰ类，对峰值应力及其应变量敏感，但对初始弹性模量不敏感；Ⅱ类，对应力峰值和初始弹性模量E0均敏感；Ⅲ类，对试样应力-应变曲线的各特征值均不敏感；IV类，对试样破坏形式敏感。利用上述分类结论，制定了岩石细观参数的选取方法：拟合初始弹性模量E0；拟合应力峰值及其对应的应变量；调整破坏模式；结果微调。

岩石；细观参数；线性平行粘结接触模型；数值模拟

近年来，基于离散单元法求解非连续介质力学问题成为岩土类材料特性数值分析的一个热点研究方向。研究人员对此开展了不少有意义的探索，在岩石断裂与损伤[1-3]、边坡稳定及滑坡机理分析[4-5]、围岩稳定性[6]、桩土复合地基承载机理[7]等方面都取得了丰富的研究成果。

然而，如何科学地确定与材料宏观特性相匹配的细观参数成为研究人员开展可靠的数值模拟的重要前提。因此，国内外的学者们开展了大量的土石材料的细观参数及其宏观特性之间定性或定量的关系研究。在岩石材料的研究方面，Huang H Y[8]基于PFC2D内置黏性接触模型(contact bond model)对岩石单轴压缩试验进行了研究，认为单轴压缩强度特性基本不受承压面的宽度与颗粒半径之比的影响。Nardin A等[9]定性地研究了黏性材料细观参数及其宏观特性之间的关系。Hsieh Y M等[10]研究了砂岩的细观组分含量、变形机制以及砂岩宏观力学特性之间的关系。徐金明等[11]构建了含裂隙的石灰岩离散元模型，并解释了相关细观参数的含义。丛宇等[12]结合大理岩室内试验数据，定量地分析了大理岩的宏细观参数间的关系。赵国彦[13]等基于线性平行粘结接触模型(linear parallel bond contact model)研究了颗粒单元半径比、刚度比等参数对宏观变形特性的影响。相比于岩石材料，非黏性土料方面的宏细观研究略为丰富，并以周健等[14]、尹成薇等[15]、徐小敏等[16]以砂土类材料为研究对象的分析居多。

目前针对岩石类材料的细观参数选取方法缺少系统性研究，大部分研究成果为基于砂土类材料特性的基础之上得出，并未给出细观参数选取方法或步骤，多为定性分析。本文基于线性平行粘结接触模型(the linear parallel bond contact model)，对岩石细观参数机器宏观特性之间的关系开展了大量模拟工作，以不同细观参数对应力-应变曲线特征及试样断裂形式的影响效果为基础，归纳岩石类材料的基本单元的选取方法和细观参数的选取方法，力求为岩石类材料细观参数的研究提供一些有价值的认识和讨论。

1 试验方案及结果分析

1.1 模型构建

岩石试样在受到外力作用后可能会发生破碎，假定当碎屑粒径小于一定值后，该颗粒将不再发生破碎。利用“等质量逐级替换最细颗粒”方法对试验室用砂岩料的级配曲线进行修正[17]，综合考虑工作站的运行效率，取修正后的砂岩料级配中的最小粒组1.0 mm～2.0 mm作为基本颗粒单元。

如图1所示，本文构建的岩石单轴压缩试验模拟系统主要包括以下几个部分： 岩石离散元试样(50 mm×100 mm)，加载模块，数据采集模块。试样模型中的基本颗粒单元通过线性平行粘结接触属性连接。本岩石试样共生成8 268个接触，且每个接触的线性平行粘结模型属性均被激活。

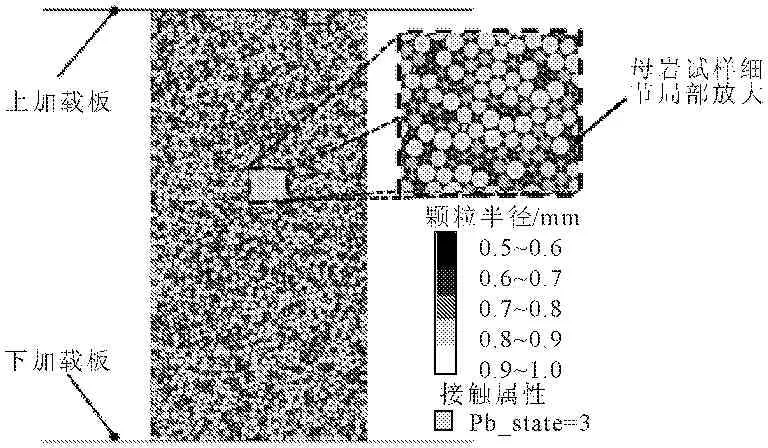
图1岩石试样单轴试验模型示意图

1.2 试验方案

岩石试样单轴试验数值模拟方案见表1。

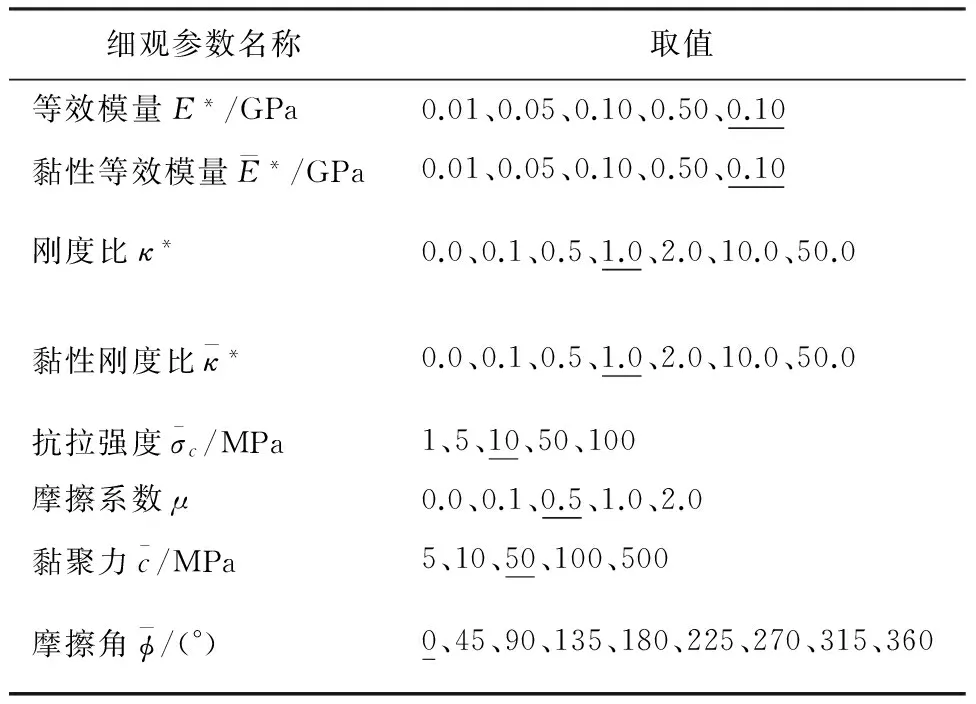
表1 接触属性取值表

注：表中数值加粗并带下划线的数值为基准值。

采用单一变量法逐一对线性平行粘结模型中的各细观参数进行敏感性分析。虽然不同细观参数的取值区间有所差别，但是均设定了一个基准值试验参数，以便进行平行比较。

1.3 敏感性分析

将各个细观参数的取值进行归一化处理，从而转换化为无量纲的值，分析细观参数对应力-应变曲线特征量的敏感性，见图2～图4。

图2 细观参数对初始弹性模量的影响

图3 细观参数对峰值应力的影响

图4细观参数对峰值应力对应的应变量的影响

由图2、图3、图4可知，随着线性平行粘结接触模型中各细观参数取值的增大，对应力-应变曲线特征量的影响趋势可分为四类：① 产生正效应的系列曲线；② 产生负效应的系列曲线；③ 产生周期性效应的系列曲线；④ 几乎无影响的系列曲线。结合细观参数对颗粒间接触破坏的影响，将线性平行粘结模型中的细观参数按对不同宏观特性的敏感性程度分为以下四类：

Ⅰ类：对峰值应力及其应变量影响较敏感，但对初始弹性模量影响极小，如抗拉强度、黏聚力等细观参数(见图5、图6)。

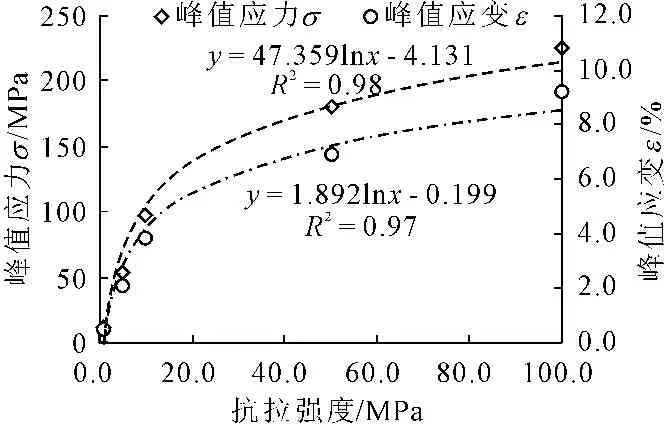
图5抗拉强度与峰值应力及其对应的应变值的关系

由图5知，随着抗拉强度值变大，峰值应力值呈变大的趋势，但增幅逐渐减小，拟合抗拉强度和峰值应力的变化关系如下：

(1)

由图5还知，随着抗拉强度值变大，峰值应力对应的应变值同样呈变大趋势，拟合两者的变化关系如下：

(2)

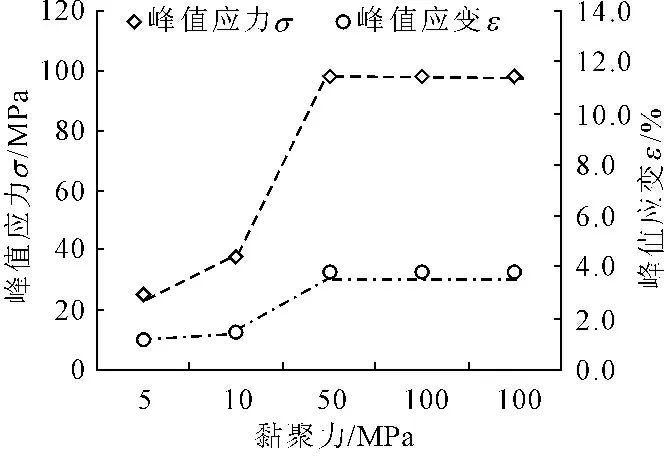
图6黏聚力与峰值应力及其对应的应变值的关系

由图6可知，黏聚力取值50 MPa时为黏聚力与峰值应力及其对应的应变值的变化趋势的一个转折点：当黏聚力小于50 MPa时，随黏聚力值的变大，峰值应力呈变大趋势。当黏聚力大于或等于50 MPa后，随黏聚力值的变大，峰值应力的取值始终保持在98.0 MPa附近不变。

峰值应力所对应的应变量有类似的规律：当黏聚力大于或等于50 MPa后，随黏聚力值的变大，峰值应力对应的应变量始终保持在3.85%附近不变。

Ⅱ类：具有复合影响效果，对应力峰值和初始弹性模量E0均为敏感，如等效模量、黏性等效模量以及黏性刚度比等细观参数(见图7、图8、图9)。

由于Ⅰ类细观参数仅对峰值应力及其对应的应变量敏感，因此在分析Ⅱ类细观参数对应力-应变曲线特征量的敏感性时，可利用Ⅰ类细观参数的特性，化Ⅱ类复合型影响效果为单因素影响进行分析，仅分析Ⅱ类细观参数对初始弹性模量的E0影响效果。

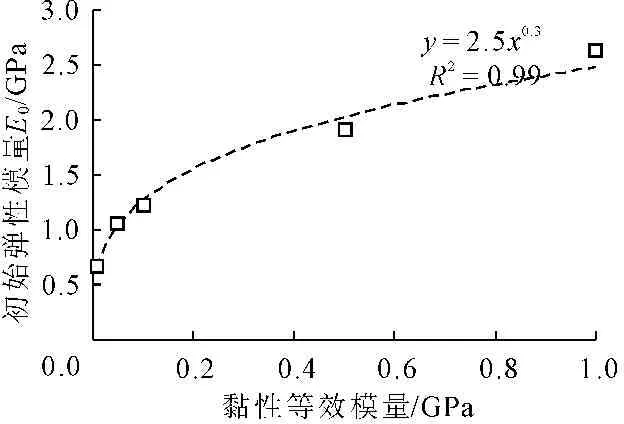
图7 等效模量与初始弹性模量E0的关系

图8黏性等效模量与初始弹性模量E0的关系

随着等效模量取值的变大，初始弹性模量相应增加，拟合的表达式为：

E0=2.5E*0.3

(3)

由图8可知，黏性等效模量与初始弹性模量之间拟合的关系表达式为：

(4)

(5)

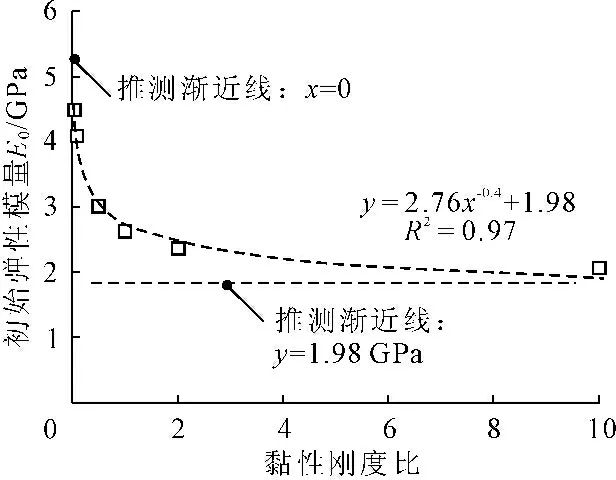
图9黏性刚度比与初始弹性模量E0的关系

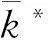
(6)

Ⅲ类：对应力-应变曲线中各特征值均不敏感，如刚度比、摩擦系数等细观参数。

Ⅳ类：对试样破坏形式敏感，如摩擦角(见图10、图11)。

由图10可知，在本次细观参数取值范围内，试样中的接触破坏既有由张拉破坏导致的接触断裂，又有由剪切破坏导致的接触断裂。当摩擦角取值不同时，试样的破坏形式可以分为如下三种：

(1) 摩擦角取值0°、45°、180°、225°、360°时，颗粒间的接触属性均表现为受拉断裂，且断裂时应变量较大。

(2) 摩擦角取值135°、315°时，颗粒间的接触属性均为受拉断裂，且断裂时应变量较小。

(3) 摩擦角取值90°、270°时，颗粒间的接触属性绝大部分表现为剪切破坏。此外，颗粒间的接触最先出现受剪断裂，并且断裂时应变量极小。

图10摩擦角不同取值下的试样破碎情况

单轴试验条件下试验发生破坏有两个关键性节点：一个是颗粒间的接触属性第一次发生破坏，即初始破坏；另一个是颗粒间的接触属性大面积发生破坏且相互贯通，此时试样承载能力突然减小，即瞬间断裂。下面分析颗粒间的接触属性在初始破坏和瞬间断裂时所对应的应变之间的关系。

图11接触破坏突变值对应的试样应变量对比

由图11可知，总结如下几点规律：

(1) 从初始破坏到瞬间断裂所经历的应变量差值不大，在本试验条件下其破坏过程的应变量差值约为1.65%～2.54%。

(2) 随着摩擦角的增大，该破坏过程表现出一定的周期性，且周期为180°。

2 细观参数取值方法及验证

2.1 细观参数取值方法

根据上述不同细观参数对试样应力-应变曲线影响效果及特点，制定细观参数配选的思路见图12。

图12确定细观参数取值的思路

(1) 拟合初始弹性模量E0。根据试验室岩石单轴试验所得初始弹性模量E0，即可确定等效模量的数量级。通常在没有其他参考条件的前提下，近似地取等效黏性弹性模量和等效模量的值相等。此外，结合非零的黏性刚度比与初始弹性模量E0之间的数值关系，与等效模量(emod)以及黏性等效模量(pb_emod)相互配合可迅速确定Ⅱ类细观参数的取值，即可完成对应力-应变曲线中的初始弹性模量E0的拟合。

(2) 拟合峰值应力及其对应的应变量。在完成初始弹性模量E0的拟合后，利用Ⅰ类细观参数对应力-应变曲线中的初始弹性模量E0不敏感的特性，同时结合抗拉强度和黏聚力与应力峰值及其对应的应变量的数学关系，完成对应力-应变曲线的峰值及其对应的应变量等特征值的拟合。此时，Ⅰ、Ⅱ类细观参数的取值基本确定，应力-应变曲线基本拟合完毕。

(3) 破坏模式调整。由于摩擦角对颗粒间接触属性破坏形式敏感，通过调试摩擦角的取值，调节试样的破坏形式。虽然相较于上一个参数调试步骤，此时所得模拟结果的应力-应变曲线会有轻微的改变，但是总体影响不大。

(4) 结果微调。为了弥补上一个拟合步骤所导致的轻微变化，可以通过调整刚度比和摩擦系数等Ⅳ类细观参数的取值，从而达到结果微调的目的。

2.2 实例验证

利用2.1节细观参数的选取方法，对砂岩岩石试样的细观参数进行拟定，具体取值见表2。

室内砂岩单轴试验结果和本文细观参数取值条件下的PFC模拟结果进行对比，如图13所示(图13中室内试验数据引自文献[18])。

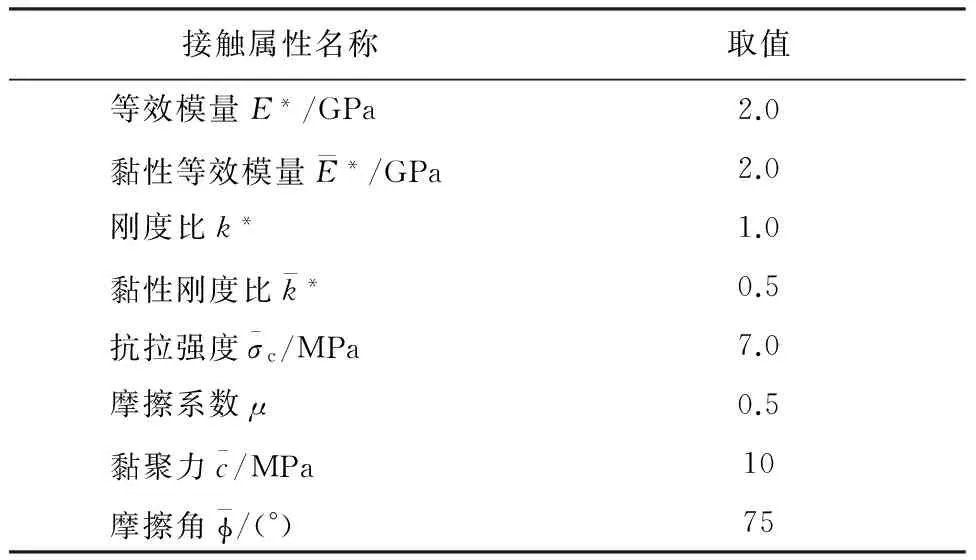
表2 砂岩细观参数取值表

图13砂岩室内单轴试验和数值模拟的应力-应变曲线对比

由图13可知，试验室中的砂岩试样在压缩初期，其应力-应变曲线会出现先缓后陡的现象。一方面可能是砂岩试样受压后，其天然缝隙闭合的一个过程；另一方面也可能是砂岩试样由于制样过程导致的卸载回弹，而被再次压缩导致的。基于上述因素导致的初始弹性模量的不确定性，取岩石试样轴向应变为1%处的应力-应变曲线进行拟合确定。因此，在运用本方法确定的细观参数的基础上，对应力-应变曲线中的初始弹性模量E0、应力峰值及其对应的应变量等特征值的拟合效果均表现良好。

试样破坏形式的对照情况如图14所示(图中室内岩石破坏图像引自文献[18])：

图14砂岩破坏形式的室内试验和数值模拟结果

本文细观参数取值条件下的PFC2D单轴试验模拟结果表明，裂缝开展的角度大约在40°～55°范围，表现出拉、剪破坏相结合的断裂形式，与室内试验结果相互吻合。

3 结 语

本文通过大量的试验模拟计算，研究线性平行粘结接触模型中的接触属性与应力-应变曲线特征量之间的数学关系，得到了以下结论：

(1) 根据线性平行粘结接触模型中的细观参数对应力-应变曲线特性以及试样破坏形式的影响情况，将细观参数分为四类：① 对峰值应力及其应变量影响较敏感，但对初始弹性模量影响极小，如抗拉强度、黏聚力等细观参数；② 具有复合影响效果，对应力峰值和初始弹性模量E0均为敏感，如等效模量、黏性等效模量以及黏性刚度比等细观参数；③ 对应力-应变曲线的各特征值均不敏感，如刚度比、摩擦系数等细观参数；④ 对试样破坏形式敏感，如摩擦角。

(2) 以线性平行粘结接触模型中的细观参数对应力-应变曲线影响的特征为基础，结合试样破坏形式，制定的岩石细观参数的选取方法，能够较大程度上缩短初次确定岩石细观参数的时间，并且通过实例验证表明所得应力-应变曲线以及试样破坏模式等各方面的模拟效果均表现良好。

然而，本文提出的岩石类细观参数取值办法，虽然能在较大程度上缩短初次确定岩石细观参数的时间，但是，在细观参数取值过程中，由于具有复合影响效果的细观参数，如Ⅱ类细观参数，其宏细观参数之间具有极其复杂的物理力学关系，很难建立起统一的数学关系。本文在拟合Ⅱ类细观参数的过程中，采取化Ⅱ类复合型影响效果为单因素影响效果考虑的方式，必然会导致一定量的试算过程，无法做到一步到位。

[1] Billaux D, Dedecker F, Cundall P. A novel approach to studying rock damage: the three-dimensional adaptive continuum/discontimuum code[C]//Proceedings of Eurock 2004 & 53rd Geomechanics Colloquium, 2004:723-728.

[2] 朱焕春，Andrieux Patrick，钟辉亚.节理岩体数值计算方法及其应用(二):工程应用[J].岩石力学与工程学报,2005,24(1):89-96.

[3] 常晓林,胡 超,马 刚,等.模拟岩石失效全过程的连续-非连续变形体离散元方法及应用[J].岩石力学与工程学报,2011,30(10):2004-2011.

[4] 曹琰波,戴福初,许 冲,等.唐家山滑坡变形运动机制的离散元模拟[J].岩石力学与工程学报,2011,30(S1):2878-2887.

[5] 王念秦,汤廉超.黄土崩塌灾害运动机理及其离散元数值模拟研究[J].水利与建筑工程学报,2016,14(2):152-156.

[6] 王 涛,陈晓玲,杨 建.基于3DGIS和3DEC的地下洞室围岩稳定性研究[J].岩石力学与工程学报,2005,24(19):3476-3481.

[7] 蒋明镜,周雅萍,朱方园,等.素混凝土桩复合地基承载机理的离散元分析[J].水利与建筑工程学报,2012,10(3):1-7.

[8] Huank H Y. Discrete element modeling of tool rock interaction[D]. Minnesota: University of Minnesota, 1999.

[9] Nardin A, Schrefler B A. Modelling of cutting tool soil interaction part II: macromechanical model and upscaling[J]. Computer Mechanics, 2005,36(5):343-359.

[10] Hsieh Y M, Li H H, Huang T H, et al. Interpretations on how the macroscopic mechanical behavior of sandstone affected by microscopic properties—revealed by bonded particle model[J]. Engineering Geology, 2008,99(1/2):1-10.

[11] 徐金明,谢芝蕾,贾海涛.石灰岩细观力学特性的颗粒流模拟[J].岩土力学,2010,31(S2):390-395.

[12] 丛 宇,王在泉,郑颖人,等.基于颗粒流原理的岩石类材料细观参数的试验研究[J].岩土工程学报,2015,37(6):1031-1040.

[13] 赵国彦,戴 兵,马 驰.平行黏结模型中细观参数对宏观特性影响研究[J].岩石力学与工程学报,2012,31(7):1491-1498.

[14] 周 健,杨永香,刘 洋,等.循环荷载下砂土液化特性颗粒流数值模拟[J].岩土力学,2009,30(4):1083-1088.

[15] 尹成薇,梁 冰,姜利国.基于颗粒流方法的砂土宏-细观参数关系分析[J].煤炭学报,2011,36(S2):264-267.

[16] 徐小敏,凌道盛,陈云敏,等.基于线性接触模型的颗粒材料细-宏观弹性常数相关关系研究[J].岩土工程学报,2011,32(7):991-998.

[17] 曹 智.砂泥岩及其颗粒料力学特性PFC模拟方法研究[D].重庆:重庆交通大学,2016.

[18] 王俊杰,方绪顺，邱珍锋，等.砂泥岩颗粒混合料工程特性研究[M].北京:科学出版社,2016.

SelectionMethodsofRockMicro-parametersBasedontheLinearParallelBondContactModel

LIU Liangjun1, CAO Zhi2, WANG Junjie3,4

(1.ChongqingTengyunEngineeringConsultantCo.,Ltd.,Chongqing400020,China；2.Hu'nanHydro&PowerDesignInstitute，Changsha，Hu'nan410007,China；3.NationalEngineeringResearchCenterforInlandWaterwayRegulation,ChongqingJiaotongUniversity,Chongqing400074,China；4.KeyLaboratoryofHydraulicandWaterwayEngineeringoftheMinistryofEducation,ChongqingJiaotongUniversity,Chongqing400074,China)

The PFC2Dmodel of rock sample is developed based on the linear parallel bond contact model. Micro-parameters is divided into four categories upon the foundation of the correspondence relationship between micro-parameters and macro-properties. Micro-parameters named class I have little influence on initial elastic modulus, but have obvious impacts on the peak stress and its strain. Micro-parameters named class II have marked impacts on initial elastic modulus, peak stress and its strain. Micro-parameters named class III have little influence on the characteristic stress-strain curves. Micro-parameters named class IV have great impacts on damage form of rock sample. The dissimilarities on the effect of micro-parameters to macro-properties are used, and the selection method of rock micro-parameters is produced as detailed below. Fitting the initial elastic modulusE0; Fitting the peak stress and its strain; Adjusting the damage form; Fine-tuning the result.

rock;micro-parameter;thelinearparallelbondcontactmodel;numericalsimulation

10.3969/j.issn.1672-1144.2017.05.021

2017-05-24

2017-06-21

国家自然科学基金项目(51479012)

刘良军(1976—)，男，重庆人，高级工程师，主要从事水利水电建筑工程、水工结构设计方面的研究。 E-mail: 26687726@qq.com

TU458

A

1672—1144(2017)05—0123—06