基于DMC-PID控制的催化剂温控系统设计
李红利 李献民
(天津工业大学电气工程与自动化学院)
基于DMC-PID控制的催化剂温控系统设计
李红利 李献民
(天津工业大学电气工程与自动化学院)
通过对动态矩阵控制(DMC)算法和传统PID控制的分析,提出一个基于DMC-PID串级控制的催化剂温控系统。仿真结果表明:DMC-PID控制效果优于PID-PID控制;电流副回路采用PID控制,能够快速有效调节电流进而控制燃烧炉内温度;温度主回路采用DMC控制,克服了传统温控系统存在的超调量大、时延及滞后性等问题,避免了多种不可测扰动的影响。
催化剂温控系统 DMC-PID串级控制 仿真分析 Matlab
湿焙回转炉催化剂温控系统通过调节电加热器电流来控制燃烧室温度。温控过程热惯性大、耦合性强,电流易受周围电磁场干扰,导致系统很难建立准确的数学模型。传统的催化剂温控系统采用PID单回路控制,存在超调量大、稳定时间长、时延大及滞后大等问题[1]。
动态矩阵控制(Dynamic Matrix Control,DMC)虽然能够预测被控模型,但其采样周期大、抗干扰能力差。因此,笔者将DMC与PID结合,设计了一个基于DMC-PID串级控制的催化剂温控系统,针对不同被控对象予以分级处理,通过过程数据和变化趋势预测控制器输出。
1 工艺过程与方案分析
以湿焙回转炉催化剂温度为被控变量,现场工艺如图1所示。除尘器吹扫物料完毕后,通过下料阀送到给料机,引风机控制压力阀调节尾气压力。调节电加热器参数控制回转炉温度,物料在回转炉中循环加热。当出料温度过高时,经由冷却水回路降温;出料温度过低时,经由过热蒸汽回路加热[2]。催化剂温度是化工生产过程中的重要参数,必须控制在1 000±50℃,且超调量要尽可能小甚至是无超调。由于催化剂生产要求温度较高,升温过程中存在严重的滞后性和延时性,导致上位机采集到的数据无法实时有效反映现场的实际温度。

图1 湿焙回转炉催化剂温度控制工艺
物料温度与电流成非线性关系,传统的PID控制无法适用于催化剂温控系统。同时,催化剂温控过程受多种因素影响,难以建立准确的数学模型。因此,笔者提出了一种DMC-PID串级控制方式(图2)。副回路采用PID控制,通过调节三相电流来控制燃烧室温度;主回路采用DMC,以解决温控系统滞后性、时延性等问题。DMC适用于复杂的工业控制系统,根据实测的阶跃响应离散系数,利用最小二乘法辨识得到与催化剂温控过程相似的预测模型[3]。控制器采集当前温度和过去温度的偏差值,预测升温过程未来的偏差值,以滚动优化确定当前的最优输入策略[4]。同时,通过反馈校正实际输出和预测模型输出之间的误差,利用实际数据校正预测模型。
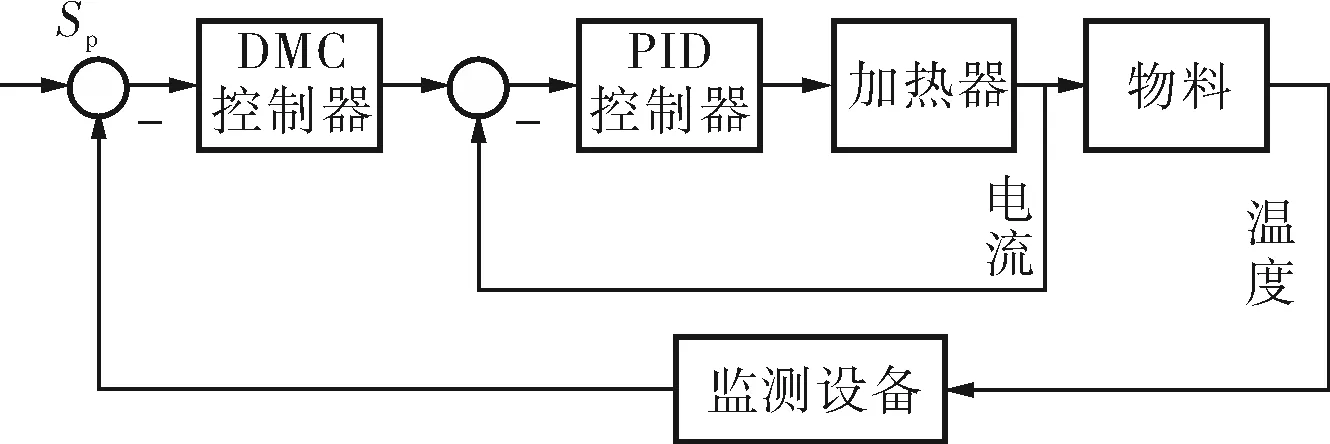
图2 催化剂温控系统控制方案
2 温度的DMC策略
2.1 问题的提出
DMC算法注重模型功能,对被控过程的模型精度要求不高。因此,通过对加热过程和现场数据进行分析,采用最小二乘法中的系统辨识方法得到催化剂温控系统的近似模型。选取加热器电流和催化剂温度作为被控变量,对应的输入输出分别为U(s)和Y(s)。根据被控对象的实测特性,电流副回路为一个惯性环节,温度主回路为一个大惯性环节(近似为积分环节)。考虑到温度的大滞后性和时延性,催化剂加热过程的近似数学模型为一个含一阶积分单输入单输出的闭环控制系统,即:


现场测取数据分析,每3min采样一次,持续记录5h系统在闭环状态下的温度变化过程,数据经整定归一化处理后,利用模式识别方法得到的近似数学模型为:

2.2 DMC算法
DMC算法是一种基于被控对象阶跃响应的预测控制算法,不要求被控对象的参数精度,即可实现高质量控制,其原理如图3所示。通过对被控对象进行一阶响应,获得离散系数模型;应用系统辨识法,预测传递函数类型[5]。该算法采用多步预估技术,解决了时延、滞后造成的影响,并能够按预估输出与给定值的偏差校正预测模型。

图3 DMC算法原理
2.2.1 预测模型
被控对象为阶跃响应,a1,a2,…,aN为系统阶跃响应动态系数,即阶跃响应在采样时间t=T,2T,…,NT时的值;N为阶跃响应截断点[6]。利用阶跃响应的动态系数和给定的输入控制增量即可得到预测模型方程:
YM(k+1)=Yn(k+1)+AΔU(k)
=ΔU(k)+A0U(k-1)
Ym(k+1)=[Ym(k+1/k),Ym(k+2/k),…,Ym(k+p/k)]T
Y0(k+1)=[Y0(k+1/k),Y0(k+2/k),…,Y0(k+p/k)]T
ΔU(k)=[Δu(k),Δu(k+1),…,Δu(k+m-1)]T
U(k-1)=[u(k-N-1),u(k-N-2),…,u(k-1)]T
该模型反映了未来输出预测值、动态矩阵A和未来控制输入三者之间的关系。
2.2.2 滚动优化
预测控制的控制策略是滚动优化、滚动实施和在线校正。优化过程是反复在线进行的,优化目标随时间推移而变换。
为柔化控制、增强鲁棒性,在输入端接入输入滤波器。参考轨迹为:
YR(k+i)=GR(z-1)w(k)
最优控制规律由二次型性能指标确定,即:
Jp=[Yp(k+1)-YR(k+1)]TQ[Yp(k+1)-
YR(k+1)]+UT(k)RΔU(k)
其中,Q、R为输出预测误差加权阵和控制量加权阵。令∂Jp/∂U(k)=0,则当前控制策略k时刻的控制增量为:
ΔU(k)=(1,0,…,0)(ATQA+R)-1ATQ[YR(k+1)-
A0U(k-1)-he(k)]
=dT[YR(k+1)-A0U(k-1)-he(k)]
dT=[d1,d2,…,dp]=cT(ATQA+R)-1ATQ
cT=[1,0,…,0]
2.2.3 反馈校正
由于模型误差、干扰等因素的影响,系统输出预测值需要不断根据实际输出值进行修正[7],则有:
Yp(k+1)=Ym(k+1)+h[y(k)-ym(k)]
=AΔU(k)-A0U(k-1)+he(k)
Yp(k+1)=[Yp(k+1),Yp(k+2),…,
Yp(k+p]Te(k)
=y(k)-ym(k)
h=[h1,h2,…,hp]T
2.3 DMC控制器
催化剂加热过程温度环节主要由DMC控制器完成,DMC控制器控制过程主要包括在线和离线两个环节[8]。在线算法流程如图4所示,由初始化模块和实时控制模块组成。离线过程包括模型识别、计算控制系数d和选择校正系数h1,…,hN。

图4 在线算法流程
3 仿真与结果分析
为验证预测模型的实用性,利用Matlab中的M文件编辑DMC-PID串级控制器来仿真催化剂加热过程,并将仿真结果与现场控制器实际设定参数的控制效果进行对比。现场工业生产中,通过PID参数调节加热器电流来控制回转炉内不同分区的炉温,通过DMC参数来调节控制效果的实时性和稳定性。DMC调节是在PID调节基础上的进一步优化,是温控系统中最重要的环节[9]。DMC的设计参数主要包括采样周期T、最优时域长度P、控制时域长度M、Q、R及误差校正矢量h等[10]。催化剂温控系统具有强耦合性和强干扰性,加热过程存在电磁场影响电流等不可测误差,故在控制过程中必须考虑不可测误差的干扰。
为预估不可测误差对温控系统的影响,设置一个积分旋转因子a=-0.23。仿真过程中DMC参数为:T=120s,P=20,M=1,Q取值全为14,R取值全为10,模拟时域长度N′=100。DMC-PID仿真效果如图5所示。
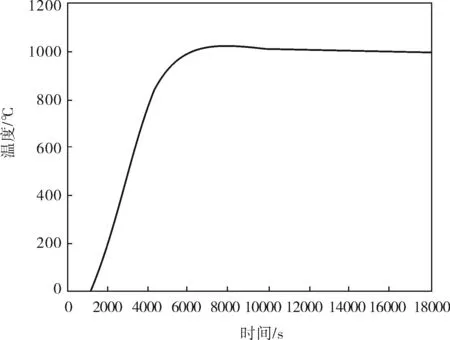
图5 DMC-PID仿真效果
为验证DMC-PID串级控制效果的优越性,在催化剂温控系统中采用PID-PID控制方案(电流副回路和温度主回路均采用PID控制方式)进行对比分析。利用Simulink构建仿真模型,调节PID参数,得到仿真效果如图6所示。PID-PID控制下系统超调量大,导致温度联锁,加热器自动停止加热,下一步工艺无法进行,不符合系统要求。同时,PID-PID控制要求系统具有精确的控制模型和参数,而催化剂加热过程复杂,不可测扰动多,使得控制曲线出现较大振荡,直接影响控制精度[11]。因此,PID-PID控制方案无法达到催化剂温控系统的要求。

图6 PID-PID仿真效果
4 结束语
笔者将DMC算法与PID控制结合,设计了一个基于DMC-PID串级控制的催化剂温控系统。仿真结果表明,DMC-PID算法既保持了串级控制结构的优点,与PID-PID串级控制相比,又表现出了更为优越的综合性能。电流副回路采用PID控制,能够快速有效调节电流进而控制燃烧炉内温度,抗干扰能力强;温度主回路采用DMC控制,克服了传统温控系统存在的时延、热惯性大、滞后性及非线性等不良特性,避免了多种不可测扰动的影响。
[1] 何佳佳,侯再恩.PID参数优化算法[J].化工自动化及仪表,2010,37(11):1~4.
[2] 郭伟,陈琛,陆振宇.一种改进型动态矩阵控制在水箱液位系统中的应用[J].计算机测量与控制,2015,23(5):1563~1567.
[3] 吕亚锋,郭利进,成立存.基于动态矩阵控制的聚合釜温度控制与仿真[J].计算机仿真,2014,31(7):198~201.
[4] 许超,陈治纲,邵惠鹤.预测控制技术及应用发展综述[J].化工自动化及仪表,2002,29(3):1~10.
[5] 米一博,石红瑞.模糊PID算法在温度对象中的应用[J].石油化工自动化,2016,52(4):29~31.
[6] 张诗桂,朱立新,赵义正.粒子滤波算法研究现状与发展趋势[J].电子信息对抗技术,2010,25(5):8~16.
[7]RuizfemeniaR,FlorestlacuahuacA,GrossmannIE.Logic-BasedOuter-ApproximationAlgorithmforSolvingDiscrete-ContinuousDynamicOptimizationProblems[J].Industrial&EngineeringChemistryResearch,2012,53(13): 5067~5080.
[8]CvejnJ.TheDesignofPIDControllerforNon-OscillatingTime-DelayedPlantswithGuaranteedStabilityMarginBasedontheModulusOptimumCriterion[J].JournalofProcessControl,2013,23(4):570~584.
[9]BobalV,KubalcikM,DostalP,etal.AdaptivePredictiveControlofTime-DelaySystems[J].Computers&MathematicswithApplications,2013,66(2):165~176.
[10]Romero-GarcíaJM,GuzmánJL,MorenoJC,etal.FilteredSmithPredictortoControlpHduringEnzymaticHydrolysisofMicroalgaetoProduceL-AminoacidsConcentrates[J].ChemicalEngineeringScience,2012,82(1):121~131.

DesignofCatalystTemperatureControlSystemBasedonDMC-PIDControl
LI Hong-li, LI Xian-min
(CollegeofElectricalEngineeringandAutomation,TianjinPolytechnicUniversity)
Through analyzing dynamic matrix control (DMC) and traditional PID control, a DMC-PID cascade control-based catalyst temperature control system was proposed. The simulation results show that, the DMC-PID cascade control outperforms PID control; and adopting PID control in the current’s minor loop can rapidly and effectively adjust the current to control temperature within the combustion furnace; and adopting DMC con-
TH862
A
1000-3932(2017)01-0065-05
(Continued on Page 110)
李红利(1978-),副教授,从事神经信息的非线性动力学分析、工业过程控制等研究工作。
联 系 人:李献民(1989-),硕士研究生,从事工控系统方面的研究,269499515@qq.com。
2016-07-03,
2016-07-31)

