一个考虑浅层地下水位埋深的降雨物理入渗模型
豆红强, 蒋森辉
(福州大学环境与资源学院, 福建 福州 350116)
一个考虑浅层地下水位埋深的降雨物理入渗模型
豆红强, 蒋森辉
(福州大学环境与资源学院, 福建 福州 350116)
基于经典Green-Ampt 入渗模型, 建立了考虑任意降雨强度下浅层地下水位埋深的降雨物理入渗模型. 针对4种不同渗透性质的土样, 将此模型的解析解与数值模拟结果进行对比分析, 结果表明: 所建的降雨入渗物理模型及其数值解的最大积水时差仅为0.274 h, 最大相对累积入渗量误差仅为3.204%, 验证了该修正模型的合理性. 同时以砂质壤土为例, 利用该模型分析不同地下水位埋深对降雨入渗的影响. 分析表明: 雨水入渗速率、 累积入渗量以及积水时间受地下水位埋深的影响较小, 而湿润锋深度随着降雨历时的增加受其影响逐渐明显.
降雨入渗; Green-Ampt 模型; 地下水位; 非饱和土; 物理入渗模型
0 引 言
降雨入渗是指雨水通过地表向下运动补给土壤水、 地下水, 是水分在土体中的一个动态分布过程, 更是土壤水分循环的重要组成部分. 降雨入渗的研究对农田灌溉与排水、 地下水补给、 土壤侵蚀以及边坡的稳定性等均有至关重要的作用.
相较于数值解的收敛存在严重的参数敏感性(例如, 非饱和渗流求解过程中的数值弥散现象[1]和非线性迭代收敛震荡[2]等), 建立一种简单、 物理基础明确且能准确反映降雨入渗的模型是研究此类问题的有效方法. Green和Ampt[3]以毛管理论为基础, 提出具有相同初始含水量的均质土壤的下渗方程(Green-Ampt 模型), Mein 和Larson[4]将其推广到稳定降雨入渗的情况, Chu[5]又将此模型推广应用于自然变雨强的雨水入渗过程. 而后, 众多学者针对不同工况发展了经典Green-Ampt入渗模型. 如, 韩同春等[6]基于Green-Ampt入渗模型建立了考虑土体中封闭气压影响的扩展入渗模型. 李秀珍等[7]扩展了Mein-Larson模型, 使其能够考虑高强度短历时和低强度长历时的两种降雨工况. 范严伟等[8]建立了改进的夹砂层土壤的Green-Ampt 入渗模型. Cho[9]采用扩展Green-Ampt入渗模型模拟了浅层残积土边坡下端为不透水基岩的工况. 但上述入渗模型均假设土壤剖面的初始含水量为均匀分布的半无限体, 显然, 当地表下存在埋深较浅的地下水位时, 地下水位线以上的土壤剖面的含水量必然呈非线性分布. 也就是说, 以上扩展入渗模型大都针对理想化的工况, 而未能考虑地下水位埋深对雨水入渗的影响.
詹良通等[10]基于非饱和渗流控制方程, 建立了考虑地下水位埋深情况下的雨水入渗无限长斜坡内水分运移模型. Lu等[11]基于非饱和土达西渗流定律, 求解了以地下水位为边界条件的土壤剖面内基质吸力分布的解析解. 但是以上解析解均假设雨水全部入渗到土壤剖面中, 即以上方程仅能考虑降雨强度小于土体饱和渗透系数(r
实际上, 李宁等[12]已基于非线性Richards方程, 采用Fourier积分变换分别针对降雨强度大于和小于饱和渗透系数的两种工况, 推导出斜坡入渗解析解的统一表达式, 并通过与数值解的对比验证了此解析解的正确性. 相较于求解Richards方程的解析解, 土壤入渗物理模型具有概念明确、 简便有效、 便于在工程中应用的特点, 因此土壤入渗物理模型不失为一种解决非饱和土雨水入渗的简单而有效的方法.
为此, 本研究主要包括: 1) 从经典Green-Ampt入渗模型角度出发, 建立一个任意雨强下考虑地下水位埋深的降雨入渗模型; 2) 针对4种不同类型的土样, 将由此模型所得的雨水累积入渗量和雨水入渗率与数值解(Richards方程)进行对比分析, 以验证此改进模型的合理性; 3) 利用此改进模型分析地下水位埋深对非饱和土体降雨入渗的影响.
1 考虑地下水位埋深的降雨入渗物理模型
1.1 Green-Ampt入渗模型
由于所建立的强降雨条件下考虑地下水位埋深的雨水入渗模型是经典Green-Ampt入渗模型的扩展, 因此有必要对Green-Ampt入渗模型作简要的介绍.
Green与Ampt 基于毛管理论提出具有相同初始含水量的均质土壤的下渗方程. 其入渗率为:
式中:f为土壤入渗率, cm·h-1;ks为饱和土渗透系数, cm·h-1;Sf为湿润锋处概化基质吸力, cm;zf为概化的湿润锋深度, cm;h为地表处的总水势, cm.
当表面积水很少时, 即h≈0时, 根据入渗量F(t)与入渗率f(t)的关系, 可得:
式中:F为累计入渗量; Δθ=θs-θi, 为含水率之差.
Mein与Larson将Green-Ampt模型推广应用至稳定降雨入渗的情况, 其将雨水入渗过程分为水头控制入渗和流量控制入渗两个阶段, 两阶段的分界点为降雨强度i等于土壤入渗率f, 此后地表开始积水或产生径流, 设积水时刻为tp, 此时降雨强度i等于雨水入渗率f, 则由Green-Ampt模型可知积水时刻的所对应的累积入渗量为:
式中:θs为土体饱和体积含水率;θi为土体初始体积含水率.
同时, 整个入渗过程的入渗率可表示为:
则上式可写为累积入渗量F与时间t的显式方程:
1.2 考虑地下水位埋深的扩展降雨入渗模型
当地表下存在埋深较浅的地下水位时, 则地下水位线以上土壤剖面的含水量呈非线性分布. 设地下水位埋深为h, 则有:
其中:z为位置水头,ψ为位置水头z处所对应的基质吸力.
此时为确定土壤剖面初始含水率的分布, 必须确定体积含水率与基质吸力之间的关系. 采用Brook与Corey[13]所提出的土水特征曲线拟合公式:
联立式(5)和(6), 即可得地下水位以上土壤剖面的初始含水率分布为:
当降雨强度小于土壤饱和渗透系数时(i
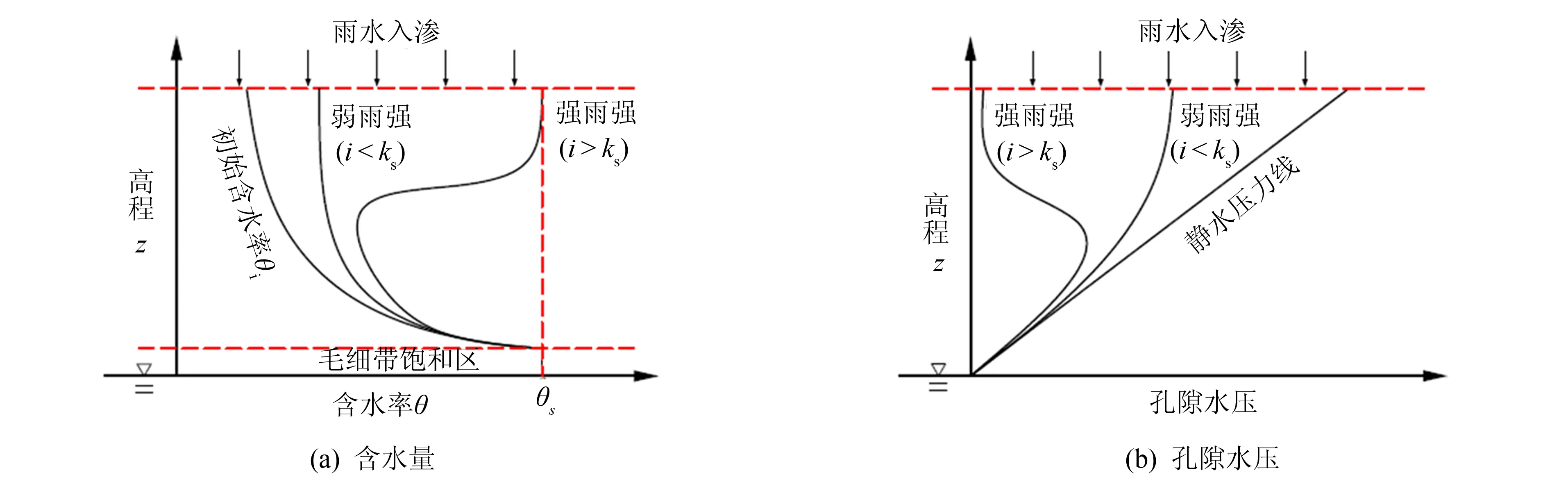
图1 土体剖面含水率及孔隙水压分布示意图Fig.1 Schematic diagram of conceptual water content and pore pressure profile
由Green-Ampt入渗模型可知, 当t=tp时, 必然有降雨强度等于土壤入渗速率, 即:
式中:zp为积水时所对应的湿润锋深度.
设积水时刻所对应的累积入渗量为Fp, 由于入渗雨水质量守恒, 则有:
将式(8)代入式(10), 可得:
则对应的积水时刻为:
当t>tp时, 设累积入渗量为F, 此时对应的湿润锋深度为z, 则沿湿润锋深度积分得:
将其化为微分形式, 则:
将式(8)代入式(14) 并化简得:
因此, 由式(9), (15)可知, 求解积水时刻tp以及累积入渗量F(t)的关键在于确定湿润锋处概化基质吸力Sf. 由于此时土壤剖面中初始含水率θi呈非线性分布, 则上式中湿润锋处概化基质吸力Sf不再为一常量, 而是随湿润锋深度z变化的函数.
实际上, 早在1964年, Bouwer[14]认为概化湿润锋吸力Sf可表示为非饱和土壤导水率的函数, 即:
但上式并非基于理论推导得出, 而是将模拟水平流动的结果用于垂直情况.
Mein与Larson[4]提出用土壤水吸力的加权平均值来表示, 即:
式中:kr为相对渗透系数,kr=k(θ)/ks.
Moore等[15]将上述湿润锋处概化基质吸力Sf修正为:
且研究表明, 相对于(θs-θi)所引起的误差,Sf引起的误差较小.
通过比较分析, 采用式(18)来计算Sf, 则联立式(5)、 (6)、 (7)和(17)可得:
式(18)即表示了在地下水位埋深为h,Sf为湿润锋深度z的函数. 显然, 当土壤剖面的初始含水率沿深度方向θi为一常量时, 此时对应的Sf亦为一常量, 式(9)和(15)也可退化为经典的Green-Ampt入渗模型.
一旦确定了Sf, 就可以通过式(9)采用相应的迭代程序求解出积水时刻所对应的湿润锋深度z,进而求出相对应的积水时间tp; 最后通过四阶Runge-Kutta法即可求解微分方程(15)以确定z(t).
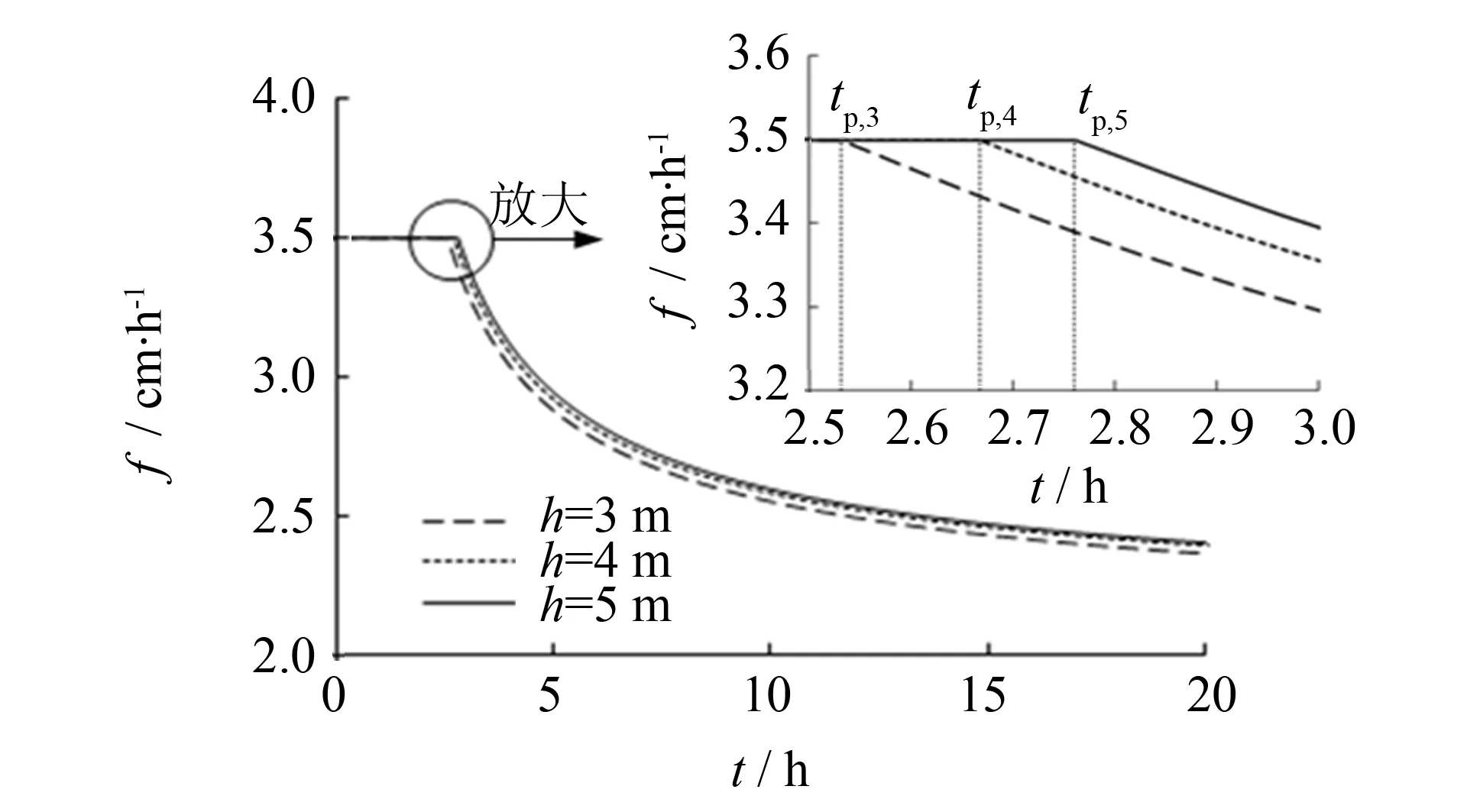
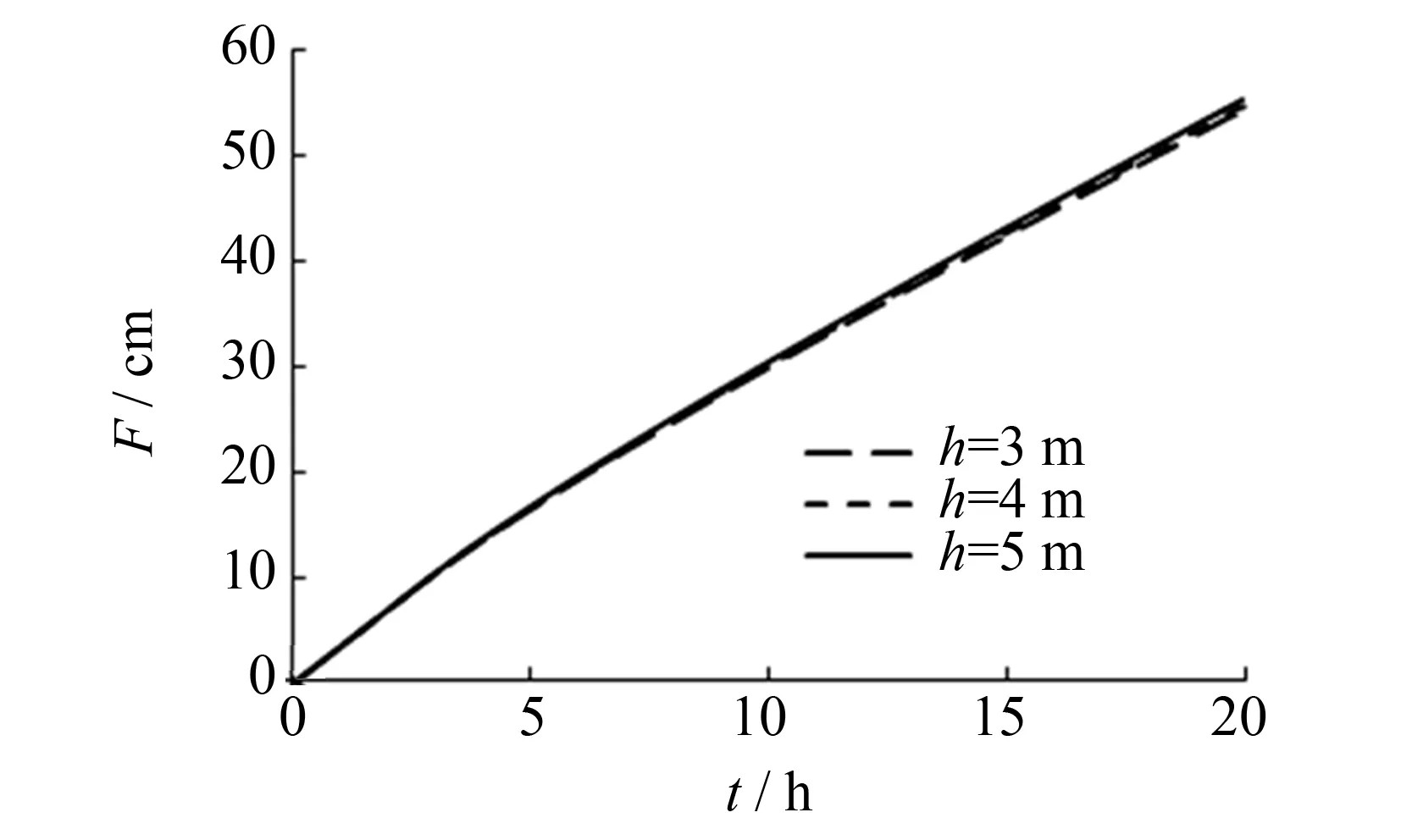
另一方面, 当降雨强度i小于土体饱和渗透系数时(i 此时湿润锋上部土体的含水率不再为饱和含水率θs, 设此时对应的含水率为θ0, 则根据非饱和土Darcy定律, 知: 则沿湿润锋深度方向积分, 得: 由于Green-Ampt入渗模型的剖面含水量剖面为矩形剖面, 则式(22)可简化为: 显然,θ0可由式(7)与(23) 通过牛顿迭代法确定. 值得注意的是, 所建模型的适应范围可以扩展到土壤剖面初始含水率呈任意分布的情形, 因为一旦确定了土壤剖面初始含水率的分布, 由式(18)即可确定湿润锋处概化基质吸力Sf(z), 进而结合本改进的Green-Ampt入渗模型即可求解出非饱和土在雨水入渗情况下的入渗率以及累积入渗量. 为验证所得改进的雨水入渗模型的正确性, 采用Hydrus-1D对4种不同类型的一维土柱进行数值计算, 土体物理性质参数来源于Rawls等[16]所统计的近似参数, 如表1所示. 土柱计算模型深4 m, 地下水位埋深h均为3 m, 降雨持时为20 h. 边界条件为考虑地表径流的大气边界条件, 初始条件为θ=θi, 其值可由Brook-Corey土水特征曲线根据地下水位的埋深确定. 数值解的控制方程为Richards 方程: 表1 土体基本物理性质与降雨强度 图2为由本改进入渗模型和数值模型分别针对以上四种土样所计算的雨水累积入渗量和入渗速率随时间变化的曲线. 由图可知, 在地表积水前 (t 图2 累积入渗量和入渗速率与时间的关系Fig.2 Cumulative infiltration and infiltration rates versus time on four soil textures 表2为由本文改进入渗模型和数值解分别针对以上土样在降雨历时20 h后的具体计算结果. 同时定义模型解与数值解的积水时间差为Δtp, 相对累积入渗量误差为εF, 表2 模型解与数值解的比较 从表2中可以看出, 随着土体饱和渗透系数的增加, 积水时差以及相对累积入渗量大致呈上升趋势, 这是由于饱和渗透系数较大的粗质土进气值较低, 固水能力较差, 致使原入渗雨水通过湿润锋面迅速下渗. 但是, 本模型和数值解的最大积水时差仅为0.274 h, 最大相对累积入渗量误差仅为3.204%. 图3 入渗速率与时间的关系Fig.3 Infiltration rates versus time 以上已验证所建的考虑地下水位埋深的雨水入渗模型的合理性, 现利用此模型分析地下水位埋深对降雨入渗的影响. 取砂质壤土进行分析, 土体具体参数以及降雨强度见表1. 同时取地下水位埋深h分别取3、 4和5 m以进行对比分析. 图3反映了不同地下水位埋深下的雨水入渗速率与降雨持时的关系. 由图3可知, 随着地下水位埋深的增加, 雨水入渗速率仅有稍微增加; 同时积水时间tp亦从2.531 h增加到2.761 h, 增幅约为9%. 但雨水累积入渗量在不同地下水位埋深下基本保持不变, 如图4所示. 图4 累积入渗量与时间的关系Fig.4 Cumulative infiltration versus time 图5 湿润锋深度与时间的关系Fig.5 Depth of wetting front versus time 图5反映了不同地下水位埋深下湿润峰深度随时间的变化. 从图中可以看出, 地表积水后, 土壤剖面内湿润锋深度随地下水位埋深的增加逐渐降低, 且随着降雨持时的增加, 受地下水位埋深影响的湿润锋深度的差异逐渐明显. 具体而言, 当降雨持时达到20 h时, 地下水位埋深为3 m所对应的湿润锋深度约为248.13 cm, 地下水位埋深为5 m所对应的湿润锋深度为209 cm, 降幅达18%之多. 这是由于湿润锋的深度主要取决于土壤剖面初始含水量和雨水累积入渗量(式(8)和(14)), 而地下水位埋深的变化恰恰改变了土壤剖面初始含水量的分布. 1) 基于经典Green-Ampt入渗模型, 建立了任意雨强下考虑浅层地下水位埋深影响的降雨入渗模型(未考虑在长历时降雨条件下湿润锋与地下水位相遇的情况). 实际上, 该改进模型的适应范围可以扩展到土壤剖面初始含水率呈任意分布的情形. 然后针对粘土、 砂质粘土、 砂质粘性壤土以及砂质壤土等4种土样与数值解进行了对比分析. 结果表明: 模型解与数值解的最大积水时差仅为0.274 h, 最大相对累积入渗量误差仅为3.204%, 说明本文改进模型与数值模型有较高的吻合度. 同时, 当假设土壤剖面内初始含水率为常数时, 本文扩展模型又可以退化为经典的Green-Ampt入渗模型. 2) 针对砂质壤土探讨了地下水位埋深对降雨入渗的影响, 随着地下水位埋深从3 m增加到5 m, 雨水入渗速率仅有稍微增加, 雨水累积入渗量基本保持不变, 对应的积水时间从2.531 h增加到2.761 h, 而土壤剖面内湿润锋的深度在地表积水后随地下水位埋深的增加逐渐降低, 且随着降雨持时的增加, 受地下水位埋深影响的湿润锋深度的差异逐渐明显, 当降雨持时达到20 h时, 对应的湿润锋深度从248.13 cm降到209 cm, 降幅达18%. 3) 本研究仅针对均质土层对降雨入渗作了理论上的探讨, 实际上, 由于气象、 地质、 水文和生物过程的作用, 土壤大都呈层状结构; 另一方面, 本改进模型仅考虑了雨水入渗过程, 而忽略了雨水的蒸发、 重分布过程. 这些局限性都有待进一步的研究. [1] 吴梦喜, 高蓮士. 饱和-非饱和土体非稳定渗流数值分析[J]. 水利学报, 1999, 30(12): 38-42. [2] 陈曦, 于玉贞, 程勇刚. 非饱和渗流 Richards 方程数值求解的欠松弛方法[J]. 岩土力学, 2012, 33(增刊1): 237-243. [3] GREEN W H, AMPT G A. Studies on soil physics: flow of air and water through soils[J]. J Agric Sci, 1911, 4(1): 1-24. [4] MEIN L G, LARSON C L. Modeling infiltration during a steady rain[J]. Water Resources Research, 1973, 9(2): 384-394. [5] CHU S T. Infiltration during an unsteady rain[J]. Water Resources Research, 1978, 14(3): 461-466. [6] 韩同春, 马世国, 徐日庆. 强降雨条件下气压对滑坡延时效应研究[J]. 岩土力学, 2013(5): 1 360-1 366. [7] 李秀珍, 何思明. 基于Mein-Larson入渗模型的浅层降雨滑坡稳定性研究[J]. 灾害学, 2015(2): 16-20. [8] 范严伟, 赵文举, 王昱, 等. 夹砂层土壤Green-Ampt入渗模型的改进与验证[J]. 农业工程学报, 2015(5): 93-99. [9] CHO S E. Surficial stability analysis by the Green-Ampt infiltration model with bedrock boundary condition[J]. Journal of Korean Society of Hazard Mitigation, 2015, 15(1): 131-142. [10] 詹良通, 贾官伟, 陈云敏, 等. 考虑土体非饱和特性的无限长斜坡降雨入渗解析解[J]. 岩土工程学报, 2010, 32(8): 1 214-1 220. [11] LU N, GRIFFITHS D V. Profiles of Steady-state suction stress in unsaturated soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(10): 1 063-1 076. [12] 李宁, 许建聪. 无限长均质斜坡降雨入渗解析解[J]. 岩土工程学报, 2012, 34(12): 2 325-2 330. [13] FREDLUND D G, RAHARDIO H. 非饱和土土力学[M]. 陈仲颐, 等译. 北京: 中国建筑工业出版社, 1997. [14] 李 毅, 王全九, 邵明安, 等. Green-Ampt入渗模型及其应用[J]. 西北农林科技大学学报(自然科学版), 2007, 35(2): 225-230. [15] MOORE I D, EIGEL J D. Infiltration into two-layered soil profiles[J]. Transactions of the ASAE, 1981, 24 (6): 1 496-1 503. [16] RAWLS W J, BRAKENSIEK D L, MILLER N. Green-Ampt infiltration parameters from soils data[J]. Journal of Hydraulic Engineering, 2014, 109(1): 62-70. (责任编辑: 沈芸) On the basis of the traditional Green-Ampt infiltration model, the extended infiltration model considering the depths of water table is established. Four different types of soil textures are adopted to obtain the corresponding analytical solutions and numerical solutions. The results show that the error of the ponding time is only 0.274 h and the error of relatively accumulative infiltration is 3.204%, which show that the proposed model is quite reasonable. Take the sandy loam for example, we use the validated model to analyze how the depth of the water table affects the rainwater infiltrate into unsaturated soil, the analysis shows that the infiltration rate, cumulative infiltration and the ponding time are less susceptible to the depth of water table. However, with the duration of the rainfall increase, the depth of wetting front is influenced more obviously. rainfall infiltration; Green-Ampt model; water table; unsaturated soil; physical infiltration model TU42 A Arainfallinfiltrationphysicalmodelconsideringthedepthofwatertable DOU Hongqiang, JIANG Senhui (College of Environment and Resources, Fuzhou University , Fuzhou, Fujian 350116, China) 10.7631/issn.1000-2243.2017.04.0582 1000-2243(2017)04-0582-07 2016-03-10 豆红强(1987-), 讲师, 主要从事边坡稳定, 渗流理论等研究, douhq@fzu.edu.cn 国家自然科学基金资助项目(51178423); 福州大学科研启动基金资助项目(510164)
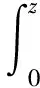
2 模型验证与分析



3 地下水位埋深对降雨的影响

4 结语

