页岩水力压裂数值分析

张 健，张国祥，李 良，马海春.

(1.中国华能集团清洁能源技术研究院有限公司，北京 102209；2.华能国际电力开发公司，北京 100031；3.合肥工业大学资源与环境工程学院，安徽合肥 230027 )

页岩水力压裂数值分析

张 健1，张国祥1，李 良2，马海春3.

(1.中国华能集团清洁能源技术研究院有限公司，北京 102209；2.华能国际电力开发公司，北京 100031；3.合肥工业大学资源与环境工程学院，安徽合肥 230027 )

利用abaqus软件对页岩水力压裂进行了数值分析建模，选用cohesive黏聚单元模拟裂纹的扩展过程。本文分析了裂纹发育过程中受到的水压变化过程，水压力在3个坐标轴方向随距离增加而减小；分析了不同压裂时刻页岩裂纹张开特征与注水点距离之间的关系，页岩裂纹的扩展与水压大小分布有一定的关系，但稳定的水力通道发育以后，裂纹基本稳定不变；对不同点水流速度随时间的变化情况进行了对比，水流速度在不同的位置对应时刻达到峰值，并且随距离增加，流速峰值变小；黏聚单元在水压作用下会发生破坏效果，给出了计算结束时对应的损伤程度，发现损伤破坏的扩展与水压大小关系密切，其分布范围代表了裂纹的发育程度。

页岩；水力压裂；黏聚单元；裂纹；水压；损伤

页岩是一种沉积岩，成分复杂，但都具有薄页状或薄片层状的节理，主要是由黏土沉积经压力和温度形成的岩石，其中混杂有石英、长石的碎屑以及其他化学物[1]。

随着计算机技术的发展，数值模拟已成为科学研究的重要手段之一，有关渗流—应力耦合机理研究、水力致裂耦合模型的建立及相关应用程序的开发都取得了一定的进展[2-3]。利用何种计算理论能够耦合实际情况中液、固相甚至气相的相互作用情况，得到裂纹发生、发展的过程，将是计算机仿真模拟水力压裂的重要研究内容。

文献[2-8]展示近些年来国内大学数值计算的一些成果，主要是利用有限元软件分析水力压裂的基本规律和影响因素，有些结论尚缺乏试验验证，如地应力的影响。本文利用abaqus数值计算软件，建立计算模型分析水平井水力压裂的过程，探寻水压的变化过程和分布，并探寻页岩水力压裂裂纹分布与水力通道的关系。

1 计算模型

取几何形状为一边长为30 cm的立方体作为分析对象，如图1所示，在一面中心处设立压裂液注入点，如图中的箭头所示。岩石采用弹性材料，中间建立cohesive黏聚单元，相关的单元参数见表1，其值大小由文献[4-10]得出。

其中，压裂液参数利用黏度参数控制，设置了3个方向的位移固定边界条件、初始地应力场地、孔隙度、水压力等条件，按照稳定流条件进行水力压裂，排量为0.067 m3/s，初始地应力是25 MPa(Z方向即垂直方向)，初始最大水平地应力为20 MPa(X方向)，初始最小水平地应力为15 MPa(Y方向)。黏聚单元选择了临界应力作为裂纹宽展准则，其计算公式为[11-12]：

(1)

σf——临界法向应力，MPa；

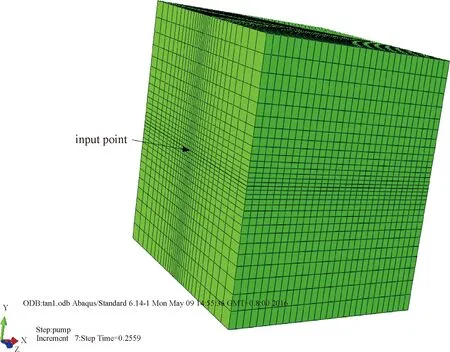
图1 分析模型Fig.1 Analysis model

参数页岩弹性模量/Pa页岩泊松比页岩渗透系数/(m·s-1)页岩孔隙度黏聚单元弹性参数/Pa黏聚单元破坏临界值/Pa压裂液黏滞系数/(mPa·s)数值4×10100.25×10-80.184×10102×106200

2 结果分析

2.1 裂纹扩展情况

随着注水的增加，在注水位置会产生高水压力，从而改变周边岩石黏聚单元的应力，达到上述的破裂准则后就会发生破裂。根据力学知识，裂纹应垂直最小主应力方向发育，如图2所示，在注水点位置裂纹开始产生，水压力分布在注水位置最高，随着距离的增加水压基本呈下降趋势，裂纹高度和长度随后在Z方向和X方向不断扩展，在Y方向裂纹宽度也随之增加。

2.2 水压变化情况

从注水点分别向X、Y和Z方向引3条观察路径，得到如图4所示的水压分布，从图中可以看出，水压随3个方向路径远离注水点而不断下降，其中X方向水压下降速度较慢，Y方向水压下降速度最快，Z方向水压下降速度居中。注入点的水压达到45 MPa，远离注水点后降到20～25 MPa。图5给出了不同观测点的水流速度变化曲线，其中，水流峰值不断往后退，说明各个点的破坏时刻对应的时间最早在注水点流速达到最大，此点的裂纹也是最大的宽度；随着距离注水点距离的增加，水流速峰值在较迟的时间达到，峰值大小也相对较小；在计算时间达到50 s以后，其曲线基本稳定不变，说明此时压裂已完成，形成稳定水流平衡状态。

图2 Y向位移图Fig.2 Displacement at Y-axis direction

图3 水压分布图(取1/2模型)Fig.3 Water pressure distribution (1/2 model)

图4 水压沿3个方向的变化Fig.4 Water pressure variations along three directions

图5 不同观测点水流速度变化Fig.5 Water velocity of different points

2.3 裂纹宽度分析

远离X方向注水点的位置，裂纹的宽度越来越小，图6显示不同的计算时间裂纹宽度的分布：计算时间为2s时，X=0的位置裂纹宽0.44 cm；随之X距离增大到2.7cm，裂纹宽度降到0；随后随计算时间的增加，X=0的位置裂纹在不断扩展，最宽达到0.86 cm，并且裂纹的前沿发育到更远的位置，可以达到X=19 cm。计算时间到了38 s后，裂纹变化不大，说明水力压裂后裂隙已产生稳定的水流通道，虽然不断稳定注水，但裂纹已经达到一个稳定流的状态。

2.4 黏聚单元损伤分布

对应的黏聚单元在受到注水压力的作用下，损伤单元从注水点位置也不断扩大。图7显示裂纹损伤发育的过程，红色代表损伤达到1，表示单元已经破坏，从而产生裂纹；损伤扩展到一定程度后，保持不再发展，这和裂纹的宽度不再发展是一致的。因此，页岩水压破裂是在水压作用不断扩展裂纹，直至稳定的水力通道形成后，裂纹将不再扩展；若要继续扩大裂纹，就需要更大的注水压力的支撑。

图6 不同时刻远离注水点距离对应的裂纹宽度Fig.6 Fracture width from the water input point at different times

图7 黏聚单元损伤分布Fig.7 Cohesive elements damage development

3 结论

(1)分析了计算条件下页岩中的水压力变化及分布，结合页岩中各观察点水流速度的变化情况，给出了水流速度峰值的分布；

(2)刻画了裂纹的张开度分布情况，结合黏聚单元的损伤破坏分布情况，探寻了裂纹发育与水压力之间的关系；

(3)页岩的水力压裂是流固耦合的复杂力学问题，其影响因素还有很多，要分析页岩的水力压裂效果还需开展更多的试验和数值计算分析。

[1] 张金川,金之均,袁明生.页岩气成藏机理和分布[J].天然气工业,2004,23(7):15-18.

[2] 陈勉，金衍，张广清.石油工程岩石力学[M].北京：科学出版社，1998：10-13.

[3] 胡永全，赵金洲，曾庆神，等.计算射孔井水力压裂破裂压力的有限元方法[J].天然气工业，2003，23(2)：58-60.

[4] 王瀚.水力压裂垂直裂缝形态及缝高控制数值模拟研究[D].合肥:中国科学技术大学, 2013.

[5] 张广明,刘合,张劲,等.储层流固耦合的数学模型和非线性有限元方程[J].岩土力学,2010,31(5):1657-1662.

[6] 彪仿俊.水力压裂水平裂缝扩展的数值模拟研究[D].合肥:中国科学技术大学,2011.

[7] 连志龙.水力压裂扩展的流固耦合数值模拟研究[D].合肥:中国科学技术大学,2007.

[8] 朱万成,唐春安,杨天鸿.岩石破裂过程分析(RFPA2D)系统的细观单元本构关系及验证[J]. 岩石力学与工程学报,2003,22(1):24-29.

[9] 何增军,王战丹,宋成立,等.利用数值模拟技术研究扶余油田周期注水模式[J].非常规油气,2016,3 (4):65-70.

[10] 熊文学,袁旭,惠涛,等.煤层气直井压裂参数优化设计[J].非常规油气,2016,3(4):95-103.

[11] 黄筑平.连续介质力学基础[M].北京:高等教育出版社,2003:298-328.

ShaleHydrofractureSimulationAnalysis

Zhang Jian1, Zhang Guoxiang1, Li liang2, Ma Haichun3

(1.HuanengCleanEnergyResearchInstituteCo.,Ltd.,Beijing102209,China; 2.HuanengInternationalPowerDevelopmentCo.,Beijing100031,China; 3.SchoolofResourcesandEnvironmentEngineering,HefeiUniversityofTechnology,Hefei,Anhui230027,China)

By using abaqus software, the simulation analysis model for shale hydrofracture has been established. Cohesive elements have been chosen to calculate the propagation of crack. The hydraulic water pressure variations have been analyzed and the regularity that the water pressure declines along the three axis directions has been suggested. The shale crack characteristics have been analyzed as the distances increase from the input point. The crack propagates in corresponding with the water pressure distribution. As steady water passage has been opened up, crack will be unchangeable. Water flow velocities at different points have been compared with. The flow velocity peak values at different points appear at different step time and decrease from the input point. The damage situation for cohesive elements have been studied associated with the water pressure and it represents the crack development degree.

shale; hydrofracture; cohesive elements; crack; water pressure; damage

TV131；O241

A

中国华能集团科技项目“重庆酉阳东区块储层压裂裂缝形态的主要影响因素研究”(CERI/TY-14-HJKO5)资助。

张健(1984—)，男，湖北随州人，硕士，现主要从事页岩气开发技术研究。邮箱：zhangjian@hnceri.com.