基于多项式曲线拟合的龙泉青瓷作品性态分析——以作品《有容乃大》为例

洪涛清，卢晓忠

（丽水学院 工学院，浙江丽水 323000）

基于多项式曲线拟合的龙泉青瓷作品性态分析
——以作品《有容乃大》为例

洪涛清，卢晓忠

（丽水学院 工学院，浙江丽水 323000）

基于数学与艺术相结合的理念，应用数学方法对青瓷作品《有容乃大》的造型设计进行理性分析。首先，运用计算机软件对作品进行数据提取；然后，通过曲线拟合给出曲线的多项式高次方程；最后，进行曲线的性态分析。拟以此来说明数学美在艺术设计中的重要应用。

龙泉青瓷；《有容乃大》；曲线拟合；性态分析

将艺术创作与科学理性分析相结合是近年艺术研究和工业生产的新方向。数学与艺术的最大关联，在于它们都需要人类的思维灵感和丰富的想象力[1]。艺术诠释了数学内涵，使数学变得通俗易懂；数学开拓了艺术蕴涵，开创了艺术的新方法，使艺术变得丰富多彩且意味深长。数学元素与龙泉青瓷协同创新研究就是试图将数学方法广泛应用于龙泉青瓷产品的艺术设计分析与研究。

《有容乃大》青瓷作品（如图1）是丽水学院张建平教授2016年的倾力之作，是丽水学院服务地方促进区域经济发展的成功范例，也是浙江省龙泉青瓷协同创新中心的标志性成果。我们选取《有容乃大》作为数学元素分析的案例，进行曲线化数据提取并用多项式拟合出方程。最后对曲线方程进行性态分析，发现数学美在艺术设计中的重要应用。

图1 《有容乃大》照片

图2 《有容乃大》数字结构图

1 数据的提取

《有容乃大》首批上市交易作品共120件，申购当天入金13亿人民币。在上市之前，我们从中挑选了目测最为完美的一件，先利用三维扫描技术做出瓶体的数字结构图，如图2。然后，进一步提取出轮廓线（瓶体的生成曲线）的相关尺寸，表1给出了拟合曲线取点坐标数据，我们将对这组数据进行数学分析。

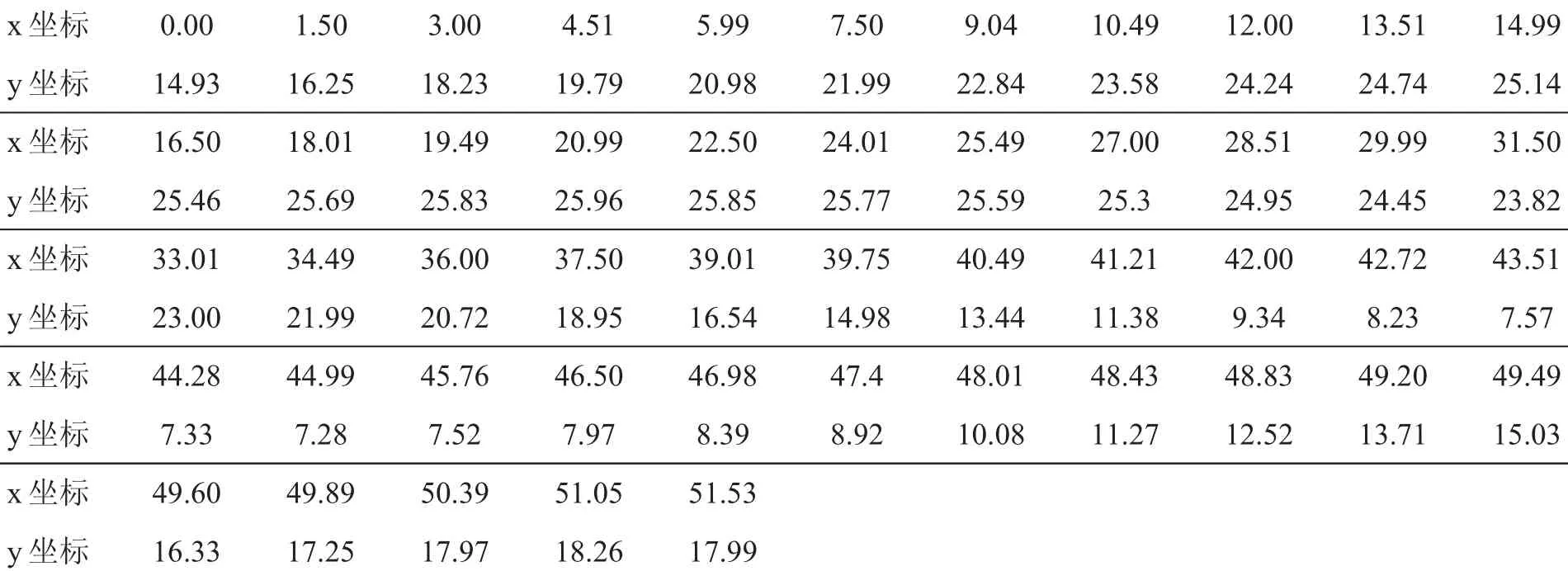
表1拟合曲线取点坐标表

利用上述数据，我们进行了共计26种函数类型的拟合。我们试图对整条曲线进行拟合，发现在瓶子颈部这里误差较大，故对曲线采取了分段拟合的策略。为便于在坐标系中处理，我们将数据缩小为原来的1/3并进行了转置处理，如图3所示。

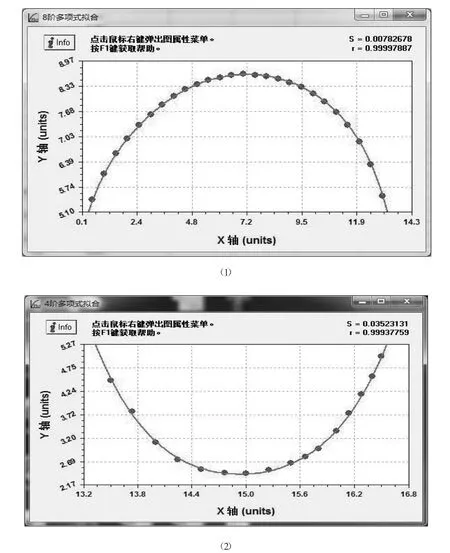
图3 拟合曲线取点图

拟合情况比较理想的方法有多项式拟合、Hoerl拟合等[2]，图4给出了最为理想的多项式拟合曲线的情况。我们在同一坐标系里绘出扫描结构图和上面拟合出的函数图像，曲线V2AE为8阶多项式图像，曲线EBV1为4阶多项式图像。

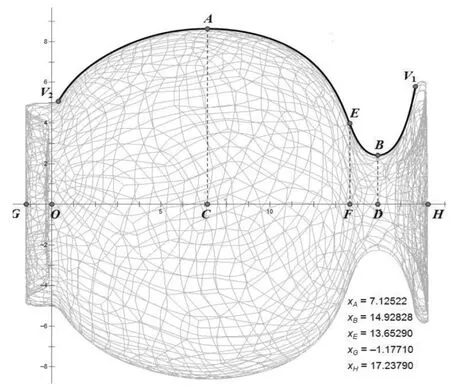
图4 拟合后的曲线图

可以直观地看出，拟合曲线和原瓶的轮廓线几乎完美吻合，分段曲线拟合比采用单一曲线拟合更为精确。表2给出上述拟合结果的多项式解析表达式。

表2 分段曲线的多项式拟合解析表达式

2 数据的分析

艺术的美往往来自于一种直觉，而通过数据分析可以让我们进一步明白这种美缘于何处。下面，我们对《有容乃大》青瓷作品的数据进行分析。

经计算，曲线V2AE的方程为f（x）=a+bx+cx2+dx3+…+ix8，曲线EBV1方程为g（x）=a0+b0x+c0x2+d0x3+e0x4，函数解析式中各系数参看表2。利用导数工具，易求得腰部最高点A和颈部最低点B（曲线极大值点和极小值点）的位置分别在xA=7.125 22和xB=14.828 28，瓶身和瓶颈的分界点E（曲线拐点）在xE=13.652 90。

2.1 曲线性态分析

2.1.1 连续性与光滑性分析

由于分段曲线都是多项式，而且在分界点E处有

所以，瓶体的生成曲线处处连续。其次，还有

可见，瓶体的生成曲线处处光滑。龙泉青瓷以其温润如玉的釉色而闻名天下[3]，光滑曲线与光滑曲面是这一特色的前提保障。

2.1.2 单调性与凹凸性分析

由f'（x）=0，g'（x）=0得极值点xA=7.125 22和xB=14.928 28，加之分段曲线分界点xE=13.652 90。通过计算，得

当x≤xA或x≥xB时，有f'（x）＞0，g'（x）＞0，曲线单调递增；

当xA≤xB≤xE或xE≤x≤xB时，有f'（x）＜0，g'（x）＜0，曲线单调递减；

当 x≤xE时，f"（x）＜0曲线呈现凸性；当 x≥xE时，g"（x）＜0 曲线呈现凹性。

显然，xE=13.652 90为曲线的拐点。正是因为曲线的单调性与凹凸性形成了《有容乃大》青瓷作品婀娜多姿的完美造型。

2.2 比例关系

另外，易求得下列比例关系：

腰最胖点近似于瓶体的黄金分割点附近，而黄金分割是美学中非常重要的一条原则。腰最胖点近似位于瓶身的中点，具有一种对称美。

理性的数据分析，让我们看到了《有容乃大》瓶身主体部分“大”得有理，美得自然。极大值点体现了容量大的特点，黄金分割点及对称性都体现了自然之美。通过数据分析，我们很好地诓释了《有容乃大》的文化特点。

2.3 曲率图像

我们进一步算出两条曲线的曲率函数，并绘制出其函数图像，如图5所示。不难看出，曲线V2AE的曲率变化非常小，近似为一水平直线，基本符合圆弧的特点，而曲线EBV1的曲率明显具有对称变化这一特点，基本符合抛物线的形态。圆弧线与抛物线成为了艺术家眼中所青睐的常用曲线。

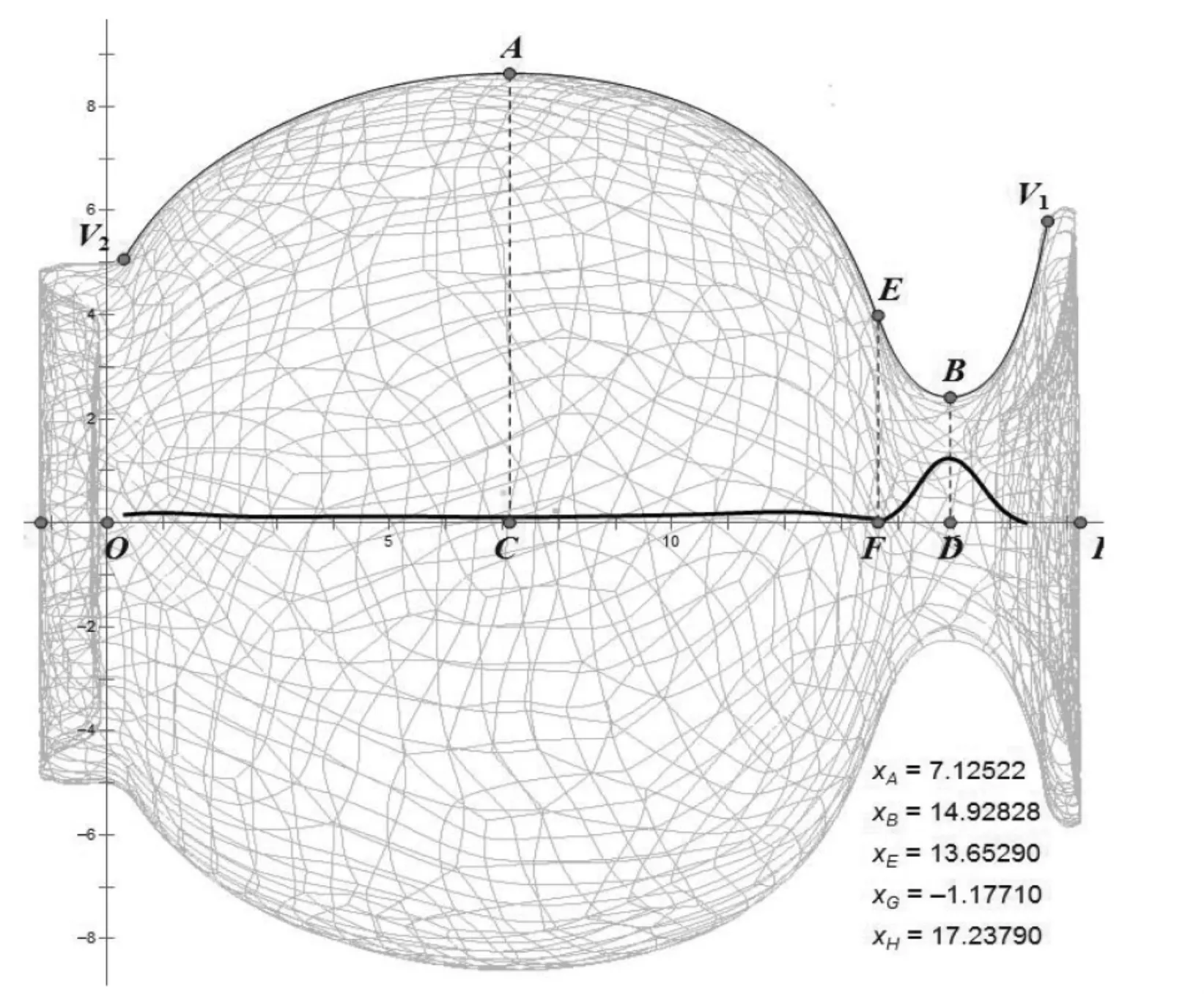
图5 拟合曲线的曲率图

3 结语

本文利用数学工具对龙泉青瓷作品《有容乃大》进行数据分析并发现美的初步研究，着重点在于曲线分析。后期将从曲面角度进一步分析，提出一些改进措施。根据改进的数据，我们拟利用3D打印技术来制作《新有容乃大》作品。

［1］袁震东，林磊.数学与艺术：无穷的碎片［M］.上海:上海教育出版社，2006：8.

［2］卢晓忠，洪涛清，吴新伟.从“玉壶春”看科学数据与艺术设计［J］.中国陶瓷（艺术版），2016（4）：149.

［3］张建平，李岩.近年来古代龙泉青瓷研究综述［J］.古陶瓷研究，2010（8）：74.

An Analysis on Curves of Works of Longquan Celadon Art Using Polynomial Curve Fitting Based on The Case of Yourongnaida

HONGTaoqing，LUXiaozhong
（FacultyofEngineering，Lishui University，Lishui 323000，Zhejiang）

Based on the principle of bounding mathematics and arts，this paper analyzes a work of Longquan celadon named Yourongnaida.First，we extract data through the computer software.Then we find out the higher order polynomial by curve fitting.Finally，we analyze its properties that illustrate the important applications of mathematical beauty in art design.

Longquan celadon；Yourongnaida；curve fitting；property analysis

10.3969/j.issn.2095-3801.2017.05.006

O182

A

2095-3801（2017）05-0036-06

2017-03-23；

2017-05-17

龙泉青瓷协同创新中心项目“数学元素与龙泉青瓷协同创新研究”（PY2016QCXT04）

洪涛清，女，浙江缙云人，副教授，硕士。