多道瞬态面波在复杂地形条件下岩层划分中的应用研究

席超强， 张平松， 李建宁， 丁美青

(安徽理工大学 地球与环境学院， 淮南 232001)

多道瞬态面波在复杂地形条件下岩层划分中的应用研究

席超强， 张平松， 李建宁， 丁美青

(安徽理工大学 地球与环境学院， 淮南 232001)

在复杂地表条件下，利用瑞雷面波进行勘探时，需要考虑地形对瑞雷波场传播地影响。针对倾斜地表两层地质模型，通过设计不同展布方向的检波器排列进行瑞雷波信号采集，利用高精度交错网格有限差分法，讨论经过快速傅里叶变换后的地震记录F-V频率谱，通过对比信号频率谱与理论多阶频散曲线，分析在不同地形条件下瑞雷波传播能量的变化特征，并提取叠加频散曲线；运用遗传算法对采集到的地震记录进行基阶与高阶瑞雷波联合反演得到目的层厚与初始模型层厚进行误差对比；并对理论正演初始模型的频散曲线与各地质模型利用F-K法提取的频散曲线进行全局拟合误差计算。分析表明：倾斜地形进行多道瞬态瑞雷面波勘探，相对于下部激发、上部激发会产生高阶频散趋势，因此对下部激发的地震记录进行反演产生的厚度误差相对较小。

瑞雷波； 倾斜； 地层划分； 联合反演

0 引言

近年来，瑞雷波在浅层地质勘查和环境调查方面地应用越来越广泛，然而在实际勘察工作中往往会遇到起伏的地形条件，在这种复杂的地形条件中采集到的瑞雷波具有不同的传播特征。为研究瑞雷波在层状介质中的频散特征，大量学者进行了深入的正演研究。从Haskell[1]提出计算瑞雷波频散曲线的Haskell算法开始，许多学者提出多种切实可行的频散曲线数值运算方法，Abo-Zena[2]通过反对称矩阵的循环运算得到瑞雷波频散方程；张碧星[3]采用柱坐标系研究瑞雷波频散问题，简化计算；凡友华[4]在柱坐标系下基于快速矢量传递矩阵提出快速矢量传递算法；潘佳铁[5]利用快速广义反射投射系数法计算瑞雷面波的群速度，并用数值实验的方法合成了两个典型模型的群速度频散曲线；袁腊梅[6]通过将广义反射-投射系数算法无量纲化得到瑞雷波频散函数的公式体系。

随着山区、滑坡等地形复杂地区地震勘探的兴起，大量专家学者基于弹性交错网格有限差分法，对起伏地形条件下的瑞雷波地震波场进行正演模拟。Hestholin等[7]对起伏地表下弹性波传播有限差分数值模拟进行研究；Robertsson[8]给出了含起伏地表弹性和粘弹性介质中地震波传播的有限差分模拟方法；张大洲[9]应用2×12阶高精度交错网格有限差分法,建立了震源位于自由表面时模拟瑞雷波的边界条件，对均匀半空间模型模拟；熊章强[10]模拟分析小凸起小凹陷模型条件下的瑞雷波场传播特征；江凡[11]模拟起伏地表条件下的瑞雷波全波场正演，通过坐标变换的方式实现起伏地表自由边界条件；琚长辉[12]进行了倾斜和塌陷地形的弹性波场交

错网格有限差分数值模拟。以上对瑞雷波在数值模拟上的分析主要集中在完善对瑞雷波有限差分模拟地实现与瑞雷波传播受地形影响方面，并未对地形、对瑞雷波频散特征影响进行分析。

研究瑞雷波面波在倾斜起伏地形条件下的传播特征和频散曲线，具有重要的现实意义，通过交错网格有限差分法，模拟倾斜地表下瑞雷波传播，并对地表凸起和凹陷以及平直地形模式进行波场模拟，在此基础上分析倾斜地形下瑞雷波频散特征，讨论“之”形特征，根据遗传算法对模拟得到的频散曲线进行反演，并与模型参数进行对比，获得了倾斜地形对岩土分层的影响。

1 数值模拟实验

根据倾斜地表的构造简化为双层介质模型，在模型表面进行瑞雷波数值模拟，通过频散特征对地层进行划分并与排列中点的层厚进行对比。我们设计四种双层均匀介质模型如图1所示，凹陷和凸起地形的宽度也是100 m，运用交错网格有限差分法使用弹性波动方程，模拟瑞雷波在模型中传播。模型的尺度为100 m×100 m，网格点数为1 000×1 000，模型介质参数为：上部地层用绿色表示，下部地层用蓝色表示。表1为两层倾斜地质模型的物性参数。

表1 两层倾斜地质模型参数

数值模拟使用的震源为主频20 Hz 的Ricker子波。如图1所示，每个模型从左到右依次有三个炮点，炮点1在模型上部激发，x=20 m处激发，26个检波器，道间距为2 m，检波器位置x=22 m～72 m；炮点3在模型下部激发，x=74 m处激发，26个检波器，道间距为2 m，检波器位置x=22 m～72 m。采样间隔为0.2 ms，采样长度为0.5 s。炮点2在模型中部x=47 m处激发，检波器沿地层垂直于炮点1、炮点3测线的方向展开，使用26个检波器，道间距为2 m。

平直、凸起、凹陷三种等厚表层模型的表层竖直深度均为10 m，在倾斜地表上部和下部进行震源激发；由于表层具有倾斜角度和起伏变化，排列中点相对于地层界面的距离不等于竖直方向深度。表2为四类模型三种激发方式排列中，点到沿垂直排列切线方向到地层分界面的距离。

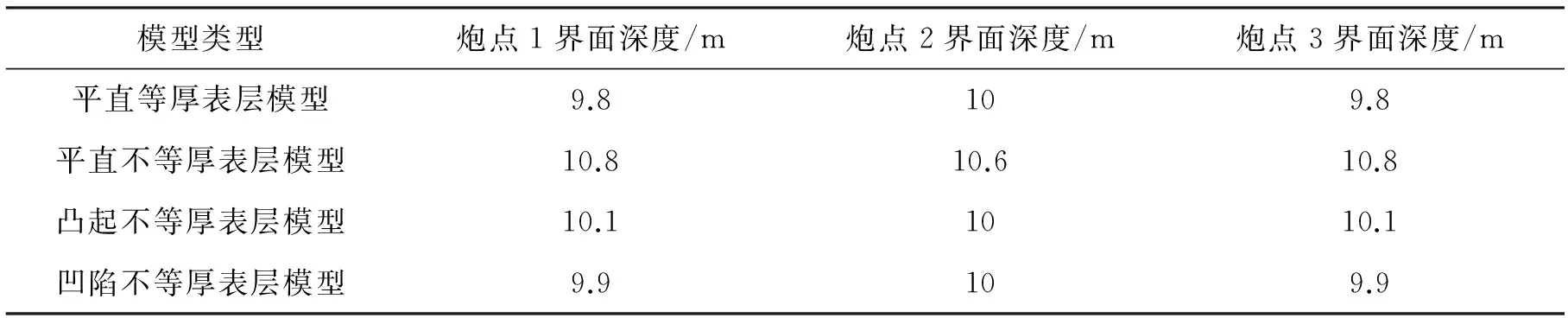
表2 两层倾斜地质模型参数

2 频散特征分析

2.1 频散谱分析

对高信噪比的瑞雷波地震记录采用有效的信号技术进行处理，实现瑞雷波地震波场分离提高频散曲线的提取精度和可靠性。目前主要的频散曲线提取算法有相移法、Prony法和拉冬变换算法等。笔者使用f-k域变换法对瑞雷波地震记录进行快速傅里叶变换，利用Vr=f/k的关系转换到f-v域进行频散曲线提取，可以实现多模式频散曲线的提取。

2.1.1 单倾直线等厚表层模型

从图2(a)可见，基阶波在低频占主导地位，在高频处于次要地位，在10 Hz～30 Hz频带范围内基阶波能量为主导，在35 Hz～45 Hz的频带范围内第二高阶能量为主导，45 Hz～60 Hz频带范围内第一高阶能量为主导。此时地震记录频散曲线为基阶面波与各高阶瑞雷波共同耦合作用的结果。拾取的瑞雷波会出现“之”字形拐点。

图2(b)频谱是根据震源为炮点2在检波点沿模型表面水平方向展开得到的模型模拟地震记录经过傅里叶变换得到。从图2(b)可见，在0 Hz～8 Hz的频带范围内，如图中箭头所示，相速度值急剧增加，与实际模型并不相符，因此在拾取频散曲线速度的时候在低频范围内需要谨慎，不得根据能量“脊”线盲目拾取，在8 Hz～30 Hz频带范围内，基阶能量占主导地位，在30 Hz～60 Hz，能量介于基阶能量和第一高阶能量之间，此时频散曲线应该是基阶波与第一高阶波相互叠加共同耦合的结果，此时叠加后的频散曲线也会出现“之”字形拐点。通过出现“之”字形拐点，与瑞雷波频散有关的参数有地层密度、地层厚度、纵横波速度、密度、泊松比。模型的两层地层的密度和泊松比均为0.45 g/cm3和1.8 g/cm3，说明利用“之”字形的这一特征可以为地层的速度分层提供参考依据。通过给定的频率和速度可计算得到确定的深度值，经计算发生拐点的深度为6.2 m，与实际模型的10 m并不相符，说明不能直接根据跳点处的深度，来确定岩性分层的深度，这与文献[13]关于“之”字形的描述相同。

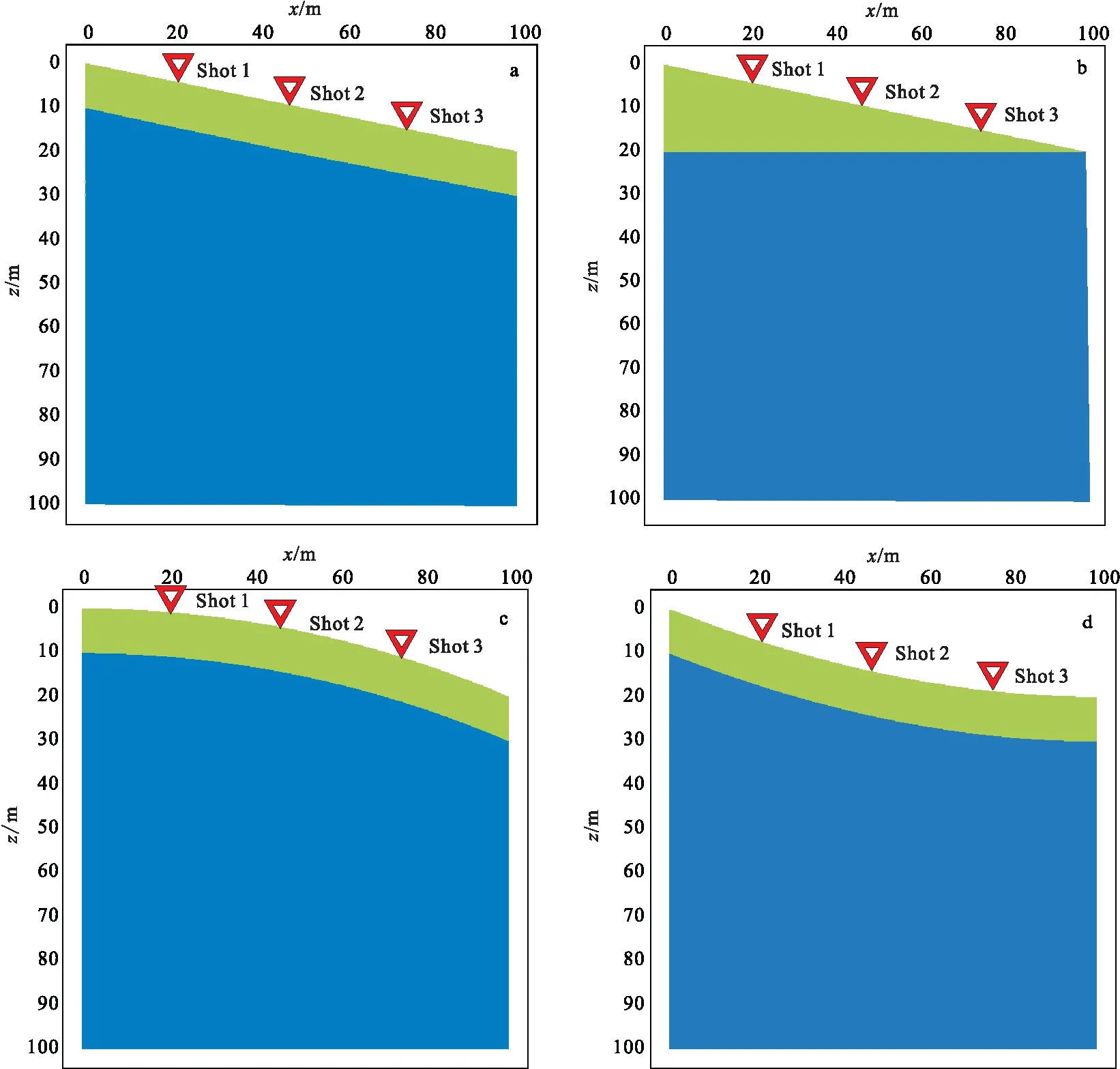
图1 两层倾斜地形模型Fig.1 Two inclined geological model(a)单倾平直等厚表层模型；(b)单倾平直不等厚表层模型;(c)单倾凸起等厚表层模型;(d)单倾凹陷等厚表层模型

图2 单倾直线等厚表层模型 瑞雷波F-V频率谱Fig.2 F-V Rayleigh wave frequency spectrum of pour equal thickness single linear surface model(a)炮点1频谱；(b)炮点2频谱；(c)炮点3频谱

从图2(c)可见，在8 Hz～30 Hz频带范围内，基阶能量占主导地位，在30 Hz～60 Hz，能量第一高阶能量占主导地位。

通过对比炮点1和炮点3位于模型表层上、下位置的频谱，上部激发的地震记录频散谱第二高阶能量分离较清晰；下部激发的地震记录频散谱清新分离第一高阶能量。炮点2频谱低频部分基阶能量主导，高频能量基阶能量和第一高阶共同耦合。

2.1.2 平直不等厚表层模型

从图3(a)可见，5 Hz～32 Hz频谱范围内能量主要属于基阶能量，30 Hz～60 Hz能量为第一高阶能量占主导地位。由图3(b)可见，排列为水平方向顺层激发，不受地形影响，在8 Hz～30 Hz频带范围内，能量主要属于基阶能量，在30 Hz～60 Hz，能量范围介于基阶能量和第一高阶能量之间，与前两组水平激发模型频谱规律相同。由图3(c)可见，在5 Hz～35 Hz频带范围内，基阶能量占主导地位，在30 Hz～60 Hz，能量第一高阶能量占主导地位，与第一组模型下部激发频散特征相同，45 Hz～50 Hz频带范围内面波能量受第一高阶和第二高阶能量共同耦合作用影响，有向第二高阶分离的趋势。

2.1.3 单倾凸起等厚表层模型

从图4(a)可见，8 Hz～26 Hz频谱范围内能量主要属于基阶能量，30 Hz～38 Hz能量为第一高阶和第二高阶共同耦合结果，38 Hz～51 Hz能量为第一高阶能量，与平直等厚模型频散特征相似，叠加频散曲线呈“基阶-第二高阶-第一高阶”的趋势。

从图4(b)可见，排列为水平方向顺层激发，不受地形影响，在8 Hz～30 Hz频带范围内，能量主要属于基阶能量，在30 Hz～60 Hz，能量范围介于基阶能量和第一高阶能量之间，与前两组水平激发模型频谱规律相同。

由图4(c)可见，在8 Hz～30 Hz频带范围内，基阶能量占主导地位，在30 Hz～60 Hz频带范围内，面波能量模式为第一高阶，未出现趋向第二高阶的特征，与第一组模型下部激发频散特征相同。

2.1.4 单倾凹陷等厚表层模型

从图5(a)可见，8 Hz～27 Hz和34 Hz～36 Hz频谱范围内能量主要属于基阶能量，28 Hz～32 Hz和35 Hz～47 Hz频谱范围能量为第一高阶能量，48 Hz～60 Hz能量为第二高阶能量，与平直等厚模型和凸起等厚模型频散特征不同，叠加频谱曲线呈“基阶-第一高阶-第二高阶”的趋势。

图3 单倾平直不等厚表层模型 瑞雷波F-V频率谱Fig.3 F-V Rayleigh wave frequency spectrum of pour straight single uniform thick surface model(a)炮点1频谱；(b)炮点2频谱；(c)炮点3频谱

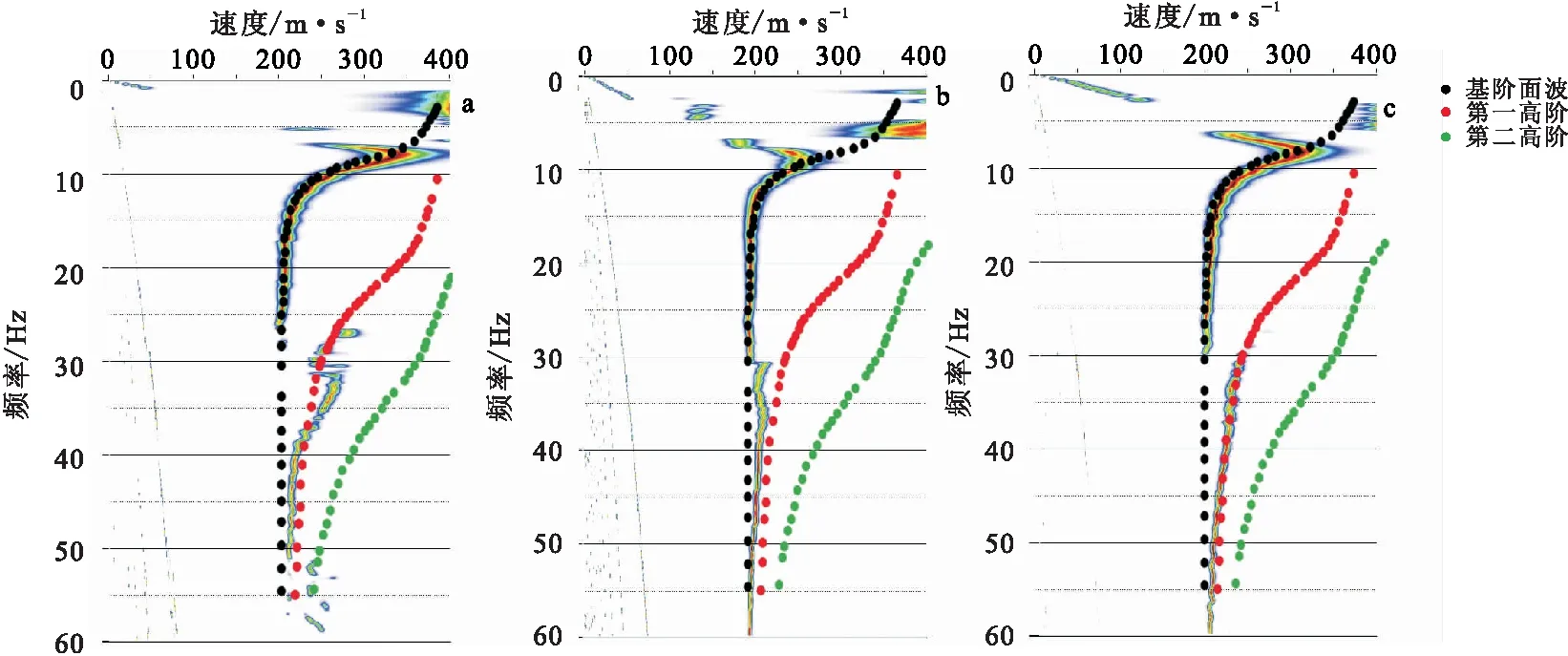
图4 单倾凸起等厚表层模型 瑞雷波F-V频率谱Fig.4 F-V Rayleigh wave frequency spectrum of single pour projections surface model(a)炮点1频谱；(b)炮点2频谱；(c)炮点3频谱

图5 单倾凹陷等厚表层模型 瑞雷波F-V频率谱Fig.5 F-V Rayleigh wave frequency of single pour depression surface model spectrum(a)炮点1频谱；(b)炮点2频谱；(c)炮点3频谱

从图5(b)可见，排列为水平方向顺层激发，不受地形影响。在8 Hz～30 Hz频带范围内，能量主要属于基阶能量，在30 Hz～60 Hz，能量范围介于基阶能量和第一高阶能量之间。与前三组水平激发模型频谱规律相同。基于有限差分的瑞雷波弹性波动方程数值模拟，在相同参数的运算结果较为稳定。

从图5(c)可见，在8 Hz～30 Hz频带范围内，基阶能量占主导地位，30 Hz～35 Hz面波能量呈现向第二高阶发育的趋势，在35 Hz～60 Hz频率范围内，第一高阶能量占主导地位。

通过对四个模型的频散曲线对比得到：①上部激发相对于下部激发和水平顺层激发方式更易发生高阶波；②在40 Hz以上的高频部分，模型中基阶波与高阶波的速度差异不大，判断频散的阶数需谨慎；③倾斜地形的凹陷凸起状态影响高频频带范围内高阶波的产生，凹陷地形，高频范围高阶波较发育。

2.2 频散拟合误差分析

根据模型的各层介质深度、纵横波速度、密度等参数，通过频散曲线正演公式计算可得到理论多模式频散曲线。由于在频散谱中部分高阶能量为两种模式波的共同耦合作用，通过手动定义前叠加频散曲线各部分的阶数，将叠加频散曲线与初始模型的各频带范围的多模正演曲线进行拟合误差运算。采用计算均方根误差的方法，来衡量叠加频散曲线与多模频谱的偏差。均方根值越小，表明全局相对拟合精度越高。

表3为4种模型各炮点所计算的叠加频散曲线与多模式理论频散曲线的均方根误差。

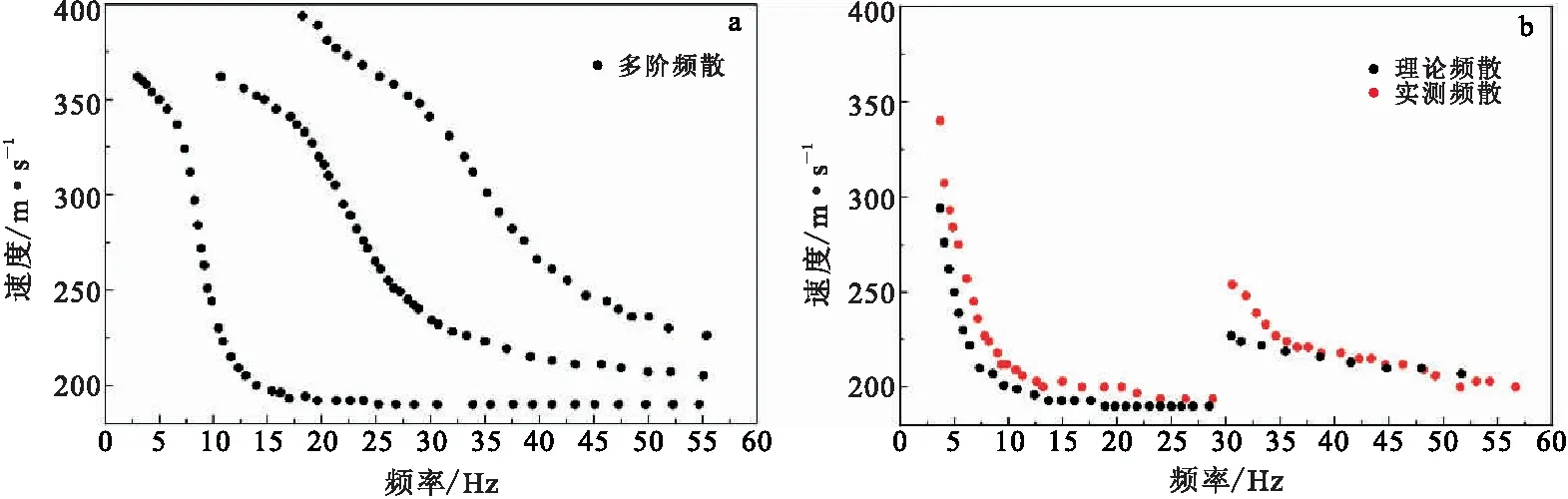
图6 理论多模频散与实测叠加频散Fig.6 Multi-mode dispersion theory and measured superimposed dispersion(a)10 m厚度表层的理论3阶频散；(b)模态分离的叠加频散与理论频散

模型类型炮点1均方根误差/%炮点2均方根误差/%炮点3均方根误差/%平直等厚表层模型7.23.604.10平直不等厚表层模型17.643.078.14凸起等厚表层模型9.053.844.42凹陷等厚表层模型9.693.776.22

通过对比模型各检波点排列均方根误差得到结论：①倾斜地形条件下，炮点3(下部激发)的数据记录提取的频散曲线与检波点排列范围中点的理论频散线的的拟合误差最小；②倾斜地形条件下，凸起地形的频散拟合误差小于凹陷地形。

3 层厚反演分析

本次建模使用四类简化的倾斜双层地质模型，使用沿地形倾向和顺层水平展布的三种检波器排列。多道瞬态瑞雷面波法对采集记录进行处理得到频散特征，视为得到所使用排列中心点深度范围内的频散特征，并根据频散曲线进行反演得到与横波速度有关的相应岩土体地质特征。

对叠加频散进行反演，建立初始模型，两层速度模型上层横波速度为200 m/s，下层横波速度为400 m/s，以地层深度为反演目标通过遗传算法运算，遗传算法反演参数：种群大小64，迭代次数30，交叉概率90%，变异概率2%，种子数80，指数拉伸函数，采用二进制编码，获得全局非线性最优解。表4为四种模型的不同激震位置的地震记录。

将反演深度与目标层深度的两者之间的差值与模型的界面深度做差值，计算各炮点反演深度值的绝对误差(表5)。

将反演深度与目标层深度的两者之间的差值与模型的界面深度做比值，计算各炮点反演深度值的相对误差(表6)。

图7为四种模型各采集排列方式发演深度与初始模型深度的对比图。

通过对比遗传算法的深度反演结果与模型实际参数的对比，得到以下结论：①倾斜地形条件下，下部激震的记录提取的频散曲线反演的深度相对于上部激震更接近初始模型；②等厚模型的反演深度比较，上部和下部激震方式的反演相对误差：平直地表>凸起地表>凹陷地表；③不等厚表层模型的上、下层激震的反演深度均小于初始模型表层深度。

表4 模型地层反演深度

表5 模型地层反演深度绝对误差

表6 模型地层反演深度相对误差

图7 模型反演层厚对比图Fig.7 Comparison of layer thickness model inversion(a)单倾平直等厚表层模型;(b)单倾平直不等厚表层模型;(c)单倾凸起等厚表层模型;(d)单倾凹陷等厚表层模型

4 结语

通过对四种双层均匀介质模型的数值模拟，讨论了倾斜地表条件下利用多道瞬态瑞雷面波法探测岩土体深度的应用效果，得到以下结论：

1)倾斜地表相对水平地表对瑞雷波的传播造成影响，在倾斜条件下激发产生的地震记录更易产生基阶-高阶波的分离。

2)起伏地形影响瑞雷波的传播，凸起地形下的勘探结果优于凹陷地形。

3)在倾斜地表模型的条件下，震源置于排列系统下方的深度勘探效果要优于上部激震方式，可能与上部产生第二高阶波的分离有关。

综上所述，在倾斜地表条件下，通过多道瞬态瑞雷面波采集的数据利用遗传算法基阶-高阶联合反演，可以获得反映实际深度的结果，反演深度相对模型表层存在一定的误差。

[1] HASKELL N A. The dispersion of surface waves on multi-layered media.[J]. Bulletin of the Seismological Society of America, 1953, 43(1):86-103.

[2] ABO-ZENA A. Dispersion function computations for unlimited frequency values[J]. Geophysical Journal International, 2007, 58(1):91-105.

[3] 张碧星, 兰从庆. 分层介质中面波的能量分布[J]. 声学学报:中文版, 1998(2):97-106.

ZHANG B X, LAN C Q. Energy distribution of surface waves in stratified media[J]. Acta Acustica,1998(2):97-106.(In Chinese)

[4] 凡友华, 刘家琦. 层状介质中瑞雷面波的频散研究[J]. 哈尔滨工业大学学报, 2001, 33(5):577-581.

FAN Y H, LIU J Q. Research on the dispersion of rayleigh waves in multilayered media[J]. Journal of Harbin Institute of Technology, 2001, 33(5):577-581. (In Chinese)

[5] 潘佳铁, 吴庆举, 李永华,等. 基于快速广义反射透射系数方法的面波群速度计算[J]. 地球物理学进展, 2009, 24(6):2030-2035.

PAN J T, WU Q J, LI Y H, et al.Group velocities computation of surface waves based on the fast generalized R/T coefficient method[J].Progress in Geophysics，2009, 24(6):2030-2035. (In Chinese)

[6] 袁腊梅, 凡友华, 孙书荣. 广义反射-透射系数算法的无量纲化[J]. 地震学报, 2009, 31(4):377-384.

YUAN L M, FAN Y H, SUN S R. Making the calculation of generalized reflection transmission coefficients dimensionless [J]. Acta Seismologica Sinica, 2009, 31(4):377-384. (In Chinese)

[7] HESTHOLM S, RUUD B. 2D finite-difference elastic wave modelling including surface topography 1[J]. Geophysical Prospecting, 1996, 42(5):371-390.

[8] ROBERTSSON J O A. A numerical free-surface condition for elastic finite-difference modeling in the presence of topography[J]. Geophysics, 1996, 61(6):1921-1934.

[9] 熊章强, 南坤, 唐圣松. 起伏地表二维瑞雷面波正演模拟及波场分析[J]. 物探化探计算技术, 2010, 32(5):470-475.

XIONG Z Q, NAN K, TANG S S.Forward modeling and wave field analysis of 2D Rayleigh wave based on irregular topography [J].Computing Techniques For Geophysical And Geochemical Exploration,2010, 32(5):470-475. (In Chinese)

[10] 江凡, 林智勇. 瑞雷波在滑动面探测中的应用效果讨论[J]. 福州大学学报:自然科学版, 2014, 42(2):299-304.

JIANG F, LIN Z Y. Discussion of the application effect of Rayleigh wave in the detection of sliding surface[J]. Journal of Fuzhou University( Natural Science Edition),2014, 42(2):299-304. (In Chinese)

[11] 张大洲, 熊章强, 顾汉明. 高精度瑞雷波有限差分数值模拟及波场分析[J]. 地球物理学进展, 2009, 24(4):1313-1319.

ZHANG D Z, XIONG Z Q, GU H M. Namerical modeling of Rayleigh wave using high-accuracy finite-difference method and wave field analysis[J].Progress In Geophysics, 2009, 24(4):1313-1319.(In Chinese)

[12] 琚长辉, 王伟, 王祥春,等. 基于起伏地形的瑞利面波有限差分数值模拟[J]. 东华理工大学学报:自然科学版, 2015, 38(3):319-324.

JU C H,WANG W,WANG X C, et al. Finite-difference numerical modeling of Rayleigh wave based on relief surface [J]. Journal of East China Institute of Technology, 2015, 38(3):319-324. (In Chinese)

[13] 刘雪明, 凡友华, 翟佳羽,等. 四种典型地层的瑞雷波“之”字型频散曲线数值模拟研究[J]. 地球物理学报, 2009, 52(12):3042-3050.

LIU X M,FAN Y H,ZHAI J Y, et al. Numerical simulation of Rayleigh wave zigzag dispersion curves of four typical strata[J].Chinese Journal Of Geophysics., 2009, 52(12):3042-3050. (In Chinese)

StratigraphicdivisioneffectofRayleighwaveexplorationintheinclinedundulation

XI Chaoqiang, ZHANG Pingsong, LI Jianling, DING Meiqin

(Anhui University of Science and Technology,Huainan 232001,China)

In the complex surface conditions, the use of Rayleigh wave exploration, the need to consider the terrain on Rayleigh wave propagation. In this paper, the Rayleigh wave signal acquisition is designed by arranging the geophone array in different directions, and the FV frequency spectrum of the seismic record after fast Fourier transform is discussed by using the high precision staggered-grid finite difference method. By comparing the signal frequency spectrum with the theoretical multi-order dispersion curve, the variation characteristics of Rayleigh wave propagation energy under different terrain conditions are analyzed, indicating that the superposition dispersion curve is extracted. The genetic algorithm is used to calculate the ground-wave inversion and the thickness of the initial model. And then the error curves of the dispersion curves of the initial model and FK method are used to calculate the global fitting error. The results show that the higher frequency dispersion of the upper excitation is observed in the multi - channel transient Rayleigh wave exploration. Therefore, the inversion of the seismic records of the lower excitation results in a relatively small thickness error.

Rayleigh wave; tilt; stratigraphic division; joint inversion

P 631.4

A

10.3969/j.issn.1001-1749.2017.05.14

2016-09-02 改回日期： 2016-11-21

席超强(1993-)，男，硕士，主要从事瑞雷面波数值模拟研究， E-mail：cichaoqiang626@163.com。

1001-1749(2017)05-0669-08