MATLAB/STK联合仿真方法研究及GUI设计
苗继松,邵琼玲,任 元,吕永申,王 琛
(装备学院 航天装备系,北京 101416 )
MATLAB/STK联合仿真方法研究及GUI设计
苗继松,邵琼玲,任 元,吕永申,王 琛
(装备学院 航天装备系,北京 101416 )
详细介绍了MATAB(矩阵实验室)与STK(卫星工具箱)软件互联的方法;STK提供了相应的二次开发接口,可供MATLAB等软件进行二次开发;利用MATLAB和STK软件组合搭建仿真环境,以某Walker星座的设计与优化算法为例,具体介绍了联合仿真步骤流程及GUI界面的设计方法,并综合考虑了卫星轨道、传感器以及卫星编队等相关参数对星座最优设计的影响;结果表明,利用MATLAB和STK组合仿真能够以图像及数据列表的形式方便直观的给出最优结果,通过联合仿真,较大程度上减小了MATLAB的编程工作量,同时通过GUI界面的设计,以可视化的形式对主体程序进行集成,只需输入参数,便可快速进行相应的轨道仿真与数据输出,避免了在进行卫星星座设计时需反复对STK参数进行调整的工作;在对卫星星座设计与运行轨道的问题分析中,MATLAB/STK联合仿真相较于使用单一软件进行问题分析而言,要更加便利、形象直观。
矩阵实验室;卫星工具箱;联合仿真;GUI界面设计;星座优化
0 引言
MATLAB是由“matrix”与“laboratory”组合的简写,意为矩阵实验室(矩阵工厂),其是由美国mathworks公司发布的主要面向科学计算与数值仿真、可视化以及交互式程序设计的高科技计算软件[1]。MATLAB的基本单元是矩阵,基本功能是能够进行矩阵计算、创建用户界面、绘制函数和数据曲线以及对其他编程语言的程序进行连接等,可广泛应用于控制设计、工程计算、信号检测、信号通讯、图像处理及金融建模设计与分析等领域。它将数据可视化以及非线性动态系统的建模与仿真等诸多强大功能集成于一个易使用的视窗环境中,为很多科学领域提供了一种较为全面的解决方案,并在较大程度上摒弃了传统的非交互式程序语言(如C、Fortran、C++、JAVA等)的编辑模式。MATLAB的指令写法与实际数学和工程中常用的形式十分相近,故对同样一件事情来说,相对于用C,FORTRAN等语言完成,用MATLAB来解算问题要简便许多。同时,MATLAB也对像Maple等软件的优点进行了吸收,使其成为一款功能强大的数学软件[2]。
卫星星座设计最常用的仿真软件是STK(卫星工具箱),其是一款由美国Analytical Graphics公司开发的在航天领域中一直处于领先地位的商品化分析软件[3]。它能够对航天任务周期的全过程提供支持,主要包括概念设计、需求分析、运行测试和任务发射等应用[4]。STK可以对航空航天和防御等任务进行支援,利用它可以快速分析复杂空间环境,并可获得易于理解的图表和文本形式的分析结果,从而方便确定最佳问题解决方案。STK不但具有强大的数据仿真功能,还具有功能性较强的三维可视化模块,可对三维模型进行编辑[5],从而可以为STK和其它附加模块提供逼真的三维视景显示。在STK中通过设定预设场景,并对卫星等模型进行添加,并设定对应参数,就能够对卫星运行的二维和三维视景进行仿真实现。目前,STK最高版本为11.0,并由之前的Satellite Tool Kit更名为Systems Tool Kit,体现了其功能由卫星等对象拓展到了整个系统。由于美国自7.0版本开始就对中国实行禁运,目前STK国内可购买到的最高商业版本是 6.0版本。
虽然STK有效解决了三维视景显示问题,但在卫星的运行过程中,如果需要对卫星的相应参数进行改变,就需要停止仿真,重新按照相应流程一步步设定相关参数,从而不能实现对整个视景系统进行自动且连续地运行仿真。本文结合MATLAB和STK两个软件各自的优点,利用STK提供MATLAB接口模块[6],通过使用MATLAB进行相关数据处理,并给STK发送相关的控制指令控制STK的运行,使仿真系统按照MATLAB预先设定的程序运行,从而大大增强了卫星视景仿真的灵活性和可操作性[7]。本文以实际应用为背景,结合某Walker星座的设计与优化问题,对其分析过程以及相应的编程和GUI界面设计给出了详细的阐述与说明。
1 STK与MATLAB的相关配置
在STK与MATLAB进行联合仿真分析之前,需要对相关的环境进行配置。具体的配置过程会因为STK与MATLAB不同的安装顺序而有所不同[8]。下面进行具体介绍:
1.1 MATLAB先安装,STK后安装
如果用户的计算机中先安装了MATLAB,然后才安装STK软件,则STK会自动地配置好相关的初始化文件。用户只需要对MATLAB进行一定的设置就可以了。具体步骤如下:
1)分别启动STK和MATLAB;
2)在MATLAB中运行M文件stkinit,由于是首次运行,MATLAB会要求用户设置STK的运行环境;
3)在弹出的“STK/MATLAB接口配置”对话框中,选择“继续”按钮;
4)在弹出的“浏览文件夹”对话框中,选择STK安装目录下的“MATLAB”文件夹,从而确定所需M文件的位置;
5)之后,MATLAB将会打开另一个“浏览文件夹”对话框,要求选择Mex文件位置,和步骤4)一样,在STK安装目录下选择“bin”文件夹,并单击确定;
6)在之后MATLAB询问是否更改默认MexConnect连接配置、STK/Connect模块的初始化文件、STK的默认主目录时,全部选择“否”便可;
到这里,先进行MATLAB安装后进行STK安装的STK/MATLAB联合仿真环境就配置成功了。
1.2 STK先安装,MATLAB后安装
如果计算机中先安装了STK,而后才安装MATLAB,则除了要在MATLAB中进行STK的运行设置外,还要再对一些初始化文件进行相关设置。对该情况下MATLAB/STK联合仿真环境进行配置的主要步骤是:将STK安装目录里的“MATLAB;ToolboxLocal”文件夹中的“agiCleanPath.m”、“agiInit.m”和“stkInit.m”文件复制到MATLAB安装目录下的“Toolbox;Local”文件夹中,其余步骤按照1.1节中的内容进行相应设置便可。
1.3 运行MATLAB/STK
在STK/MATLAB联合仿真环境配置成功后,有MATLAB主动和被动两种运行方式。
1)MATLAB主动方式:分别启动STK和MATLAB,在MATLAB中运行M文件stkinit,然后开始STK和MATLAB的协同工作。在该模式下能够充分利用MATLAB的各种辅助工具,便于进行相应的设计工作;
2)MATLAB被动方式:先启动STK,然后选择“工具”,打开STK的“选项”对话框后,选中里面的“MATLAB选项卡”,单击“连接”按钮,STK就会立即启动MATLAB引擎。在该模式下,这两个程序的运行效率可以显著提高。
2 问题提出与总体方案设计
在配置MATLAB/STK的连接环境完成后,便可进行下一步的MATLAB/STK联合仿真应用。下面以某一简单案例,详细介绍使用MATLAB/STK联合仿真方式对星座轨道参数进行优化设计的完整分析过程。
2.1 问题陈述与限定条件
1)问题陈述:在星座设计与优化中,设计18颗卫星的Walker星座,确定对北纬45°,经度为33°的地面站进行访问的最大、最小时间以及对应的具体轨道设计参数。
2)限定条件:卫星高度1 000 km;传感器视场角110°,固定指向天底;星座的RAAN spread为360°,相位因子为2;轨道面数在3~9之间,轨道倾角在35~55之间。
2.2 总体方案流程设计
1)MATLAB与STK接口互联并调试;
2)用MATLAB进行具体星座及载荷的设定与编程。包括场景设置与命名、卫星运行时间设定、星上相关载荷的设定、轨道坐标系及轨道根数的确定等[9];
3)联合仿真程序对应的GUI界面设计。通过MATLAB提供的可视化面向对象的用户界面开发环境进行GUI应用程序的创建。在GUI界面中通过输入相关仿真参数,便可对比不同轨道倾角、不同轨道面数时卫星访问地面站的时间,从而确定出最优设计参数,并通过GUI界面进行显示。总体的流程如图1所示。
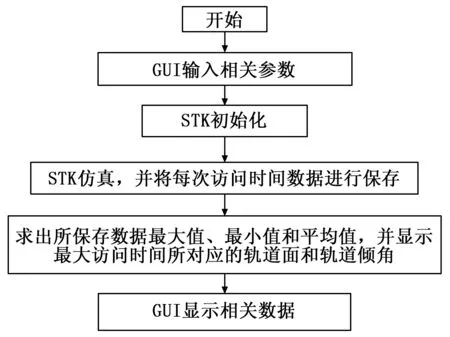
图1 MATLAB/STK联合仿真流程图
3 仿真程序设计
程序主要由两大部分组成:一个是主程序zhu.m(同时伴随一个GUI界面文件zhun.fig);另一个是运算程序hanshu.m。
主程序的主要功能是从GUI界面获取输入的参数,并将其传递给运算程序,经运算程序运算后,主程序将得到的返回参数用2D和3D图像显示,同时显示最终运算结果界面。最终结果包括在给定具体地面站的经纬度后,给出不同类型的Walker星座对该地面站最大访问时间、最小访问时间和平均访问时间,并同时给出访问时间最大时对应的Walker星座的轨道面数和轨道倾角。
由上述分析可知,运算程序是一个具有多输入多输出的功能函数。
3.1 主程序设计思路
主程序需要实现的功能是读取输入参数并传给运算程序,同时读取运算程序的返回参数并用界面显示。卫星的设计约束具体已知,由于卫星星座总星数为18颗,从而可以确定出设计变量中的轨道面数为3个具体值3、6、9。以上这些数据可以在程序中具体确定,但唯一不确定的是轨道倾角,因为轨道倾角只给出了范围,可能的数值有无穷多个,故这里还需要另外确定一个变量,这个变量就是步长,所以在GUI界面中,必须具有步长输入框。
为了及时方便得知计算的总次数以及程序在整个运算中具体到哪一步,可通过编程将该信息显示在MATLAB命令执行框中;同时为了实现将该程序生成计算机的可执行文件等后续工作,必须将STK初始化命令stkinit封装在主程序中[10];为了使MATLAB执行框中只显示关键信息,故需要用clc语句将在显示结果之前出现的内容进行清除,从而使界面显得更加干净整洁,使软件系统更加人性化。
3.2 运算程序设计思路
运算程序最先的工作就是从主程序中获取相应参数,然后进行场景创建、地面站创建、卫星创建、传感器创建、视场角参数设置、walker星座的创建以及链路和集群的创建等,之后进行仿真分析、存储相应数据并作图。将每次运算的访问时间结果存储在一个变量中构成结果矩阵,之后进行相应的结果处理。求取的最大访问时间、最小访问时间、平均访问时间,即为求取结果矩阵中的最大值、最小值和所有数据的平均值。根据最大值所对应结果矩阵中的行和列,即可判断出其所对应的轨道面数和轨道倾角的具体值,从而将这些参数返回给主程序进行显示。
根据问题描述,具体程序设计如下:
将程序的输入设为a(所需计算轨道倾角范围最小值)、b(所需计算轨道倾角范围最大值)、c(计算轨道倾角的步长)、d(地面站经度)、f(地面站纬度)5个变量。根据轨道平面的不同和轨道倾角的不同进行两层嵌套循环。在每次循环中,需要进行相应内容的创建:首先,创建一个场景,并设置场景时间(起始时间和结束时间,这里设为1天);而后创建一个地面站和一颗种子卫星,并在卫星上装载一个传感器,并设置传感器参数,定义传感器为简单锥角,锥角为55°,指向天底;然后设置卫星轨道参数,设置半长轴为7 278 km,偏心率为0,近地点幅角为0,平近点角为0。由于设置的时间为24 h,即86 400 s,故访问时间最大不超过86 400 s。在每次循环中,分别对种子卫星,星座类型,轨道平面数,每个平面卫星数,相位因子进行设置,并建立walker星座。而后建立一个星座集合并命名,建立一个传感器集合并命名为family2,建立一个连接于传感器集合和地面站之间的链路并进行命名。通过函数stkReport返回访问时间并形成矩阵,将矩阵命名为Total。计算并输出最大访问时间h,最小访问时间l,平均访问时间e。最后建立轨道平面,并将最终得到的轨道倾角和访问时间用2D和3D的图形展现出来。
4 MATLAB连接STK并进行计算的部分关键程序说明
在完成MATLAB与STK的连接后,便可在MATLAB中通过编程自行完成对STK中相应场景、地面站等对象内容的创建以及各个对象相应参数的设置和计算等。根据实际问题的需要,相应的MATLAB对STK的控制语句可以使用STK软件中的Help进行查询。依照本问题所需内容,在STK中查询相应语句如下:
1) 在stk中创建一个场景,命名为home,程序语句为stkNewObj('/','Scenario','home')。
2) 设置场景时间,起始时间为19 June 2016,结束时间为20 June 2016,程序语句为stkSetTimePeriod('19 June 2016 00:00:00.0','20June 2016 00:00:00.0','GREGUTC')。
3) 在stk中建立一个地面站,命名为target,程序语句为stkNewObj('*/','Facility','target')。
4) 根据输入的经纬度设置地面站位置,程序语句为stkSetFacPosLLA('Scenario/Lch/Facility/target', [latitude*pi/180; longitude*pi/180; 0])。
5) 在stk中建立一个卫星,命名为body,程序语句为stkNewObj('*/','Satellite','body')。
6) 在卫星body上装载一个传感器,命名为eye,程序语句为stkConnect(conid,'New','/ */Satellite/body/Sensor','eye')。
7) 定义传感器:简单锥角,锥角55度,程序语句为stkConnect(conid,'Define','*/Satellite/body/Sensor/eye','SimpleCone 55')。
8) 定义传感器的位置,程序语句为stkExec(conid,'Location */Satellite/body/Sensor/eye Center')。
9) 创建walker星座,并创建集群命名为family,程序语句为cs=['Walker ' ' */Satellite/body ' ' Delta ' aa ' ' bb ' ' cc ' ' dd ' Yes ConstellationName family']
10) 建立传感器集群,命名为family2,程序语句为stkConnect(conid,'New','/ */Constellation',' family2')
11) 建立传感器集群和地面站之间的链路,程序语句为stkConnect(conid,'New','/ */Chain',' relation'),stkConnect(conid,'Chains','*/Chain/relation','Add */Facility/target'),stkConnect(conid,'Chains','*/Chain/relation','Add */Constellation/family2')
12) 读取stk中报告时间,程序语句为[secdata,secNames]=stkReport('*/Chain/relation','Complete Chain Access')
5 仿真结果分析
5.1 仿真过程与图像
确定地面站的经度为33°,纬度为45°,GUI界面输入及仿真结果如图2~图7所示。
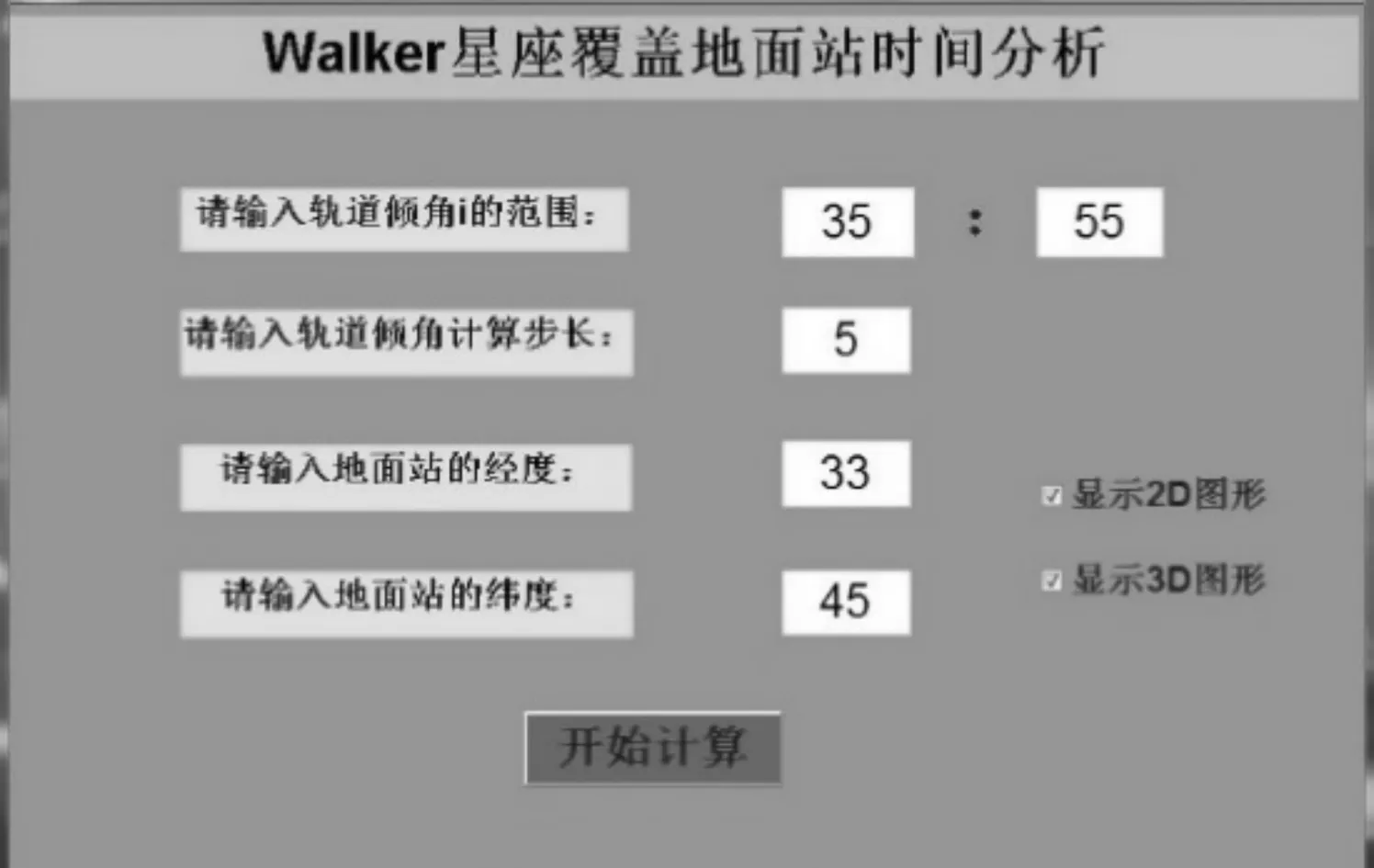
图2 GUI输入参数图
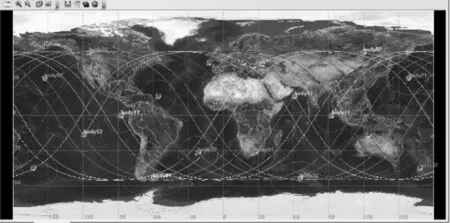
图3 18颗卫星的Walker星座二维图
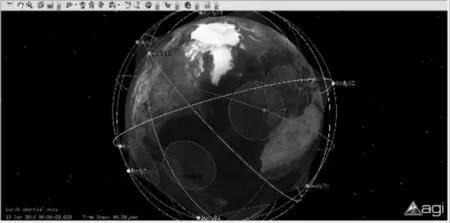
图4 18颗卫星的Walker星座三维图
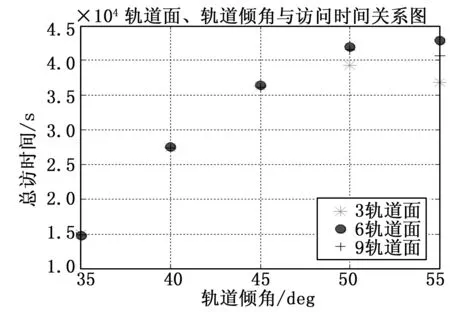
图5 轨道面、轨道倾角与访问时间关系图
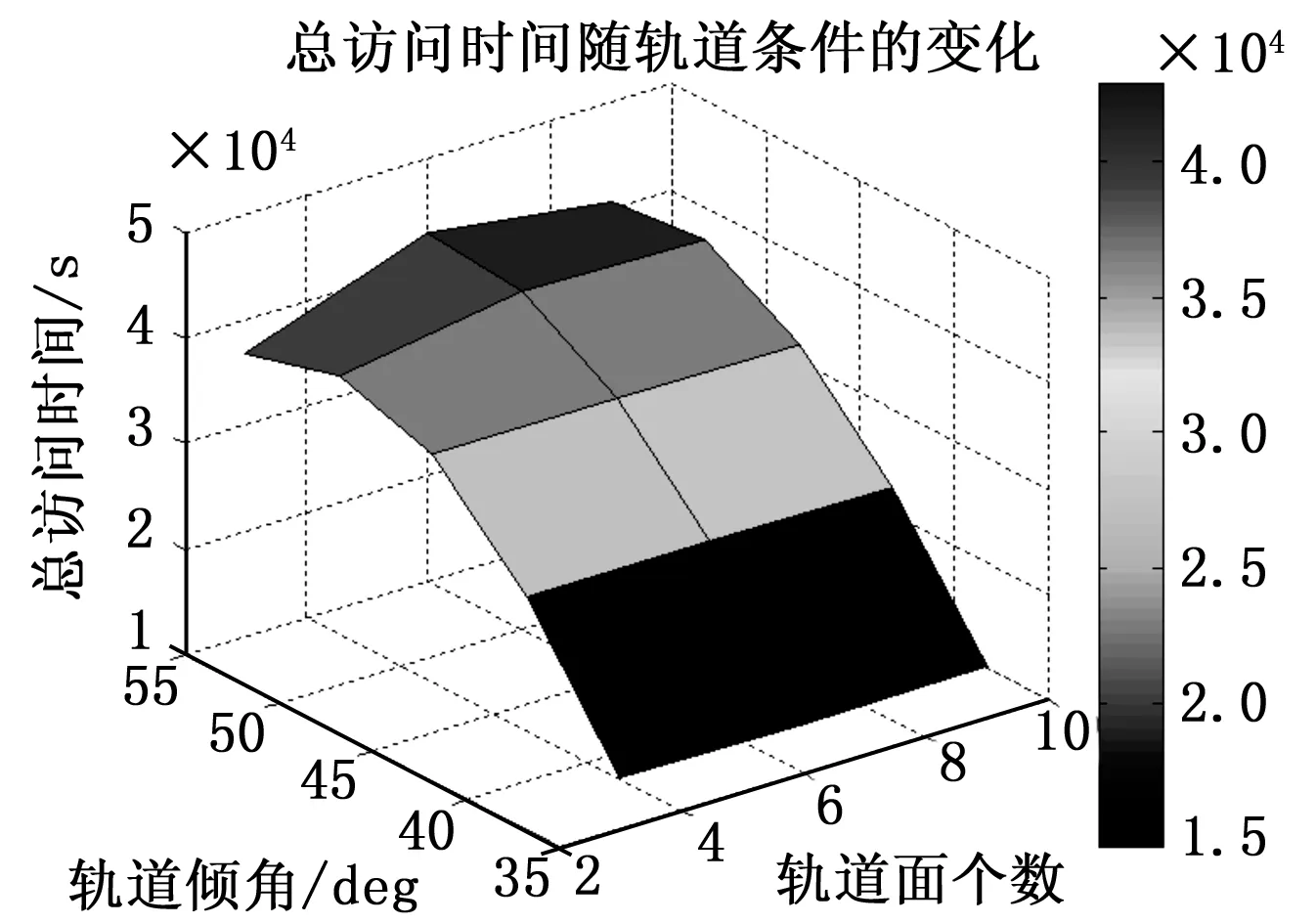
图6 总访问时间随轨道条件变化的3D图
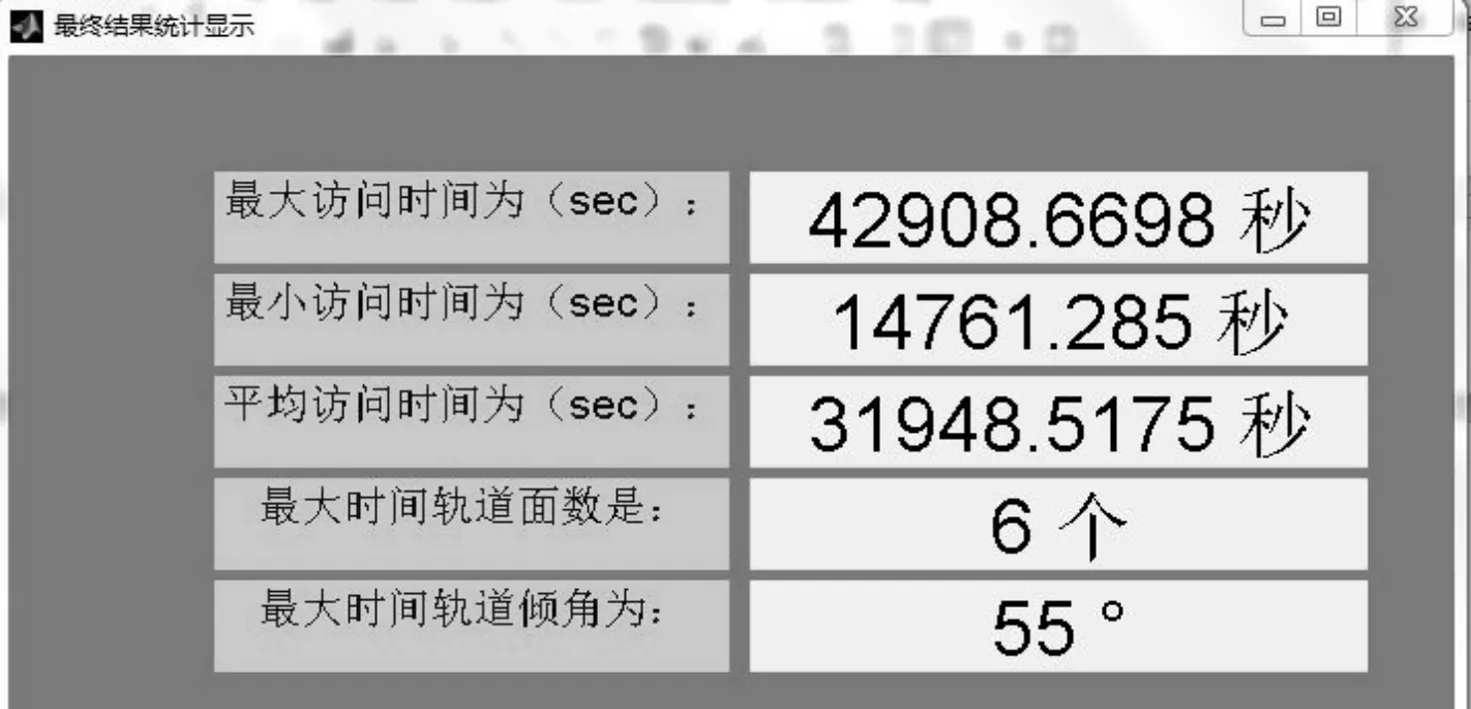
图7 最终结果GUI显示图
5.2 仿真结果分析
在图2的GUI界面中,依照1.1节中的相应问题和限定条件,输入轨道倾角的范围在35~55°之间,由于在这个范围之间,轨道倾角会有无数种选择,为了节省运算时间,同时又不失规律性,故综合考虑选择了轨道倾角的计算步长为5,即选择5组轨道倾角进行计算分析。输入地面站的经纬度,同时勾选2D和3D显示效果图,点击“开始计算按钮”,便会得到相应的仿真结果,如图2~图7所示。
由图5分析可得:在轨道倾角为35°,40°,45°时,轨道倾角不变,3轨道面、6轨道面和9轨道面时,由该18颗卫星组成的walker星座对经纬度为33°,45°的地面站在2016年6月19日~2016年6月20日这一天中的访问总时间相差不大;当轨道倾角为50°时,当walker星座为3轨道面时总访问时间最小,6轨道面比9轨道面时对应的总访问时间多,但相差不大;当轨道倾角为55°时,3种轨道面对应的总访问时间相差较大,且总访问时间由小到大依次为3轨道面、9轨道面和6轨道面。
此外,观察图5可进一步发现,在轨道倾角为35~55°时,随着轨道倾角的增加,walker星座的总访问时间整体上呈现增加的趋势。具体观察还可发现,除了6轨道面外,3轨道面和9轨道面在轨道倾角为55°时所对应的总访问时间达到最大,之后呈现随着轨道倾角的增加总访问时间下降的趋势。
由图5、图6的含义相同,只是将图5的内容以三维坐标的形式进行展现,更加直观。
图7给出了最终的计算结果。在5种轨道倾角以及3种轨道面的共15种组合情况下,给出了最大访问时间、最小访问时间以及15种情况的平均访问时间。同时也给出了总访问时间最大时对应的轨道倾角和轨道面数。
如果需要变换地面站的位置以及增加或减少计算时的轨道倾角个数,可以再开始的GUI界面中进行相关参数的调整即可。
5 结论
通过实际的应用案例,表明了MATLAB与STK联合仿真的优越性,在对多颗卫星组成的星座或单颗卫星进行仿真分析中,单纯借助MATLAB或STK某一种工具进行连续仿真分析时,会出现许多困难,具有诸多不便之处:若仅使用MATLAB进行仿真时,会出现编程工作量巨大的缺点;而只通过STK进行仿真时,会造成操作步骤繁琐等现实问题的出现。如果通过MATLAB和STK进行联合仿真,便可以极大地提高仿真效率。最后通过GUI界面的设计,使得MATLAB/STK仿真更加具有适用性。上述介绍的具体设计方法可以根据实际情况拓展至其他相应的仿真领域,具有较强的适用性。
[1] 刘 浩.MATLAB R2016a完全自学一本通[M].北京:电子工业出版社,2016.
[2] 张志涌,杨祖樱.MATLAB教程[M].北京:北京航空航天大学出版社,2015.
[3] 王 欣,金 虎. 基于STK/MATLAB的通信卫星场景建模[J]. 电子测试,2009(04):1-5.
[4] 刘夫成,刘朝晖,刘 文,等. 基于STK/matlab的空间目标序列星图仿真[J]. 红外与激光工程,2014(9):3157-3161.
[5] 杜玉萍. 基于STK/Matlab的航天器可见性仿真分析[J]. 光电技术应用,2014(6):80-83.
[6] 王 倩,王祖林,何善宝,等. 动态星间链路分析及其STK/Matlab实现[J]. 电讯技术,2010(9):19-23.
[7] 李 博,叶 晖,张宏伟,等. 基于STK/Matlab接口的卫星通信链路研究[J]. 无线电通信技术,2016(6):37-40.
[8] 陈宏宇,吴会英,周美江,等. 微小卫星轨道工程应用与STK仿真[M].北京:科学出版社,2016.
[9] 许丞梁,郭福成,刘 洋. 基于Matlab/STK的航天电子侦察效能仿真技术研究[J]. 航天电子对抗,2015(3):17-20.
[10] 李雅琼,李 杨,关贵注,等. MATLAB与STK组合仿真在星载天线伺服系统设计中的应用[J]. 遥测遥控,2016(5):1-5.
MATLAB/STK Joint Simulation Method and GUI Design
Miao Jisong,Shao Qiongling, Ren Yuan, Lü Yongshen, Wang Chen
(Academy of Equipment, Beijing 101416, China )
This paper introduces the method of MATLAB (Matrix Laboratory) and STK (Satellite Tool Kit) software interconnection. STK provides MATLAB the corresponding interface for further development. Using MATLAB and STK software to build simulation environment, the algorithm design and optimization of a constellation of Walker as an example, introduces the steps of the joint simulation process and the design method of GUI interface, and considering the influence of the satellite orbit, sensor, satellite formation and other related parameters on the optimal design of constellation. The results show that the combination of MATLAB and STK can be used to obtain the optimal results in the form of image and data list. The workload of MATLAB programming were greatly reduced by joint simulation. The corresponding track simulation and the data output can be completed when it comes to input parameters. It avoids the need to repeatedly adjust the STK parameters in the design of satellite constellation. In the analysis of the design of the satellite constellation, the MATLAB/STK joint simulation is more convenient and intuitive than a single software.
MATLAB; STK; adaptive; joint simulation; GUI design; constellation optimization
2017-02-21;
2017-03-11。
国家863项目(2015AA7026083)。
苗继松(1993-),男,河南焦作人,硕士研究生,主要从事航天器轨道设计与应用方向的研究。邵琼玲(1964-),男,北京市人,副教授,硕士研究生导师,主要从事航天器应用技术方向的研究
1671-4598(2017)08-0199-04
10.16526/j.cnki.11-4762/tp.2017.08.051
TP273
A

