改进蚁群算法的局部信息动态路径规划
赵 峰,杨春曦,陈 飞,黄凌云,谈 诚
(1.昆明理工大学 化学工程学院, 昆明 650500; 2.昆明理工大学 国土资源工程学院, 昆明 650093)
改进蚁群算法的局部信息动态路径规划
赵 峰1,杨春曦1,陈 飞1,黄凌云2,谈 诚2
(1.昆明理工大学 化学工程学院, 昆明 650500; 2.昆明理工大学 国土资源工程学院, 昆明 650093)
针对传统蚁群算法收敛速度慢、对动态路径变化适应性低的局限性,提出了一种基于局部信息获取策略的动态改进型蚁群算法。该算法利用局部信息获取策略,进行最优局部目标点的获取,然后调用改进蚁群算法获取局部区域内的最优路径,再重复循环获取新的最优局部目标点,直到找到全局目标点;与此同时,将提出的改进型蚁群算法应用于动态路径规划中的路径寻优与避障,仿真结果表明:提出的算法在具有与传统蚁群算法相当的路径优化效果的同时,能够有效适应障碍变化、大大提高了路径规划的收敛速度。
蚁群算法;局部信息;局部目标点;动态路径规划
0 引言
路径规划是移动机器人研究领域的一个重要分支[1-3],它研究的宗旨就是在有障碍物的路径中,在能够有效避免障碍物的前提下,寻找一条从给定起始点到给定终止点的最优的路径。其中最优指标既可以是距离最短,又可以是时间最短,还可以是带有权值的二者的结合,而障碍物可以分为静态障碍物和动态障碍物。因此,开展对该领域的研究对于科学实验、救援抢险、防爆、排雷等工程实施均具有重要意义[4].由于最优路径问题计算复杂度高,使得传统算法在面对规模较大、实时性较强的问题时,搜索效率较差[5]。而蚁群算法与其他启发式算法相比,在求解性能上具有很强的鲁棒性和计算复杂度低等特点。因此,该算法被广泛应用于解决旅行商[6-7]、车间调度[8-9]等问题的研究。
1 问题描述
由于采用传统蚁群算法(Traditional Ant Colony Algorithm,T-ACA)对静态障碍物问题的研究相对成熟,因此,人们在使用T-ACA进行路径寻优取得了一定效果。但T-ACA也存在一定的局限性,比如T-ACA会在机器人出发前设置几十只甚至上百只蚂蚁用来搜索最优路径,而且在此基础上还要进行迭代几十次甚至上百次,这样要花费大量的时间和计算资源。在路径寻优完成后,机器人将沿着搜寻到的一条最优路径行走。如果路径中的障碍情况发生变化,则原来搜寻到的最优路径就已经过时,还要再重新进行路径寻优。在这种情况下既没能够避开动态障碍,也浪费了时间。针对T-ACA在此方面的缺陷,国内外各方面的研究学者进行了相应的动态路径规划方面的探索。
2 相关工作
文献[10]从T-ACA中得到启发,限制信息素的上下限,在动态路径规划过程中,对动态障碍物进行了膨化处理,通过减小相应的膨化区域,进一步检测碰撞是否发生最终获取无碰最优路径。文献[11]引入人工势场的概念,为目标点定义吸引势能,障碍物定义排斥势能,机器人在势能的引导下可以从起点出发,避开障碍物,达到目标点。仿真结果表明,其算法能够适用于动态路径规划。文献[12]借鉴狼群分配原则,即:剔除掉最差路径上蚂蚁释放的信息素。仿真结果结果表明了该方法的可行性和有效性。
文献[13]的核心思想在于如何求得移动障碍物的线性函数,进而避开移动障碍物。仿真结果表明,该算法具有高实时性,而且非常适合在复杂和动态环境实时导航。文献[14]针对车辆路径规划问题,将A*算法与T-ACA相结合,并且对在蚂蚁走进“死胡同”到走出死胡同这条局部路径上不释放信息素,降低了其他蚂蚁走进“死胡同”的概率。仿真结果表明,改进算法不仅具有很好躲避动态障碍的能力,而且具有较短的寻优时间。
上述与T-ACA算法相关的研究,虽然取得了一定的效果,但是都采用了二次规划的思想,即:首先进行一次静态规划,再进行一次动态规划,虽然在避障效果方面有了大幅提高,但与此同时,计算复杂度和寻优时间也成比例的提高,而且也没有以某个具体的环境背景为参考变量。因此,本文,以城市某个区域内交通环境为切入点,侧重于整个区域内的各个路口的交通实时状态更新与规划,将交通环境简化为栅格地图的形式,路口的拥堵状况简化为各个栅格变换状况,并假设各个路口的交通只会在拥堵和畅通两个状态之间切换,不需要考虑各种如速度、加速度等运动状态变化状况,提出了一种改进蚁群算法的局部信息动态路径规划算法 (Local Information Dynamic Path Planning Based on Improved Ant Colony Algorithm,LD-ACA),该算法采用边走边规划的方式能够充分利用局部信息动态规划行走路径,具有良好的动态环境适应性和较低的计算复杂度。
3 LD-ACA实施步骤
3.1 基本定义
记G为机器人在二维平面内的运动区域,机器人映射实际交通环境中具体某个车辆,运动区域映射实际的交通规划区域,区域内的栅格编号如图1所示,在G中建立直角坐标系,以G左下角为坐标零点,横轴为X轴,纵轴为Y轴。设在相关区域内存在若干个障碍物栅格,在图1中用黑色栅格表示,实际交通环境中表示为路口拥堵。无障碍物栅格用白色栅格表示,实际交通环境中表示为路口畅通。其中每个栅格为正方形,其边长已知。假设机器人能够从起始点经过路径规划最终达到目的地点。机器人只在各个栅格内的中心点行走,关系计算公式如下:
X:xi=a·(mod(i,MM)-0.5)
(1)
(2)
关系式中,a为每个栅格的边长,横(纵)坐标的最大栅格数值为MM,栅格总数为e=MM·MM,每个栅格的坐标为(xi,yi),i为每个小正方形的栅格编号,mod为求余运算,而ceil为舍余取整运算。其中机器人的起始点和最终目的地点已知。
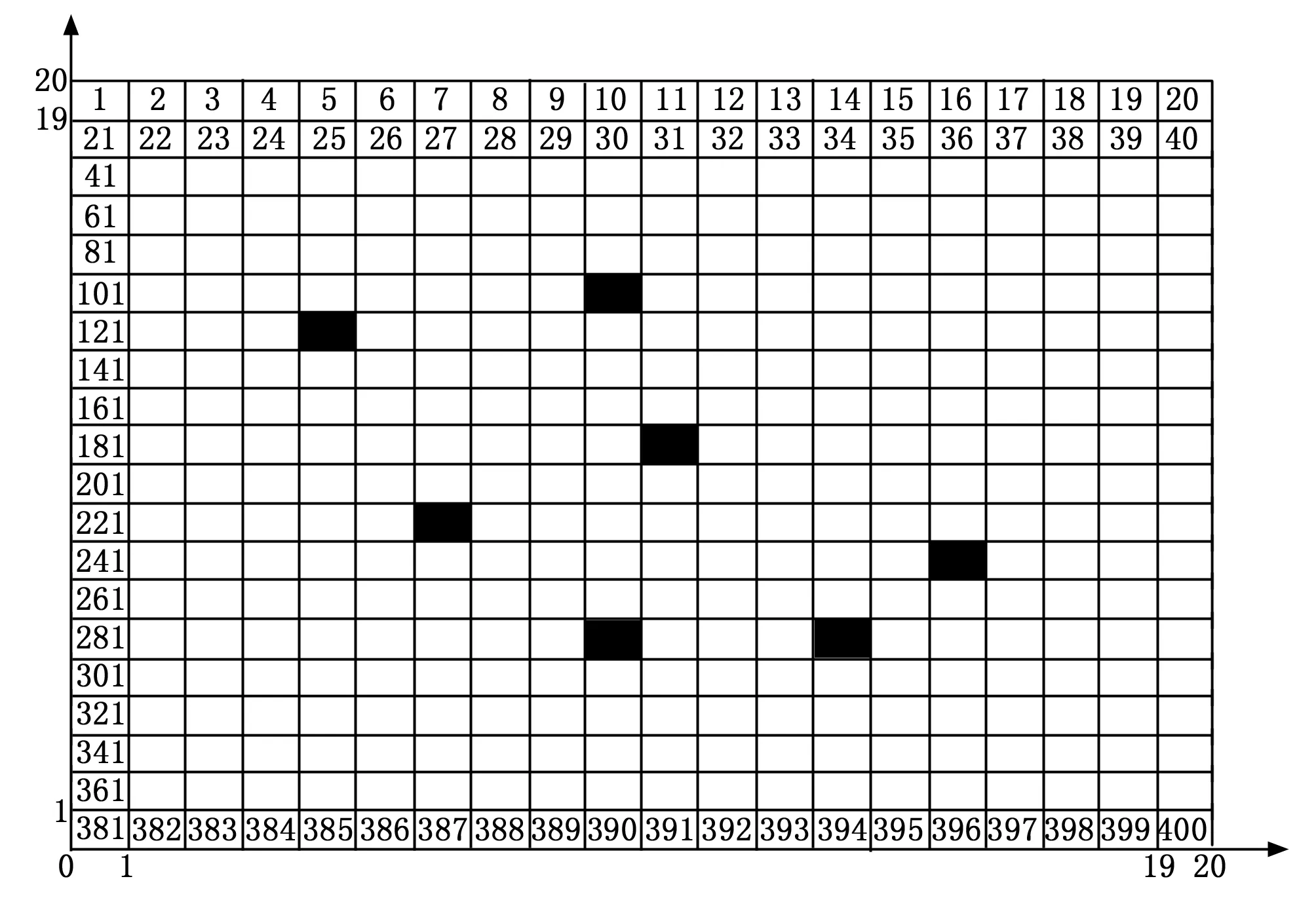
图1 栅格图
3.2 局部信息动态路径规划
3.2.1 动态障碍变化设置
为验证LD-ACA在动态路径变化中相对于T-ACA所展现出的优越性,本节设计了一种动态障碍变化规则,即:把全局环境划分成若干个子区域,并假设机器人在所在位置的子区域行走时,该子区域的障碍状况是固定不变的,机器人所在子区域外的信息与机器人本次路径规划无关。划分的子区域数目越多,则机器人对动态路径障碍适应性越强。
3.2.2 边寻边走策略
鉴于T-ACA是选择所有蚂蚁行走路径中的最优路径后,再沿着最优路径行走,这样它的时效性就会大打折扣。基于以上原因,我们设计了边寻边走的策略,具体策略如图2所示:机器人首先会派出若干只蚂蚁利用局部信息寻找最优局部目标点,找到最优局目标点后,机器人采用被调用蚁群算法(Called Ant Colony Algorithm,C-ACA),寻找到达该最优局部目标点的最佳路径并行走,到达最优局部目标点后判断是否为全局目标点,若是全局目标点则寻优结束,若不是全局目标点,则报告机器人,继续重复上一步骤,直到找到全局目标点为止。
3.2.3 最优局部目标点的指标设定
当LD-ACA的边寻边走策略实施时,最优局部目标点的选取方法在很大程度上决定了是否能够寻找到最优路径,本文以三种最优局部目标点确立原则作对比: 1)传统的轮盘赌算法(Traditional Roulette Algorithm,TRA); 2)改进的轮盘赌算法(Improve The Roulette Algorithm,ITRA) 3)最小值选择策略算法(Minimum Selection Strategy Algorithm,MSSA)。
第三种方法是借鉴贪婪算法思想,提出最小值选择策略算法,核心思想为:以全局目标点为参考变量,选取所有可行的局部目标点中距离全局目标点距离值为最小的点为最优局部目标点,距离计算公式如(3)式:
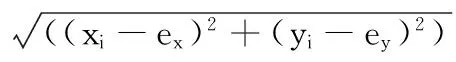
(3)
其中:allowed为排除已经走过的节点后可以前往的局部目标点的集合,ex和ey分别为全局目标点的横坐标与纵坐标,Z为局部目标点到全局目标点距离集合的最小值,以取最小值Z所在的节点位置为最优局部目标点。
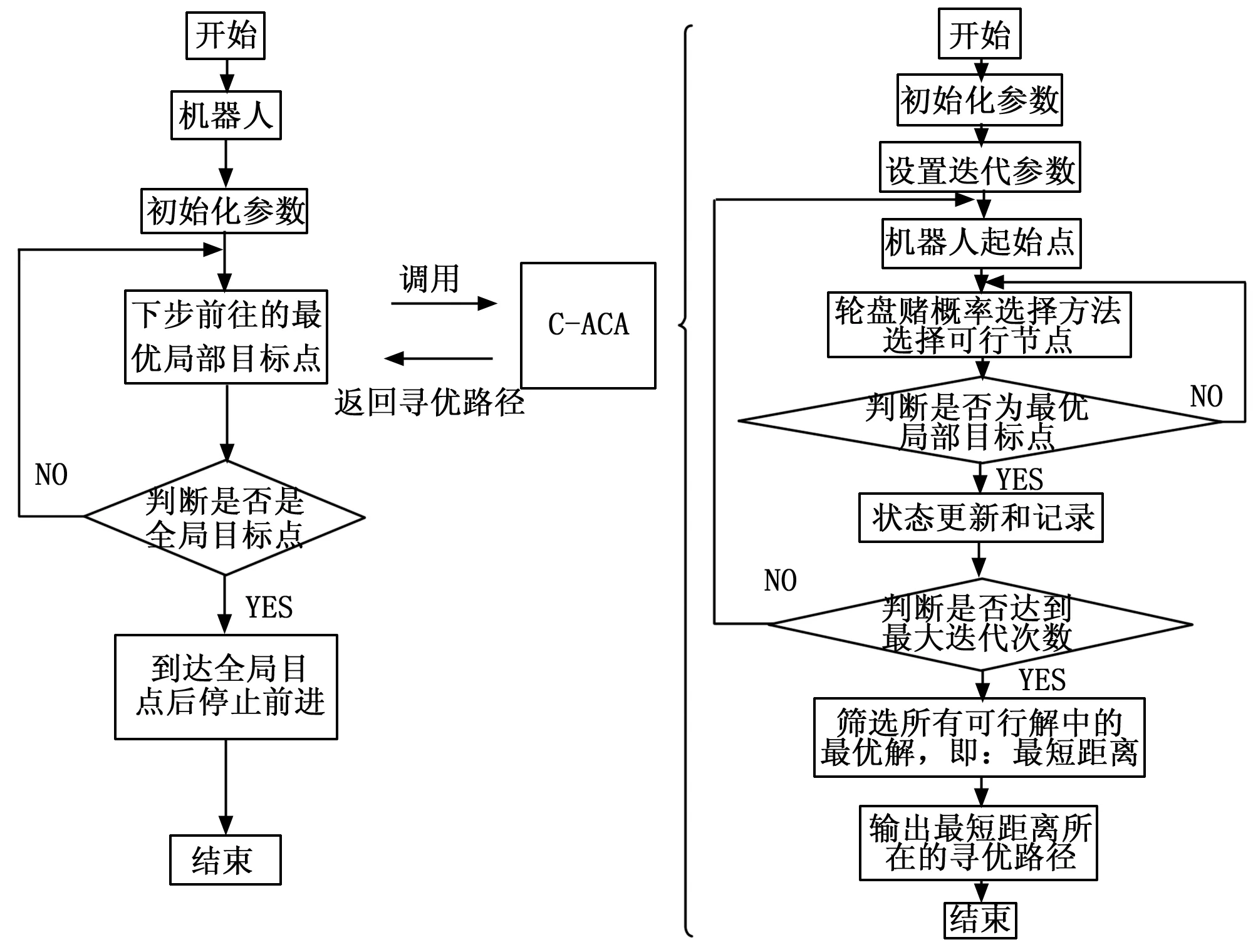
图2 边寻边走策略流程图
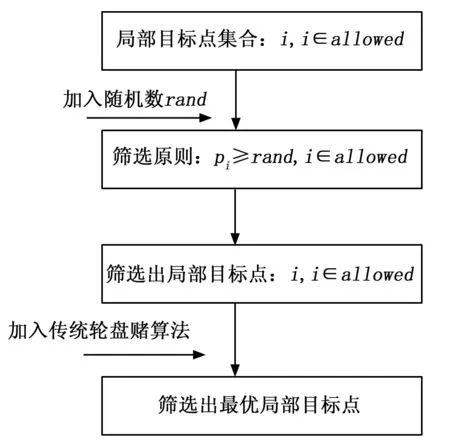
图3 改进轮盘赌算法流程图
3.2.4 C-ACA基本参数设计
3.2.4.1 初始信息素的分布原则
在C-ACA路径寻优过程中,蚂蚁种群在下一步可以前往的节点称为可行节点,可行节点的选取依据主要有两方面:1)当前节点到可行节点路径上的残留信息素浓度。2)可行节点的启发式信息。本节取启发式信息ηij=1/dij,j和i分别为每个小正方形的栅格坐标(节点位置),dij为当前节点i到可行节点j之间的距离。
3.2.4.2 信息素更新和优化原则
C-ACA信息素更新策略只发生在从起始点到最优局部目标点走通的道路上,更新规则如式(4):
τij(t)=(1-R)·τij(t-1)+Δτij
(4)
τij(t)为所有蚂蚁在当前t时刻在可以走通路径(i,j)留下的信息素,τij(t-1)为所有蚂蚁在t-1时刻在可以走通路径(i,j)留下的信息素,Δτij为从t-1时刻到t时刻所有蚂蚁在可以走通路径(i,j)增加的信息素,计算公式如(5)式:
(5)
其中:Lk为第k只蚂蚁迭代过程中寻找到的可行路径,Q为第k只蚂蚁在其自身寻优路径上留下的信息素的总和。同时为了避免蚂蚁种群在某条路径上过于扎堆,导致陷入局部最优解的问题,在信息素初步更新完成后,进行信息素的挥发策略,R为挥发因子。
3.2.4.3 路径选择概率更新规则
由基本的数据可以求得机器人在当前位置节点前往下一个可行节点的公式如(6)式:
(6)
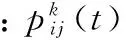
3.2.5 局部可视范围内视野的设置
局部信息的获取方式对于LD-ACA的性能有重大影响,搜索范围越小,对动态环境变化适应性越强。当搜索范围逐步增大到全局环境的范围时,该算法就退化成静态路径规划。为分析局部视野与路径优化的关系,本文设计了两种局部信息获取方式:一步范围视野和两步范围视野,即:一步范围视野是机器人从当前位置只走一步所能达到的范围作为所获得的局部信息;两步范围视野是机器人从当前位置走两步所能达到的范围作为所获得的局部信息。
4 仿真实验与分析
为了验证LD-ACA的特点,本节将T-ACA和LD-ACA分别应用于路径寻优的问题求解。
以每行(列)栅格数为20为例,在本文的LD-ACA中,设置了三种不同的障碍环境G1、G2、G3,三种障碍环境会随着机器人的当前位置变化而变化,障碍环境的变化规律如(7)式:
(7)
其中:xi表示机器人运动所处的横坐标。
算法程序采用MATLAB进行编程测试,算法的各参数由文献[15]得到,初始值设置如表1和表2所示。
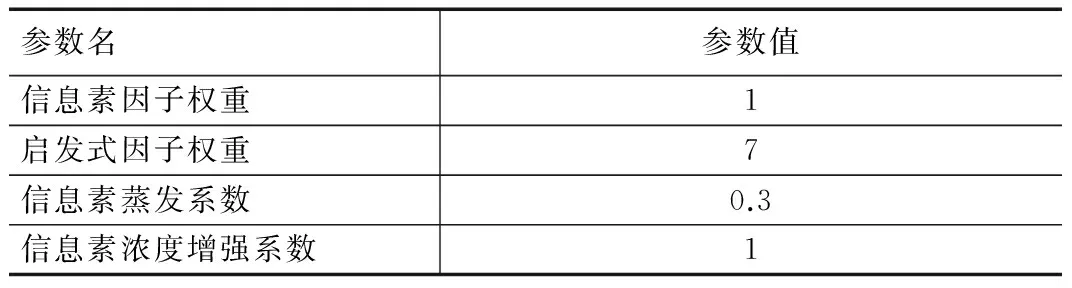
表1 两种算法的公共参数设置

表2 各算法的自有参数设置
4.1 动态环境的性能比较
为方便比较,本节为两种算法设置了相同的算法参数和环境参数:1)两种算法的局部信息获取方式为一步范围视野;2)每行(列)栅格数为20;图4和图5中的曲线为T-ACA在静态环境下的最优路径曲线,而图5中的A曲线为LD-ACA在动态环境下的最优路径曲线,与图5中的B曲线作对比可知,LD-ACA具有自适应动态环境变化的能力,而T-ACA一直按照原来寻优的路径行走没有避开动态障碍物,路径规划失败。为了进一步验证LD-ACA对动态环境变化的适应性,我们再一次改变了环境路况,如图6所示,LD-ACA依然能成功的规划出可行路径,表明了LD-ACA具有较好的动态环境适应能力。
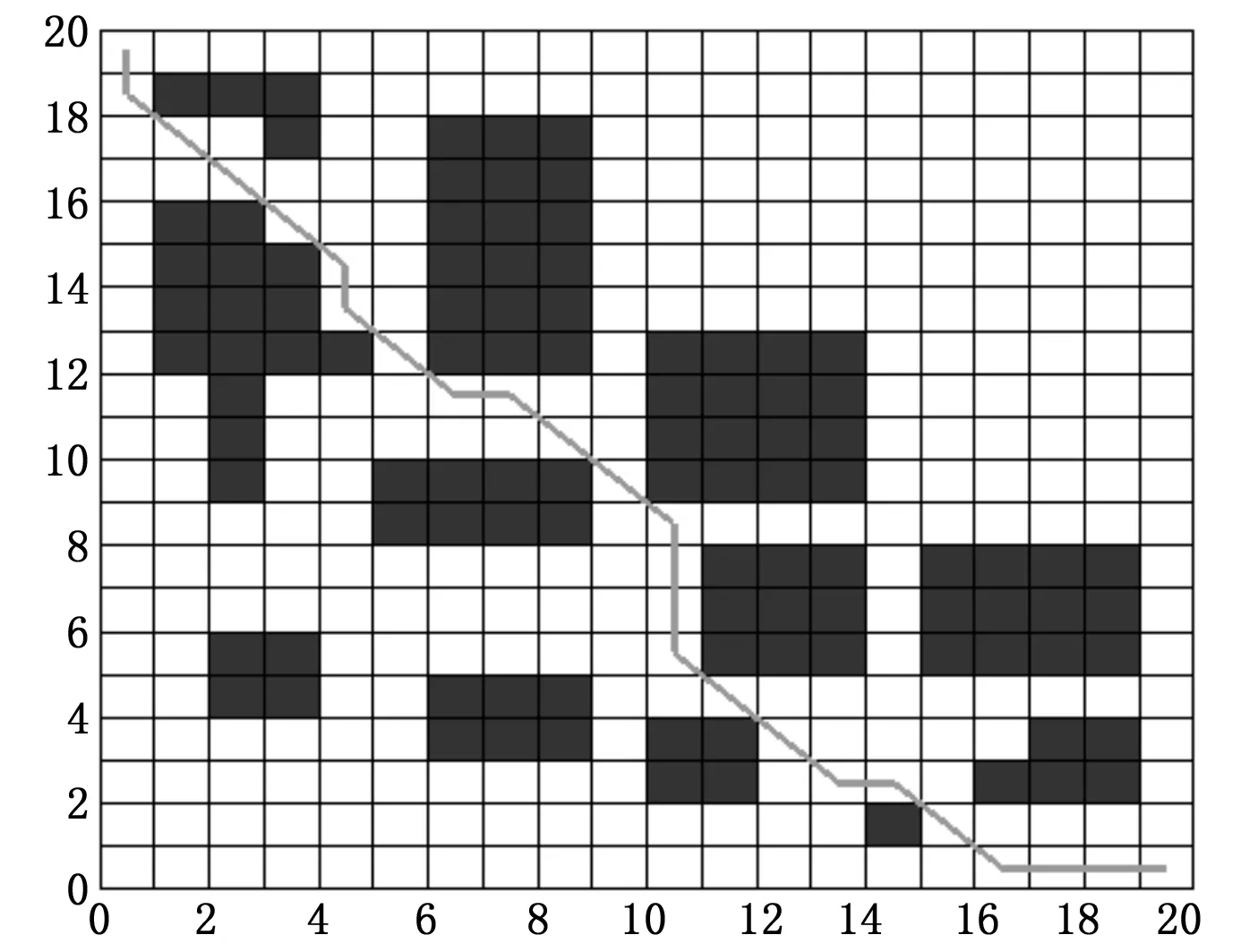
图4 T-ACA寻优路径图
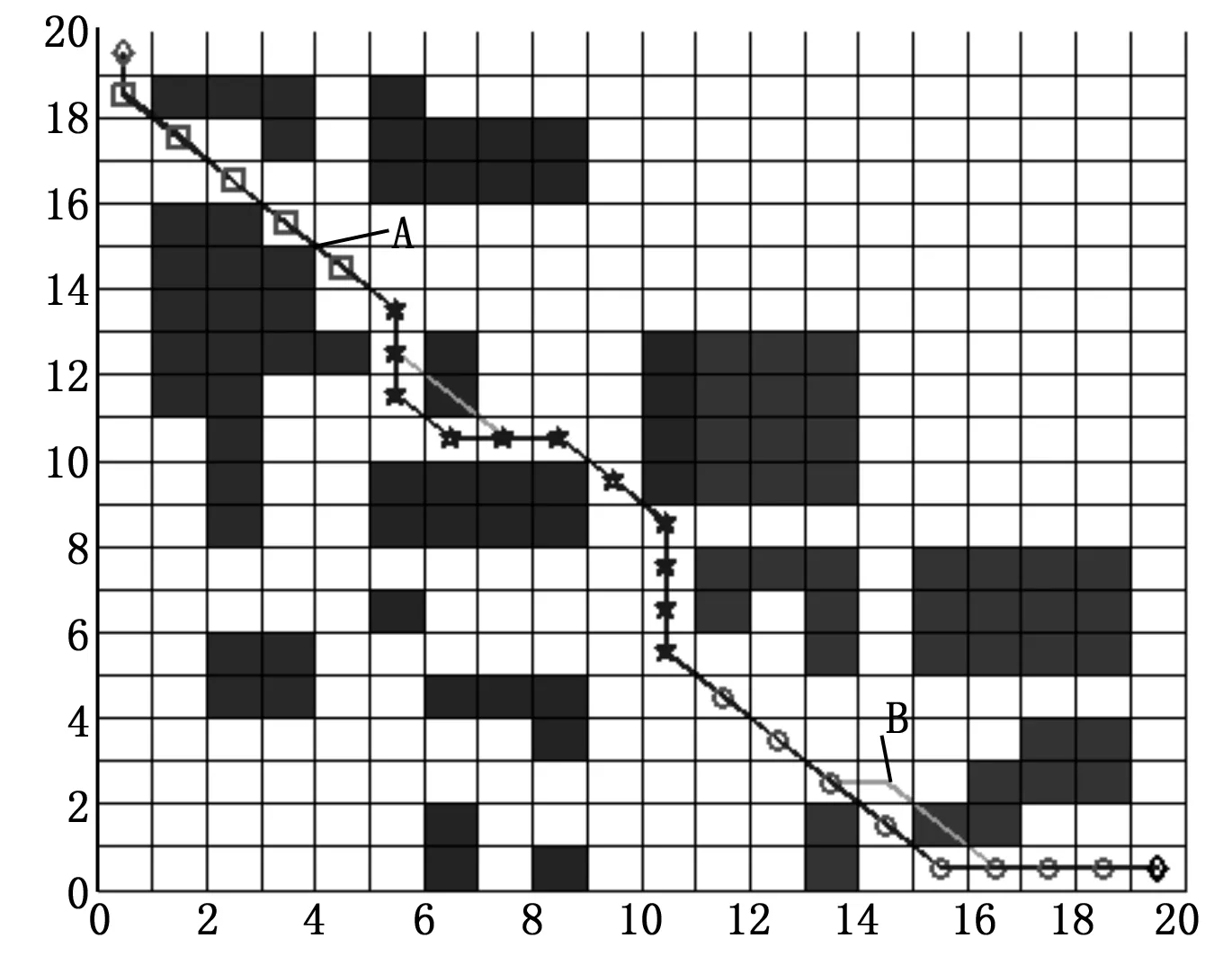
图5 动态路径规划对比图
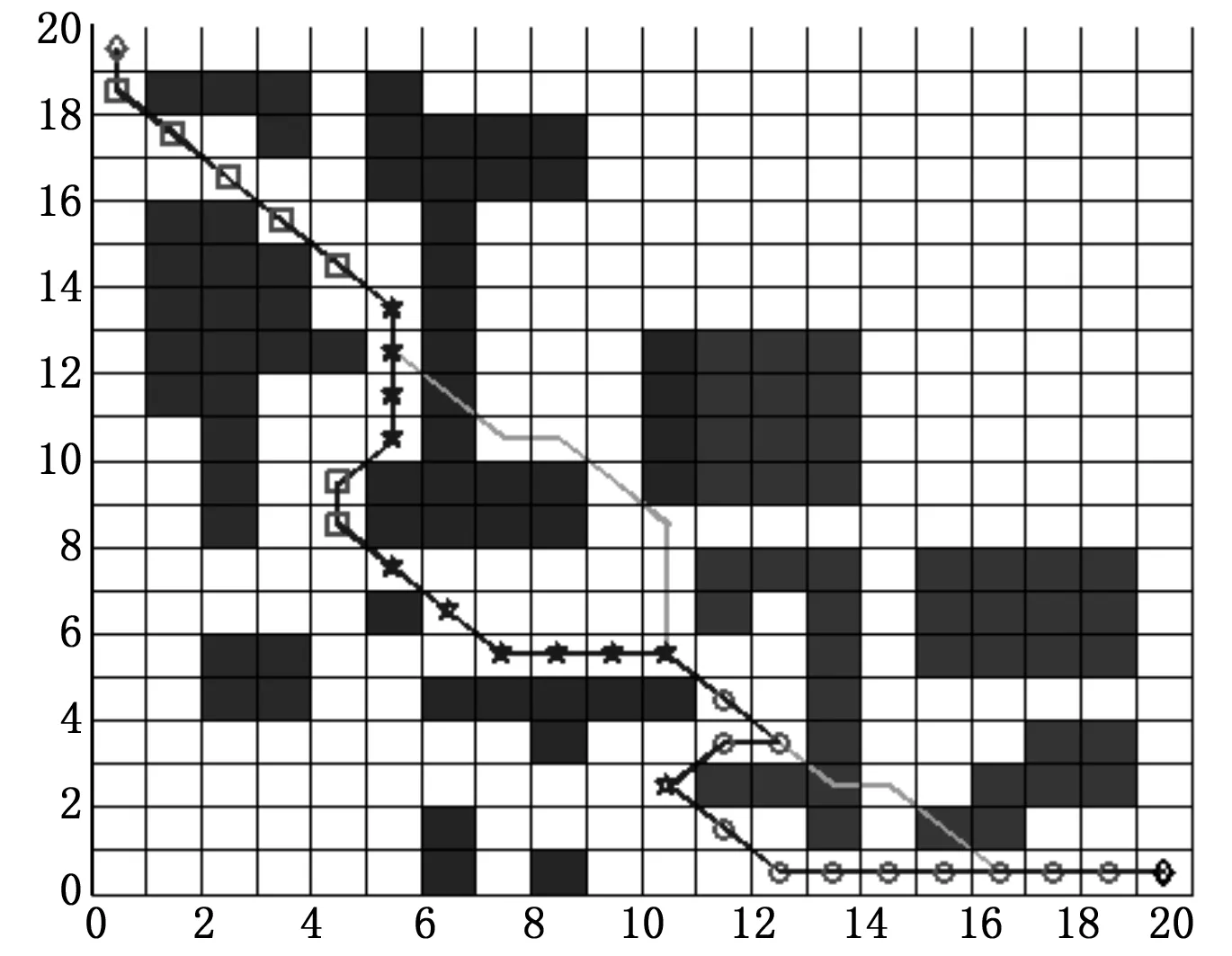
图6 动态路径规划路径寻优对比图
4.2 对动态路径规划的性能优化
4.2.1 三种最优局部目标点选取算法的比较
为验证本文所使用的MSSA在最优局部目标点获取方面的优越性,本文给出了三种最优局部目标点获取算法在不同栅格数目条件下进行50次试验得到的平均值。如图7所示, 以寻优时间为评判指标,可知在栅格数目较小情况下,三者的寻优时间相差不大,当栅格数目大于30时,MSSA的寻优时间明显短于其他两种算法;同理,以最优路径为指标 ,当栅格数目大20时,MSSA找出最优路径显短于其他两种算法。
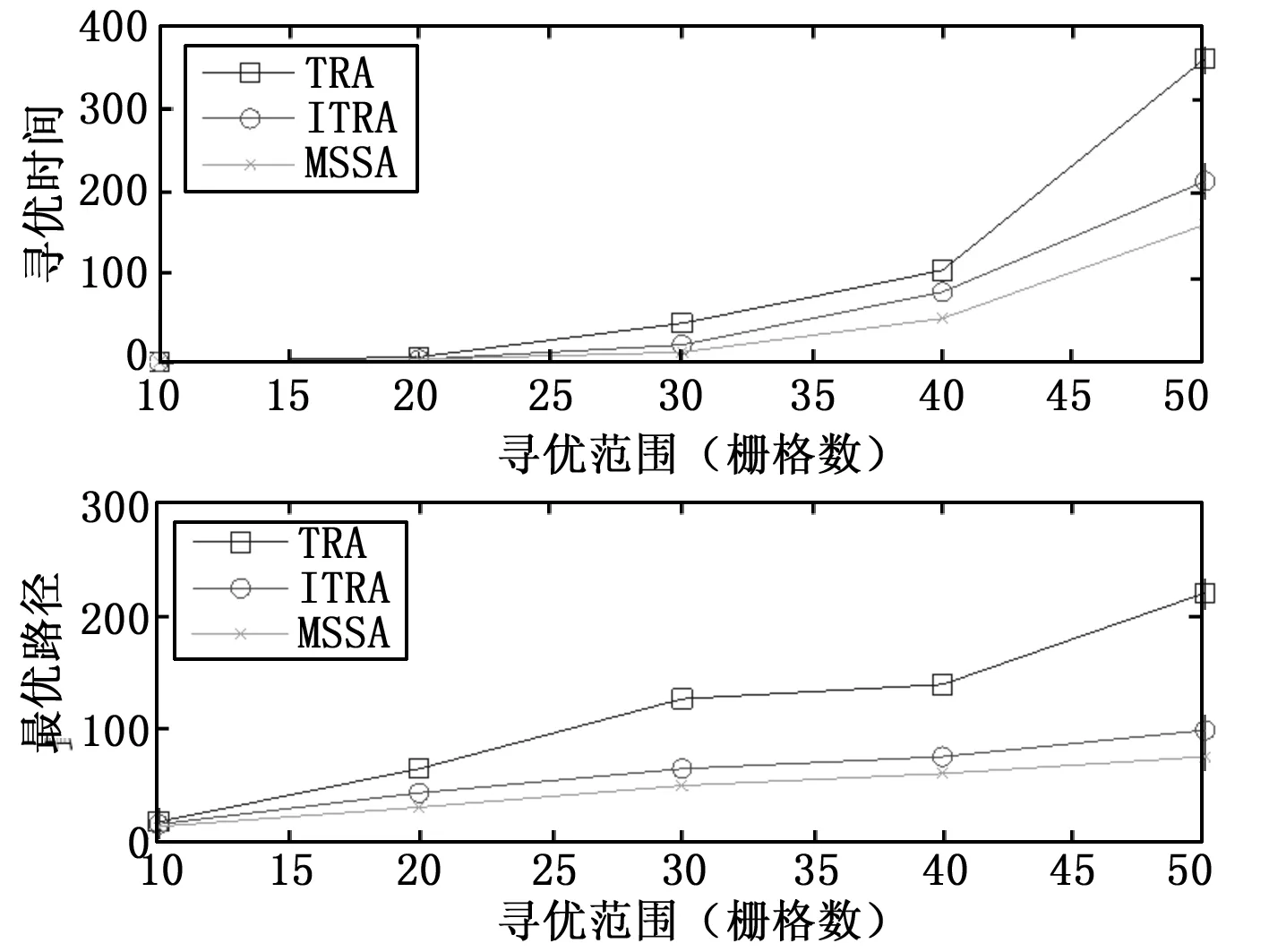
图7 最优局部目标点选择比较图
4.2.2 局部信息搜索范围变化比较
为了验证局部信息的获取范围对LD-ACA的影响,我们把局部信息的获取范围分别设置为一步范围视野和两步范围视野来对比两种条件下的性能优劣。给定的两种算法的相同条件是:1)同等栅格数目;2)最优路径相等或相近。评判指标为:两种算法的寻优时间。图8中的上图的前提条件为每行(列)栅格数目相同,可知在每行(列)栅格数目小于等于20的情况下,二者的寻优时间相差无几,但当每行(列)栅格数目为30、40、50时,两步范围视野算法寻优时间明显短于一步范围算法;同理,图8中的下图前提条件为最优路径相等或相近,可知在最优路径小于等于33的情况下,二者的寻优时间相差无几,但当最优路径超过33时,两步范围算法寻优时间明显短于一步范围算法。但我们应同时看到在两步范围算法的路径寻优过程中,放置的蚂蚁数目和迭代次数都是5,而一步范围算法放置的蚂蚁数目和迭代次数都是2,由此可见,在局部信息获取方式中,搜索范围扩大的代价就是增加了计算负担。
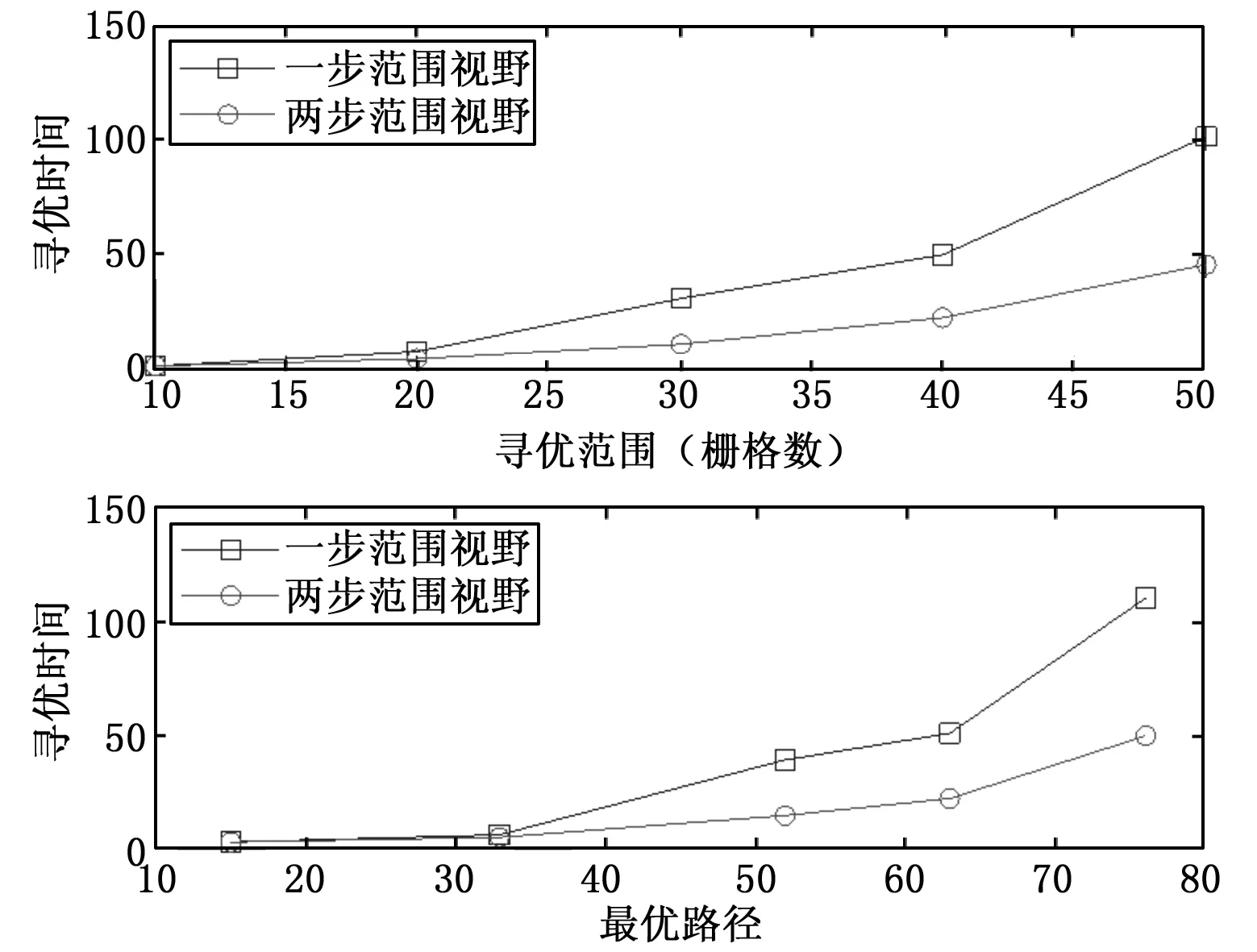
图8 动态路径规划的性能优化图
4.3 静态环境两种算法性能比较
为了验证T-ACA和LD-ACA在不同栅格数目下的性能差异,本节给出了两种算法在静态环境情况下的最优路径性能表,两种算法都在每种栅格数目环境条件下进行了50次的仿真实验,并取平均值。得到如表3所示的仿真结果,由表3可知在每行(列)栅格数小于30,即:栅格数目较少时,两种算法在最优路径和寻优时间两个路径寻优指标上没有太大差别,但当每行(列)的栅格数目大于30时,LD-ACA在仅放置5只蚂蚁和进行5次迭代的情况下的寻优指标就明显优于放置50只蚂蚁进行50次迭代的T-ACA。
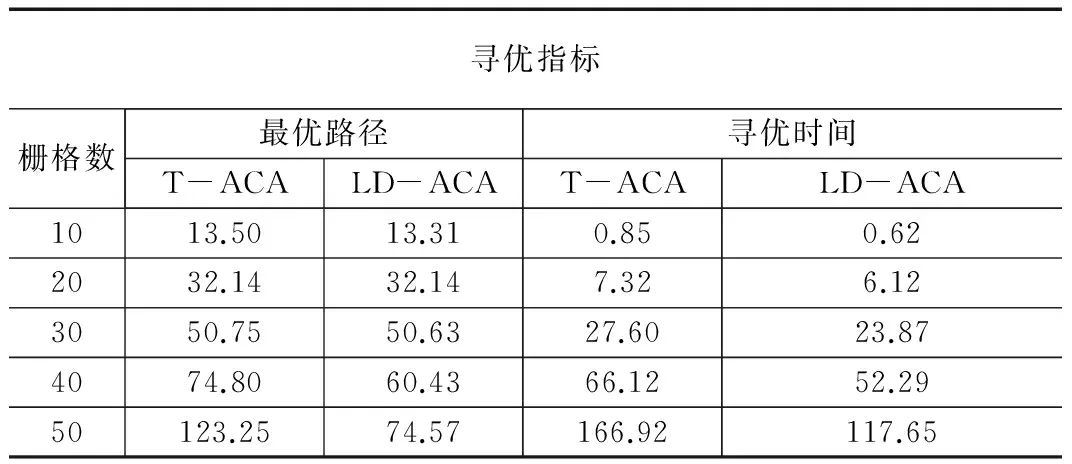
表3 两种算法性能比较
5 结束语
针对T-ACA在动态环境路径寻优的过程中的局限性,本文对T-ACA进行了相应的改进,并以实际的区域交通规划背景为切入点,提出了局部信息动态路径规划的改进蚁群算法,所提出的LD-ACA在保证与T-ACA具有相当的优化效果的同时,能够有效适应障碍变化、大大提高了路径规划的收敛速度。与此同时,对LD-ACA在最优局部目标点选择和局部信息获取两个方面进行了优化,优化方法在保证蚂蚁种群数目和迭代次数没有大幅增加的前提下,大幅度地优化了寻优指标。
[1] 赵开新, 魏 勇, 王东署. 改进蚁群算法在移动机器人路径规划中的研究[J]. 计算机测量与控制, 2014, 22(11):67-70.
[2] 刘营营. 基于模糊神经网络的移动机器人路径规划研究[D]. 沈阳:东北大学, 2012.
[3] 柏 硌, 赵刚要. 基于MapReduce与蚁群优化的航路规划算法[J]. 计算机工程, 2015, 41(5):38-44.
[4] 赵娟平, 高宪文, 刘金刚,等. 移动机器人路径规划的参数模糊自适应窗口蚁群优化算法[J]. 控制与决策, 2011, 26(7):1096-1100.
[5] 袁亚博, 刘 羿, 吴 斌. 改进蚁群算法求解最优路径问题[J]. 计算机工程与应用, 2016, 52(6):8-12.
[6] 基于遗传-模拟退火的蚁群算法求解TSP问题[J]. 计算机测量与控制, 2016,24(3):143-144.
[7] 杨学峰. 蚁群算法求解TSP问题的研究[D].长春. 吉林大学, 2010.
[8] 宋代立, 张 洁. 蚁群算法求解混合流水车间分批调度问题[J]. 计算机集成制造系统, 2013, 19(7):1640-1647.
[9] 周 鹏. 求解置换流水车间调度问题的混合蚁群算法[J]. 计算机工程与应用, 2009, 45(17):191-193.
[10] 屈 鸿, 黄利伟, 柯 星. 动态环境下基于改进蚁群算法的机器人路径规划研究[J]. 电子科技大学学报, 2015(2):260-265.
[11] 王 哲,孙树栋,曹飞祥.动态环境下移动机器人路径规划的改进蚁群算法[J].机械科学与技术,2013(1):42-46.
[12] 柳长安, 鄢小虎, 刘春阳,等. 基于改进蚁群算法的移动机器人动态路径规划方法[J]. 电子学报, 2011, 39(5):1220-1224.
[13] Zhu Q, Hu J, Cai W, et al. A new robot navigation algorithm for dynamic unknown environments based on dynamic path re-computation and an improved scout ant algorithm[J]. Applied Soft Computing, 2011, 11(8):4667-4676.
[14] 葛延峰, 陈 涛, 孔祥勇,等. 改进蚁群算法在城市汽车导航中的应用[J]. 控制工程, 2016, 23(1):133-137.
[15] 叶志伟, 郑肇葆. 蚁群算法中参数α、β、ρ设置的研究——以TSP问题为例[J]. 武汉大学学报(信息科学版), 2004,29(7):597-601.
Local Information Dynamic Path Planning Based on Improved Ant Colony Algorithm
Zhao Feng2, Yang Chunxi2, Chen Fei2, Huang Lingyun2, Tan Cheng2
(1.Kunming University of Science and Technology, Faculty of Chemical Engineering, Kunming 650500, China;2.Kunming University of Science and Technology, Faculty of Land Resource Engineering, Kunming 650093, China)
Considering the limitation of traditional ant colony algorithm’s slowish convergence and bad self-adaptability to dynamic path change, a dynamic improved ant colony algorithm based on local information acquisition strategy is proposed in this paper. Firstly,The local information acquisition strategy is used to obtain the optimal local target point. Then, the improved ant colony algorithm is called to obtain the optimal path in the local region.And the new optimal local target point of the neighbor region is obtained by repeating the loop until the global target point is found. Moreover, the improved ant colony algorithm is applied to the path optimization and obstacle avoidance in dynamic path planning. The simulation results show that the new algorithm proposed not only has considerable path optimization performance compared with the traditional ant colony one, but also has self-adaptive capacity faced with time-vary obstacles and faster convergence speed.
ant colony algorithm; local information; local target point; dynamic path planning
2017-01-19;
2017-02-27。
国家自然科学基金(61364002);云南省教育厅科学研究基金(2016YJS020)。
赵 峰(1990-),男,河北秦皇岛人,硕士研究生,主要从事智能算法方向的研究。
杨春曦(1976-),男,贵州松桃人,博士,教授,主要从事网络控制系统,智能控制方向的研究。
1671-4598(2017)08-0130-05
10.16526/j.cnki.11-4762/tp.2017.08.034
TP393
A

