基于RBF-ARX模型的四旋翼飞行器的预测控制
刘丽丽,左继红,吴 军
(1.中南大学 信息科学与工程学院,长沙 410083; 2.湖南铁道职业技术学院,湖南 株洲 412001;3.长沙理工大学 电气与信息工程学院,长沙 410083)
基于RBF-ARX模型的四旋翼飞行器的预测控制
刘丽丽1,2,左继红1,2,吴 军1,3
(1.中南大学 信息科学与工程学院,长沙 410083; 2.湖南铁道职业技术学院,湖南 株洲 412001;3.长沙理工大学 电气与信息工程学院,长沙 410083)
四旋翼飞行器运行中具有不稳定、非线性和强耦合特性,较难建立其准确的数学模型,针对这个问题,提出了基于RBF-ARX模型的预测控制设计方法;RBF-ARX模型是线性自回归(Auto-Regressive eXogenous,ARX)模型和高斯径向基函数(Radial Basis Function,RBF)神经网络相结合设计的模型,可用于建立非线性系统的全局模型,描述非线性系统的非线性特征。预测控制算法根据系统输入、输出信号预测对象未来输出变化趋势,并将其与系统实际输出的误差反馈校正,使误差最小;该法首先建立四旋翼飞行器的RBF-ARX模型结构,就模型参数的辨识、优化给出了详细分析;并基于该模型设计了系统预测控制器,最后通过仿真和实时控制效果证实了该方法的可行性和有效性。
四旋翼飞行器;RBF-ARX模型;预测控制
0 引言
近年来四旋翼飞行器的型号多样化, 并广泛应用到很多领域[1]。 四旋翼飞行器以自身特点优于其他飞行器,如:具有优异的垂直起降能力,对起降环境适应性强[2];飞行姿态受控于机身的四个驱动电机,使飞行更加平稳[3];四旋翼飞行器无需额外的方向控制系统,其方向随着各个电机的速度改变而改变[4]。但是,四旋翼飞行器是一种强耦合、非线性、复杂的飞行系统,假设模型及控制方法选择不当,将会使其失去平衡[5],严重则引起坠机。因此,如何对四旋翼飞行器建立有效数学模型及有效控制,已经成为该领域的一个热点难点问题。
目前,对四旋翼飞行器控制方法的研究主要包括基于最小二乘算法的四旋翼飞行器控制方法[7]、基于遗传算法的四旋翼飞行器控制方法和基于神经网络 PID 算法的四旋翼飞行器控制方法[8],其中基于神经网络 PID 算法最为常用[9]。
但是,上述方法大部分基于物理模型而进行的研究,由于系统本身的非线性导致很难建立准确的物理模型,影响控制效果。并且上述控制方法较复杂,使得系统动态响应慢、控制误差相对大等缺陷。
针对上述问题,提出基于RBF-ARX模型的预测控制算法,首先建立四旋翼飞行器的RBF-ARX模型,通过离线参数辨识获得模型最优参数,基于该模型设计了系统闭环最优反馈的预测控制器,设定寻优目标函数,得出与期望目标误差最小的预测输出。
1 四旋翼飞行器系统建模、参数辨识及结果分析
1.1 四旋翼飞行器系统介绍
本文所研究对象四旋翼飞行器平台呈十字正交结构,应用于检验建模及控制方法的实验中。如图1所示,为避免飞行器损坏和降低飞行控制的复杂性,锁定其三个自由度。故本飞行器有4个输入,分别是驱动3个水平旋翼和1个竖直旋翼电机的控制电压,3个水平旋翼控制飞行器姿态中的俯仰和翻转角,竖直旋翼控制其巡航方向。系统的输出分别是巡航角翻转角和俯仰角共3个输出。安装在支点处的编码器用于采集并解码姿态信息,与上位机的控制信息进行交换,在MATLAB/Simulink环境下,可以完成控制程序的调试和检验。

图1 四旋翼飞行器本体
1.2 RBF-ARX模型介绍
RBF-ARX模型结合线性自回归(Auto-Regressive eXogenous,ARX)模型和高斯径向函数(Radial Basis Function,RBF)基神经网络,可以描述非线性系统的全局特性,建立非线性系统数学模型,为其控制策略的研究奠定了基础。
对于单输入单输出非线性系统,动态运行过程中输入输出之间非线性变化,根据RBF-ARX建模思想,将每个工作点处的输入和输出局部线性化,则可用ARX模型组来描述动态特性,即:
y(t)=f(X(t-1))+ζ(t)
(1)
式中,
X(t-1)=y(t-1),.....y(t-ny),u(t-1),......
u(t-nu),v(t-1),.....v(t-nv)
其中:输出用y(t)表示,输入用u(t)表示,干扰信号用v(t)表示,ζ(t)是噪声。
将式(1)数学模型用Taylor在某个xo处离散差分后得:
y(t)=[φ0+φ1(X(t-1))]+[Φ0+Φ1(X(t-1))]×
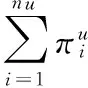
(2)
式中,
(2)式中所示的依存于状态模型的系数,采用神经网络逼近。因为RBF网络逼近非线性标量函数时效果好,可得到RBF-ARX模型如式(3)所示:
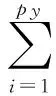
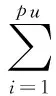
(3)
式中,

1.3 四旋翼飞行器的RBF-ARX模型
对于4输入3输出四旋翼飞行器系统,其RBF-ARX模型如下:
(4)
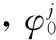
(5)

如式(4)所示的4输入3输出RBF-ARX模型可表述时变的多变量非线性系统四旋翼飞行器的动态特征。采用局部线性化的思想,模型骨架是一个基本线性ARX模型,并采用神经网络函数逼近其回归矩阵的元素。w(t)是模型的指数,体现非线性的变量,主要包括非线性因素,四旋翼飞行器的非线性主要通过俯仰角和翻转角反映,故选取w(t-1)=[p(t-1),r(t-1)]T。
1.4 四旋翼飞行器的模型参数辨识
飞行器RBF-ARX模型中的参数辨识采用一种快速收敛离线的参数分类辨识优化的方法。它是一种列维布格奈奎尔特方法(Levenberg-Marquardt Method ,LMM)[10]和线性最小二乘法(Least Square Method, LSM)[11]相结合的没有限制的结构化非线性参数优化方法(Structured Nonlinear Parameter Optimization Method, SNPOM),这种优化策略步骤如下[12]:
1)参数分类:
模型(4)中的参数被分成线性参数:
和非线性参数:

(6)
令:
(7)
则模型(4)可写成:
(8)
2)模型阶次确定
根据先前经验,m一般选择1~2。采用AIC(Akaike information criterion)信息准则[13],该法常用于估算相应参数值,效果比较好,计算如下:
(9)
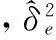
3)初始化
(10)
其中:
(11)
(12)
4)优化
确定目标函数[14]为:
(13)
(14)
寻优过程就是循环计算:
(15)
此时,就得到了模型中的所有参数。
1.5 辨识结果分析
图2所示为RBF -ARX模型对四旋翼飞行器建模的精度。图中y(1)t,y(2)t,y(3)t分别是三个输出角的实际输出与模型预测输出;e(1)t,e(2)t,e(3)t分别代表相应角两者输出误差,为了清晰的看出误差分布情况采用应残差直方图。显然,RBF -ARX模型下系统输出跟随期望输出的效果优良,误差波动范围小且成高斯状分布,建模效果比较理想,建模精度比较高,能很好地描述四旋翼飞行器的非线性动态特性。
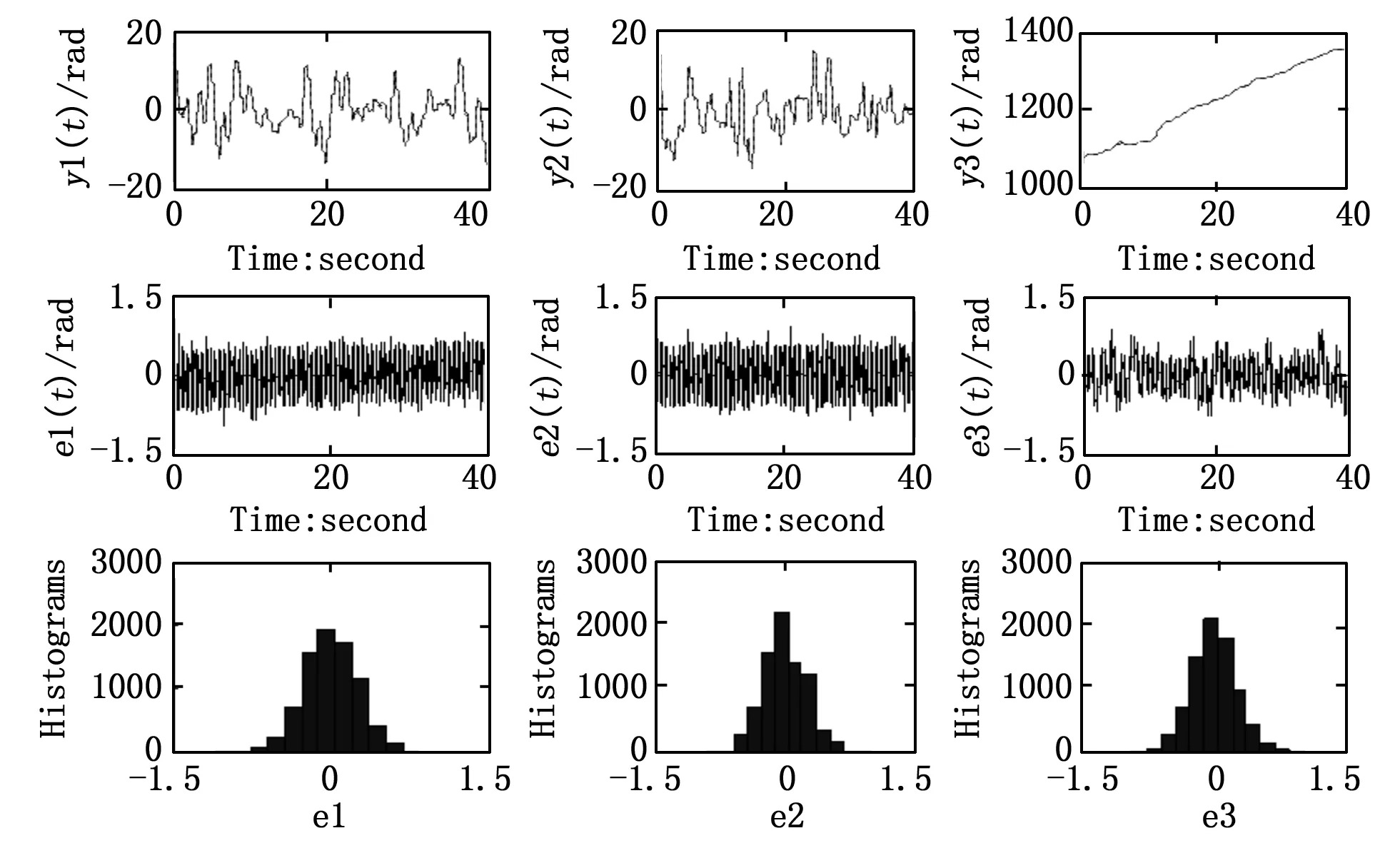
图2 RBF-ARX模型的建模精度
2 基于RBF-ARX模型的预测控制算法
针对复杂非线性系统,可采用基于RBF-ARX模型的预测控制算法,控制结构如图3所示,采用闭环预测输出的一种控制策略。
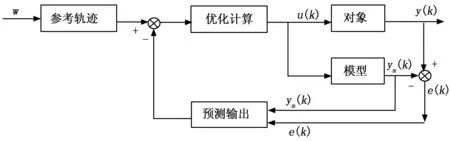
图3 基于RBF-ARX模型预测控制策略的结构框图
图中,采用RBF-ARX模型,根据已知的输入和输出信号预测对象未来输出变化趋势,并将其与系统实际输出的误差反馈校正,再与参考轨迹比较,使系统在未来一段时间内预测输出值与参考期望轨迹之间的误差最小,并优化计算出使性能指标函数最小的控制器的最优输出。
若将模型(4)改写成如式(16)所示的形式[15-16]。
(16)
其中:
(j=1,2)ξ(t)
表示高斯白噪声,满足如下关系式:
E{ξ(t)|Ft-1}=0,E{ξ(t)ξ(t)T}=Ω
(17)
其中:Ft-1表示σ代数,Ω表示有限正值矩阵。
模型(4)则可转换成矩阵形式如式(18)所示:
At(q-1)y(t)=A0,t+Bt(q-1)u(t-1)+Ξ(t)
(18)
其中:q-1表示单位延迟运算符,
(19)
采取预测控制算法得到模型(18)的j步向前预测输出为:
(q-1)u(t+j-1)+y0(t+j|t)
(20)
式中,

(21)
其中多项式:
是方程
(22)
(23)
的解。其中,
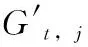
(24)
令:
(25)
其中:Yr(t)是设定的期望输出序列,N1表示预测时域,Nu表示控制时域,且有u(t+j)=u(t+Nu-1)(j≥Nu),由式(20)可得:
(26)
式中,
(27)
确定系统的优化目标函数如式(28)所示:
(28)
式中,权矩阵R(R1或R2)常定义为R=rINu,r通常是一个常数。
实际中,如果只考虑输入限制,可不使用二次规划,控制信号U(t)可表示下式所示:
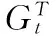
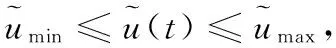
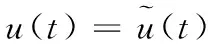
否则:


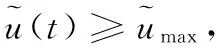
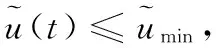
3 四旋翼飞行器基于RBF -ARX模型的预测控制结果分析
3.1 仿真结果分析
针对具有非线性和强耦合的四旋翼飞行器系统,采取基于RBF -ARX模型的预测控制策略。利用MATLAB Sinmulink工具箱建立系统控制仿真结构,运行得到图4、5结果。图4是四个螺旋桨电机的输入电压u1,u2,u3和u4的值,得到图5的y1俯仰角、y2翻转角和y3巡航角的输出结果。
设定俯仰角、翻转角和巡航角目标值为[20,30,40]rad,从仿真结果可以看出,系统的运行效果良好,稳态时的误差为0,过渡时间不长。因此,可以推断该控制方法在实际运行时是可行的。
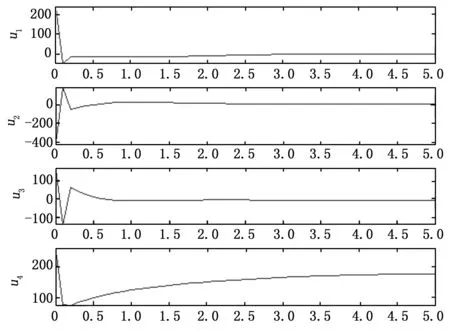
图4 四个螺旋桨电机的输入电压值(V)
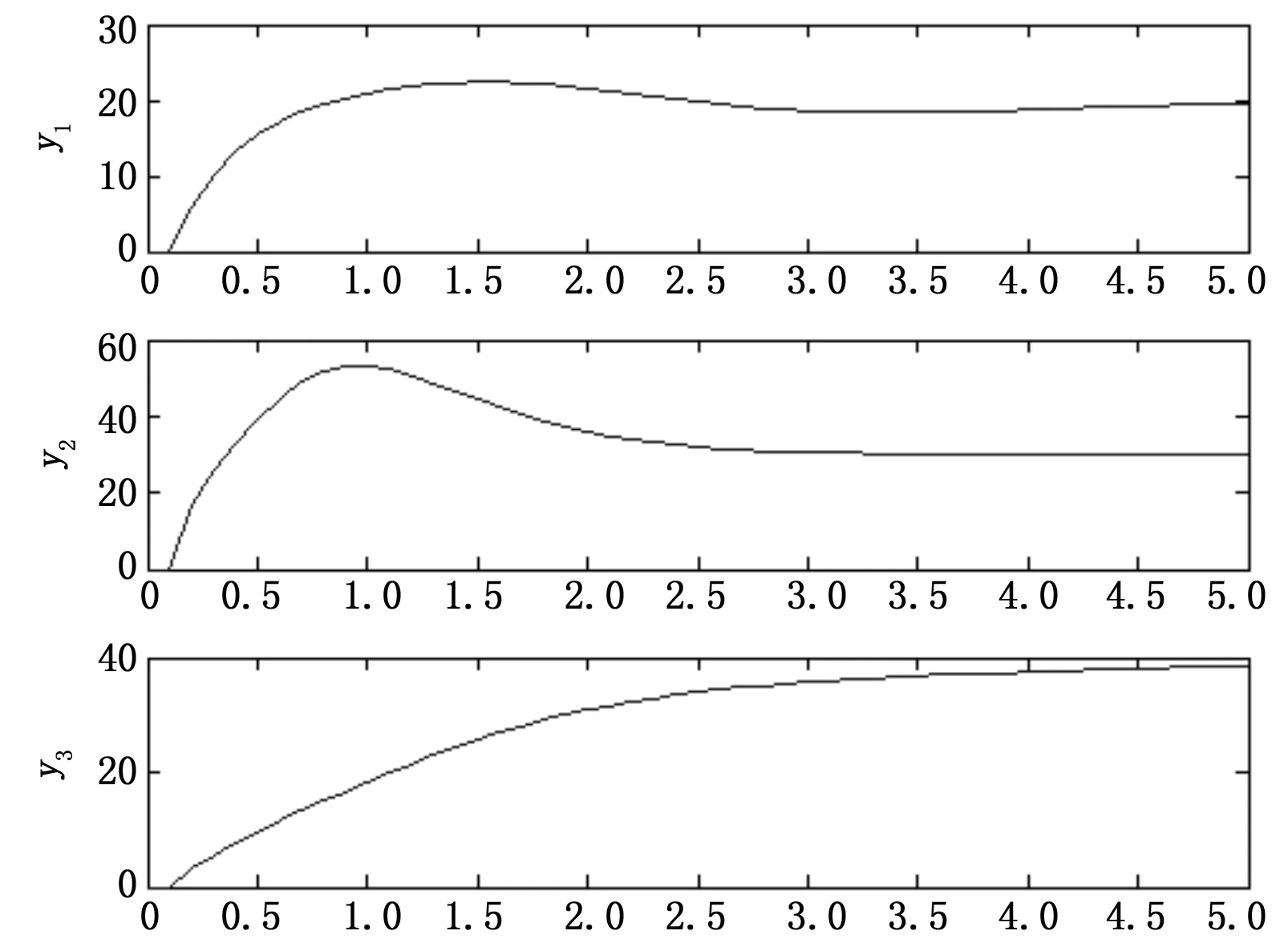
图5 俯仰角,翻转角和巡航角(rad)的仿真输出结果
3.2 实时控制结果分析
控制三个输出角俯仰角,翻转角和巡航角同时变化。将控制器的参数调整到最优。首先使四旋翼飞行器处于初始悬停状态,此时俯仰角,翻转角和巡航角分别为19,21,0(rad),并保持一定时间,然后控制其达到另一目标飞行姿态,此时俯仰角,翻转角和巡航角分别为32,33,10(rad),并保持一段时间,最后再控制其回到初始悬停状态。
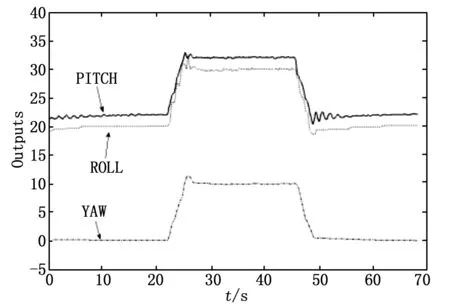
图6 基于RBF -ARX模型的预测控制效果
从图6实时控制曲线可以看出,在初始悬停位置,输出曲线在很小幅度内震荡,之后基本趋向于稳定状态,没有大幅震荡情况出现;控制输出目标突然变化后,其动态响应快速,只有微小超调量;恢复初始水平悬停状态的过程中,未见大幅振荡和超调。表明该建模及控制策略控制效果较好。从图中不难发现,相比其他两个输出角,对巡航角的控制更加平稳,主要与系统的结构特性有很大关系,巡航角主要取决于尾部旋翼的控制,和另外两个角之间没有藕合。俯仰角和翻转角同时受左、右和前部旋翼的控制,且有很强的藕合性,故控制起来相对困难。
4 结语
针对含非线性和不确定性的四旋翼飞行器系统,提出了一种基于RBF-ARX模型的自适应预测控制器的设计方法。采取快速收敛离线参数分类辨识优化的方法得到系统的RBF-ARX模型,基于该模型设计了系统预测控制器。仿真和实时控制结果表明,该方法能很好的描述系统的非线性特性,预测输出值与目标期望轨迹之间的误差很小,验证了该方法的可行性和有效性。
[1] 王 凯,张 维,周德新.基于四旋翼飞行器的飞行航迹规划方法研究[J].计算机仿真,2014,(5): 84-88.
[2] 张雪峰,赵 莉.线性滤波运动舰船图像静态视点平滑过渡仿真[J].科技通报,2014, 12(30) : 148-150.
[3] 王 帅,任振辉.基于改进自适应遗传算法的风电场无功规划优化研究[J].中国农机化学报,2015,36(1):261-265.
[4] 王笑岩,王 石.遗传算法在蔬菜移栽机参数优化中的应用[J].中国农机化学报,2015, 36(1) : 139-141.
[5] 陈磊,霍永亮.利用改进的遗传算法求解约束优化问题[J].重庆工商大学学报( 自然科学版) ,2014, 31(9):63-67.
[6] 吴志琪,董朝阳,贾 臻.基于分叉理论的变体飞行器稳定性分析及控制器设计[J]. 沈阳航空航天大学学报, 2015,32(1): 32-37.[7] 管 萍,刘小河,汪 赛,等.基于模糊系统的高超声速飞行器预测控制[J].控制工程,2014,21(6):823-828.
[8] 王 伟,王 昱,夏 旻.微小型四旋翼无人飞行器姿态控制[J].计算机仿真,2014,31(12): 59-63.
[9] 赵铭明,谢 叶,李梦柯,等.基于DSP的四旋翼无人飞行器控制系统[J].电子世界,2014,(16):19-19.
[10] Marquart D. An algorithm for least-squares estimation of nonlinear parameter[J]. SIAM J Appl, Math,1963, 11:431-441.
[11] 舒迪前.自适应控制[M].沈阳:东北大学出版社,1993.
[12] 徐 仲, 张凯院, 陆 全,等.矩阵论简明教程[M].北京:科学出版社,2001.
[13] 秦宣云,卜英勇,夏毅敏.基于AIC准则优化的径向神经网络微地形曲面重构[J].中南大学学报(自然科学版),2004(10):815-819.
[14] Peng H, Ozaki T, Toyoda Y,et al.RBF-ARX model-based nonlinear system modeling and predictive control with application to a NOx decomposition process[J].Control Engineering Practice,2004, 12:191-203.
[15] Peng H, Ozaki T, Toyoda Y, et al. Exponential ARX model-based long-range predictive control strategy for power plants[J]. Control Engineering Practice,2001,9:1353-1360.
[16] Peng H, Ozaki T, Toyoda Y, et al. Massafumi Mori. RBF-ARX model-based nonlinear system modeling and predictive control with application to a NOxdecomposition process[J]. Control Engineering Practice,2004,12:191-203.
Predictive Control for a Quad-Rotor Helicopter Based on RBF-ARX Mode
Liu Lili1,2,Zuo Jihong1,2,Wu Jun1,3
(1.School of Information Science and Engineering, Central South University, Changsha 410083, China;2.College of hunan railway professional technology, Zhuzhou 412001, China)
The Quad-Rotor Helicopter which is unsteady、nonlinear and coupled with each other makes it difficult to establish accurate mathematical model.for the problem,the design of predictive controller based on RBF-ARX mode were discussed.The RBF-ARX model is a combination model of linear autoregressive (Auto-Regressive eXogenous, ARX) model and Gauss radial basis function (Radial Basis Function) neural network (RBF),It can be used to establish the global model of nonlinear system and describe the nonlinear characteristics of nonlinear system.Predictive control strategy predicts the trend of the system’s output according to the input and output of the system , and the error feedback of the system’s actual output is adjusted to minimize the error.The structure of the RBF-ARX model was built firstly, the parameters’ identification, optimization were analyzed in detail.The predictive controller is designed based on this model.Finally, the simulation results and real time control verify the feasibility and validity of the method.
quad-rotor Helicopter; RBF-ARX mode ; predictive control
2017-01-05;
2017-02-11。
2015年度湖南省教育厅科学研究资助项目(15C0903);2015年度国家自然科学基金(61403045)。
刘丽丽(1985-),女,河南驻马店人,硕士研究生,工程师,主要从事控制科学与工程等方面的教学与科研工作。
1671-4598(2017)08-0079-05
10.16526/j.cnki.11-4762/tp.2017.08.021
TP391.9
A

