基于集对可拓粗糙集方法的高边坡爆破施工安全风险评价

何忠明，刘可，付宏渊，吴从师



基于集对可拓粗糙集方法的高边坡爆破施工安全风险评价

何忠明1, 2, 3，刘可2，付宏渊3，吴从师4

(1. 长沙理工大学特殊环境道路工程湖南省重点实验室，湖南长沙，410114；2. 广西交通投资集团有限公司，广西南宁，530022；3. 长沙理工大学交通运输工程学院，湖南长沙，410114；4. 长沙理工大学土木建筑学院，湖南长沙，410114)

针对高速公路岩质路堑高边坡采用爆破施工开挖方式容易引起边坡稳定性下降而出现边坡坡体垮塌以及因爆破产生的振动作用造成邻近构筑物损坏、人员伤亡等安全风险问题，综合考虑边坡高度、坡形坡率、地质条件、爆破设计方案、爆区环境以及安全监督与管理共6个影响因素，通过确定拟评价样本指标的经典域与节域，构建基于同异反分析的联系度隶属函数，建立基于集对可拓分析方法的安全风险评价模型，采用粗糙集理论计算安全风险评价指标权重，对高边坡爆破施工安全风险进行评价。研究结果表明：工程实例高边坡爆破施工安全风险评价等级为中度风险，与现场调研结果一致；评价方法能真实反映高边坡爆破施工安全风险评价过程中的不确定性，提高高边坡爆破施工安全风险评价的精度；评价模型计算简单，能够为高边坡爆破施工提供风险预判，有效降低安全事故的发生概率，节约工程施工安全防护成本。

集对可拓分析；岩质高边坡；爆破施工；安全风险评价

边坡工程是山区高速公路建设项目中的主要分项工程，对高速公路建设项目的安全生产和运营维护具有十分重要的影响。在岩质路堑高边坡施工过程中，爆破作为主要的开挖方式，产生的爆破振动对岩质路堑高边坡的坡体稳定性以及临近重要构筑物安全性影响的风险评价已成为山区高速公路建设过程中亟需解决的主要问题之一。自21世纪以来，随着我国经济高速发展，基础设施建设越来越多，风险管控技术在国内一些大型土木工程项目中逐渐得到推广和应用。目前，国内现阶段针对山区高速公路工程建设中的岩质路堑高边坡爆破施工安全风险分析尚没有形成一套成熟、系统的评价体系[1−5]。此外，国内学者采用数值分析方法对边坡爆破稳定性或安全性进行分析时，其建立的数值分析模型难以考虑岩石内部的节理、裂隙实际情况，且假设的荷载作用形式也不同于爆破压力实际作用于岩质路堑高边坡的外力荷载形式，导致分析结果有可能与实际情况不太相符[6−10]。为此，本文作者建立基于集对可拓分析方法的高边坡爆破施工安全风险评价模型，采用粗糙集理论计算风险评价指标客观权重，以提高岩质路堑高边坡爆破施工安全风险评价精度，保障公路边坡爆破施工安全。

1 系统建模

1.1 物元可拓基本理论

物元的定义：对于待评价样本，其特征量值为，以有序三元组(，，V)(事物，特征，量值)作为描述事物的基本元，简称物元。若事物以个特征1，2，…，和相应的量值1，2，…，v描 述，则

1.2 集对分析与可拓学耦合模型构建

1.2.1 高边坡爆破安全风险评价指标体系

爆破开挖方式对岩质路堑高边坡坡体稳定性的影响机制主要包括2个方面：一方面，爆破开挖产生的爆破荷载形成外力导致边坡岩体的抗剪力衰减，同时，爆破过程中产生爆破振动，降低边坡岩体结构面的强度，加大边坡失稳的可能性；另一方面，爆破开挖使新形成的坡面更加破碎，并且改变了原有的地应力场，在外界环境影响下，岩体不断风化破裂，边坡的稳定性逐渐丧失[10−14]。另外，由爆破引起的爆破地震效应对临近爆破区建设中的重要建筑物(例如隧道、桥梁等)的不利影响也十分突出，主要是因为此类建筑物还处于在建过程中，强度还未达到设计要求，爆破施工形成的爆破地震效应容易引起严重的安全事故[15−16]。因此，通过对失稳影响机制进行分析，可对岩质路堑高边坡爆破施工安全风险源进行识别。本文选取以下6个主要影响因素构建岩质路堑高边坡爆破施工安全风险评价指标体系。

1) 边坡高度。边坡高度直接影响边坡爆破施工难度，边坡高度越高，施工难度越大，越存在不确定性安全风险。

2) 坡形坡率。当路堑边坡超过所在自然斜坡比拟坡度Δ时容易失稳。高边坡越陡，越不利于边坡稳定，爆破施工安全风险越高。

3) 地质条件因素。高边坡的底层岩性、岩石节理等地质条件因素直接影响高边坡稳定性，地质条件不佳对高边坡爆破施工安全风险影响较大。

4) 爆破设计方案因素。完整的爆破设计方案内容、合理的设计方法、爆破参数、完整且可靠的设计资料能够为高边坡爆破施工安全风险提供确切的技术保证，设计方案越翔实，越有利于降低安全风险。

5) 爆区环境因素。爆区环境因素主要考虑的是爆源与周边重要建筑物之间的关系。岩质高边坡在爆破施工过程中，若爆破区地形复杂，且相邻重要建筑物相对爆源的安全距离较近，则建筑物抗震性能越低，爆破施工风险等级高，其影响不容忽视。

6)安全监督与管理因素。安全监督与管理因素主要考虑的是人员的安全意识与管理制度的完善程度。若安全组织机构设置越科学，专业管理人员的安全生产责任制度、安全规章制度及操作规程的监督和管理越严格，则高边坡爆破施工安全风险越低。

1.2.2 确定拟评价样本指标的经典域与节域

按物元概念，设拟评价样本为1，2，…，N(=1，2，…)，为所有样本集合，C为第(=1，2，…，)个特征(评价指标)；V为样本N关于指标C的量值，则V=(a，b)为N关于特征(评价指标)C所规定的量值范围，即经典域为

相应评价指标C的节域为

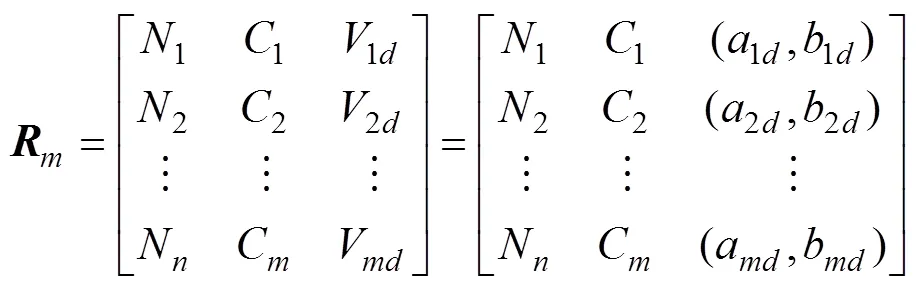
式中：为拟评价样本的全部等级；(a，b)为评价指标C在某条件下所取得的量值范围。

同理可得，拟评价样本整体的同征物元体(=1，2，…，)为

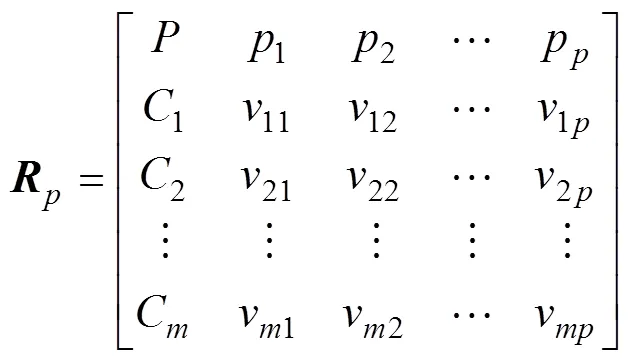
1.2.3 基于同异反分析构造联系隶属函数

集对分析方法是基于三分原理对构成集对的2个集合间关系进行同异反分析，可以整体和辨证统一地刻画确定和不确定性的相互作用和转化关系，与可拓集合存在一定的相似性联系。将高边坡爆破施工现场实地勘察得到的6个影响因素相关数据与讨论标准等级构成的集对与可拓集合论域进行划分，结果如图1所示。

图1 集对同异反分析与可拓集合论域关系示意图

由可拓集与集对同异反分析关系可知：当拟评价样本指标C的实测值x位于讨论等级标准(=1，2，…，)内，则可认为其与标准等级的关系为同一性，同样也位于可拓集合标准正域0=(F，，F,−1)内。因此，相应的联系隶属度函数计算公式为

式中：F，和F，+1分别为讨论等级的左右界限值；μ(x)为拟评价样本对讨论标准等级中指标构成的标准正域的联系隶属度，且μ∈(−1，1)。

当拟评价样本指标C的实测值x位于讨论等级标准的相邻等级−1(＞2)或+1内，同样也位于可拓集合相应的过渡正域1=(F,−1，F,)或者2=(F,+1，F,+2)内时，则可认为其与标准等级的关系为差异性，因此，相应的联系隶属度计算公式为

式中：

式中：F,和F,+1分别为讨论等级的左右界限值；(x，0)和(x，)分别为样本指标C的实测值与讨论标准等级中构成的可拓正域和标准正域的距。式(8)中，当=1时，F,−1取F,；而当=时，F,2取F,。

1.2.4 指标权重计算

对安全风险评价进行研究时，其安全风险评价指标权重的确定是一项十分重要的工作，指标权重计算的客观性直接关系到高边坡爆破安全风险等级评价的准确性。指标权重的计算方法主要有主观权重和客观权重两大类，相应的计算方法有Delphi法、AHP法、均方差法和熵值法等。本文应用基于粗糙集理论的权重计算方法[17−18]来确定高边坡爆破安全风险评价指标权重。该方法无需专家主观经验，在实测数据离散化基础上，利用知识约简方法从数据本身的规律中揭示评价指标的客观权重。具体计算过程如下。

1) 设，由决定的不可区分关系定为ind()，则/ind()={1，2，…，X}，其中的信息量可定义为

式中：card()表示集合所包含的元素个数。

2) 若属性指标a(a∈，{1，2，…，a})的重要性以去掉其后所引起的信息量变化程度来衡量，则公式表示为

在属性中，指标a(=1，2，…，)的权重可定义为

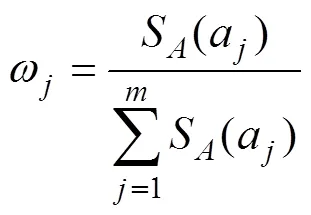
1.2.5 高边坡爆破安全风险评价等级判定

结合拟评价样本指标权重ω，可计算得到拟评价样本综合联系隶属度μ，并根据相应评价等级标准对样本等级进行评定，计算公式如下：

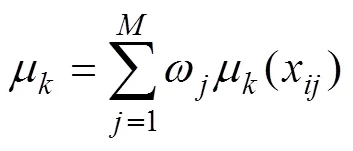
按照式(13)计算所得的综合联系隶属度反映其与高边坡爆破安全风险评级等级符合程度(式中为确定的评价等级[19−20])。

2 实证分析

2.1 工程概况

广西柳南高速公路改扩建工程No.12标段左侧某边坡为岩质边坡，边坡长约150.0 m，高约64.0 m。地层强风化泥质粉砂岩、中风化泥质粉砂岩，岩层产状为183°∠60°，边坡倾向为290°，公路走向为212°，如图2所示。该高边坡距离工区标段内运营高速公路段较近，需进行爆破施工，并按照4个风险等级进行评价，其评价标准={等级Ⅳ(极高风险)，等级Ⅲ(高度风险)，等级Ⅱ(中度风险)，等级Ⅰ(低度风险)}。

通过实地勘测采集到的待评价高边坡爆破安全风险评价指标参数如表1所示。

图2 边坡工程地质剖面图

表1 高边坡爆破安全风险评价指标实测值

2.2 样本高边坡爆破安全风险评价指标经典域Rk和节域Rm的确定

岩质路堑高边坡爆破施工安全风险评价指标共选取6个主要影响因素：边坡高度、坡形坡率、地质条件、爆破设计方案、爆区环境以及安全监督与管理因素。经对实地勘察得到的6个影响因素相关数据大样本统计，得到高边坡爆破施工安全风险评价指标分类标准，如表2所示。

表2 高边坡爆破施工安全风险评价指标分类标准

因此，岩质路堑高边坡爆破施工安全风险评价指标经典域R(其中=4)构建如下：

同理，岩质路堑高边坡爆破施工安全风险评价指标节域R(其中=6)构建如下：

因此，岩质路堑高边坡爆破施工安全风险评价整体的同征物元体R(其中=1)为

2.3 基于同异反分析构造联系隶属函数

根据联系度隶属函数公式(5)~(9)可得以下结果。

2) 待评价No.12标段K1431+320~470左侧坡段中的评价指标2(12)=0，则其位于讨论等级标准∈(0，5)内。由式(5)可知μ(12)=0。

3) 待评价No.12标段K1431+320~470左侧坡段中的评价指标3(13)=12，则其位于标准等级∈(0，24)内。由式(5)可知μ(13)=−0.2。

4) 待评价No.12标段K1431+320~470左侧坡段中的评价指标4(14)=35，则其位于讨论等级标准∈(0，24)相邻等级+1内。由式(6)~(8)可知μ(14)=−0.22。

5) 待评价No.12标段K1431+320~470左侧坡段中的评价指标5(15)=46，则其位于讨论等级标准∈(0，24)相邻等级+1内。由公式(6)~(8)可知μ(15)=−0.44。

6) 待评价No.12标段K1431+320~470左侧坡段中的评价指标6(16)=21，则其位于讨论等级标准∈(0，24)内。由式(5)可知μ(16)=−0.25。

2.4 计算高边坡爆破安全风险评价指标权重

岩质路堑高边坡爆破安全风险评价指标权重的计算采用的是基于粗糙集理论的权重计算方法。这种计算方法以大样本现场勘察数据为准，其计算见文献[12]及式(9)~(11)。本文的指标权重计算结果如表3所示。

表3 高边坡爆破安全风险评价指标权重

2.5 高边坡爆破安全风险评价等级判定

按照式(12)计算得到岩质路堑高边坡爆破安全风险评价的综合联系隶属度为μ=−0.382。

高边坡爆破安全风险评价等级标准如表4所示。据此标准，广西某高速公路No.12标段K1431+320~ 470左侧坡段爆破施工安全风险等级为等级Ⅱ(中度风险)。在现场调研中发现，该样本高边坡在实际爆破施工时，由于爆破施工方案设计中没有使用烈性炸药，而是采用静态破碎剂及二氧化碳气体爆破等新型控制爆破技术，安全风险等级为中度风险，故由本文模型计算判定的风险等级与实际工程情况相符，验证了本文模型的正确性。

表4 高边坡爆破安全风险评价等级标准

3 结论

1)建立的高边坡爆破施工安全风险的集对分析−可拓综合评价模型，通过将可拓学与集对分析理论耦合，真实反映了高边坡爆破施工安全风险评价过程中的不确定性，提高了高边坡爆破施工安全风险评价的精度，并且评价模型分析思路清晰，计算简单。

2)基于粗糙集理论的安全风险评价指标权重计算方法与传统指标权重计算方法相比更加科学、客观，完全依托高边坡施工现场调研得到的大样本本身数据的规律，降低了专家评价的主观因素，能使高边坡爆破施工安全风险评价指标赋权更加科学、可靠，更加真实地反映评价样本的实际情况。

3)基于集对分析和可拓学耦合方法的评价结果与工程实际结果相吻合，验证了本文模型的正确性及实用性。说明本模型能够为高边坡爆破施工提供风险预判，及时地提出相应的解决方案，有效地降低安全事故的发生概率，节约工程施工安全防护成本，使高边坡爆破施工更加的技术可行，经济合理。

[1] 高文学, 刘宏宇, 刘洪洋, 等. 爆破开挖对路堑高边坡稳定性影响分析[J]. 岩石力学与工程学报, 2010, 29(S1): 2982−2987. GAO Wenxue, LIU Hongyu, LIU Hongyang, et al. Road high cutting slope stability analysis under influence of blasting for excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S1): 2982−2987.

[2] 谷慧娟, 邓海斌. 公路岩质高边坡爆破开挖模拟分析[J]. 公路工程, 2013, 38(1): 38−39, 43. GU Huijuan, DENG Haibin. Simulation analysis of blasting excavation for highway rock slope[J]. High Way Engineering, 2013, 38(1): 38−39, 43.

[3] 刘国颂, 綦春明, 聂春龙. 基于博弈论组合赋权的边坡稳定性集对分析[J]. 长江科学院院报, 2014, 31(6): 83−88. LIU Guosong, QI Chunming, NIE Chunlong. Set pair analysis of slope stability based on combination weighting of game theory[J]. Journal of Yangtze River Scientific Research Institute, 2014, 31(6): 83−88.

[4] 林孝松, 赵燕, 陈洪凯, 等. 山区公路边坡安全评价系统设计与实现[J]. 中国安全科学学报, 2014, 24(3): 72−78. LIN Xiaosong, ZHAO Yan, CHEN Hongkai, et al. Design and realization of slope safety assessment system along highway in mountainous area[J]. China Safety Science Journal, 2014, 24(3): 72−78.

[5] 林孝松, 许江, 陈洪凯, 等. 山区公路高切坡整体安全评价方法研究[J]. 武汉理工大学学报(交通科学与工程版), 2011, 35(4): 718−722. LIN Xiaosong, XU Jiang, CHEN Hongkai, et al. Study on the overall safety evaluation method of high cut-slope in mountain highway[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2011, 35(4): 718−722.

[6] 林孝松. 公路边坡安全评价集对分析模型研究[J]. 西南师范大学学报(自然科学版), 2011, 36(6): 28−33. LIN Xiaosong. Study on set pair analysis model of highway slope safety assessment[J]. Journal of Southwest China Normal University (Natural Science Edition), 2011, 36(6): 28−33.

[7] 刘长平. 山区高速公路路堑高边坡稳定性分析评价[J]. 安徽地质, 2010, 20(3): 234−236, 240. LIU Changping. Stability analysis of high slope of expressway in mountainous area[J]. Geology of Anhui, 2010, 20(3): 234−236, 240.

[8] 秦植海, 秦鹏. 高边坡稳定性评价的模糊层次与集对分析耦合模型[J]. 岩土工程学报, 2010, 32(5): 706−711. QIN Zhihai, QIN Peng. Evaluation coupling model for high slope stability based on fuzzy analytical Hierarchy process-set pair analysis method[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(5): 706−711.

[9] 方宏伟, 李长洪, 方玲玲. 基于粗糙商集的边坡稳定性模糊积分评价[J]. 长江科学院院报, 2012, 29(6): 58−62. FANG Hongxin, LIN Changhong, FANG Lingling. Fuzzy integral evaluation of slope stability based on rough set[J]. Journal of Yangtze River Scientific Research Institute, 2012, 29(6): 58−62.

[10] 李宁, 张承客, 周钟. 边坡爆破开挖对邻近已有洞室影响研究[J]. 岩石力学与工程学报, 2012, 31(S2): 3471−3477. LI Ning, ZHANG Chengke, ZHOU Zhong. Influence research of slope blasting excavation on adjacent existed tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(S2): 3471−3477.

[11] 谭国湖, 刘立健, 黄生文. 岩石高边坡爆破震动监测及动力响应分析[J]. 中外公路, 2011, 31(3): 42−45. TAN Guohu, LIU Lijian, HUANG Shenwen. Monitoring of blasting vibration and dynamic response analysis of high rock slope[J]. Journal of China & Foreign Highway, 2011, 31(3): 42−45.

[12] 王广月, 崔海丽, 李倩. 基于粗糙集理论的边坡稳定性评价中因素权重确定方法的研究[J]. 岩土力学, 2009, 30(8): 2418−2422. WANG Guangyue, CUI Haili, LI Qian. Investigation of method for determine factors weights in evaluation slope stability based on rough set theory[J]. Rock and Soil Mechanics, 2009, 30(8): 2418−2422.

[13] 林孝松. 山区公路边坡安全评价与灾害预警研究[D]. 重庆: 重庆大学重庆大学资源及环境科学学院, 2010, 47−87. LIN Xiaosong. Study on slope safety assessment and Hazard warning along Highway in mountainous area[D]. Chongqing: Chongqing University. College of Resources and Environmental Science, 2010: 47−87.

[14] 何海鹰, 胡甜, 赵健. 基于AHP的岩质高边坡风险评估指标体系[J]. 中南大学学报(自然科学版), 2012, 43(7): 2861−2868. HE Haiying, HU Tian, ZHAO Jian. Risk assessment indexes system of high rock slope based on AHP[J]. Journal of Central South University (Science and Technology), 2012, 43(7): 2861−2868.

[15] 刘杰, 宋亮, 毛爱民, 等. 基于模糊层次与改进集对分析的公格尔隧道施工风险评估[J]. 中外公路, 2015, 35(6): 211−216. LIU Jie, SONG Ling, MAO Aimin, et al. Fuzzy AHP and improved set pair analysis based on Kongur tunnel construction risk assessment[J]. Journal of China & Foreign Highway, 2015, 35(6): 211−216.

[16] 王林冰. 基于无网格法的边坡稳定性模糊评价[J]. 水电能源科学, 2014, 32(4): 133−135, 142. WANG Linbing. Fuzzy evaluation of slope stability based on meshless method[J]. Water Resources and Power, 2014, 32(4): 133−135, 142.

[17] 刘晓, 唐辉明, 刘清秉, 等. 考虑能量-时间分布的边坡动力可靠性分析新方法[J]. 岩土力学, 2015, 36(5): 1428−1443, 1454. LIU Xiao, TANG Huiming, LIU Qingbing, et al. A new method for reliability analysis of dynamic slope stability with considering energy-time distribution[J]. Rock and Soil Mechanics, 2015, 36(5): 1428−1443, 1454.

[18] 徐飞, 徐卫亚, 刘造保, 等. 基于PSO-PP的边坡稳定性评价[J]. 岩土工程学报, 2011, 33(11): 1708−1713. XU Fei, XU Weiya, LIU Zaobao, et al. Slope stability evaluation based on PSO-PP[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(11): 1708−1713.

[19] 宋杰, 胡辉, RAFIG A. 基于LiDAR技术的节理岩质边坡有限元分析[J]. 岩石力学与工程学报, 2013, 32(S2): 3972−3978. SONG Jie, HU Hui, RAFIG A. LIDAR-based finite element simulation for jointed rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S2): 3972−3978.

[20] 冯东梅, 陈雪, 王丹, 等. 爆破振动对边坡稳定性影响的FA-IGA-LSSVM模型[J]. 辽宁工程技术大学学报(自然科学版), 2016, 35(7): 717−721. FENG Dongmei, CHEN Xue, WANG Dan, et al. FA-IGA-LSSVM predictive model of the influence of blasting vibration on mine slope stability[J]. Journal of Liaoning Technical University (Natural Science), 2016, 35(7): 717−721.

(编辑 陈灿华)

Safety risk assessment of high slope blasting construction based on set pair-extension analysis

HE Zhongming1, 2, 3, LIU Ke2, FU Hongyuan3, WU Congshi4

(1. Key Laboratory of Special Environment Road Engineering of Hunan Province,Changsha University of Science & Technology, Changsha 410114, China;2. Guangxi Communications Investment Group Co. Ltd., Nanning 530022, China;3. School of Communication and Transportation Engineering,Changsha University of Science & Technology, Changsha 410114, China;4. School of Civil Engineering and Architecture, Changsha University of Science & Technology, Changsha 410114, China)

Considering that the high slope of highway rock cut by blasting excavation is easy to cause the decline of slope stability and the vibration caused by blasting damage to nearby structures, personnel casualties and other security risks,6 factors, i.e. slope height, slope shape and slope ratio, geological condition, blasting design scheme, blasting area environment, safety supervision and management were used to determine the classical domain and joint domain of the proposed evaluation sample, membership function was constructed based on identity-discrepancy-contrary analysis, and a security risk assessment model was established based on set pair-extension analysis method and rough set theory to calculate the safety risk evaluation index weights and evaluate the safety risk of high slope blasting construction. The results show that high slope blasting construction safety risk assessment level is moderate risk, which is consistent with the field survey results. The evaluation method can truly reflect the uncertainty of high slope blasting construction safety risk assessment process, and improve the safety risk assessment accuracy of the high slope blasting construction. The evaluation model analysis is simple, and can provide risk prediction for high slope blasting construction, effectively reduce the probability of safety accidents and save the cost of construction safety.

set pair-extension analysis; high rock slope; blasting construction; safety risk evaluation

10.11817/j.issn.1672−7207.2017.08.032

TK121

A

1672−7207(2017)08−2217−07

2016−09−11；

2016−11−26

国家自然科学基金资助项目(51508042, 51678073, 51274049)；广西交通投资集团有限公司博士后基金资助项目(2016)；长沙理工大学特殊环境道路工程湖南省重点实验室开放基金资助项目(kfj120402)；浙江省交通运输厅科技项目(2014H22) (Projects(51508042, 51678073, 51274049) supported by the National Natural Science Foundation of China; Project(2016) supported by the Post Doctoral Foundation of Guangxi Communications Investment Group Co. Ltd.; Project(kfj120402) supported by the Opening Project of Key Laboratory of Special Environment Road Engineering of Hunan Province; Project (2014H22) supported by the Science and Technology of Department of Transportation of Zhejiang Province)

刘可，博士，研究员级高级工程师，从事高速公路建设管理工作；E-mail: dr_lk@163.com