软弱破碎围岩运输巷道变形机理及修复支护
吴爱祥,胡凯建,黄明清,王贻明,王晶军, 2
软弱破碎围岩运输巷道变形机理及修复支护
吴爱祥1,胡凯建1,黄明清1,王贻明1,王晶军1, 2
(1. 北京科技大学金属矿山高效开采与安全教育部重点实验室,北京,100083;2. 中色卢安夏铜业有限公司,北京,100029)
为解决井下软弱破碎围岩巷道的支护问题,以巴鲁巴铜矿580 m水平运输巷道为研究对象,对巷道稳定性进行监测,分析巷道的变形特征及其影响因素,认为应力集中、围岩软弱破碎、支护强度低以及水的影响是巷道变形的主要影响因素。对巷道变形机理进行研究,建立巷道力学模型,在此基础上结合现场实际提出“钢拱架+长锚索”联合支护方案。使用FLAC3D对修复前后巷道稳定性进行模拟分析。研究结果表明:修复后巷道应力集中区域远离巷道表面,巷道围岩塑性区域面积下降40%。对巷道进行修复并对其稳定性进行监测,60 d内巷道两帮最大收敛变形量为39 mm、顶板最大下沉量为50 mm,没有明显的底鼓发生,巷道变形得到有效控制。
巴鲁巴铜矿;运输巷道;软弱破碎围岩;变形机理;修复支护;数值模拟
巴鲁巴铜矿是一座年设计产能150万t铜矿石的地下矿山,矿位于非洲赞比亚铜带省卢安夏市,原隶属于英国恩亚公司,因其面临矿体倾角较缓、复杂多变以及泥化破碎等开采难题而被迫放弃生产经营[1−3]。2009年,中国有色集团中色卢安夏铜业有限公司通过国际竞标收购取得其控股权并对其进行生产恢复。580 m运输巷道是巴鲁巴铜矿井下运输提升的咽喉,为保证其稳定性,在生产恢复过程中采用U型钢支架支护对其进行了支护,但由于多种因素影响使其在生产过程中出现严重变形,部分区域甚至垮塌,严重影响了矿山正常生产[4]。目前,底鼓、顶板下沉和两帮收敛等巷道变形失稳问题已成为矿山普遍存在的问题[5−7]。国内外学者对巷道变形失稳做了许多研 究[8−10],但是由于巷道的围岩条件和稳定性影响因素的复杂性和不确定性,巷道的变形机理不尽相同。本文作者基于赞比亚巴鲁巴铜矿580 m运输巷道变形失稳的问题,开展巷道变形监测,并对其变形原因及机理进行分析,结合现场实际提出巷道修复支护治理方案,通过数值模拟手段对治理方案的可行性进行分析。经现场实践,巷道变形失稳得到有效控制,保证井下运输提升正常进行。
1 巷道变形特征及影响因素分析
1.1 巷道工程概况
图1所示为巷道平面布置图。580 m运输巷道埋深580 m,受褶皱影响,巷道多次穿过含矿层(白云质片岩)及矿岩过渡带(过渡带片岩)(图1)。各围岩物理力学参数如表1所示。其中,白云质片岩与过渡带片岩岩石强度低,节理裂隙发育,遇水易水化崩解,属于典型的软弱破碎岩体。巷道穿过含矿层区域,其两侧矿体已回采完毕,因采动二次应力导致中央运输道保安矿柱发生应力集中而产生严重变形与垮塌。
1.2 巷道变形特征
巴鲁巴铜矿580 m运输巷道原采用U型钢支架支护,钢支架间距1.6 m,钢支架与围岩间使用木头填充以封闭岩面。支护为被动支护,且部分区域围岩软弱破碎,在采动应力的影响下,巷道发生失稳变形。巷道沿走向方向发生弯曲、垂直走向方向收敛变形严重。巷道收敛过程中伴随有底鼓、顶板下沉现象的发生,测量最大底鼓量可达260 mm;顶板下沉使拱形钢支架变形,测量最大变形量达365 mm,严重区域出现顶板垮冒。对巷道两帮收敛变形进行监测,测点位置如图1所示,监测结果如图2所示。巷道两帮收敛变形大、变形速率大,最大变形速率达14 mm/d。
综上可知:目前的支护手段无法控制巷道失稳变形,巷道断面减小阻碍了井下运输提升,严重影响了整个矿山的正常生产。因此,巷道变形失稳问题亟待解决。
1.3 巷道变形影响因素
通过现场调查分析,认为该巷道变形失稳的主要影响因素如下。
1) 应力集中。巷道顶部120 m和两侧75 m以外的矿岩已基本回采完毕,受采动二次应力影响运输道保安矿柱发生应力集中而产生严重变形与垮塌。
2) 围岩软弱破碎。巷道围岩中,白云质片岩与过渡带片岩属于典型的软弱破碎围岩。由图1可见:巷道多次穿过围岩软弱破碎区,加大了巷道失稳的风险。
3) 支护强度低。巷道采用钢支架支护,形式单一、支护被动,长期被动承载使钢拱架发生变形,无法阻止巷道变形。
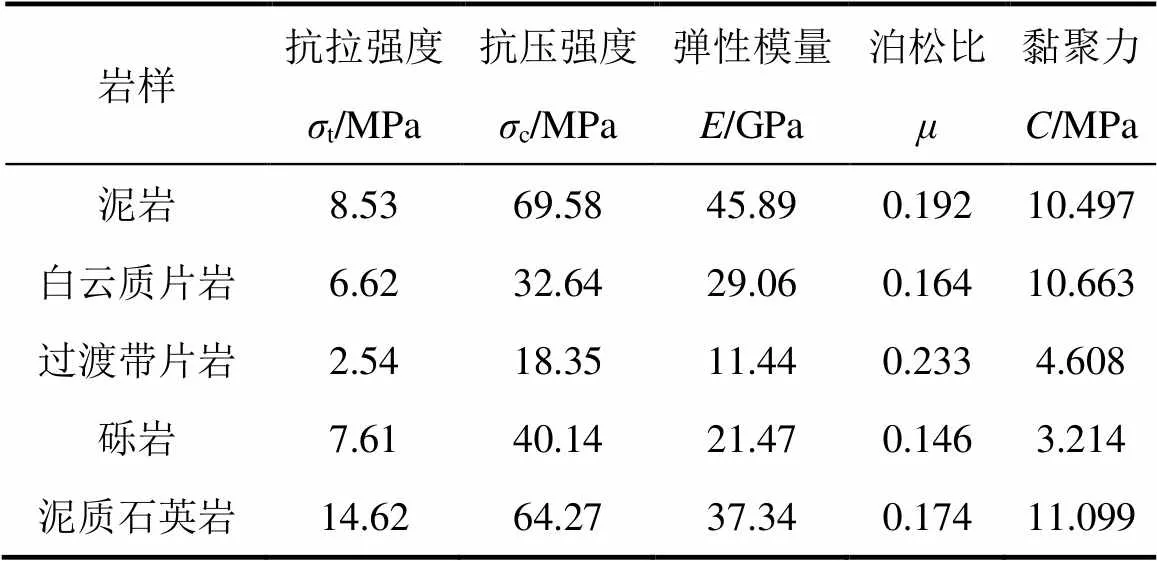
表1 围岩主要物理力学参数

图1 巷道平面布置图
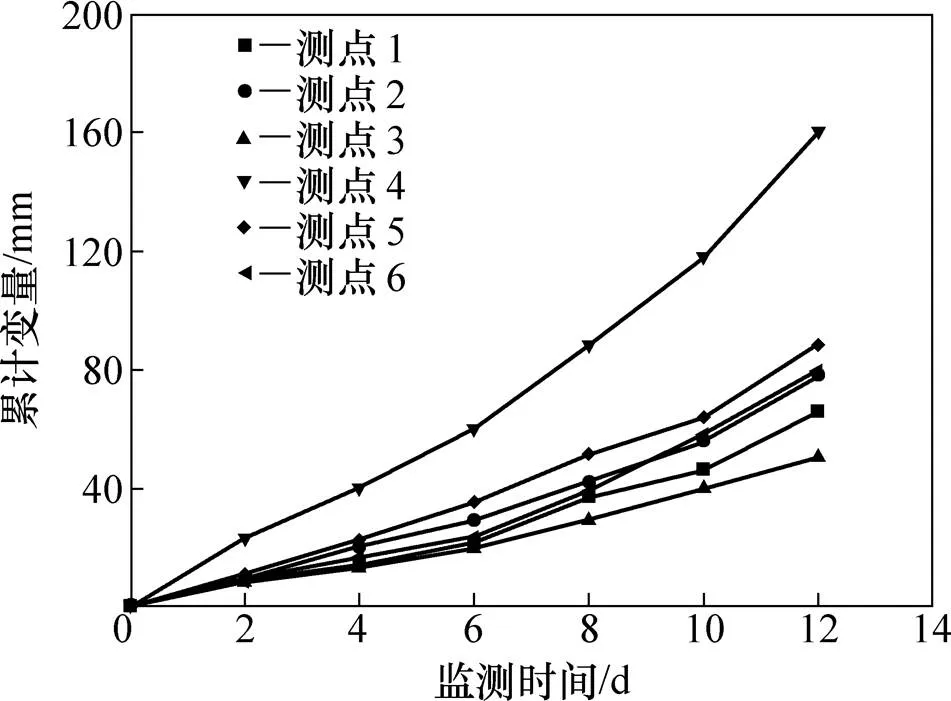
图2 巷道两帮收敛曲线
4) 水的影响。巷道一侧开挖有水沟,浸水后围岩强度降低,特别是白云质片岩与过渡带片岩在遇水后易泥化、崩解,节理裂隙中夹杂物遇水膨胀进一步加剧了巷道变形。
2 巷道变形机理分析
2.1 580 m运输巷道变形力学机理分析
巴鲁巴铜矿580 m运输巷道由于围岩软弱破碎,巷道长期浸泡水中,而钢拱架支护不能提供主动的支护阻力,且未架设底梁,在围岩应力作用下,岩体向巷道内部挤压流动。可将巷道结构从上到下分为3个部分:上部为巷道顶板及上覆岩层,中部为巷道两帮围岩,下部为巷道底板围岩。巷道的开挖导致围岩应力的重新分布,表现为巷道浅部围岩应力下降,往深部出现峰值应力后又逐渐回到原岩应力水平,由此,建立巷道围岩力学模型,如图3所示[11]。当下部岩体承受的上覆岩层自重超过其极限承载力时,岩体中将形成塑性区,并伴随出现连续剪切滑移面。此时,底板中的区域岩体处于极限平衡的塑性状态,当巷道两帮集中应力超过底板岩体的极限承载力时,底板岩体将产生剪切破坏,并沿着连续滑动面从底板向巷道内挤出。580 m运输巷道两帮岩体在应力作用下,发生破碎,破碎围岩起到了卸压作用,有效保护了底板的稳定。围岩破碎后体积增大,岩体沿两帮挤出,巷道出现严重的收敛变形,两帮破碎岩体在高应力作用下逐渐压紧后,应力继续向底板传递,当应力超过底板岩体的极限承载力时,底板将发生剪切破坏,出现底鼓[12],而底鼓将进一步加剧两帮收敛,最终导致巷道断面急剧减小,影响正常生产。

H—原岩应力;K—应力集中系数
2.2 580 m巷道围岩应力场与位移场分析
现假设580 m运输巷道断面为圆形,巷道长度远大于巷道断面尺寸,巷道围岩各向同性且有力学的弹塑性,巷道开挖前围岩处于原岩应力场中,原岩应力。开挖后,围岩应力重新分布,巷道表面径向应力降为0,环向应力增加,所施加支护的反力简化为均布荷载为P,模型如图4所示[13]。
采用非线性的Hoek-Brown[8]强度准则对围岩应力进行分析可知:

式中:σ1和σ3为破坏时的最大、最小主应力;σc为单轴抗压强度;m和s为Hoek-Brown准则中的常数。
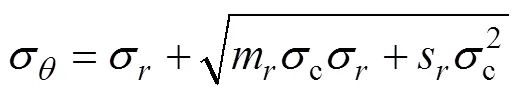
平衡微分方程为
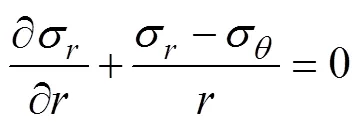
应力边界条件为

由式(2),(3)和(4)可得[14]:
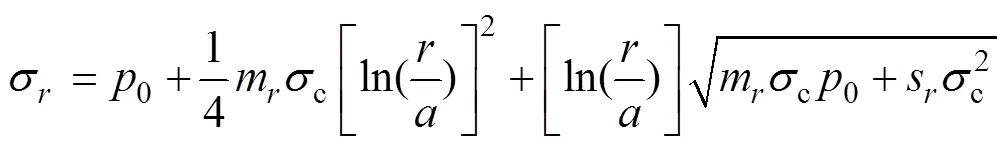
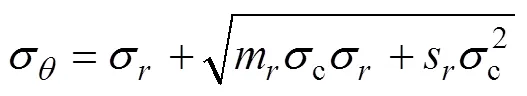
对巷道表面围岩位移场进行分析。采用弹性分析法对图4模型中弹性区与塑性区交界()处径向位移分析为[15]
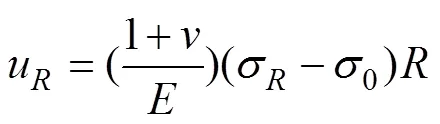
塑性区内任一点的径向位移表达式为
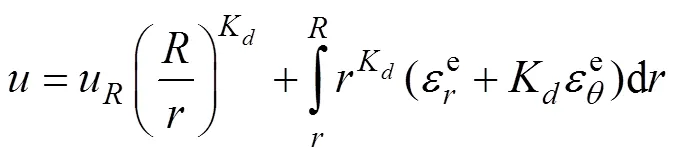
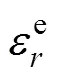
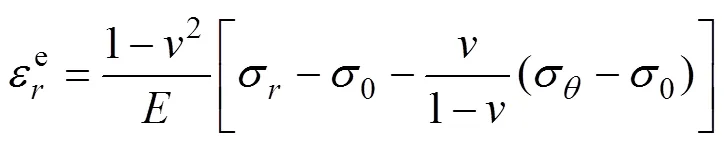
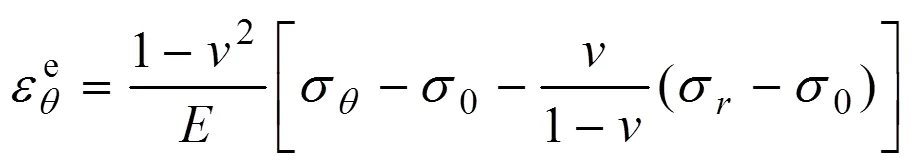
将式(5),(6),(7),(9)和(10)代入式(8)得巷道表面处位移为
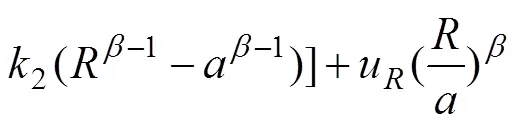
其中:处1=−0,2=0,而弹性区与塑性区交界处位移相对巷道表面位移较小,忽略u后将式(11)简化,得巷道表面位移为[17]
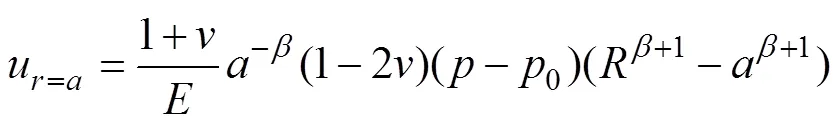
由式(12)可知:巷道所受支护反力0越大,则0越小;巷道围岩的塑性区半径越小,则0越小。巷道应力是影响巷道稳定的重要因素之一,降低巷道表面的应力集中、使应力峰值向围岩内转移也是控制巷道变形的有效措施。故要使巷道变形得到控制,必须降低巷道表面的应力集中,同时增强支护以阻止巷道变形、控制巷道塑性区发展以增强巷道的稳定性。
3 巷道修复支护研究
3.1 巷道修复原则
580 m运输巷道作为主要运输巷道,无法完全停运进行修复支护。为节约施工时间,同时避免修复过程中出现大规模垮冒,在原有支护基础上进行对巷道进行修复支护。通过对巷道变形机理分析,结合现场工程实际,提出“钢拱架+长锚索”联合支护的修复方式:
1) 更换变形弯曲的钢支架,架设底梁;变形严重的地段增加钢支架支护密度。
2) 采用长锚索支护,提供主动支护以减小围岩松动变形、提高岩体自承能力,缓解钢支架受力。
3) 铺设排水管路,改变巷道积水现状。
3.2 巷道修复支护方案
“钢拱架+长锚索”联合支护方案如图5所示。具体参数如下:
1) 原钢拱架间距保持不变,顶梁和柱腿搭接长度大于400 mm,搭接处用卡箍固定;对局部变形严重地段,在原有钢拱架之间补装一架钢拱架。
式中,Kj、Dj、Xj和 Aj分别为第 j指标的变异系数、均方差、均值和权重值。最后,在上述基础上,得到生态安全的综合评价值,公式为:
2) 为钢拱架架设底梁,钢拱架与底梁在井下安装完成后通过焊接连接;钢拱架之间用5根连接板固定,拱顶1根,两帮各1根。
3) 长锚索采用尺寸为15.2 mm×5 700 mm(直径×长)的钢绞线,两帮各3根,孔间距850 mm,排距1 200 mm,孔径45 mm,全长注浆。
4) 钢拱支架与岩石接触面间隙在支护后采用木刹刹紧。
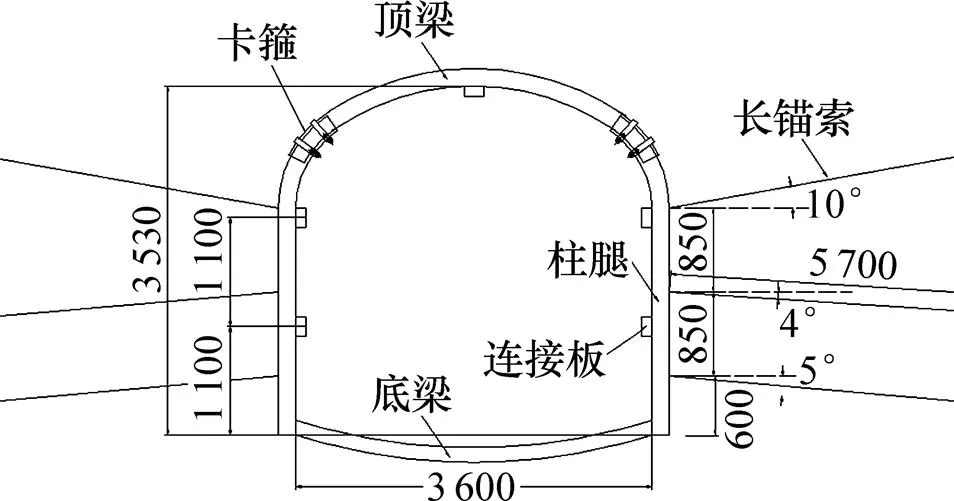
图5 巷道支护设计图
3.3 修复前后巷道稳定性分析
为了分析修复支护方案的可行性,对修复支护前后巷道的稳定性进行数值模拟分析,利用FLAC3D建立计算模型进行模拟,对比分析修复前后巷道应力、塑性区的变化情况。
1) 围岩应力分析。修复前后巷道最大和最小主应力分布分别如图6和图7所示。
由图6可见:修复前,巷道最大主应力在巷道周边岩体中释放,且在顶底部均呈拱形分布:巷道顶板中央最大主应力达到28.113 MPa,出现在距离巷道顶部3.6 m处;巷道的直接顶板最大主应力在7.9~10 MPa左右,分布在巷道两帮中央及底板中央。修复后,巷道周边最大主应力峰值略有降低且在周边分布更为均匀,同时最大主应力集中峰值为26.515 MPa,集中区域距顶板5.3 m,距巷道表面距离增加47%,应力集中区域远离巷道表面向围岩深部转移,可实现对巷道表面卸压,巷道表面变形可得到有效缓解[11]。

(a) 修复前;(b) 修复后
由图7(a)可见:修复前,巷道的最小主应力在巷道直接顶板处分布较为明显,而且在巷道顶板、两帮及底板中央均出现了明显的拉应力分布区,最大拉应力0.42 MPa,说明在巷道周边易出现局部的冒顶片帮以及底鼓现象。从图7(b)可知:修复后最小主应力分布状况与修复前类似,但最小主应力峰值已减弱为0.23 MPa左右,比修复前减弱45%,即修复后最小主应力分布形式虽未改观,但其冒顶片帮的程度减弱了45%,极大促进了巷道的稳定。
2) 塑性区分析。修复前后巷道的塑性区分布如图8所示。巷道塑性区呈对称分布,塑性区均以剪切破坏为主,拉伸破坏为辅,拉伸破坏仅分布在贴近巷道壁面的一层围岩里。修复后的塑性区面积明显缩小,较修复前下降40%。修复前两帮的塑性区向围岩内延伸达2 m以上,修复后两帮塑性区仅向围岩内延伸1.2 m,修复后巷道塑性区范围减小,巷道稳定性得到明显改善。
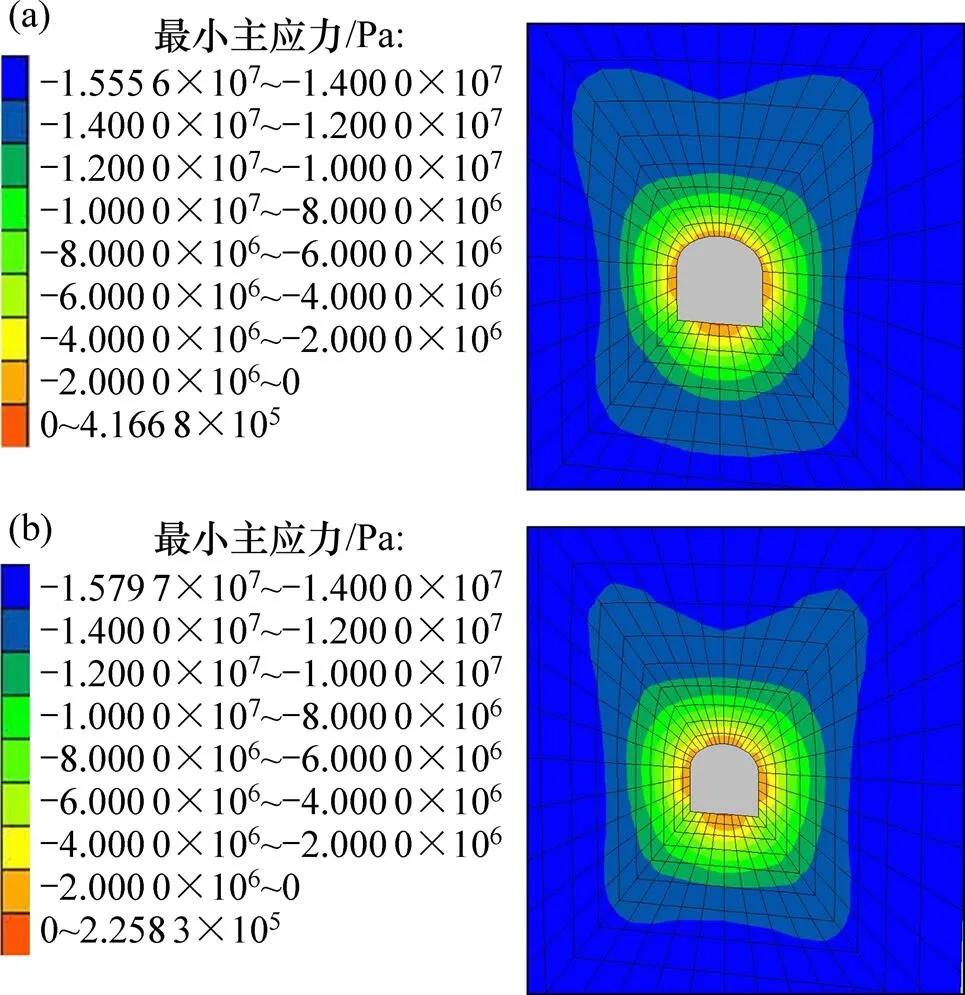
(a) 修复前;(b) 修复后
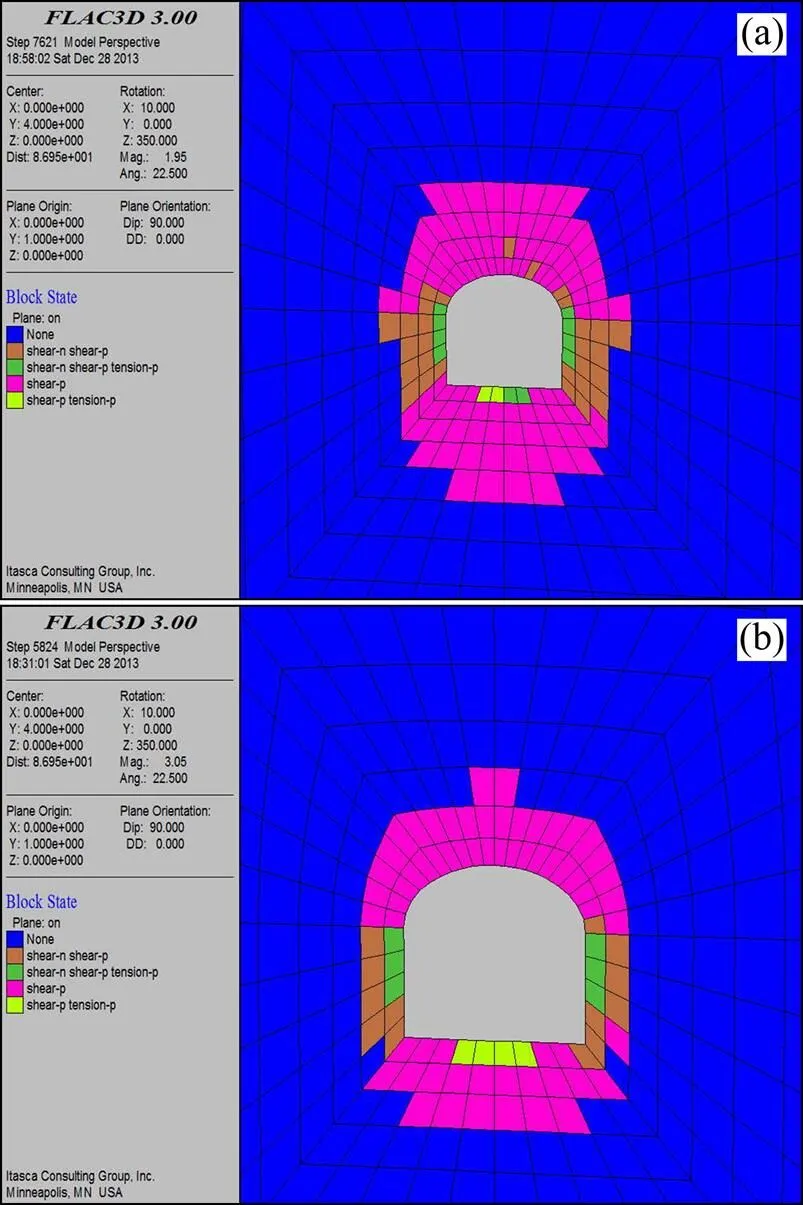
(a) 修复前;(b) 修复后
综上分析,修复后巷道最大主应力集中峰值为26.515 MPa,集中区域距顶板5.3 m,距巷道表面距离增加47%,应力集中区域远离巷道表面向围岩深部转移;修复后最小主应力分布形式虽未改观,但其冒顶片帮的程度减弱了45%;修复后的塑性区面积明显缩小,较修复前下降40%,巷道稳定性明显改善,可知针对580 m运输巷道的修复支护方案是可行的。
4 现场方案实施
根据修复支护设计方案对580 m运输巷道进行修复支护。为保证施工安全与正常生产,每次巷道返修区域控制在3~4 m范围内。返修时,使用支柱牢固支撑钢拱架顶梁,防止垮冒,更换变形的柱腿,架设底梁并将底梁与柱腿焊接;安装预应力注浆长锚索后,充填刹帮木,完成修复。
通过对修复后巷道进行60 d的变形监测得出,巷道经过修复加固后整体稳定性得到了加强,巷道顶板最大下沉量仅为50 mm,没有出现明显的底鼓现象。两帮收敛监测如图9所示。由图9可知:60 d内巷道最大收敛变形量为39 mm,平均变形量22 mm,平均变形速率0.37 mm/d。巷道逐渐趋于稳定,修复支护有效控制了巷道变形失稳。
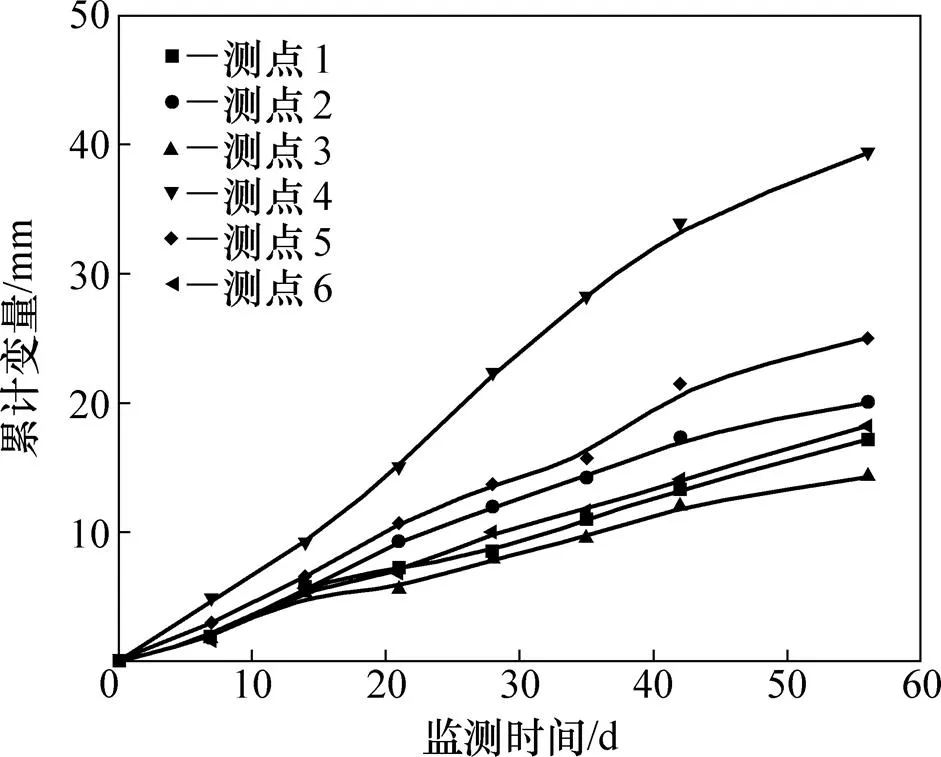
图9 修复后巷道两帮变形曲线
5 结论
1) 巴鲁巴铜矿580 m运输巷道变形主要表现为巷道两帮收敛,伴随出现顶板下沉和底鼓现象,严重区域发生垮冒;影响巷道变形的主要因素有应力集中、围岩软弱破碎、支护强度低以及水的影响。
2) 对580 m运输巷道变形机理进行分析,认为在应力作用下巷道两帮围岩发生破碎变形,应力向巷道底板传递导致底板发生剪切破坏,产生底鼓,底鼓进一步加剧了巷道两帮收敛。为控制巷道变形,需降低巷道表面的应力集中、使应力峰值向围岩内转移,同时控制巷道塑性区发展。
3) 结合现场实际情况,确定巷道修复支护采用“钢拱架+长锚索”联合支护方式。通过数值模拟分析了修复支护方案的可行性,结果表明支护方案可有效控制巷道表面的应力集中使其向深部转移,应力集中区域距巷道表面距离增加47%,同时降低了塑性区域面积使其较修复前下降40%,修复后巷道稳定性明显得到改善。
4) 采用“钢拱架+长锚索”支护方案对巷道进行修复支护后,60 d内巷道两帮最大收敛变形量为39 mm,巷道顶板最大下沉量仅为50 mm,没有出现明显的底鼓现象,巷道的变形得到有效控制。
[1] 王晶军, 李云生. 巴鲁巴铜矿本地化建设实践[J]. 有色矿冶, 2015, 31(1): 54−57. WANG Jingjun, LI Yunsheng. Practice of localization strategy in Baluba Copper Mine of CLM[J]. Non-ferrous Mining and Metallurgy, 2015, 31(1): 54−57.
[2] 玛旦江·吐木尔, 王贻明, 吴爱祥, 等. 巴鲁巴铜矿节理裂隙调查及岩体质量评价[J]. 现代矿业, 2014, 30(10): 15−18. MA Danjiang·Tumuer, WANG Yiming, WU Aixiang, et al. Rock mass quality evaluation and survey on joints and fissures of Baluba Copper Mine[J]. Modern Mining, 2014, 30(10): 15−18.
[3] 李占炎. 巴鲁巴铜矿采矿方法的优化研究[J]. 矿业工程, 2011, 9(3): 27−29. LI Zhanyan. Optimizing study on the mining method in Baluba Copper Mine[J]. Mining Engineering, 2011, 9(3): 27−29.
[4] 王晶军. 巴鲁巴铜矿中央运输巷道变形机理及支护优化研究[J]. 矿冶, 2015, 24(2): 24−27. WANG Jingjun. Study on deformation mechanism and support optimization of Baluba Copper Mine's central tramming haulage[J]. Mining and Metallurgy, 2015, 24(2): 24−27.
[5] 何满潮, 景海河, 孙晓明. 软岩工程力学[M]. 北京: 科学出版社, 2002: 1−3.HE Manchao, JING Haihe, SUN Xiaoming. Soft rock engineering mechanics[M]. Beijing: Science Press, 2002: 1−3.
[6] 陈宗基. 地下巷道长期稳定性的力学问题[J]. 岩石力学与工程学报, 1982, 1(1): 1−20. TAN Tjongkie. The mechanical problems for the long-term stability of underground galleries[J]. Chinese Journal of Rock Mechanics and Engineering, 1982, 1(1): 1−20.
[7] 李学华, 杨宏敏, 刘汉喜, 等. 动压软岩巷道锚注加固机理与应用研究[J]. 采矿与安全工程学报, 2006, 23(2): 159−163. LI Xuehua, YANG Hongmin, LIU Hanxi, et al. Research on bolt grouting reinforcement technology in dynamic pressure and soft rock roadway[J]. Journal of Mining & Safety Engineering, 2006, 23(2): 159−163.
[8] 韩斌, 王贤来, 文有道. 不良岩体巷道的湿喷混凝土支护技术[J]. 中南大学学报(自然科学版), 2010, 41(6): 2381−2385. HAN Bin, WANG Xianlai, WEN Youdao. Drift support technology with wet shotcrete method in weak rock mass[J]. Journal of Central South University (Science and Technology), 2010, 41(6): 2381−2385.
[9] 何杰, 方新秋, 许伟, 等. 深井高应力破碎区巷道破坏机理及控制研究[J]. 采矿与安全工程学报, 2008, 25(4): 494−498. HE Jie, FANG Xinqiu, XU Wei, et al. Failure mechanism and control measures of roadway in high stress and broken area at a great depth[J]. Journal of Mining & Safety Engineering, 2008, 25(4): 494−498.
[10] LANA M S. Numerical modeling of failure mechanisms in phyllite mine slopes in Brazil[J]. International Journal of Mining Science and Technology, 2014, 24(6): 777−782.
[11] 方新秋, 赵俊杰, 洪木银. 深井破碎围岩巷道变形机理及控制研究[J]. 采矿与安全工程学报, 2012, 29(1): 1−7. FANG Xinqiu, ZHAO Junjie, HONG Muyin. Failure mechanism and control measure of roadway deformation with fractured surrounding rock in deep mine[J]. Journal of Mining & Safety Engineering, 2012, 29(1): 1−7.
[12] 姜耀东, 赵毅鑫, 刘文岗, 等. 深部开采中巷道底鼓问题的研究[J]. 岩石力学与工程学报, 2004, 23(14): 2396−2401. JIANG Yaodong, ZHAO Yixin, LIU Wengang, et al. Research on floor heave of roadway in deep mining[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(14): 2396−2401.
[13] SHARAN S K. Elastic-brittle-plastic analysis of circular openings in Hoek-Brown media[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(6): 817−824.
[14] BROWN E T, BRAY J W, LADANYI B, et al. Ground response curves for rock tunnels[J]. Journal of Geotechnical Engineering, 1983, 109(1): 15−39.
[15] SHARAN S K. Exact and approximate solutions for displacements around circular openings in elastic-brittle-plastic Hoek-Brown rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(4): 542−549.
[16] BRADY B, BROWN E T. Rock mechanics for underground mining[M]. London: Chapman and Hall, 2004: 166−168.
[17] 黄兴, 刘泉声, 乔正. 朱集矿深井软岩巷道大变形机制及其控制研究[J]. 岩土力学, 2012, 33(3): 827−834. HUANG Xing, LIU Quansheng, QIAO Zheng. Research on large deformation mechanism and control method of deep soft roadway in Zhuji coal mine[J]. Rock and Soil Mechanics, 2012, 33(3): 827−834.
(编辑 陈爱华)
Deformation mechanism and repair support of haulage roadway with weak-fractured surrounding rock
WU Aixiang1, HU Kaijian1, HUANG Mingqing1, WANG Yiming1, WANG Jingjun1, 2
(1. Key Laboratory of Ministry of Education for Efficient Mining and Safety of Metal Mines,University of Science and Technology Beijing, Beijing 100083, China;2. China Nonferrous Metal Mining (Group) Co., Ltd. Luanshya Copper Mines PLC, Beijing 100029, China)
To solve the support problem of soft-fractured surrounding rock underground, taking the haulage roadway of Baluba copper mine at 580 m level as study object. The stability of roadway was monitored, and the deformation characteristics of roadway and influencing factors were analyzed. The main influencing factors are stress concentration, weak and fractured surrounding rock, low supporting intensity and water. After analyzing the deformation mechanism of roadway, the mechanical model of roadway was established, based on the mechanical model and actual situation, the combined support design with “steel arch and long prestressed cable bolt” was put forward, and then the FLAC3D was used to analyze the stability of roadway before and after support. The results show that region of stress concentration is away from the roadway surface and the area of plastic zone of surrounding rock declined by 40%. The stability of roadway was monitored after repairing and the results indicated that the roadway deformation has been effectively controlled, with maximum subsidence 50 mm of the roof, maximum convergence deformation 39 mm of two side walls and no heaving floor in 60 d.
baluba copper mine; haulage roadway; weak-fractured surrounding rock; deformation mechanism; repair support; numerical simulation
10.11817/j.issn.1672−7207.2017.08.025
TD353
A
1672−7207(2017)08−2162−07
2016−09−10;
2016−12−25
国家“十二五”科技支撑计划项目(2012BAB08B02);国家自然科学基金资助项目(51304011,51374035)(Project(2012BAB08B02) supported by the National Key Technologies R&D Program during the 12th Five-year Plan; Projects(51304011, 51374035) supported by the National Natural Science Foundation of China)
黄明清,博士,从事溶浸采矿、充填采矿及岩石力学研究;E-mail:seango@126.com

