浅水调谐液体阻尼器阻尼力的模拟研究*
董 胜, 陈 更
(中国海洋大学工程学院, 山东 青岛 266100)
浅水调谐液体阻尼器阻尼力的模拟研究*
董 胜, 陈 更
(中国海洋大学工程学院, 山东 青岛 266100)
调谐液体阻尼器(TLD)是有效的结构减振装置。TLD在激励作用下内部液体运动属于晃荡问题。本文建立了求解二维不可压缩Navier-Stokes方程的数值模型。数值模型采用对时间积分的分步方法求解压力项,THINC格式捕捉自由面。利用晃荡试验数据验证了模型计算结果的正确性。模拟了不同深度的浅水TLD在不同频率激励作用下内部液体的运动,计算了TLD晃荡产生的阻尼力。分析激励频率对TLD中液体运动的形态和阻尼力的影响。浅水TLD中液体运动形态主要为行波。TLD产生的阻尼力受激励频率影响,在固有频率附近产生共振现象,阻尼力大,减振效果理想。
调谐液体阻尼器;晃荡;CIP;数值模拟
结构在工作环境中受到环境荷载的影响,产生振动。结构振动控制的概念由此产生。Yao[1]提出结构振动控制的概念,在此之后,这个领域持续发展成熟。结构振动控制装置不断发展,其中,被动吸能耗能装置调谐液体阻尼器(TLD)等得到了广泛的研究和应用。一般将液体深度与受激励方向尺寸之比小于1/8的TLD装置称为浅水TLD,反之称为深水TLD。浅水TLD工作频率范围宽,适用范围广,在工程实际中主要应用较多。
对TLD的研究主要集中在TLD-结构相互作用领域,特别是TLD对结构振动的减振效果及其优化设计有较多的成果。对TLD减振能力及内部液体晃荡现象的研究方法主要有数值模拟方法和试验方法。前者包括使用有限差分法或有限元法对矩形和圆柱形TLD的求解Navier-Stokes方程[2-4],从而得到TLD对结构的作用力(动水压力),其中文献[2]中利用VOF法得到了TLD动水压力的经验公式。试验方法有将TLD放置在振动台模拟受到激励后的响应[5],得到了模型试验中的附加阻尼力。本文中将TLD在工作时对支撑结构产生的反力统称为阻尼力,意义为TLD阻尼作用产生的力。TLD减振原理仍有待进一步研究,特别是TLD晃荡时液体运动形态和阻尼力之间的关系研究较少。内部液体运动形态对TLD减振有重要影响,对此研究有重要意义。
本文建立了求解Navier-Stokes方程的数值模型,利用THINC格式捕捉自由面,模拟TLD在工作时内部液体的运动情况,计算了TLD工作时产生的阻尼力。研究了激励频率对液体运动形态和阻尼力的影响。
1 数值模型
1.1 控制方程
二维不可压缩Navier-Stokes方程与连续方程分别为
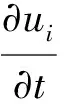
(1)

(2)



(3)
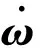
为了区分计算区域内的不同介质,如液体,气体和固体,引入体积函数φm=(1,2,3),满足方程:

(4)
(5)

边界条件要求容器壁为无滑移条件,因此,速度和压强的边界条件为
ur=0
,
(6)
(7)
式中:f即液体所受的体积力,包括重力。
TLD阻尼力在模型中为侧壁受到的压力差,文中取合力向右为正,向左为负。阻尼力计算公式为

(8)
式中:FTLD为阻尼力;Fright;Fleft分别为液体对计算域右侧和左侧产生的压力;p(i,j)为(i,j)处计算得到的压强;dyj为j处y方向网格间距。由此可得到TLD晃荡时产生的阻尼力。
1.2 CIP方法
CIP(Constrained Interpolation Profile)方法最早是由Takewaki等[6]提出的求解双曲型偏微分方程的方法。其原理是基于空间网格点的函数值及其空间导数,利用三次多项式插值近似,反演出网格单元内部变量的信息。下面以一维对流方程为例,简介CIP方法。

(9)
式中:f为函数曲线;u为常数;x为波传播方向。CIP采用一种独特的方式,在一个网格内建立了高阶差分格式。此法利用了网格点变量值以及空间导数值,描述并再现网格内的信息。
对方程(9)求空间导数,可得到
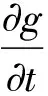
(10)
式中:g=∂f/∂x;对流速度u为常数;方程(10)右边项为零。不失一般性地假设u>0的情况,在迎风向单元[xi-1,xi]内n时刻剖面函数可以近似为

(11)
式中,aibicidi分别为待定系数。
在n+1时刻,单元格的剖面函数fn+1可以将n时刻的剖面函数fn平移-uΔt得到,函数f和g的时间演变可以通过拉格朗日变换得到

(12)
式中的4个未知系数2通过下式来确定
(13)
CIP方法在一个网格内实现了高阶差分格式,使得本文的数值模型可适用于复杂流动问题。
1.3 对时间积分的分步算法
求解Navier-Stokes方程采用分步算法(fractional step approach)对动量方程进行时间积分。计算分为两个过程:求解对流项和求解非对流项,后者又分为求解非对流步(I)和非对流步(II)。CIP方法被运用在求解对流项过程中,来求得预测值。计算每一步的过程分为,首先计算对流项,其次求解非对流项,然后求解压力方程,计算下一时间步压力,最后考虑压力梯度项,计算速度的最终值[7]。
1.4 自由面捕捉的THINC格式
计算域中的不同介质的确定是通过体积函数φm来确定的,在计算过程中每一步都需要确定自由面的位置来继续求解。Xiao[8]提出了THINC(Tangent Hyperbolic INterface Capturing)方法,用于捕捉不可压缩流体与气体之间的自由面。该方法属于VOF类方法,利用双曲正切函数来计算流体体积函数的数值通量。下面介绍一维THINC格式,多维计算可以通过方向分割方法得到。将体积函数(4)改写成守恒形式

(14)
与CIP格式使用三次多项式插值表示的形式不同,THINC格式利用双曲正切函数近似体积函数的分布。体积函数0≤φ≤1在自由面的变化两侧呈阶梯状,使用分段修正的双曲正切函数可以很好地模拟函数的变化。
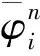
(15)
双曲正切函数非常简洁的拟合了体积函数阶梯形变化,使用分段修正的双曲正切函数表示
(16)
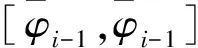
(17)
参数γ用来确定双曲正切函数的斜率方向,
(18)
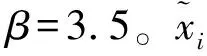
(19)
在所有的网格内计算出插值函数Fi(x)后,体积函数φ通过通量形式公式更新值
(20)
式中,gi+1/2表示网格边界x=xi+1/2上在时间[tn,tn+1]内的通量,式(14)在网格[xi-1/2,xi+1/2]和时间间隔[tn,tn+1]内进行积分得,计算公式为
(21)
一维THINC格式中的各变量如图1所示,阴影部分代表当ui+1/2≥0时gi+1/2的值。

图1 THINC格式示意图Fig.1 Concept of THINC scheme
2 模型验证
为了验证模型的正确性,模拟了Kishev[9]晃荡的物理模型试验,模型配置如图2。

图2 计算液舱尺寸及压力测点位置Fig.2 Sketch of tank and pressure points
装置宽60 cm,高30 cm,无内部结构。舱壁上有压力测点,位置如图2。液体深度h=12.0 cm,振幅5.0 cm,周期T=1.5 s。计算采用均匀网格,网格间距2~5 mm,计算总时长25 s,时间步长dt=2×10-4~6.25×10-4s。图3为dt=2×10-4s时,不同网格间距下计算得到的压力值。不同网格间距计算出的压力值与试验值相比非常接近。图4为网格间距为dx=dy=2 mm时,不同时间步长计算得到的压力值。可以看出,时间步长对计算结果影响较小。可以认为本文中的算法在模拟的时间步长和空间步长范围内计算结果稳定,对步长无依赖。在满足收敛性的条件下,可以用较大的网格密度和时间步长,来提高计算效率和经济性。

图3 不同网格密度计算的压力变化Fig.3 Pressure of different meshes

图4 不同时间步长计算的压力变化Fig.4 Pressure of diffrerent time steps
进一步考察单个周期内求解压力的准确性。图5为6.5~8 s内压力曲线。在压力第一个峰值处,计算值与实验值有不同程度的偏差。造成这个的原因有计算中气体和液体的交界面非常薄,可能仅跨几个网格,在非常短暂的时间内,压力从零到最大值,有一定数值的误差,需要进一步研究。在第一个峰值之后的各压力值是比较一致的。与实验结果相比,总体趋势较吻合,在最后一个峰值稍有低估。

图5 一个周期内的压力曲线Fig.5 Pressure profile in one period
3 TLD阻尼力计算
利用已建立的数值模型计算TLD在简谐运动下产生的阻尼力。假设TLD尺寸宽为B,高为H,液体深度为h,根据线性理论,固有频率为

(22)
n=1时,为第一阶固有频率,它是非常重要的参数,TLD应用时常将其第一阶固有频率调谐至结构受到主要激励的频率附近,使TLD能够产生共振现象,剧烈的晃荡将耗散动能,起到减振的效果。
计算选取尺寸为H=1 m,B=1 m的TLD,浅水条件下水深不超过12.5 cm,分别选取水深为5,8和12 cm三种深度计算。根据式(22)可知,三种情况下第一阶固有频率ω1分别为2.19、2.75、3.30 rad/s。在一阶固有频率附近分别施加激励,模拟TLD中液体运动状况。激励频率变化范围ω/ω1=0.8~1.4。激励幅度为ηA=5 cm。激励的运动规律服从简谐运动:x=-ηAcos(ωt+φ0)。计算不同激励频率以及液体深度下TLD内液体运动形态和TLD阻尼力的变化。浅水情况下不同计算工况如表1。

表1 浅水TLD计算工况Table 1 Simulation cases of shallow water TLD
3.1 浅水TLD液体运动形态
在浅水条件下,TLD中的液体运动主要表现为行波。如图6为Case1ω/ω1=0.8时液体运动的形态。液体中的行波由左向右运动,水深较浅,波面产生破碎,破碎后卷入空气,剧烈的掺混造成能量耗散。液体在继续向右运动后,触及右侧壁面后,向上继续运动,动能转化为势能,对侧壁的压强增大,与左侧产生压力差,作用在TLD侧壁上,TLD整体受到向右的压力,此即为阻尼力产生的机理。
图6~8为Case1相同深度下,不同激励频率下波峰触及右侧壁时的的运动瞬间。从形态上看,频率越大,TLD内的液体运动越剧烈。

图6 Case1 ω/ω1=0.8水体运动瞬间Fig.6 Snapshots of Case1 ω/ω1=0.8
图7为Case1ω/ω1=1.0时液体运动的瞬间。与图6相比,激励频率变大,产生的行波运动更快,更容易破碎,因而具有更好的能量耗散的效果。

图7 Case1 ω/ω1=1.0水体运动瞬间Fig.7 Snapshots of Case1 ω/ω1=1.0
图 8为Case1ω/ω1=1.4时不同时刻液体运动的瞬间。相比图6和7,流体运动更加剧烈。

图8 Case1 ω/ω1=1.4水体运动瞬间Fig.8 Snapshots of Case1 ω/ω1=1.4
图 9为Case2ω/ω1=0.8时水体运动瞬间,相比图7,可以看出,由于水深增加,行波并未破碎。图10和11比较可知,随着频率的增加,TLD内液体的晃荡现象更加剧烈。由此可知,激励频率的变化对TLD内液体运动的形态有很大影响。相同尺寸和激励幅度下,激励频率小于TLD固有频率时,波浪尚未破碎,而当激励频率在TLD固有频率附近时,内部液体的剧烈运动,波面发生破碎。

图9 Case2 ω/ω1=0.8水体运动瞬间Fig.9 Snapshots of Case2 ω/ω1=0.8
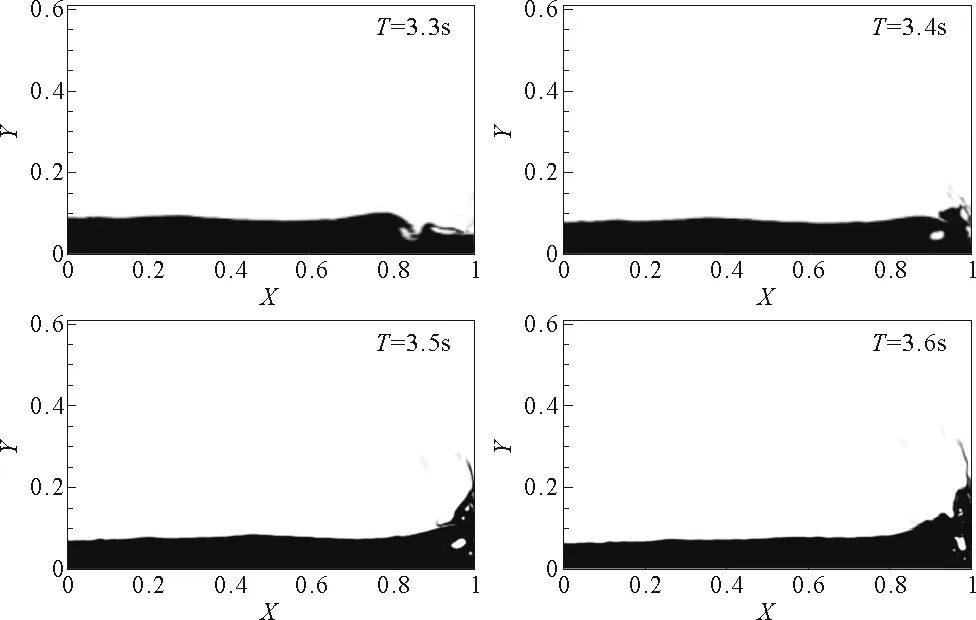
图10 Case2 ω/ω1=1.0水体运动瞬间Fig.10 Snapshots of Case2 ω/ω1=1.0
图 12为Case3ω/ω1=0.8时不同时刻液体运动的形态。与图6和9相比,由于水深进一步增加,液体的运动更加平稳。图13中可观察到,激励频率增大到固有频率附近后,波浪破碎现象继续出现。图14为Case3ω/ω1=1.4时不同时刻液体运动的形态,当激励频率继续增加,可见波浪破碎的现象反而有所减轻。

图12 Case3 ω/ω1=0.8水体运动瞬间Fig.12 Snapshots of Case3 ω/ω1=0.8

图13 Case3 ω/ω1=1.0水体运动瞬间Fig.13 Snapshots of Case3 ω/ω1=1.0

图14 Case3ω/ω1=1.4水体运动瞬间Fig.14 Snapshots of Case3 ω/ω1=1.4
浅水TLD当水深较小时,液体运动受到非线性作用。TLD内液体的运动形态为行波。行波在触及侧壁前就破碎,形态为卷破波,此时破碎对能量耗散有利,但破波的位置远离侧壁。当激励频率增加至与固有频率附近时,会发生共振现象。行波在侧壁处破碎,能够产生较大的冲击力。当激励频率大小超过TLD的固有频率后,流体运动形态变得非常不规则,波面破碎位置不确定。水深增加,特别是当水深临近TLD浅水的1/8界限时,在远离固有频率时波浪反而难以破碎,对于减振效果并无益处。
3.2 浅水TLD阻尼力
本节分析不同激励条件和水深情况下,TLD产生的阻尼力的变化情况。图15~17分别为Case1,Case2和Case3,ω/ω1=0.8,1.0,1.4时TLD产生的阻尼力随时间变化曲线。由于液体运动非常激烈,计算值为虚线,同时加入移动平均得到的平滑值,以显示曲线趋势。
图15~17中可以看出,当ω/ω1=1.0时,TLD产生的阻尼力在共振现象影响下,峰值很快达到了稳定,峰值大小大于远离固有频率激励下产生的阻尼力。图16(c)中某些时刻阻尼力的峰值是大于(c)中的峰值的,但是总体来说,仍可以认为ω/ω1=1.0时的性能是优于其他情况的。在激励频率靠近固有频率时是TLD最理想的工作状态。当ω/ω1=0.8时,三种深度下的TLD产生的阻尼力都较小。当ω/ω1=1.4时,阻尼力的峰值和ω/ω1=1.0时的阻尼力的峰值接近,但峰值大小波动性较大,不如ω/ω1=1.0时稳定。

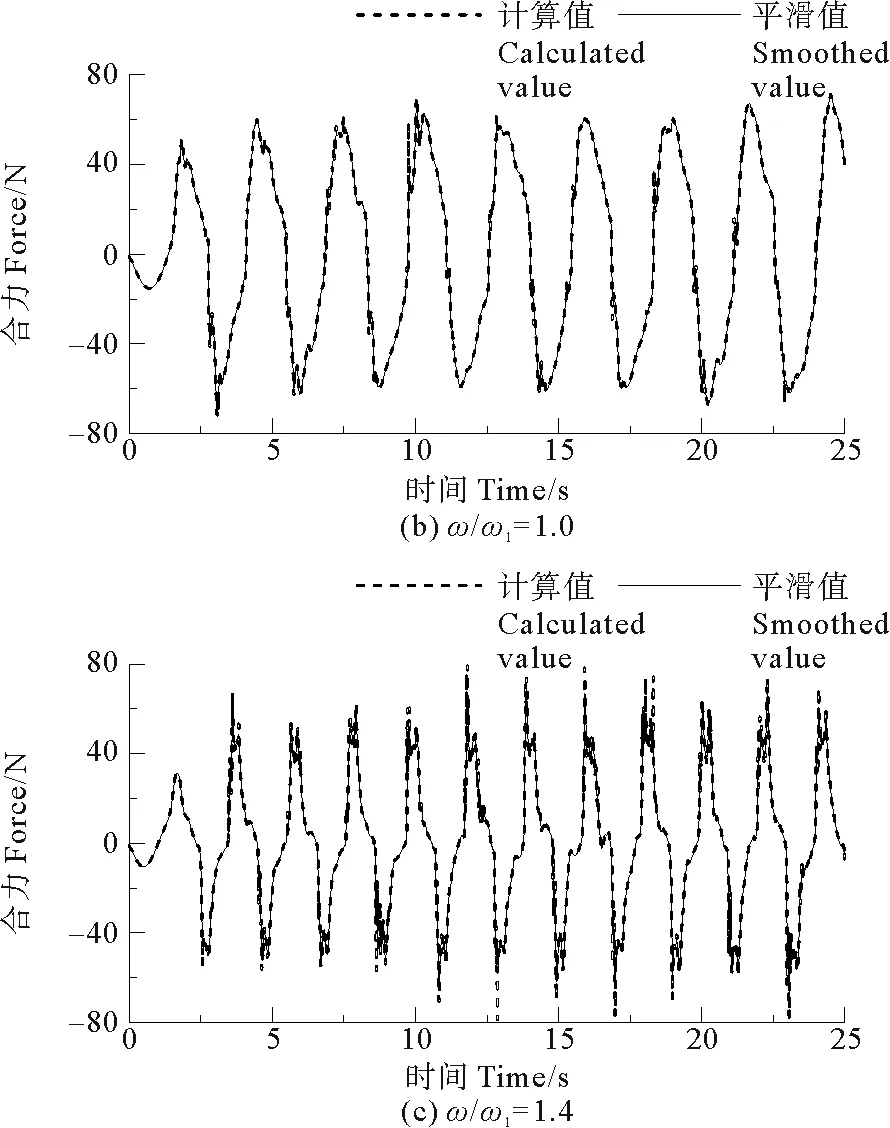
图15 Case1的阻尼力Fig.15 Damping force of Case1

图16 Case2产生的阻尼力Fig.16 Damping force of Case2

图17 Case3产生的阻尼力Fig.17 Damping force of Case3
综合计算结果,得到图18不同深度阻尼力峰值大小随频率变化曲线。可以看出激励的频率对TLD阻尼力有较大影响。不同深度下阻尼力峰值最大值均出现在ω/ω1=1.0时。

图18 不同深度阻尼力峰值随频率变化曲线Fig.18 Damping force of different depth
在水深较浅的Case1中,TLD阻尼力由于浅水的非线性造成的波浪破碎和与气体的掺混,使得计算的阻尼力波动较大,由图15(a)可见,压力的时间序列中若干小峰值,主要是在波面卷破时,数值模型未考虑气体的可压缩性,对结果有一定影响。当ω/ω1<1.0时阻尼力峰值随着激励频率变大而增加,在ω/ω1=1.0时,阻尼力达到最大。当ω/ω1>1.0时,阻尼力峰值大小随着激励频率增大而减小并趋于稳定。
在水深接近1/8的临界点的Case3中,ω/ω1<1.0时,阻尼力的峰值大小随着激励频率增加而增加,在超过ω/ω1=1.0后峰值逐渐减小。
而水深介于Case1和Case3之间的Case2,阻尼力的峰值最大值同样出现在ω/ω1=1.0处。当ω/ω1<1.0时,阻尼力随着频率增大而增大,在ω/ω1>1.0后,阻尼力的峰值逐渐变小。
本节利用数值模型计算分析了不同深度的浅水TLD的液体运动形态和阻尼力在不同激励频率下的变化。浅水TLD受到的激励的频率越靠近TLD的固有频率时,阻尼力越大,减振效果越好。
4 结论
(1)浅水TLD在受到激励后,内部液体运动形态为行波,当水深较浅时会发生波面的破碎,水深较深时,行波破碎现象在靠近固有频率时才会发生。
(2)激励的频率对浅水TLD的减振效果影响较大,当频率靠近TLD的固有频率时,会产生共振现象,液体运动激烈,产生的阻尼力大,并且存在波面的破碎,耗散了动能。
(3)浅水TLD内部液体的深度对TLD减振效果有非常重要的影响,水深较浅的TLD的液体运动剧烈,减振效果更好。
[1] Yao J T. Concept of structural control[J]. Journal of the Structural Division, 1972, 98(7): 1567-1574.
[2] 贾影, 李宏男, 李玉成. 调液阻尼器液体动水压力的模拟[J]. 地震工程与工程振动, 1998, 18(3): 83-88.
Jia Ying, Li Hong-nan, Li Yu-cheng. Simulation of dynamic liquid pressure for tuned liquid damper[J]. Earthquake Engineering and Engineering Vibration, 1998, 18(3): 83-88.
[3] 李书进, 李桂青. 结构控制中圆柱形浅水TLD的研究[J]. 特种结构, 2000, 17(4): 45-48
Li Shu-jin, Li Gui-qing. Research of shallow water TLD in vibration control[J]. Special Structures, 2000, 17(4): 45-48.
[4] 岳宝增, 刘延柱, 王照林. 非线性流固耦合问题的ALE分步有限元数值方法[J]. 力学季刊, 2001, 22(1): 34-39.
Yue Bao-zeng, Liu Yan-lin, Wang Zhao-lin. ALE fractional step finite element method for fluid-structure nonlinear interaction problems[J]. Chinese Quarterly of Mechanics, 2001, 22(1): 34-39.
[5] 岳前进, 张力, 刘小惠, 等. 调谐液体阻尼器(TLD)附加阻尼力的量测[J]. 土木工程学报, 2008, 41(6): 22-26.
Yue Qian-jin, Zhang Li, Liu Xiao-hui, et al. Measurement of the supplementary damping force of tuned liquid dampers[J]. China Civil Engineering Journal, 2008, 41(6): 22-26.
[6] Takewaki H, Nishiguchi A, Yabe T. Cubic interpolated pseudo-particle method (CIP) for solving hyperbolic-type equations[J]. Journal of Computational Physics, 1985, 61(2): 261-268.
[7] Zhu X. Application of the CIP method to strongly nonlinear wave-body interaction problems[D]. Trondheim: Norwegian University of Science and Technology, 2006: 25-28.
[8] Xiao F, Honma Y, Kono T. A simple algebraic interface capturing scheme using hyperbolic tangent function[J]. International Journal for Numerical Methods in Fluids, 2005, 48(9): 1023-1040.
[9] Kishev Z R, Hu C H, Kashiwagi M. Numerical simulation of violent sloshing by a CIP-based method[J]. Journal of Marine Science and Technology, 2006, 11(2): 111-122.
SimulationofDampingForceofTunedLiquidDamperwithShallowWater
DONG Sheng, CHEN Geng
(College of Engineering, Ocean University of China, Qingdao 266100, China)
Tuned liquid damper (TLD) is an effective equipment for structural vibration control and is applied in different areas. To study and maximize the effect of TLD vibration control, the mechanics of TLD is of great significance. The reaction of liquid in TLD is a sloshing problem. Sloshing is the liquid movement in a limited space (tank) and interaction with the container. The reaction of liquid in the tank is dynamic pressure due to liquid movement. The dynamic pressure is called damping force, which is the main factor of TLD vibration control. To calculate the damping force of TLD, computational fluid dynamics model is set up. The model is based on finite difference method to solve the two-dimensional incompressible Navier-Stokes equation. The Constrained Interpolation Profile (CIP) method is used in fractional step approach to solving pressure term and Tangent Hyperbolic Interface Capture (THINC) scheme, which is accurate and needs no geometry reconstruction, is employed to determine free surface location. The numerical model is validated by sloshing simulation compared with experiment data. The result shows good agreement with experiment data and the model is efficient and could simulate pressure accurately. The damping force is calculated by liquid pressure exerted on tanks.
Different cases are simulated to study the effect of water depth and the excitation frequency of TLD. The TLD is under the harmonic excitations. Three different water depths are considered and every different depth cases are tested under seven excitation frequencies from 0. 8ω1to 1. 4ω1.ω1is the natural frequency of TLD. Results show that traveling-wave is the main form of liquid moves in TLD under external excitations. Waves break when the water is shallow and excitation is near the natural frequency. The frequency of excitation has great influence on the damping effect of TLD. When the frequency is close to the natural frequency of TLD, the resonance phenomenon occurs, and the motion of the liquid is intense, the damping force is large, and the wave front is broken. Kinetic energy is dissipated violently, which enhance the effectiveness of structural vibration control. The shallow internal liquid depth of TLD has an impact on vibration control, in which liquid movement is intense and dissipate more kinetic energy.
Tuned liquid damper(TLD); sloshing; Constrained Interpolation Profile(CIP); numerical simulation
O353
A
1672-5174(2017)12-110-08
责任编辑 陈呈超
10.16441/j.cnki.hdxb.20150158
董胜, 陈更. 浅水调谐液体阻尼器阻尼力的模拟研究[J]. 中国海洋大学学报(自然科学版), 2017, 47(12): 110-117.
DONG Sheng, CHEN Geng. Simulation of damping force of tuned liquid damper with shallow water[J]. Periodical of Ocean University of China, 2017, 47(12): 110-117.
国家自然科学基金项目(51479183)资助
Supported by Natural Science Foundation of China(51479183)
2015-04-12;
2017-01-12
董 胜(1968-),男,教授,博导。E-mail:dongsh@ouc.edu.cn

