基于信息熵的手机游戏主界面设计的质量评价

林泓羽　张宇红

摘要：对手机游戏的界面设计进行质量评价，首先根据需要，利用层次分析法可以将众多评价指标划分为三大类：技术型指标，功能型指标，情感型指标，将这些指标结合起来就组成了多属性的综合评价指标体系。对不同的定性与定量指标进行归一化处理，可以构建起规范化的评价矩阵，可以此为基础进行设计质量评价的线性规划。引入信息熵概念来描述评价指标权重以及线性规划系数所具有的不确定性，同时线性规划的最优解问题也可以通过最大熵原理求得。通过实际案例，代入评价小组的评价数据，筛选出最优设计方案。

关键词：信息熵 界面设计 质量评价 不确定性

中圖分类号：TB47 文献标识码：A

文章编号：1003-0069（2017）04-0057-03

引言

对手机游戏主界面的设计方案进行质量评价，一方面可以验证方案是否达到了设计目的，避免出现开发资源的浪费；另一方面，在进行竞品分析或是方案选择时，可以指导和帮助我们进行正确的决策。对于设计方案质量评价的结果，主要由以下三个影响因素决定：质量评价方法，评价指标权重，评价矩阵。

当前，针对某方案的质量评价方法主要有统计分析评价法、模糊评价法、相关图分析法、层次分析法等；在质量评价中对于评价指标权重的确立，则主要采用AHP层次分析法，Delphi专家赋权法，变异系数法等；就目前而言，若要构建一个评价矩阵，大多采用专家直接主观赋权的方法，来确立评价指标的权重以及评价矩阵中涉及到的系数。

然而手机游戏的主界面设计，具有多维度、多属性、高耦合等特点，这就意味着对于其设计质量评价的过程需要考虑到众多纷繁复杂的影响因素，而这些影响因素则会给各项评价指标的权重以及评价矩阵的系数带来不同程度的不确定性。因此，如果要从更加客观的角度对手机游戏主界面设计方案进行质量评价，其过程中所涉及到的不确定性是不容忽视的。我们可以通过信息熵的概念将评价过程中的不确定性进行准确的描述，以此确保对设计方案质量评价的客观性，并以此筛选出最佳的游戏主界面设计方案。

一、评价指标体系的建立

（一）指标层次分析

要对设计方案进行质量评价，首先需要根据目标筛选出不同的评价指标，并以此为建立起多属性，多维度的评价指标体系。首先可以利用层次分析的思想，将手机游戏主界面设计的质量评价指标划分为技术型指标、功能型指标以及情感型指标三个层次。因为评价体系的建立既要考虑界面本身的可操作等功能性因素，同时也要考虑对玩家需求的满足程度以及带给玩家的情感体验。可以将手机游戏主界面设计的质量评价指标体系，进行如下层次结构分类：

设集合A（界面设计综合质量指标）={A1（技术指标），A2（功能指标），A3（情感指标））

其中，A1（技术指标）=（信息容量，可视范围，操作范围，隐藏范围，图标数量，颜色种类，视觉平衡，可视性，简洁性…）

A2（功能指标）={功能数量，操作准确率，操作步奏，便捷性，反馈时间，功能指导性，一致性，交互方式…}

A3（，情感指标）={视觉代入感，听觉代入感，愉悦感，烦躁感，进步感，挫败感…）

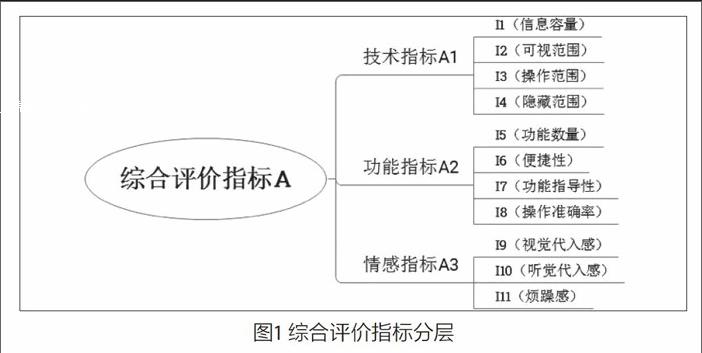
根据游戏种类，设计阶段，评价目的等因素不同，可以根据需要，对相应的评价指标进行进一步的细分优化，构建起多层次结构的评价指标体系。以武侠类大型多人在线手机游戏为例，建立如下图所示质量评价指标体系（图1）：

（二）体系中的符号定义

假设现在对n个界面设计方案进行质量评价，记为P_D={P_D1，P_D2，P_D2，P_Dn}；评价指标数量为m，记为I_C={I_C1，I_C2，I_C3，…，I_Cm）。方案P_Di对第j个指标I_Cj的设计值用C_ij表示，其中（I=1，2，3，n；J=1，2，3…m），那么n个设计方案会存在有mn个设计值，用矩阵P_M=[C_ij]nxm来表示，可以称其为相应的设计矩阵。而评价方案对第j个指标I_Cj的评价值用R_Cj。表示，其中（I=1，2，3，n；J=1，2，3…m），那么n个设计方案的会存在mn个评价值，用矩阵R_D=[R_ij]nxm来表示，可以称其为相应的评价矩阵。如果有多个专家或是质量评价小组，采用一种或是多种方法对于设计方案进行质量评价，那么将得到多种评价结果，设有h种，对于某个设计方案的评价矩阵就可以记为A¹，A²，…，A^k，…，A^h。

二、质量评价的线性规划

（一）评价指标规范化

由于不同评价指标之间的量纲不统一，将无法直接用于比较或是计算。所以如果要进行一个涵盖众多指标综合性评价，就必须对各项评指标进行归一化处理，消除量纲不同带来的影响，得到规范化的评价矩阵。对于一些定性指标I_Cj例如便捷性，代入感等，本文采用5级分值标度处理，用很好、好、中、较差、差，评分采用0-1分制原则，通过简单加权法，可以表示关于某个定性指标的评价值R_Cj（图2）；

对于一些定量指标I_Cj，如果其值越大越好，例如像操作准确率，设计方案集P_D的设计值集X={x₁，x₂，x₃，…，x_n}，则令R_ij=（x_i-min x_i）/（max x_i-min x_i）；endprint

若其目标越小越好，例如像反馈时间，则令R_ij=（max x_i-x_i）/（max x_i-min x_i），0≤R_ij≤1。这样处理就能消除指标之间量纲不同带来问题，得到规范化的评价值，从而建立起规范化的评价矩阵R_D。

（二）线性规划处理

因为有多个评价小组或者是专家对于一个设计方案进行评价，所以将得到评价结果A^k。因此可以将评价结果进行线性组合表示：

d_i小，则可以认为该方案接近于理想方案；反之，则认为该方案并不理想方案，或者说与理想方案存在一定差距。然而理想方案是未知的，所以如果要从待评价方案中，选取一个最佳方案，就需要对线性组合的评价矩阵进行线性规划，以求得最优解。

（三）系数的不确定性

实际上（2）式中出现的线性组合系数λ_k是一个随机变量，会因具体情况而改变。实际上，此时的评价矩阵是一个随机矩阵，其结果会因λ_k改变而变化。而（4）中的R^k_ij可以理解为评价指标中的第k个样本值，在满足式（2）的条件下，R^k_ij的线性组合系数λ_k可以看作是评价指标的概率分布。因而可见，线性组合系数是具有不确定性的。

（四）权重的不确定性

在对一个游戏界面设计方案的质量评价中，各项评价指标所占的权重w_j主要由以下几个因素决定：玩家需求程度，指标之间的相互关联程度，以及设计方案的之间的竞争性影响等。

1.指标与玩家需求影响

玩家的需求会对评价矩阵的最终结果造成很大影响。由于玩家的性别、年龄、层次、教育水平，游戏经验，性格偏好等都不相同，有的玩家更重视画面效果，有的玩家更重视操作体验，有的玩家更重视社交互动效果。所以不同玩家具有不同需求，他们对于各项指标的重视程度是不一样，那么对于同一指标的评价值则很有可能大相径庭。因此玩家需求的不确定性，导致了各项评价指标权重具有不确定性。

2.指标之间的相关关系影响

当某一项指标改变，引起了另—项指标值的变化时，就说明这两个指标之间存在相关关系。指标之间的相关关系既有正相关关系，例如当操作步奏增加时，烦躁感可能会增加；也有负相关关系，例如当手机游戏主界面中的操作范围增大时，其可视范围可能会减小。正是因为指标之间存在着这种动态变化的相关关系，使得指标权重具有不确定性。

3.设计方案的竞争性影响

手机游戏与其他互联网产品不同的是，其本身具有明显的竞争性和时间上的互斥性，用户可以一边用手机听音乐一边看新闻，却不能在同一时间内玩两个手机游戏。并且一般而言，玩家选择了某款游戏并投入了时间和精力之后，由于玩家的沉默成本，在一段时间之内往往都不会再选择同类型的竞争游戏。因此就所有的待评价设计方案而言，评价指标值很大程度上就会受到相互竞争的游戏的影响。例如一个玩家在玩了一段时间界面信息容量较小，但隐藏范围较大的游戏之后，让其评价一个界面信息容量大但操作步奏少的游戏，玩家就可能觉得不适应并觉得繁杂产生厌烦感。因此，游戏设计方案之间存在的竞争性影响关系，使得指标权重具有不确定性。

假设w_j是关于玩家需求，指标间相关关系，设计方案竞争性的概率密度函数，有

式中，x₁代表玩家需求因素，x₂代表指标间相关关系因素，x₃代表设计方案竞争性因素。在一定的边界条件下，能够解得最优解w_j，使得趋近于指标的理想权重w^*_j。

（五）信息熵

信息熵通常用来描述信息的不确定性，我们可以将线性组合系数和指标权重看作两个不确定事件，因其具有不确定性，可以用信息熵公式将其表述：

至此，基于信息熵的游戏主界面设计的质量评价工作，就可以转化成一个多目标的线性优化问题，并且可以用拉格朗日函数对此加以表述。

三、质量评价优化

四、案例研究

我们选择近期比较受欢迎的4款武侠类大型多人在线手机游戲的主界面设计进行分析，《剑侠世界》《剑侠情缘》《诛仙》《天下》（图3）：

（表1）所示为4个游戏的主界面设计方案的各项设计值，将（表1）按照中各项指标的设计值进行规范化处理后，可以得到如（表2）所示的界面设计的质量评价矩阵。选择4个质量评价小组分别对4个游戏的主界面设计方案进行质量评价，并对指标进行规范化处理，可以得到如（表3）所示的综合型质量评价矩阵。

解式（16）可知，当λ_k（k=1，2，3，4）最逼近λ时，则λ对应的界面设计方案就是最佳设计方案。由计算可知第1组的λ₁最接近λ，因此最佳的主界面设计方案应该是《剑侠世界》。

结论

（一）通过层次分析法可以将手机游戏的主界面设计的指标分为技术型指标，功能型指标和情感型指标三个层次。我们可以针对其他不同类型的游戏，或者是不同界面的设计，根据不同评价需求，对指标分层进行进一步的细化调整。

（二）由于评价指标与玩家的需求关系不同，指标之间的相关关系影响，以及设计方案的竞争关系等因素，为指标的权重以及评价过程中的线性规划系数带来了不确定性。而这些不确定性可以被信息熵的概念和公式客观描述。同时，线性规划中的优化问题，也可以利用最大信息熵原理加以解决。

（三）利用线性优化，构造拉格朗日函数求解多目标优化问题，从更为客观方向对游戏界面设计的质量进行评价研究，这样的方法对于指导开发游戏和进行方案决策时会更加有效。endprint