改进的GrabCut算法木材表面缺陷图像分割试验1)

白雪冰 宋恩来 李润佳 许景涛

(东北林业大学，哈尔滨，150040)

改进的GrabCut算法木材表面缺陷图像分割试验1)

白雪冰 宋恩来 李润佳 许景涛

(东北林业大学，哈尔滨，150040)

试验采用传统GrabCut算法和改进的GrabCut算法，针对单目标、多目标、复杂背景下多目标的木材表面缺陷图像进行多组对比实验。结果表明：改进后的GrabCut算法，针对木材表面的缺陷图像分割进行了优化，能有效改进传统GrabCut算法中的欠分割和过分割、易受区域凹凸纹理的干扰等缺点，而且分割各类木材表面缺陷图像时都能取得较好的效果。说明改进后的GrabCut算法具有其优势和可行性。

木材表面缺陷；木材图像分割；GrabCut算法

目前传统的木材表面缺陷分割方法有边缘检测、阈值法和区域分割。边缘检测算法，是以图像的像素在其邻域内灰度的变化为依据[1]，检测像素及邻域的灰度变化。该分割方法可以把木材表面缺陷边缘检测出来，但对于含有较细密木材纹理的图像分割结果中存在过多的伪边缘，受到噪声影响较大，分割出来的缺陷区域轮廓不清晰、效果不理想。阈值法，属于图像区域分割算法，通过不同特征阈值划分图像像素所属区域，完成分割。该方法对于背景平滑的虫眼和活节图像能得到较好的分割结果，但对含有较多纹理背景的死节缺陷图像难以得到满意的缺陷边界，并且难以区分分割结果中缺陷区域和背景区域。区域分裂对图像进行区域划分，使得初始区域互不相交，按照均匀性准则进行分裂与合并，直到划分出的均匀区域数量达到最小为止，但是合并的分割结果存在较多伪边界方块，区域生长的分割结果存在局部过分割或欠分割现象。针对传统木材图像缺陷分割方法存在的不足，本文提出了改进的Grabcut算法，旨在为拓展木材表面缺陷图像分割质量提供参考。

目前，在图像预处理领域中，过分割预处理方法已经日趋成熟[2]。过分割能够减少图像冗余，降低图像后处理的复杂度，简化了图像局部特征的计算。通过一定准则，可将相似度高且空间相邻的一些像素归类到一起。Ren等根据他们的分类模型，最早提出了超像素这一概念。基于图论的超像素分割方法，把图片映射成网络图，图片的像素对应网络图中的节点，相邻像素的关系对应网络图的边，相邻像素间的差异或相似程度对应边上的容量，按照一定准则对网络图进行分割，实现超像素图构建[3]。由于基于图论的超像素构建方法的目标性高，但计算量和计算复杂度较高，因此，文中选择基于梯度上升/下降的超像素构建方法进行图像的过分割处理。

1 试验材料

试验用的木材缺陷原图像，选自自建的木材缺陷图像库，缺陷种类包括活节、虫眼和死节。

2 超像素算法的比较

采用简单线性迭代聚类(SLIC)算法、改进的线性聚类(SLICO)算法2种过分割算法对图1中的单目标图像(512×512)进行图像分割试验。由图2～图4可见：SLIC和SLICO算法能够得到较为规则的超像素块，且以上所有SLIC和SLICO算法的超像素图中像素个数均为200个，处理时间分别为0.310 9、0.307 6 s。SLIC算法在缺陷边界处纹理明显的地方，存在少量不规则超像素块，而SLICO的超像素图中的超像素块均较为规整。

图1 木材表面缺陷原图像

图2 活节缺陷图像超像素图像

图3 虫眼缺陷图像超像素图像

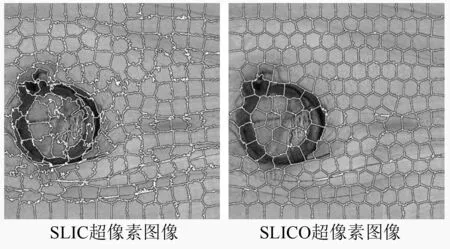
图4 死节缺陷图像超像素图像

为了进一步验证SLICO算法的优越性，对SLIC算法和SLICO算法通过设置不同超像素个数和聚类紧密度进行试验分析。试验在原图像(见图1)基础上，设置SLIC算法和SLICO算法的超像素个数为100、600、1 000进行试验(见图5～图7)。图5～图7中，SLIC算法和SLICO算法100个超像素所用的时间分别为0.223 4、0.217 3 s，600个超像素所用的时间分别为0.513 3、0.500 4 s，1 000个超像素所用的时间分别为0.882 4、0.870 4 s。综合考虑保留有效边界的能力以及运行的时间，选定600个超像素块的超像素图像进行改进GrabCut试验。

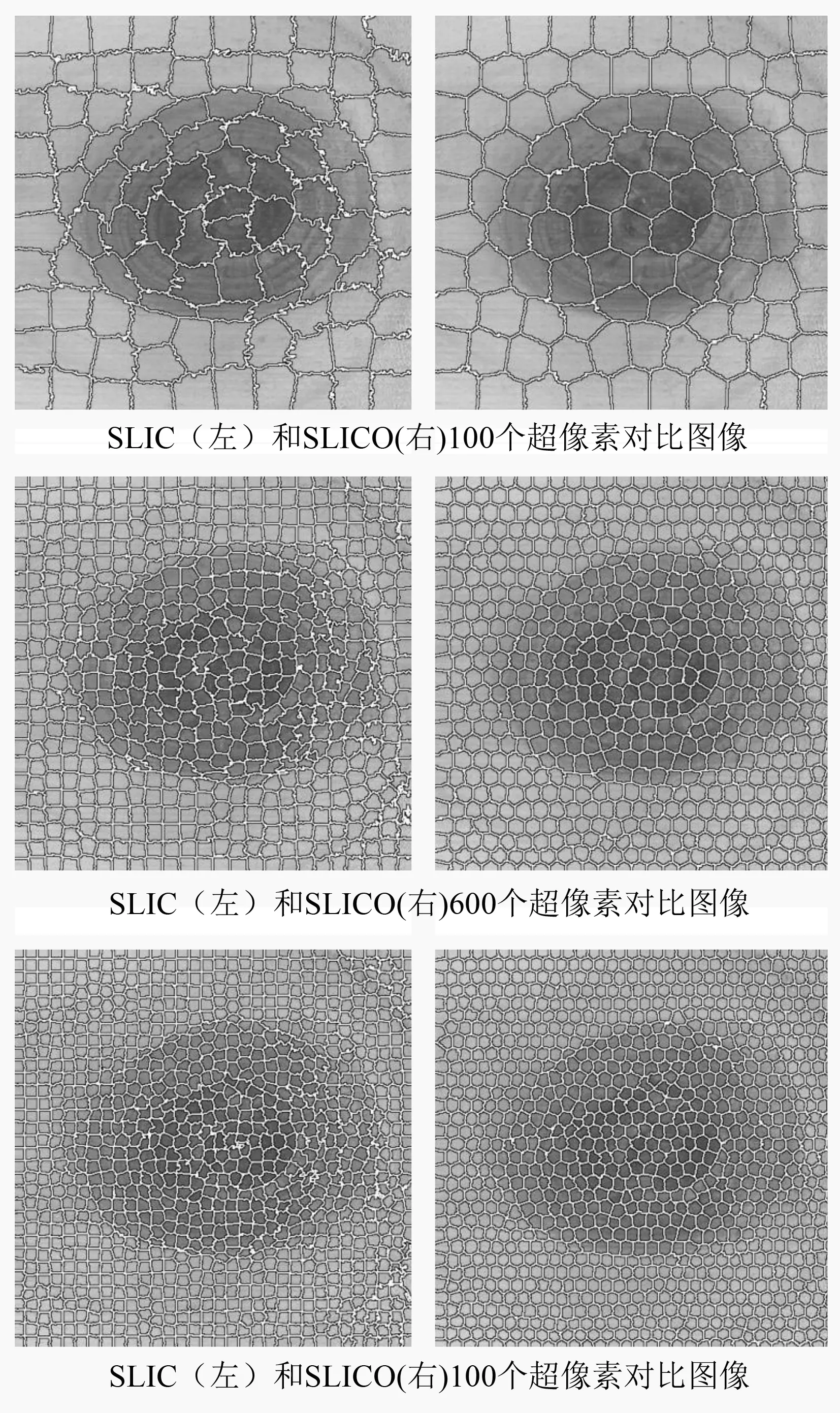
图5 活节不同像素的超像素对比图像

3 改进的GrabCut算法试验

3.1 改进的GrabCut算法的原理

GrabCut算法是Rother等人在Boykov等提出的基本图割框架上进行改进得到的。该算法具有如下3个特点：①使用高斯混合模型(GMM模型)取代灰度直方图表达颜色信息的概率分布的方法，实现将灰度图像分割延伸到彩色图像分割；②在GMM模型参数学习中，使用可进化的迭代算法代替一次最小估计，从而使能量最小化，最终提升了分割的精确度[4]；③通过非完全标号方式进行标记，从而减少操作者交互的时间，用户只要围绕目标圈定一个矩形框即可[5]。

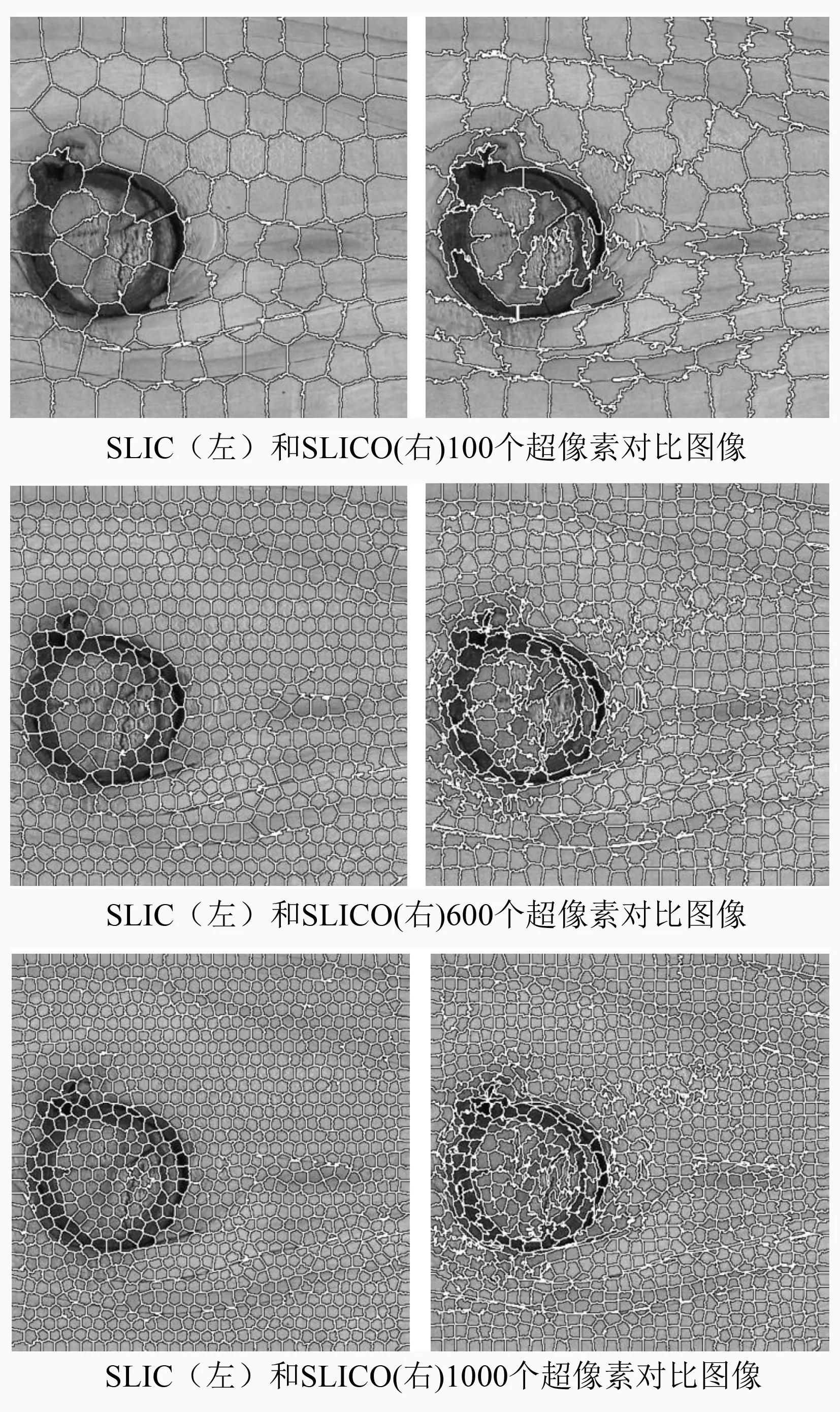
图7 虫眼不同像素的超像素对比图像

综上所述，GrabCut算法利用对彩色图像的GMM，表示目标与背景的像素点的分布，针对彩色图像中各个像素点的通道用GMM建立模型，再利用迭代算法最小化能量函数，最后运用非完全标号(IL)的方式降低交互过程花费的时间。

GrabCut算法将图像表示为矢量Z={z1，z2，…，zn，…，zN}，将该图像的分割表示为求每个像素点的值α={α1，α2，…，αn，…，αN}(其中αn∈[0，1])，因而αn只能去0(背景)或者1(目标)。图像目标与背景模型的建立，分别用k维(通常k=5，即目标和背景分别为5个高斯组件)的全协方差GMM，其中，向量K={k1，k2，…，kn，…，kN}作为每个像素的独立GMM(目标或背景)的参数，参数来自目标还是背景取决于αn的值[6]。从而把目标提取的问题变为最优能量函数的问题，再通过图割方式解决。

对于RGB空间上的彩色图像，GrabCut用来分割的吉布斯能量函数的形式为：

E(α，k，θ，z)=U(α，k，θ，z)+V(α，z)。

(1)

式中：E为Gibbs能量；U为数据项；V为光滑项；α为不透明度(且α∈[0，1]，0为背景，1为目标)；θ为图像目标和背景的灰度直方图；z为图像灰度值数值。

数据项U定义为：

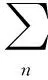
(2)

D(αn，kn，θ，zn)=-logp(zn|αn，kn，θ)+

logπ(αn，kn)。

(3)

式中：π(αn，kn)为此高斯模型样本数占总体的混合权重系数；p(zn|αn，kn，θ)为高斯概率分布。因此数据项也可以表示为：

D(αn，kn，θ，zn)=-logπ(αn，kn)+(1/2)logdet∑(α，k)+(1/2)[zn-μ(αn，kn)]T∑(αn，kn)-1[zn-μ(αn，kn)]。

(4)

则得，高斯混合模型的参数模型为[7]：

θ={π(α，k)，μ(α，k)，∑(α，k)}。

(5)

式中：π(α，k)为高斯概率分布的样本占总数的权值；μ(α，k)为高斯模型的均值；∑(α，k)为协方差；α为不透明度Alpha值，α=0、1；k为高斯混合模型参数，k=1、…、K。

平滑项V可采用RGB空间的欧几里德距离求得：

(6)

式中：C为成对相邻像素对；γ为自适应λ参数；β为常数项。

若某一个像素点被定义了另外一个更精确的标记，则会惩罚更小的数据，使总能量函数减小，迭代、收敛直到达到最优分割，将GrabCut算法的图像分割问题变成最小分割问题[8]。

GrabCut算法的改进思路为：首先对图像进行由RGB到CIELab的空间转换；再采用SLICO算法预处理图片，尽量取得相似度高且拓扑结构较为规则的块状图；再利用GrabCut算法，以超像素图为基础进行GMM参数估计以及迭代处理过程，即图像分割过程，每次迭代都以前一次迭代分割的结果产生的GMM参数为基础，重构网络图模型[9-11]。

本算法的第一步，将RGB格式的图片转换为Lab格式的图片，利用公式(7)～公式(9)实现。

L=0.212 600 7R+0.715 194 7G+0.072 204 6B，

(7)

a=0.325 896 2R-0.499 259 6G+0.173 340 9B+128，

(8)

b=0.121 812 8R+0.378 561 0G-0.500 373 8B+128。

(9)

将产生的Lab图像采用SLICO算法进行处理，得到规则的超像素图(见图5～图7)。

获取超像素图后，再用超像素区域替换人为划定的初始前景区域，最终使用GrabCut算法进一步优化超像素图的前景/背景区域。由GrabCut算法的原理可知，因为原始的像素点被超像素取代，所以这里要添加超像素尺寸(包括像素个数)，从而公式(6)应变成：

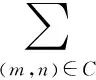
(10)

式中：λ=sm/sn，该式代表m超像素与n超像素的比率。

GrabCut算法在每一次迭代中，都会将除目标以外的所有图像当作背景来处理，这不仅要增加顶点数，而且目标周围相似的背景还会干扰GMM的计算，从而造成偏差[6]。因此，为了降低超像素平均颜色造成的误差，并避免对于SLICO分割精度的过度依赖，在前几次超像素图像上的迭代优化后的GMM的基础上，再对原Lab图像采取像素级的GrabCut分割，从而得到效果比较理想的分割标记结果；再将此标记替换到原始RGB图像上[17]，得到最终的分割图像。

3.2 改进的GrabCut算法图像分割结果

对样本库一中单一目标、样本库二中多目标、样本库三中复杂背景下的木材表面缺陷图像，采用改进GrabCut算法进行试验，图像分割步骤见图8。试验的GMM更新迭代次数设为5，超像素的个数设为600。采用的缺陷图像大小均为512×512的彩色图像。在试验过程中，用户首先输入相同的初始矩形框。

3.2.1 单个目标的分割试验结果

单个活节分割结果(见图9)：虽然活节缺陷与边缘背景的灰度值像素差别很小，并且边缘部分有些模糊；但改进的GrabCut算法可以实现完整的分割轮廓，且基本不存在过分割和欠分割的问题，分割轮廓曲线平滑完整，分割时间为5 453.814ms。

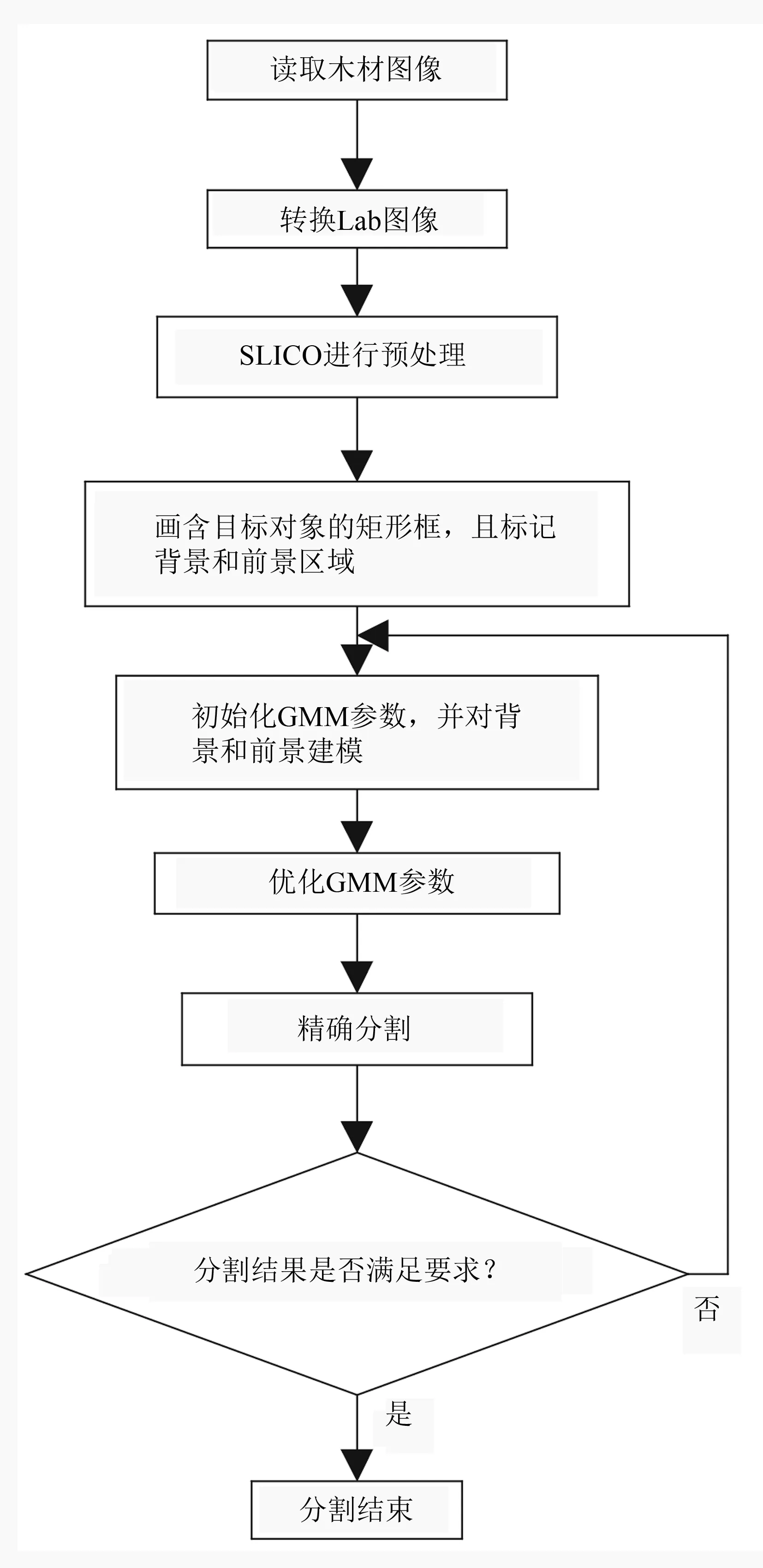
图8 改进GrabCut算法的图像分割步骤

单个虫眼分割结果(见图10)：改进GrabCut算法的分割轮廓曲线完整，分割效果较好，没有过分割和欠分割问题，且分割时间为4 442.29ms。

单个死节分割结果(见图11)：改进GrabCut算法的分割结果效果好，分割轮廓曲线完整，且分割时间为2 485.93ms。

根据试验结果图(见图9～图11)可知，改进GrabCut算法能够不受木材表面缺陷的多少、大小和缺陷轮廓形状的影响，分割效果好，分割轮廓曲线平滑完整，基本不存在过分割和欠分割的问题，且分割速度快、抗噪性强、运行时间短。

3.2.2 多个目标的分割试验结果

多个活节分割结果(见图12)：改进GrabCut算法能够将木材表面的每一个活节缺陷都分割出来，且分割轮廓曲线平滑完整，没有欠分割和过分割问题，且分割时间为8.223s。

图9 单活节缺陷表面图像分割

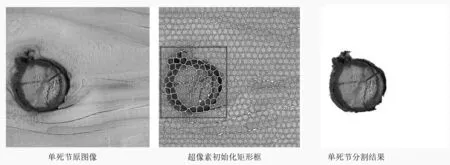
图11 单死节缺陷表面图像分割

图12 多活节缺陷表面图像分割

多个虫眼分割结果(见图13)：改进GrabCut算法能够快速锁定木材表面的每一个虫眼缺陷，且分割轮廓曲线完整，分割效果好，分割时间为7.718s。

图13 多虫眼缺陷表面图像分割

多个死节分割结果(见图14)：改进GrabCut算法能够将木材表面的每一个死节缺陷都分割出来，且分割轮廓曲线平滑完整，分割时间为5.944s。

图14 多死节缺陷表面图像分割

根据试验结果(见图12～图14)可知，改进GrabCut算法能够快速锁定木材表面的多个缺陷，且不受木材表面缺陷的多少、大小和缺陷轮廓形状的影响，分割效果好，分割轮廓曲线平滑，分割效率高，抗噪性好。

3.2.3 整块板材的分割试验结果

为了验证改进GrabCut算法对木材表面缺陷分割的实用性以及检测1m长木材表面上的节子和虫眼个数，对样本库三中的复杂背景的1m长整块板材的图像(3 456×2 304)进行试验(见图15～图17)。观察最终分割结果图可知，改进GrabCut算法能够将缺陷从整块板材中有效地分割出来，不受形状、位置、面积大小等限制，同时也不受木材自身纹理的干扰，分割轮廓线平滑完整，分割效果较好，分割速度快，分割时间分别为27.543、23.233、26.768s。

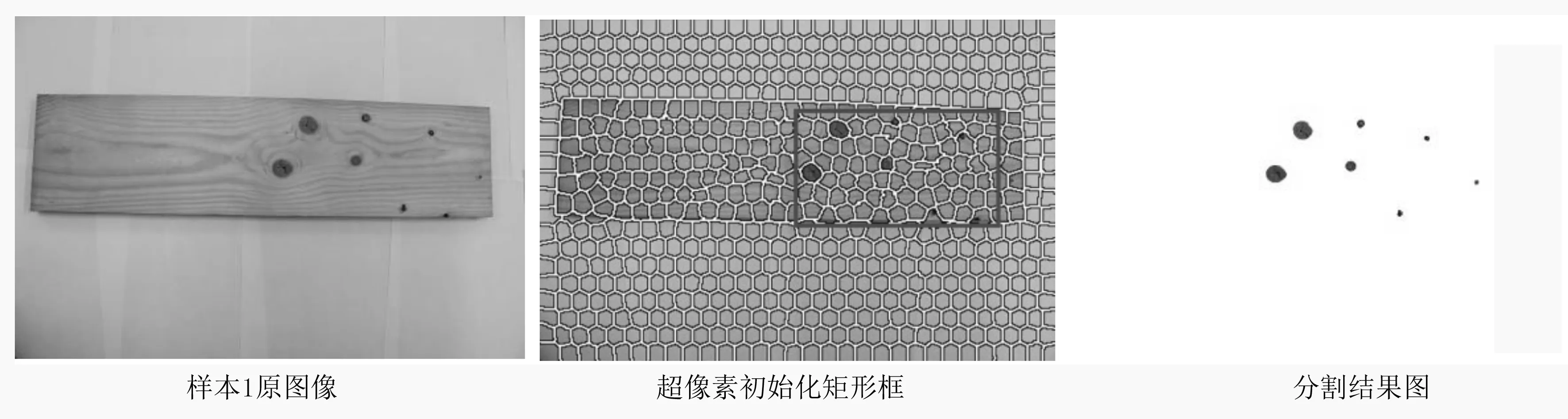
图15 样本1木材表面缺陷分割

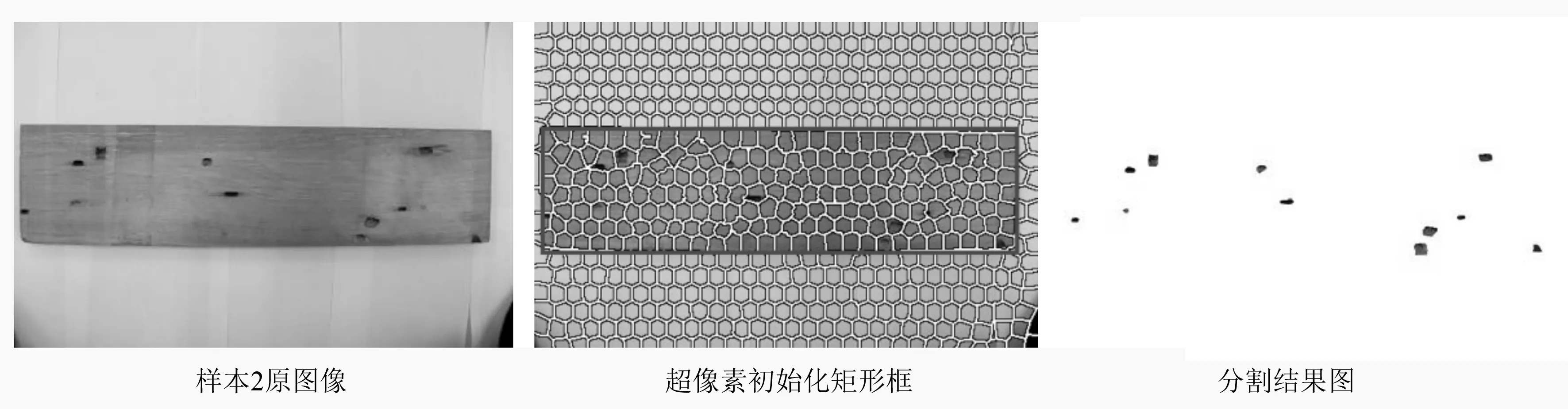
图16 样本2木材表面缺陷分割

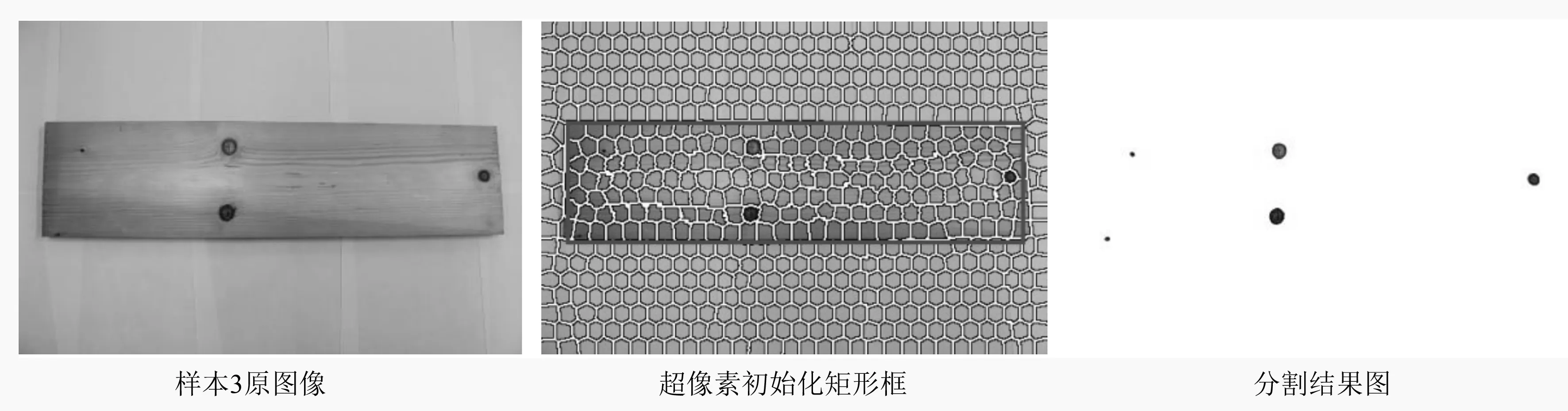
图17 样本3木材表面缺陷分割

4 GrabCut算法与改进的GrabCut算法比较

为了更明显地验证改进GrabCut算法的优越性，对图18～图20的木材表面缺陷图像分别采用GrabCut算法、改进GrabCut算法进行分割试验。

从传统算法的试验结果可知：传统GrabCut算法对活节图像分割时，受背景纹理干扰，存在一定的过分割噪点；对虫眼图像分割时，能够基本实现缺陷轮廓分割，但是受到虫眼缺陷区域边界凹凸的细小纹理干扰，导致缺陷低部出现少量过分割噪点；对死节图像分割时，能够实现完整分割，但分割曲线不够平滑。

图18 单活节图像分割

图19 单虫眼图像分割

图20 单死节图像分割

从改进算法的试验结果可知：改进GrabCut算法能够克服传统GrabCut算法进行处理时出现的过分割问题，抗噪性强，不受背景区域凹凸纹理的干扰，对活节、虫眼、死节3种缺陷分割时，均能快速锁定缺陷，实现完整分割，且分割轮廓曲线平滑完整，基本不存在过分割和欠分割问题。由表1可见，改进GrabCut算法完成缺陷完全分割的运行时间，少于GrabCut算法。

表1 2种算法完成缺陷完全分割的运行时间 ms

5 结论

SLIC和SLICO算法能够得到较为规则的超像素块，且SLIC和SLICO算法运行时间均小于分水岭算法，其中SLICO算法能够得到更加规整的超像素块。

采用改进GrabCut算法分别对单目标、多目标、复杂背景下多目标的木材表面缺陷的图像进行分割试验，从试验结果看出，改进GrabCut算法能够改善传统GrabCut算法会出现的欠分割和过分割问题，抗噪性强，不受背景区域凹凸纹理的干扰，且分割轮廓曲线平滑完整，分割速度快，运行时间短。

通过改进GrabCut算法和传统GrabCut算法的对比试验看出，改进GrabCut算法比传统GrabCut算法在时间上具有很强的优势，分割效率高，且抗噪性好、分割效果好。

[1] 冈萨雷斯.数字图像处理[M].电子工业出版社，2005.

[2] 周宝.基于超像素聚类的图像分割方法研究[D].南京：东南大学，2015.

[3] 胡志立.基于改进GrabCut的彩色图像快速分割方法研究[D].西安：陕西师范大学，2014.

[4] 刘毅.基于图割的交互式图像分割算法研究[D].南京：南京理工大学，2013.

[5]SEFIDPOURA，BOUGUILAN.Spatialcolorimagesegmentationbasedonfinitenon-Gaussianmixturemodels[J].ExpertSystemswithApplications，2012，39(10)：8993-9001.

[6] 胡志立，郭敏.基于SLIC的改进GrabCut彩色图像快速分割[J].计算机工程与应用，2016，52(2)：186-169.

[7] 郭振峰.基于GraphCuts的交互式图像分割[D].长沙：中南大学，2013.

[8] 白雪冰，王林.基于空频变换的木材缺陷图像分割[J].东北林业大学学报，2010，38(8)：71-74.

[9] 周良芬，何建农.基于GrabCut改进的图像分割算法[J].计算机应用，2013，33(1)：49-52.

[10] 陈鑫，何中市，李英豪.一种新的基于SLICO改进的GrabCut彩色图像分割算法[J].计算机应用研究，2015，32(10)：3191-3195.

[11]VCHAP，HAINDM，SUKT.ColourandrotationinvarianttexturalfeaturesbasedonMarkovrandomfields[J].PatternRecognitionLetters，2011，32(6)：771-779.

ImageSegmentationofWoodSurfaceDefectsbyImprovedGrabCutAlgorithm

//Bai Xuebing, Song Enlai, Li Runjia, Xu Jingtao

(Northeast Forestry University, Harbin 150040, P. R. China)

The traditional GrabCut algorithm and the improved GrabCut algorithm are used to simulate the multi-target wood surface defect images in single target, multi-target and complex background. The improved GrabCut algorithm was optimized for the defect image segmentation of the wood surface, which could effectively improve the defects of the traditional GrabCut algorithm, such as under-segmentation, over-segmentation, and susceptible to interference from regional bumps. The segmentation of all kinds of wood surface defects images achieves better results, and the improved GrabCut algorithm is with its advantages and feasibility.

Wood surface defects; Wood image segmentation; GrabCut algorithm

TP317.4

1)黑龙江省自然科学基金项目(C201208)。

白雪冰，男，1966年5月生，东北林业大学机电工程学院，教授。E-mail：xumou2010@163.com。

宋恩来，东北林业大学机电工程学院，硕士研究生。E-mail：247367803@qq.com。

2017年5月16日。

责任编辑：张 玉。

//Journal of Northeast Forestry University，2017,45(10)：64-71.