“甲虫爬环”问题求解的3个关键环节
于志明
(连云港师范高等专科学校物理系,江苏 连云港 222006)
“甲虫爬环”问题求解的3个关键环节
于志明
(连云港师范高等专科学校物理系,江苏 连云港 222006)
“甲虫爬环”问题:[1]质量为m1的甲虫,在质量为m2、半径为r的圆环上爬行,圆环放在光滑的水平桌面上,开始时甲虫和圆环都是静止的.要求: (1) 甲虫在圆环上爬行一周时,圆环自身转过的角度.(2) 若甲虫以相对速度u沿逆时针方向在圆环上爬行,甲虫和环心相对于桌面运动的速度.(3) 运动开始时甲虫与圆环接触点的运动轨迹.
这道题的求解对于中学生来讲有一定难度,下边谈谈求解这道题的3个关键环节.
1 质心知识的应用
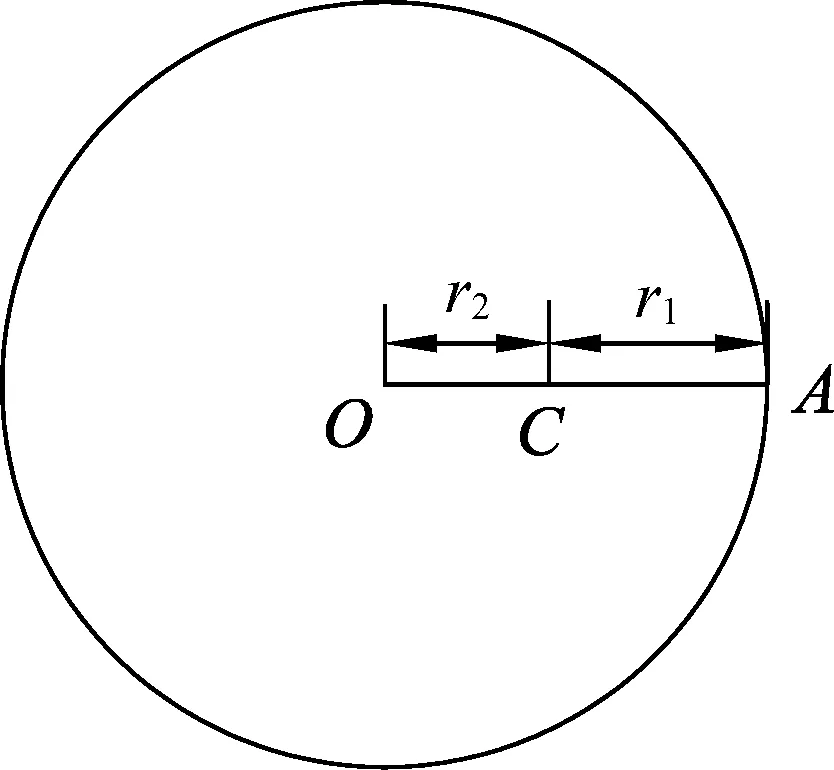
图1
将甲虫和圆环组成一个质点系,设开始时甲虫位于圆环上的A点,甲虫和圆环组成的质点系的质心为C,甲虫到C的距离为r1,圆环的圆心O到C的距离为r2,如图1所示.则
m1r1=m2r2.
(1)
r1+r2=r.
(2)
所以
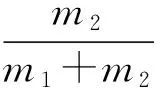
(3)
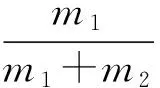
(4)
由于开始时甲虫和圆环在水平桌面上都是静止的,水平桌面是光滑的,根据质心运动定理可知,由甲虫和圆环组成的质点系的质心C在水平桌面上是始终静止不动的.而当甲虫在圆环上爬行时,由于r1、r2大小恒定,故甲虫和环心都在桌面上做以C为圆心的圆周运动,且具有相同的角速度.
根据质心的知识确定甲虫和圆环组成的质点系的质心的位置、质心在桌面上静止、甲虫爬行时甲虫和环心都在桌面上做以质心为圆心的圆周运动,这是求解这道题的第1个关键环节.
2 爬行条件的应用
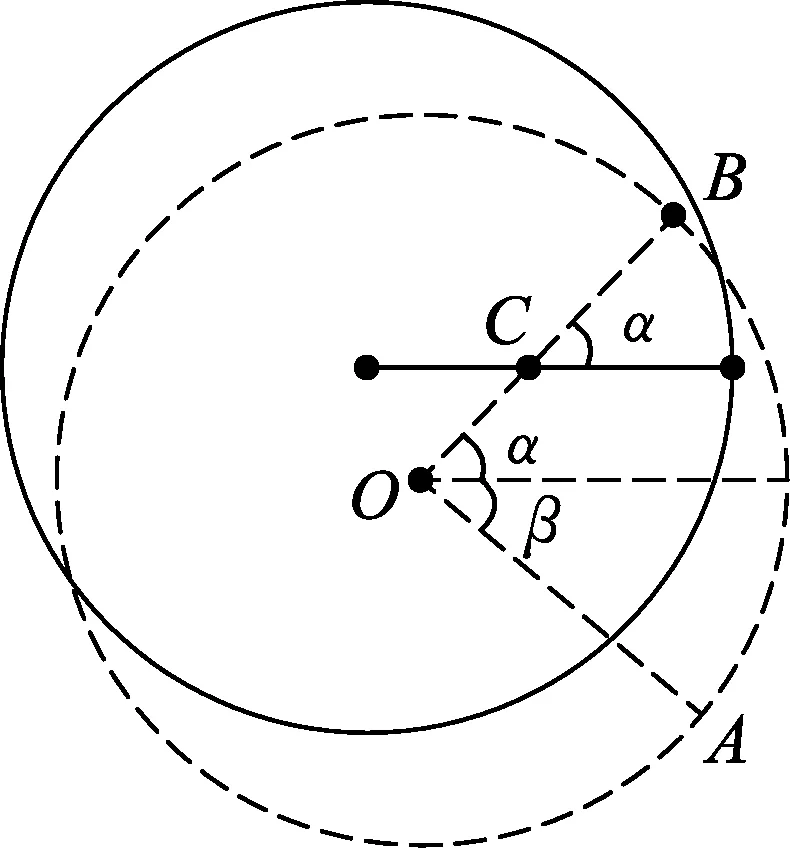
图2
设甲虫在圆环上以匀相对速度u沿逆时针方向爬行,由于桌面是光滑的,当甲虫在圆环上爬行时,圆环将沿顺时针方向向下转动,同时圆环的环心O将向下移动,而环心O到C的距离保持不变.设甲虫开始爬行时圆环的位置如图2中的实线所示,而甲虫爬行t时间后,圆环的位置如图2中的虚线所示,此时甲虫位于圆环上的B点,甲虫相对于桌面沿逆时针方向绕质心C转过的角度为α,而开始时甲虫在圆环上的接触点A绕环心O沿顺时针方向转过的角度为β,在t时间内甲虫在圆环上由A点爬行到了B点,爬过的弧长为ut.由图2可知,
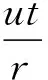
(5)
上式两边对时间t求导得
(6)
3 角动量守恒定律的应用
在本题中,由甲虫和圆环组成的质点系对其质心C的角动量是守恒的.甲虫对于质心C的角动量为
(7)

(8)
由于甲虫和圆环组成的系统开始时是静止的,故由角动量守恒定律得
(9)
将式(9)和式(6)联立求解得
(10)
(11)
将式(3)、(4)代入式(10)、(11)可得
(12)
(13)
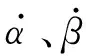
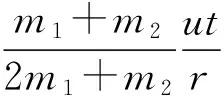
(14)

(15)
有了α和β随时间t的变化关系,“甲虫爬环”的所有问题就可以迎刃而解了.
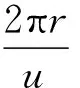
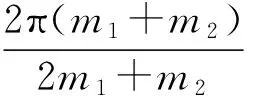
(16)
而由式(15)可知此时圆环上的A点在桌面上绕环心O转过的角度为
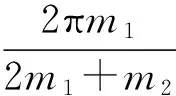
(17)
且
α+β=2π.
(18)
(2) 由式(14)和式(3)、(4)可得甲虫和环心O在桌面上绕质心C圆周运动的速度分别为
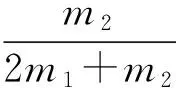
(19)
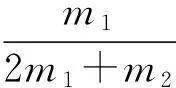
(20)
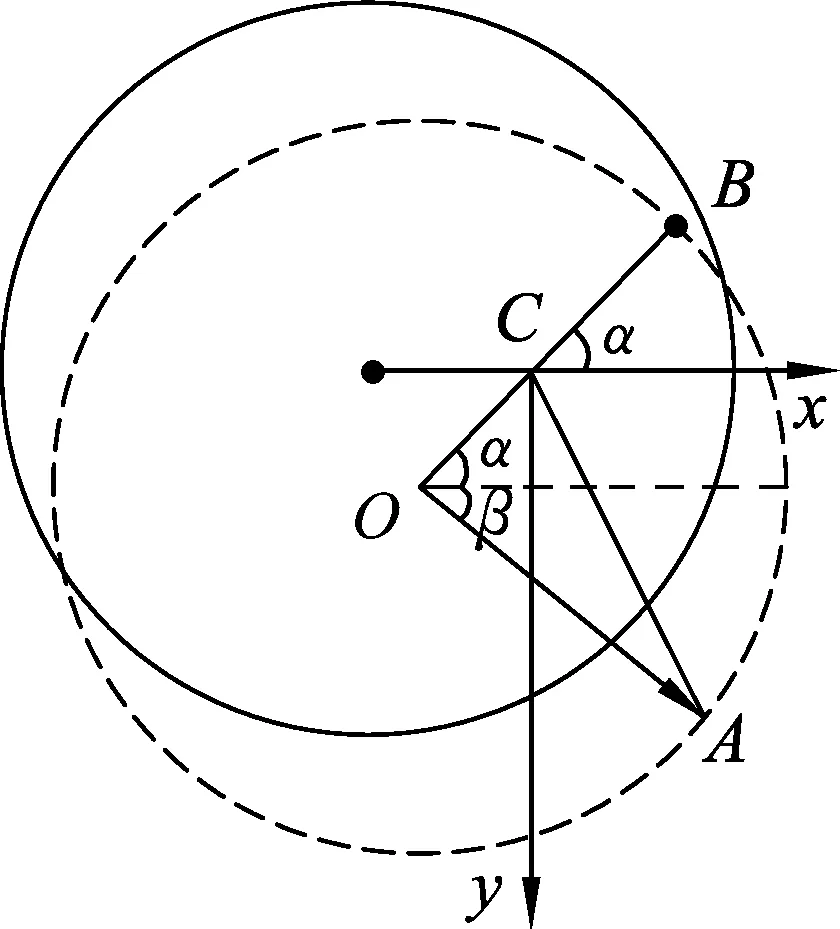
图3
(3) 建立以质心C为原点的静止在桌面上的直角坐标系C-xy,如图3所示.由图3可知,圆环上的A点在C-xy中的坐标为
x=rcosβ-r2cosα.
(21)
y=rsinβ+r2sinα.
(22)
将式(3)、(4)、(14)、(15)代入式(21)、(22)即得A点的坐标随时间t的变化关系为
(23)
(24)
式(23)、(24)就是圆环上的A点在桌面上运动的轨迹方程.可以肯定的是如果m2≫m1,则质心C就非常靠近环心O,A点运动的轨迹就非常接近于圆环.
1 李力,张银.“甲虫爬环”问题的解析[J].大学物理,2016,35(8):22-24.
2 哈尔滨工业大学理论力学教研室编.理论力学[M].北京:高等教育出版社,2012.
2017-03-02)

