分离压和表面黏度的协同作用对液膜排液过程的影响∗
叶学民 杨少东 李春曦
(华北电力大学,电站设备状态监测与控制教育部重点实验室,保定 071003)
分离压和表面黏度的协同作用对液膜排液过程的影响∗
叶学民 杨少东 李春曦†
(华北电力大学,电站设备状态监测与控制教育部重点实验室,保定 071003)
针对含不溶性活性剂的垂直液膜排液过程,在考虑分离压作用的前提下,引入随活性剂浓度变化的表面黏度模型,应用润滑理论建立了液膜厚度、活性剂浓度和液膜表面速度的演化方程组,通过数值计算分析了常表面黏度和变表面黏度情形下的液膜演化特征.结果表明:表面黏度是影响液膜排液过程的重要因素,当不考虑表面黏度时,液膜表面呈“流动”模式,反之呈“刚性”模式,且随表面黏度增加,液膜排液速率明显减缓.分离压对“黑膜”的形成至关重要,分离压单独作用时,其形成的“黑膜”长度较短,而只考虑表面黏度时,则不能形成稳定的“黑膜”.而在二者协同作用下,液膜中部形成了向下扩展、厚度很薄但非常稳定的“黑膜”,且“黑膜”厚度、出现时间均随表面黏度的增大而增加.当考虑活性剂浓度对表面黏度的影响时,表面速度受此影响显著;在形成“黑膜”长度及出现时间方面与相应常表面黏度的情形基本类似,但其“黑膜”厚度小于相应常表面黏度,故在液膜排液过程中更容易发生失稳.
排液,分离压,表面黏度,黑膜
1 引 言
液态泡沫独特的流变特性及稳定性一直是软物质领域研究的热点.垂直液膜排液过程是泡沫渗流[1]过程的简化模型,研究其影响因素有利于揭示泡沫渗流机理,为泡沫在工程中的高效应用,如洗涤剂、食品、石油开采、泡沫钻井、泡沫驱油、泡沫灭火等提供理论基础[2−5].
液膜排液过程的研究始于Mysels等[6]的开创性实验,其发现液膜排液过程的快慢与溶液中活性剂浓度密切相关,并在排液过程的后期,液膜表面会驻留一厚约几十纳米且透明的“黑膜”.此后,众多研究表明,影响液膜排液过程的重要因素包括分离压和溶液表面的黏弹性质[7−9].在分离压影响方面,Schwartz和Roy[10],Carey和Stubenrauch[11],Tabakova和Danov[12]开展了重要的工作,均认为分离压在薄膜排液过程的作用不容忽视.而溶液的表面黏弹性包含表面黏性和表面弹性.表面黏性是指液体表面单分子层的黏性,用表面黏度来度量.其作用主要体现在影响气液界面上的切应力平衡[13].Boussinesq[14]提出表面黏度包括表面剪切黏度和表面膨胀黏度(也称扩展黏度[15]).已有学者通过理论模拟和实验研究探讨了表面黏度对液膜界面性质的影响.Matar[13]利用线性稳定性和自相似性理论对液膜稳定性进行了研究,发现增大表面黏度可延缓液膜破裂.Braun等研究了常表面黏度[16,17]及表面黏度随活性剂浓度变化时[18,19]的排液过程,指出表面黏度对展向扰动具有稳定作用,液膜局部增厚或变薄是重力、Marangoni力及黏性力相互竞争的结果;虽然模拟结果与Snow等[20]的实验结果符合得很好,但仍对液膜底部的复杂结构这一实验现象未能解释,需要进一步完善描述界面性质的理论模型.Lopez和Hirsa[21]模拟了表面黏度对两同心圆筒间液膜流动的影响,并引入表面黏度受活性剂浓度影响的非线性方程,发现径向应力平衡由Marangoni应力主导,而切向应力仅与表面剪切黏度有关.Vitasari等[22]考虑了表面黏度对液膜演化和表面活性剂分布的影响,指出表面黏度较低时,液膜演化速度较快,活性剂浓度在整个演化过程均较低;而表面黏度较高时,演化速度较慢,液膜主要部分的活性剂浓度保持均匀分布.
液膜中添加表面活性剂将引发表面张力的不均匀性,由此诱发的Marangoni效应是影响液膜界面性质的重要因素,Elfring等[23]指出Marangoni效应与界面表面黏度密切相关.Yekeen等[24]通过实验发现,将纳米颗粒加入到含表面活性剂的泡沫液膜中,表面黏度由20.34 mPa·s增至84.84 mPa·s,同时液膜厚度从27.5µm增至136µm.由此可见,纳米颗粒的加入导致液膜表面黏度的增加与液膜厚度密切相关.韩国彬等[25]利用表面波技术研究了消泡剂TBP对C12E8表面流变性质的影响,实验表明,TBP能大幅度降低C12E8的表面膨胀黏度,从而削弱C12E8表面膜的强度和泡沫稳定性.
目前认为,垂直流动的液膜表面存在“刚性(rigid)”和“流动(mobile)”两种模式.Gauchet等[26]通过实验研究了含SDS液膜的表面流动模式,发现较大的表面黏度可促使液膜表面刚性化.Naire等[16]基于对一端固定的垂直液膜排液过程的数值研究,指出增大表面黏度可观察到液膜表面由流动态向刚性态的转变.
表面黏弹性质中的另一个重要方面是表面弹性,这也是影响液膜排液过程的重要因素.Saulnier等[27]和Sett等[28]通过实验发现表面弹性高的液膜存续时间较长,而表面弹性低的液膜存续时间较短.Zang等[29]研究了二氧化硅纳米颗粒在气液界面的性质,发现颗粒的气液接触角在90°时,其液膜表面弹性达到最大值,并认为表面弹性最大时泡沫起泡性和稳定性也同时达到最大.Pu等[30]在研究三种聚合物(HAWP,CP,XG)液膜的稳定性中发现,在不同聚合物液膜中,表面黏性和表面弹性起到的主导作用不同.在HAWP液膜中,表面黏性在液膜稳定性方面起主要作用;而在XG液膜中,表面弹性作用则更大.张春荣[31]采用界面张力弛豫实验研究了非离子表面活性剂NP-8,NP-10和NP-12的表面黏弹性质,发现表面弹性大的体系其泡沫稳定性高;另外,其在SDBS和TX-100溶液中分别加入MO-4000(高分子聚合物)和聚丙烯酰胺(HMPAM)后发现泡沫稳定性得到极大提高,认为聚合物的加入导致液膜表面黏度增加,从而抑制表面膜的变薄.Tian等[32]认为表面弹性与表面黏性的作用很难区分,加之本文更多关注表面黏性,因而在建模中暂时不考虑表面弹性.
综上所述,表面黏度和分离压是影响垂直液膜排液稳定性的重要因素,且表面黏度和分离压均与活性剂浓度密切相关[33−36].然而已有研究均单纯考虑分离压或表面黏度的单一作用,尚未见考虑二者协同作用下垂直液膜排液过程的研究报道.为此,本文在考虑分离压的前提下,将随活性剂浓度变化的表面黏度模型引入垂直液膜排液过程,探讨表面黏度对排液过程的影响,进而为泡沫液膜的稳定性研究及其调控提供理论基础.
2 理论模型
如图1所示,垂直流动的二维液膜其顶端和底端分别固定在金属框上,表面活性剂分布在气液界面.为使问题简化,假设排液液体为黏性不可压缩流体,且忽略液膜表面蒸发对排液过程的影响.液膜厚度z=±h(x,t),且关于中心线z=0对称,因此只需考虑z≥0侧的液膜变化即可.液膜初始厚度h0与流动方向尺度L相比非常小,即δ=h0/L≪1,适用于润滑理论[37,38].

图1 垂直液膜排液过程示意图Fig.1.Schematic diagram of a vertical fi lm drainage.
2.1 控制方程
控制方程包括连续性方程和运动方程:
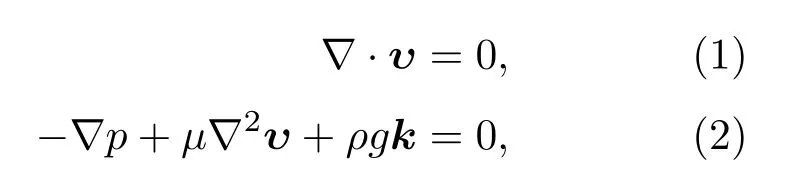
式中:υ=(u,υ),k=(1,0);µ,ρ分别为流体的动力黏度、密度;p为流体的压强;g为重力加速度;∇和∇2分别为哈密顿算子和拉普拉斯算子.
边界条件为

下角标表示对该变量求偏导,下同.
自由液面上的运动学条件为
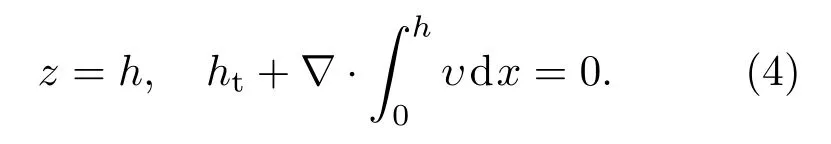
切向应力τ和表面压力ps在液膜表面满足力平衡条件:

(5)式和(6)式中,n和t分别为液膜表面处的单位法线矢量和单位切线矢量;T为液体的应力张量,其一般形式为T=−pI+µ(∇υ+∇υT),其中I为单位张量;下角标“s”代表液膜表面,下同.
将x方向上的排液速度u分解为滑移速度u0和剪切速度u1[10,39],即

且满足在z=h处,u1=0.因此u0也可视为液膜表面速度.
活性剂浓度的对流扩散方程为

式中,Γ代表活性剂浓度;D为扩散系数;J为液膜表面与内部活性剂单体间的吸附通量,对于不溶性活性剂,J=0.
在液膜表面,切应力τ有如下关系:

(9)式中,µs是表面剪切黏度,σ为表面张力;(6)式中,液膜表面压力由毛细力和分离压组成,

(10)式中,κ为液膜表面曲率,κ=hxx/(1+h2x)3/2;Π代表分离压.
当液膜中含表面活性剂时,表面张力与活性剂浓度间的关系为

其中β为与浓度有关的系数,σ0表示不含表面活性剂时液膜的表面张力,Γ0是初始活性剂浓度.
为凸显表面黏度的影响,下文采用不随活性剂浓度变化的分离压模型[10]:

(12)式中,h∗为液膜平衡厚度.
2.2 无量纲化
采用如下无量纲变换式(上标“∗”表示无量纲量):

(13)式中,G∗,D∗,S∗分别代表无量纲活性剂浓度、表面活性剂扩散系数以及表面黏度,且

将(13)和(14)式代入(1)–(7)式,利用润滑理论,并结合质量守恒积分表达式,

其中Q∗为体积流量.则无量纲液膜厚度和切应力可表示为:

2.3 无量纲方程组
将(9)–(12)式代入(16)–(17)式,并将(8)式进行无量纲化,经推导最终可得液膜厚度h,活性剂浓度G和表面速度u0的非线性偏微分方程组(为描述方便,以下省略上标“∗”):

表面黏度S与当地活性剂浓度密切相关,故采用随活性剂浓度变化的表面黏度模型[18],

(21)式中,Sm是无量纲表面剪切黏度,F(ζG)是关于活性剂浓度的非线性关系,ζ是无量纲参数,这里参考前人结果[18,19,21],使用如下非线性表达式:

图2 表面黏度与活性剂浓度间的关系Fig.2.Relation of surface viscosity and surfactant concentration.

式中,ζ取0.001.图2给出了表面黏度与活性剂浓度的关系.
2.4 边界条件
液膜两端厚度恒定,以模拟液膜随同金属框被完全提拉出溶液后的情形:

两端无流体流动也无活性剂流动:

2.5 初始条件
无量纲厚度初始条件:
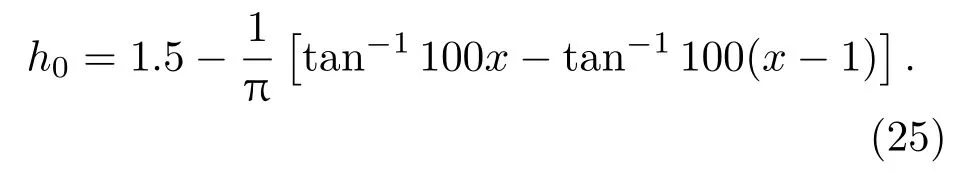
无量纲浓度初始条件:初始活性剂浓度分布均匀,文中取值如下:

3 数值模拟
采用FreeFem程序求解演化方程组(18)–(20).根据流动尺度选取0<x<1的一维区域进行计算,在满足精度和减少计算时间的条件下,将计算区域划分为100个均匀网格.本文参照文献[10]的数据,并结合文献[27,28,40],得到文中物性参数及无量纲参数的取值范围如表1所列,下文模拟中无量纲参数的选取即以此为基础.

表1 典型尺度及无量纲参数数值范围Table 1.Typical scale and dimensionless parameters in experiments.
4 模拟结果与分析
表面黏度和分离压是影响垂直液膜排液过程中液膜稳定性的重要因素,为研究二者协同作用下的垂直液膜排液特征,首先对分离压和表面黏度的单一作用进行分析,然后考虑二者的协同作用.
4.1 分离压和表面黏度单一作用下的排液过程
图3给出了只考虑分离压情形下的液膜流动特征.该图表明,演化前期(t=0–7×10−6),流体在重力作用下迅速向下排液,因而在演化初期,液膜表面速度较大且液膜迅速变薄;当演化到一定程度时,液膜中的分离压将发挥作用,阻滞液膜的排液变薄[10];随活性剂不断在液膜底端积累,使该处表面张力逐渐减小,从而诱发产生Marangoni效应,当其强度与重力排液作用达到平衡时,液膜底端表面速度降为0,其底部(0.7<x<1)发生刚性化,而中上部(0<x<0.7)由于Marangoni效应不能克服重力排液机理,故该处的液膜表面仍呈“流动”模式.Heidari等[19]在对一端固定的垂直液膜进行排液研究时,同样发现液膜表面“部分”刚性化的现象(本文在不引起歧义的情况下,将表面“部分”刚性模式划分为“流动”模式),虽然其考虑了表面黏度的影响,但由于所设定的表面黏度值很小,对排液影响几乎可以忽略.故可得出:当不考虑表面黏度作用时,液膜表面呈“流动”模式,此时t=3×10−2,如图3(a)所示,液膜在x≈0.07位置处会出现液膜厚度的最小值,这与实验中的“黑膜”区域相对应.为此,下文以“黑膜”区泛指最小液膜厚度附近的区域(由于本文所建分离压模型并没有考虑短程结构斥力,因而“黑膜”应为普通黑膜).
当表面黏度单独作用时,其液膜流动特征如图4所示.演化初始,液膜流体在重力作用下迅速变薄,但由于没有考虑分离压作用,无法阻碍液膜排液的持续变薄过程,虽然在t=1×10−5时出现了所谓的“黑膜”,但其不能稳定存在.随后,在t=1.55×10−5时液膜变薄、破断,发生“老化(ostwald ripening)”.继续提高表面黏度,除了可以延缓液膜“老化”时间外,均不能形成稳定存在的“黑膜”.在实际液膜排液过程中,液膜中部会形成非常稳定的“黑膜”,且其“寿命”很长[6].由此说明分离压对液膜排液稳定性及“黑膜”存续方面起到重要作用.

图3 不考虑表面黏度时的排液特征 (a)液膜厚度;(b)活性剂浓度;(c)早期表面速度;(d)后期表面速度Fig.3.Characteristics of fi lm drainage without surface viscosity:(a)Film thickness;(b)surfactant concentration;(c)surface speed in early time;(d)surface speed in late time.

图4 不考虑分离压时的排液特征 (a)液膜厚度;(b)活性剂浓度;(c)早期表面速度;(d)后期表面速度Fig.4.Characteristics of fi lm drainage without disjoining pressure:(a)Film thickness;(b)surfactant concentration;(c)surface speed in early time;(d)surface speed in late time.
4.2 分离压和表面黏度协同作用下的排液过程
4.2.1 常表面黏度时的排液过程
图5为在考虑分离压前提下,表面黏度S=200时的排液特征.首先,垂直液膜受重力作用,顶端液膜不断变薄,因液膜在金属框底端固定,则会在底端附近形成一个不断变厚的球形凸起.顶端的表面活性剂在流体“冲刷”下,不断向液膜底端“富集”.此时,由图5(c)可知,演化早期的表面速度虽然在不断减小,但未出现“逆流”现象.随表面活性剂在底部的不断积累,逐渐形成自下向上的活性剂浓度梯度,由此产生Marangoni效应;当Marangoni效应足够大时,引发液膜表面上的流体携带活性剂一起向上移动,发生“逆流”现象(图5(d)),此时下部的活性剂不断地被携带到液膜上部,使活性剂浓度重新分布(图5(b));随演化持续,液膜表面速度不断减小趋于0,此时,液膜表面呈“刚性”模式.结合图6可知,在液膜表面发生“刚性化”后,液膜厚度几乎不再发生变化.最终,液膜中间部分会形成一厚度极薄的区域,且其范围从x≈0.1延伸至x≈0.7处.与单独考虑分离压或表面黏度相比,“黑膜”区域明显更薄,且其范围更大.Mysels等[6]在相对较高和相对较低的活性剂浓度下,均观察到了“黑膜”区域的存在,且其长度随时间不断延伸.另外,是否考虑表面黏度将决定液膜表面的流动模式.不考虑表面黏度时,液膜表面呈“流动”模式;反之,液膜表面呈“刚性”模式.这与Gauchet等[26]得出的表面黏度是导致液膜表面刚性化的结论一致.
为进一步探讨表面黏度的作用,图7给出了S=10,200,1000及10000时典型时刻下的表面流动速度.由图7可知,在同一时刻下,表面速度随表面黏度增加而减小.这是因为随表面黏度的提高,增加了表面膜的强度,并提高了Marangoni效应[23](图8为Naire等[16]通过实验数据并转化为无量纲的Marangoni效应与表面黏度的关系),因而减缓了液膜流动速度.这与Naire等[16]得出的表面速度随表面黏度提高而减小的结论完全一致.因整体演化速度的减小,液膜排液变薄过程减慢,故x=0.1处的液膜厚度随表面黏度提高而增厚(图9(a));因金属框两端固定,流体不断积累到液膜底部,受质量守恒约束,表面黏度较大的液膜其厚度反而在液膜底部较薄(图9(b)).
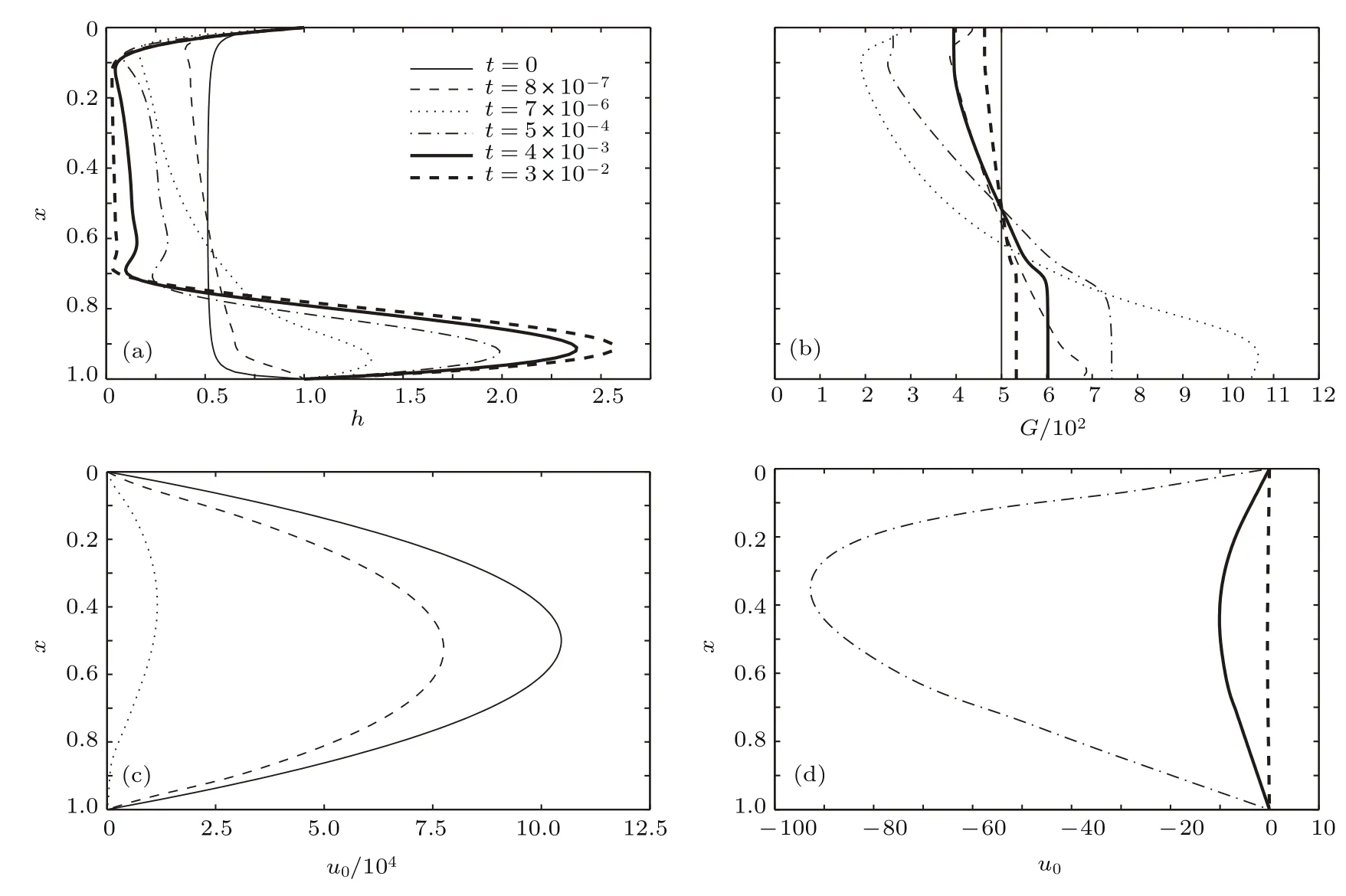
图5 S=200时的排液特征 (a)液膜厚度;(b)活性剂浓度;(c)早期表面速度;(d)后期表面速度Fig.5.Characteristics of fi lm drainage at S=200:(a)Film thickness;(b)surfactant concentration;(c)surface speed in early time;(d)surface speed in late time.

图6 典型位置处液膜厚度的演化过程Fig.6.Evolution of fi lm thickness at typical position.
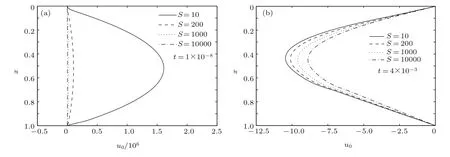
图7 S=10,200,1000,10000时垂直液膜在演化早期和后期的流动速度Fig.7.The fi lm velocity at the early and late stages of evolution at S=10,200,1000,1000.

图8 Marangoni效应与表面黏度的关系[16]Fig.8.The relationship between Marangoni e ff ect and surface viscosity[16].

图9 S=10,200,1000,10000时液膜顶部和底部位置处的厚度Fig.9.Thickness evolution at the top and bottom positions at S=10,200,1000,10000.

图10 S=10,200,1000,10000时“黑膜”区域的厚度Fig.10.Thickness of“black fi lm” at S=10,200,1000,10000.
研究表明[41],“黑膜”处的厚度对于液膜排液稳定性至关重要.这是因为“黑膜”是分离压中范德华引力和静电斥力相互作用达到平衡的结果[11].此时,液膜表面势能最低.当“黑膜”厚度越大,意味着液膜越远离临界液膜厚度,因而其稳定性更好.图10给出了不同表面黏度下的“黑膜”区域厚度,为使其区别更加明显,图10采用了单对数坐标.由图10可知,表面黏度越大,其“黑膜”越厚,相应的液膜稳定性也就越强.
4.2.2 变表面黏度下的排液过程
当表面黏度随活性剂浓度发生变化时,此时整个气液界面的表面黏度不再是定值.图11为Sm=200时的流动特征,其总体演化特征与S=200类似.但不同的是因表面黏度随活性剂浓度发生非线性变化(图12(a)),排液伊始液膜整体表面黏度较小,其表面速度较相应常表面黏度较大(图13(a));随活性剂不断被携带到液膜底部,底端浓度不断增大(图12(b)),进而提高了底部表面黏度及表面膜机械强度[31],使液膜抗扰动能力增加,因而在t=8×10−5时常表面黏度情形下的表面速度反而更慢(图13(b)).当“逆流”现象发生后,活性剂浓度的峰谷差不断减小,因而表面黏度梯度差也在减小,如图12(a)所示.最终,液膜表面速度不断减小趋于0,液膜表面呈现“刚性化”.同时,液膜中部出现“黑膜”,其形状与常表面黏度(图5)的情形类似.
常表面黏度与相应变表面黏度间的“黑膜”区域厚度比较见图14.由图14可知,当考虑活性剂浓度对表面黏度的影响时,其“黑膜”区厚度小于相应常表面黏度的情形,故可得出变表面黏度情形下的液膜排液过程较常表面黏度更容易发生失稳.

图11 表面黏度随活性剂浓度变化时的排液特征 (a)液膜厚度;(b)活性剂浓度;(c)早期表面速度;(d)后期表面速度Fig.11.Characteristics of fi lm drainage when the surface viscosity depends on the surfactant concentration:(a)Film thickness;(b)surfactant concentration;(c)surface speed in early time;(d)surface speed in late time.

图12 典型位置处表面黏度和活性剂浓度的演化历程Fig.12.The evolution of surface viscosity and surfactant concentration at typical locations.

图13 常表面黏度与变表面黏度在典型时刻下的速度比较Fig.13.Comparison of constant and variable viscosity of velocity at typical moment.

图14 常表面黏度与变表面黏度的“黑膜”厚度比较Fig.14.Comparison of“black fi lm”thickness between constant and variable surface viscosity.
4.3 讨 论
4.1 和4.2节讨论了表面黏度和分离压单独作用及协同作用下的排液特征.分离压对于液膜排液稳定性及“黑膜”形成方面起重要作用,当不考虑分离压时,液膜将快速发生“老化”,无法形成稳定的“黑膜”.然而,在实际观察中,液膜中部会驻留稳定性很好的“黑膜”,且持续存在的时间很长,如同“石化”一样[42].因而本文在探讨表面黏度作用时以考虑分离压为前提是合理的.
随后在分离压和表面黏度协同作用下,讨论了常表面黏度及变表面黏度情形下的液膜流动特征.结果表明,不考虑表面黏度下的液膜表面呈“流动”模式,且其“黑膜”长度较短,而考虑表面黏度时的液膜表面呈“刚性”模式,且随表面黏度增大,液膜表面速度逐渐降低.这与Braun等[43]的模拟结果完全一致.此时,液膜中部会形成较长的“黑膜”区域,Mysels等[6]和Saulnier等[27]在对含活性剂液膜的排液实验中均观察到了这一现象的存在.此外,Karakashev和Nguyen[44]对含SDS活性剂液膜排液过程的实验研究发现,在表面黏度为0.03 s.p.情形下的“黑膜”厚度约为16 nm,增加表面黏度至0.18 s.p.,“黑膜”厚度增至约20 nm.本文亦得出“黑膜”厚度随表面黏度的增加而增厚的结论.在“黑膜”形成时间方面,由Karakashev和Nguyen[44]的实验数据知,表面黏度越大,其出现时间越晚.在本文中,各种情形下“黑膜”出现时间如图15所示,其特征与文献[44]的实验结果基本一致.这是因为随着表面黏度的增大,减缓了液膜排液变薄过程,故延缓了“黑膜”出现时间.同时,由图15知,当考虑活性剂浓度对表面黏度影响时,其对“黑膜”出现时间方面的影响不是很大.

图15 不同表面黏度下的“黑膜”出现时间Fig.15.The time of appearance of“black fi lm”under the di ff erent surface viscosity.
另外,在Braun等[18]的变表面黏度数值模拟过程中发现,液膜顶部活性剂几乎为0,而本文数值模拟中并未得出这一结果,这是因为本文模型中考虑了分离压的作用,由于分离压减缓了液膜顶部的排液变薄,进而减缓了该位置活性剂浓度的下降.而现有报道已证明考虑分离压作用的必要性,因此本文所得结果更与实际结果相符.
需要说明的是,表面黏度不仅包含了剪切黏度,还有膨胀黏度.受膨胀黏度测量技术的限制,很多学者为计算方便忽略了膨胀黏度[26,45],本文亦只考虑了剪切黏度的影响.已有实验表明,当溶液中含有高分子活性剂或活性剂浓度足够大时,膨胀黏度的影响就不能忽略.
5 结 论
1)表面黏度是影响液膜排液过程的重要因素.当不考虑表面黏度时,液膜表面呈“流动”模式;反之,呈“刚性”模式,且随表面黏度增加,液膜的排液速率明显减小,故减缓了液膜的排液变薄过程.
2)分离压对于“黑膜”区域的形成至关重要,分离压单独作用时,其形成的“黑膜”长度较短,而只考虑表面黏度时,则不能形成稳定的“黑膜”.而在二者协同作用下,液膜中部形成了向下扩展、厚度很薄但非常稳定的“黑膜”.另外“黑膜”厚度、出现时间均随表面黏度的增大而增加.
3)当考虑气液界面处的表面黏度随活性剂浓度变化时,表面速度受此影响显著,在演化初期,因表面黏度整体较小,液膜表面速度较大;随液膜底部活性剂浓度不断增加,进而提高了底部表面黏度及表面膜机械强度,使其液膜抗扰动能力增强,延缓了液膜的排液变薄过程,但其流动稳定性小于相应常表面黏度的情形.此外,其对“黑膜”长度及出现时间方面影响不是很大.
4)表面黏度不仅包含剪切黏度,还有膨胀黏度,当活性剂浓度足够大或者气液界面含有高分子时,膨胀黏度的影响就不能忽略,今后的计算模型中应进一步考虑膨胀黏度的影响.
[1]Huang J,Sun Q C 2007Acta Phys.Sin.56 6124(in Chinese)[黄晋,孙其诚 2007物理学报56 6124]
[2]Bournival G,Du Z,Ata S,Jameson G J 2014Chem.Eng.Sci.116 536
[3]Firouzi M,Nguyen A V 2014Adv.Powder Technol.25 1212
[4]Jun S,Pelot D D,Yarin A L 2012Langmuir28 5323
[5]Anazadehsayed A,Naser J 2017Chem.Eng.Sci.166 11
[6]Mysels K J,Shinoda K,Frankel S 1959Soap Films:Studies of Their Thinning and a Bibilography(New York:Pergammon)p116
[7]Wang J,Nguyen A V,Farrokhpay S 2016Adv.Colloid Interfac.228 55
[8]Benjamin Dollet,Isabelle Cantat 2014J.Fluid Mech.739 124
[9]Zang D Y,Rio E,Langevin D,Wei B,Binks B P 2010Eur.Phys.J.E31 125
[10]Schwartz L W,Roy R V 1999J.Colloid Interface Sci.218 309
[11]Carey E,Stubenrauch C 2010J.Colloid Interface Sci.343 314
[12]Tabakova S S,Danov K D 2009J.Colloid Interface Sci.336 273
[13]Matar O K 2002Phys.Fluids14 4216
[14]Boussinesq J 1913Ann.Chim.Phys.29 349
[15]Li T M,Jia S Y 1995CIESC J.5 532(in Chinese)[李佟茗,贾绍义1995化工学报5 532]
[16]Naire S,Braun R J,Snow S A 2000J.Colloid Interface Sci.230 91
[17]Naire S,Braun R J,Snow S A 2004J.Comput.Appl.Math.166 385
[18]Naire S,Braun R J,Snow S A 2001Phys.Fluids13 2492
[19]Heidari A H,Braun R J,Hirsa A H,Snow S A,Naire S 2002J.Colloid Interface Sci.253 295
[20]Snow S A,Pernisz U C,Nugent B M 1996Dow Corning Corporation Research Report1996-I0000-41395
[21]Lopez J M,Hirsa A H 2000J.Colloid Interface Sci.229 575
[22]Vitasari D,Grassia P,Martin P 2015Appl.Math.Model.40 1941
[23]Elfring G J,Leal L G,Squires T M 2016J.Fluid Mech.792 712
[24]Yekeen N,Idris A K,Manan M A,Samin A M,Risal A R,Tan X K 2017Chin.J.Chem.Eng.25 347
[25]Han G B,Wu J T,Xu X M 2000Acta Phys.Chim.Sin.16 507(in Chinese)[韩国彬,吴金添,徐晓明2000物理化学学报16 507]
[26]Gauchet S,Durand M,Langevin D 2014J.Colloid Interface Sci.449 373
[27]Saulnier L,Champougny L,Bastien G,Restagno F,Langevin D,Rio E 2014Soft Matter10 2899
[28]Sett S,Sinha-Ray S,Yarin A L 2013Langmuir29 4934
[29]Zang D Y,Rio E,Delon G,Langevin D,Wei B,Binks B P 2011Mol.Phys.109 1057
[30]Pu W,Wei P,Sun L,Jin F Y,Wang S 2016J.Ind.Eng.Chem.47 360
[31]Zhang C R 2007Ph.D.Dissertation(Beijing:Technical Institute of Physical and Chemistry of Chinese Academy of Sciences)(in Chinese)[张春荣 2007博士学位论文 (北京:中国科学院理化技术研究所)]
[32]Tian Y,Holt R G,Apfel R E 1997J.Colloid Interface Sci.87 1
[33]Avramidis K S,Jiang T S 1991J.Colloid Interface Sci.147 262
[34]Murai Y,Shiratori T,Kumagai I,Rühs P A,Fischer P 2015Flow Meas.Instrum.41 121
[35]Ivanov I B,Danov K D,Ananthapadmanabhan K P,Lips A 2005Adv.Colloid Interfac.114–115 61
[36]Manor O,Lavrenteva O,Nir A 2008J.Colloid Interface Sci.321 142
[37]Zhao Y P 2012Physical Mechanics of Surface and Interface(Beijing:Science Press)pp185,186(in Chinese)[赵亚溥2012表面与界面物理力学(北京:科学出版社)第185,186页]
[38]Li C X,Pei J J,Ye X M 2013Acta Phys.Sin.62 214704(in Chinese)[李春曦,裴建军,叶学民 2013物理学报 62 214704]
[39]de Wit A,Gallez D,Christov C I 1994Phys.Fluids6 3256
[40]Sakata E K,Berg J C 1972J.Colloid Interface Sci.40 99
[41]Saulnier L,Boos J,Stubenrauch C,Rio E 2014Soft Matter10 7117
[42]Lu K Q,Liu J X 2007Introduction of Soft Matter Physics(Beijing:Peking University Press)pp278,279(in Chinese)[陆坤权,刘寄星 2007软物质物理学导论 (北京大学出版社)第278,279页]
[43]Braun R J,Snow S A,Naire S 2002J.Eng.Math.43 281
[44]Karakashev S I,Nguyen A V 2007Colloid Surface A293 229
[45]Ivanov I B,Dimitrov D S 1974Colloid Polym.Sci.252 98
Synergistic e ff ects of disjoining pressure and surface viscosity on fi lm drainage process∗
Ye Xue-Min Yang Shao-Dong Li Chun-Xi†
(Key Laboratory of Condition Monitoring and Control for Power Plant Equipment,North China Electric Power University,Baoding 071003,China)
A mathematical model is established to investigate the gravity-driven draining process of a vertical thin liquid film containing insoluble surfactants when considering the synergistic eff ect of surface viscosity and disjoining pressure.Lubrication theory is used to derive a coupled equation set describing the evolution of the fi lm thickness,surfactant concentration and surface velocity.The equation set is solved numerically by the FreeFem program based on the fi nite element method.The fi lm is assumed to be supported by the wire frame at both the top and bottom,thus the mass of liquid and the mass of total surfactants are conserved in the simulation.The characteristics of fi lm evolution under the constant and variable surface viscosity are examined.Simulation results show that the surface viscosity is a crucial factor a ff ecting the fi lm drainage process.When neglecting the eff ect of surface viscosity,the fi lm surface exhibits the mobile mode,while the fi lm surface presents the rigid mode in the case of the surface viscosity considered.Increasing the surface viscosity,the rate of fi lm drainage is slowed down signi fi cantly,leading to a reduction of the fi lm thinning and enhancement of fi lm stability,which is consistent with the results obtained by Naire et al.The disjoining pressure is a key factor in the formation of“black fi lm”.When the disjoining pressure is only involved in the model,the length of the“black fi lm”region is relatively short,nevertheless,if the e ff ect of surface viscosity is only considered,a stable“black film”does not form.Under the synergistic e ff ect of the disjoining pressure and surface viscosity,a very long and thin but stable“black fi lm”is found in the middle segment of the fi lm.Additionally,the thickness of“black fi lm”increases and the appearance time postpones with the increase of surface viscosity.Considering the in fl uence of concentration-dependent surface viscosity,the drainage rate is greatly a ff ected.In the early stage,due to the smaller overall surface viscosity,the surface velocity is relatively large.With increasing surface viscosity at the bottom of fi lm,the strength of the fi lm surface tends to be enhanced,and then the anti-perturbation ability of the fi lm is promoted and the fi lm thinning is retarded.There is no signi fi cant di ff erence in the length nor the appearance time of“black fi lm” except that the thickness of“black fi lm”with concentration-dependent surface viscosity is lower than that with the constant viscosity,thus the flow stability is weaker than that with the constant viscosity.In addition,the presence of the disjoining pressure slows down the thinning of“blackest” portion of the fi lm and the surfactant concentration at this position.In the numerical results of the variable surface viscosity given by Braun et al.it is observed that the concentration of surfactant could almost be swept to clean in the top part of fi lm.That is possibly because the e ff ect of the disjoining pressure is neglected by Braun et al.It should be pointed out that the surface elasticity plays an important role in the stability of fi lm.Therefore,it is necessary to consider the e ff ect of surface elasticity in the future investigation.
fi lm drainage,disjoining pressure,surface viscosity,black fi lm
26 May 2017;revised manuscript
16 July 2017)
(2017年5月26日收到;2017年7月16日收到修改稿)
10.7498/aps.66.194701
∗国家自然科学基金(批准号:11202079)和中央高校基本科研业务费专项资金(批准号:13MS97)资助的课题.
†通信作者.E-mail:leechunxi@163.com
©2017中国物理学会Chinese Physical Society
PACS:47.61.–k,47.85.mf,47.61.fg,47.55.dk
10.7498/aps.66.194701
*Project supported by the National Natural Science Foundation of China(Grant No.11202079)and the Fundamental Research for the Central Universities,China(Grant No.13MS97).
†Corresponding author.E-mail:leechunxi@163.com

