典型半监督分类算法的研究分析
孟 岩,汪云云
(南京邮电大学 计算机学院/软件学院,江苏 南京 210000)
典型半监督分类算法的研究分析
孟 岩,汪云云
(南京邮电大学 计算机学院/软件学院,江苏 南京 210000)
近年来,大量半监督分类算法被提出。然而在真实的学习任务中,研究者很难决定究竟选择哪一种半监督分类算法,而在这方面并没有任何指导。半监督分类算法可通过数据分布假设进行分类。为此,在对比分析采用不同假设的半监督分类典型算法的基础上,以最小二乘方法(Least Squares,LS)为基准,研究比较了基于聚类假设的转导支持向量机(Transductive Support Vector Machine,TSVM)和基于流行假设的正则化最小二乘法(Laplacian Regularized Least Squares Classification,LapRLSC),并同时利用两种假设的SemiBoost以及无任何假设的蕴含限制最小二乘法(Implicitly Constrained Least Squares,ICLS)的分类效果。得出的结论为,在已知数据样本分布的情况下,利用相应假设的方法可保证较高的分类正确率;在对数据分布没有任何先验知识且样本数量有限的情况下,TSVM能够达到较高的分类精度;在较难获得样本标记而又强调分类安全性时,宜选择ICLS,而LapRLSC也是较好的选项之一。
半监督分类;数据分布;聚类假设;流行假设
1 概 述
传统的机器学习技术分为两类:监督学习和无监督学习。监督学习只利用标记的样本集进行学习,而无监督学习只利用未标记的样本集进行学习,但在很多实际问题中,有标记样本通常很难收集,而无标记样本很容易得到。例如,在垃圾邮件检测中,可以自动收集大量的邮件,却只有少量是标记的垃圾邮件;在生物学中,大量的未标记数据很容易得到,而对某种蛋白质的结构分析或者功能鉴定,可能会花上生物学家很多年的时间。因此,同时利用标记样本和未标记样本的半监督学习技术在近些年发展迅速[1-4]。
半监督分类算法利用大量的无标记样本与有标记样本一同训练,以增强分类效果。为了更加有效地利用有标记样本,提出了一些数据分布假设,常见的有两种:一种是聚类假设,分类边界穿过数据低密度区域,把数据分为几簇聚类,在一簇中的样本具有相同的标签;另一种是流行假设,充分利用数据在低维空间上的流行分布,并通过拉普拉斯图构造数据流行内在的几何结构,从而在这个图中相似的样本具有相同的标签。
几乎所有的半监督分类算法都显式或隐式地利用了这两种假设[1,4]。例如,转导支持向量机(TSVM)[5]和其他扩展方法[6-8]都利用了聚类假设。而那些基于图的半监督分类方法(graph cuts[9],label propagation[10-11])和流行正则化最小二乘法(LapRLSC)[12]都利用了流行假设。除此之外,有的方法同时利用这两种假设来增强分类效果。半监督Boosting[13-14]就是一种同时利用两种假设,并利用迭代的boosting算法[15]来增强分类效果的半监督分类方法。另一种相关的算法是正则化Boosting算法[16],它同时利用boosting框架和结合了平滑性的以上两种常用假设。上述方法都显式地利用了一种或者两种假设。后来,Jesse提出了一种不利用任何显式假设的奇异的半监督分类方法—蕴含限制的最小二乘法(ICLS)[17]。ICLS在多维情况下比全监督最小二乘法(LS)分类更加准确,且在一维情况下分类精度不会低于全监督最小二乘法。
在已提出的大量的半监督分类方法中,既有利用聚类假设和流行假设中的一种的方法,也有同时利用两种的方法,甚至不利用任何假设的方法。但是很难在真实的半监督学习任务中决定采用哪种方法或假设,先前研究者们都致力于研究能够提高分类精度的新方法[18-19],几乎没有把精力用于比较各个方法的分类效果[20-21]。针对真实的学习任务中选择何种半监督分类方法这一问题,对典型半监督分类方法进行了比较。由于半监督分类方法可以通过数据分布假设来划分种类,因此,比较了几种较典型的应用不同假设的方法。以LS为基准,比较了TSVM、LapRLSC,同时利用两种假设的半监督Boosting算法,以及ICLS在真实数据集上的分类效果。
2 半监督分类方法
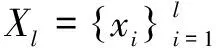
2.1转导支持向量机
聚类假设是两种常见的半监督分类假设中的一种,它假设在同一簇聚类中的样本具有相同的标签,分类边界穿过低密度区域来划分不同的簇。因此,聚类假设也被称作低密度分离假设。TSVM是利用聚类假设的半监督算法的典型代表。
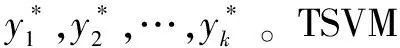
(1)
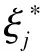
TSVM首先通过归纳式SVM在训练集上训练得到初始分类器,然后把无标记样本分为正类或负类,再根据目标函数的下降程度,转换无标记样本的类别标签,最后通过迭代的策略解决最优化问题(1)。
2.2流行正则化
另一种半监督分类学习中常用的假设是流行假设,该假设设想数据在低维服从流行分布。这个数据流行内在的几何结构通常由拉普拉斯图表示,图中的顶点代表样本,图中的边权值代表样本间的相似度。根据流行假设可知,图中相似的节点具有相同的标签。流行正则化[12,22]是基于流行假设的经典算法,该算法充分利用流行分布的几何结构,并且将数据的几何结构与数据间的相似度约束相结合,作为附加的正则化项添加到目标函数中。
LapRLSC求解一个带有最小二乘损失函数的最优化问题:
(2)

选择最小二乘损失作为损失函数,因此,正则化最小二乘法的目标函数可以写为:
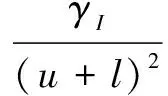
(3)
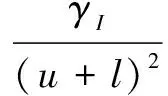
(4)
其中,α=[α1,α1,…,αn]∈RC×n为拉格朗日乘子矩阵;K为n×n的核矩阵;J=diag(1,…,1,0,…,0)为对角矩阵。
对目标函数求导,即可求得最优解。
2.3半监督Boosting
SemiBoost是一种同时利用聚类假设和流行假设,并且利用boosting框架训练分类器的半监督分类算法。用户可以选择一个偏爱的全监督分类器,然后吸收无标记样本来提升分类器的表现。对于每个无标记样本xj,分别计算对其分类为正类或为负类的置信因子,其中被当前分类器赋予置信因子最高的无标记样本标签叫做“伪标签”。在循环过程中,将这些带有伪标签的样本和有标记样本一同加入训练集来训练分类器,经历一定次数的循环后,形成最终的分类器。SemiBoost模型可以定义如下:
s.t.h(xi)=yi,i=1,2,…,l
(5)

该优化问题可以近似写成:

(6)

为了最小化该目标函数,将选取样本xi赋予的最优类别标记为zi=sign(pi-qi),选取样本的权重为|pi-qi|,并且参数α的取值应为:

(7)
初始化H(x)=0,每次迭代由全监督分类算法(LS)学习得到h(x),并且更新分类器H(x)=H(x)+αtht(x)。
2.4蕴含限制的最小二乘法
不同于以上利用一种或两种数据分布假设的半监督分类算法,ICLS不利用任何明确的假设,只利用已经存在于全监督最小二乘分类器中蕴含的假设。ICLS通过最小化一个常规的全监督分类的损失来得到最优分类器,其中全监督损失由未标记样本的所有可能标签来定义。ICLS的目标函数可以写为:
(8)
ICLS实际利用无标记样本来最小化全监督的损失函数。问题(8)的解可以看作是由全监督子集β到半监督子集Cβ的映射,可以写成如下形式:
(9)

(10)
最终,可得到关于无标记样本的最优解。ICLS在多维情况下比全监督最小二乘法分类更加准确,并且在一维情况下分类精度不会低于全监督最小二乘法。
3 实验及结果分析
3.1数据集和实验设置
数据描述:真实数据集包含了13个UCI数据集和6个基准数据集,具体描述见表1。
对于真实数据集,同样利用PCA[23]将其映射到2维空间,发现一些数据集的数据分布满足聚类假设,例如Australian、Ionosphere。还有一些数据集满足流行假设,如Digit1。另外,还有一些数据集同时满足以上两种假设,如WDBC、USPS。然而,大部分数据集的数据分布并不明确,比如Heart、Bupa、House等。
实验设置:实验中采用高斯核函数,其中高斯核的参数通过所有样本点的平均距离决定。正则化参数rA和rI固定为1和0.1,设置半监督Boosting的迭代次数为12次。
对于真实数据集的实验,采用十字交叉验证方法[24],将每个数据集随机分割为10等份,然后循环地以一组作为测试集,其余作为训练集。训练集中的有标记样本个数的选取策略与ICLS[17]相同,其中有标记样本是随机选择的,并且个数为l=max{m+5,20},m为样本特征数。将做10次十字交叉验证实验,取其平均值作为结果,实验结果见表2。

表1 真实数据集的数据分布

表2 分类错误率比较
3.2真实数据集的实验结果比较
表2列出了真实数据集上的实验结果。
根据表2,可以得出以下结论:
(1)在已知数据集的数据分布,或者能够通过PCA降维得到相应数据分布的情况下,基于相应假设的半监督分类方法表现出众。例如,对于满足聚类假设的数据集,TSVM分类效果最好,对满足流行假设的数据集,LapRLSC分类错误率最低。另外,LapRLSC在同时满足两种假设的数据集上同样有较低的错误率。
(2)当给定数据集不满足任何数据分布假设,并且强调分类安全性时,ICLS会是明智的选择。原因是ICLS分类精度不会低于全监督最小二乘法,ICLS对于无标记样本的使用不会恶化分类效果。同时,ICLS在Heart,Vehicle和Pima数据集上的分类精度是所有半监督分类算法中最高的,而LapRLSC在这些数据集上的分类精度低于全监督LS,TSVM和SemiBoost同样不能保证分类效果优于全监督算法。
(3)SemiBoost同时利用流行假设和聚类假设,并采用迭代的Boosting算法框架,但是分类效果并没有期望的出色。因此,需要在未来的工作中寻找更有效的算法来结合这些假设,并发挥它们的长处。
3.3健壮性比较
从真实数据集中选择5个数据集,在赋予不同有标记样本个数的情况下比较不同算法的健壮性。对于每个数据集,每次在训练集中随机选取5,10,20,50,100个样本赋予标记,并且采用十字交叉验证的实验设置,每组实验重复10次,取其平均值作为结果,实验结果见表3。

表3 健壮性比较
根据表3可以看出:TSVM最稳定,健壮性最好。尤其在有标记样本数目较少的情况下,TSVM是分类精度最高的算法,但其精度并没有随着有标记样本数目的增加而增加。因此,TSVM适用于给定有标记样本数目有限的情况;ICLS和LapRLSC的分类精度明显地随着有标记样本的个数的改变而改变。当有标记样本数目较少时,无论是ICLS还是LapRLSC都没有TSVM的分类精度高,但它们的分类精度随着有标记样本数目的增长而明显增长。所以,ICLS和LapRLSC适用于给定有标记样本较充裕的情况;SemiBoost无论是健壮性还是分类精度,表现都相对一般。
3.4分析讨论
观察以上实验结果,可得到一些发现,并期望给选择哪种半监督分类算法做出一些指导。
(1)在可以明确数据集的数据分布的情况下,利用相应假设的半监督分类算法能保证最好的分类效果。但在现实应用中很难得知数据的内在分布信息。
(2)若对于数据的真实分布没有任何先验知识,将很难判断哪种半监督分类算法比较适合目前的学习任务。从以上实验结果可知,在有标记样本数目较少的情况下,TSVM是分类精度最高的算法。因此,TSVM适用于给定有标记样本数目有限的情况,即使其精度并没有随着有标记样本数目的增加而明显增加。
(3)ICLS是不利用任何假设的半监督分类算法。研究者们已经证明了在假设不正确或有误差时,无标记样本有可能降低分类精度,而ICLS的分类精度却从不低于全监督LS。因此,若能获取一定量的有标记样本,并强调分类的安全性,尽管ICLS相对于全监督算法的精度提升不是那么明显(尤其是在基准数据集上),仍然是最合适的算法。
(4)LapRLSC在满足流行假设,甚至满足聚类假设的数据集上的分类效果比较令人满意。即使在某些情况下,LapRLSC的分类精度低于全监督算法,但从总体上看,LapRLSC的分类效果最好。所以当有标记样本不那么稀缺时,LapRLSC是一个不错的选择。
(5)尽管SemiBoost同时利用流行假设和聚类假设,但在以上的实验中,SemiBoost并没有令人印象深刻的表现。因此,其他更有效地利用多种假设的策略仍然值得研究。
4 结束语
大量的半监督分类方法在理论上取得了长足进展,既有利用聚类假设或流行假设其中之一的数据分布假设的方法,也有利用两种数据分布假设的方法,还有不利用任何假设的方法。因此,在真实的半监督学习任务中,采用哪种方法或者假设确实是一个难题。文中比较了利用聚类假设的TSVM,利用流行假设的LapRLSC,同时利用以上两种假设的半监督Boosting算法,以及不利用任何假设的ICLS在真实数据集上的分类效果。
实验结果表明,在已知数据分布的情况下,应该选择利用相应假设的半监督分类算法来保证获得较高的分类精度;若事先不知道样本的数据分布,并且给定的已标记样本数量有限,可以优先选择TSVM;若具有一定数量的有标记样本,并且强调分类的安全性,不利用任何假设的ICLS是比较合适的算法;另外,LapRLSC也是一个不错的选择。在真实的应用中还存在一些满足多种数据分布的数据集,将在未来的工作中寻找一种将多种假设结合的更有效的算法。
[1] Fujino A,Ueda N,Nagata M.Adaptive semi-supervised learning on labeled and unlabeled data with different distributions[J].Knowledge and Information Systems,2013,37(1):129-154.
[2] Sun S,Hussain Z,Shawe-Taylor J.Manifold-preserving graph reduction for sparse semi-supervised learning[J].Neurocomputing,2014,124(2):13-21.
[3] 梁吉业,高嘉伟,常 瑜.半监督学习研究进展[J].山西大学学报:自然科学版,2009,32(4):528-534.
[4] Zhu S P,Huang H Z,Li Y,et al.Probabilistic modeling of damage accumulation for time-dependent fatigue reliability analysis of railway axle steels[J].Journal of Rail and Rapid Transit,2015,229(1):23-33.
[5] Joachims T.Transductive inference for text classification using support vector machines[C]//Proceedings of the 16th international conference on machine learning.Bled,Slovenia:[s.n.],1999:200-209.
[6] Wang Y,Chen S,Zhou Z H.New semi-supervised classification method based on modified cluster assumption[J].IEEE Transactions on Neural Networks and Learning Systems,2012,23(5):689-702.
[7] 高 滢,刘大有,齐 红,等.一种半监督K均值多关系数据聚类算法[J].软件学报,2008,19(11):2814-2821.
[8] 李昆仑,曹 铮,曹丽苹,等.半监督聚类的若干新进展[J].模式识别与人工智能,2009,22(5):735-742.
[9] Subramanya A,Talukdar P P.Graph-based semi-supervised learning[C]//Synthesis lectures on artificial intelligence and machine learning.[s.l.]:[s.n.],2014.
[10] Ugander J,Backstrom L.Balanced label propagation for partitioning massive graphs[C]//Proceedings of the sixth ACM international conference on web search and data mining.[s.l.]:ACM,2013:507-516.
[11] 肖 宇,于 剑.基于近邻传播算法的半监督聚类[J].软件学报,2008,19(11):2803-2813.
[12] Belkin M,Niyogi P,Sindhwani V.Manifold regularization:a geometric framework for learning from labeled and unlabeled examples[J].Journal of Machine Learning Research,2006,7:2399-2434.
[13] Mallapragada P K,Jin R,Jain A K,et al.Semiboost:boosting for semi-supervised learning[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(11):2000-2014.
[14] 侯 杰,茅耀斌,孙金生.一种最大化样本可分性半监督Boosting算法[J].南京理工大学学报:自然科学版,2014,38(5):675-681.
[15] Freund Y.Experiments with a new boosting algorithm[C]//Thirteenth international conference on machine learning.[s.l.]:[s.n.],1996:148-156.
[16] Chen K,Wang S.Semi-supervised learning via regularized boosting working on multiple semi-supervised assumptions[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(1):129-143.
[17] Krijthe J H,Loog M.Implicitly constrained semi-supervised least squares classification[C]//International symposium on intelligent data analysis.[s.l.]:Springer International Publishing,2015:158-169.
[18] 李亚娥,汪西莉.一种自适应的半监督图像分类算法[J].计算机技术与发展,2013,23(2):112-114.
[19] 皋 军,王士同,邓赵红.基于全局和局部保持的半监督支持向量机[J].电子学报,2010,38(7):1626-1633.
[20] Corollary A.A comparative study:globality versus locality for graph construction in discriminant analysis[J].Journal of Applied Mathematics,2014,2014:1-12.
[21] Qiao L,Zhang L,Chen S.An empirical study of two typical locality preserving linear discriminant analysis methods[J].Neurocomputing,2010,73(10-12):1587-1594.
[22] 柯 圣.基于样本先验信息的正则化型分类器设计研究[D].上海:华东理工大学,2014.
[23] Turk M,Pentland A.Eigenfaces for recognition. J Cogn Neurosci[J].Journal of Cognitive Neuroscience,1991,3(1):71-86.
[24] Refaeilzadeh P,Tang L,Liu H.Cross-validation[M]//Liu L,Zsu M T.Encyclopedia of database systems.New York:Springer,2009:532-538.
ResearchandAnalysisofTypicalSemi-supervisedClassificationAlgorithm
MENG Yan,WANG Yun-yun
(School of Computer and Software,Nanjing University of Posts & Telecommunications,Nanjing 210000,China)
Large amounts of semi-supervised classification algorithms have been proposed recently,however,it is really hard to decide which one to use in real learning tasks,and further there is no related guidance in literature.Therefore,empirical comparisons of several typical algorithms have been performed to provide some useful suggestions.In fact,semi-supervised classification algorithms can be categorized by the data distribution assumption.Therefore,typical algorithms with different assumption adoptions have been contrasted.Specifically,they are Transductive Support Vector Machine (TSVM) using the cluster assumption,Laplacian Regularized Least Squares Classification (LapRLSC) using the manifold assumption,and SemiBoost using both assumptions,and Implicitly Constrained Least Squares (ICLS) without any assumption,with the supervised least Squares Classification (LS) as the base line.Eventually it is concluded that when data distribution is given,the semi-supervised classification algorithm that adopts corresponding assumption can lead to the best performance;without any prior knowledge about data distribution,TSVM can be a good choice when the given labeled samples are extremely limited;when the labeled samples are not so scarce,and meanwhile if learning safety is emphasized,ICLS is proposed,and LapRLSC is another good choice.
semi-supervised classification;data distribution;cluster assumption;manifold assumption
TP301.6
A
1673-629X(2017)10-0043-06
2016-10-13
2017-01-19 < class="emphasis_bold">网络出版时间
时间:2017-07-11
国家自然科学基金资助项目(61300165);高等学校博士学科点专项科研基金新教师类(20133223120009);南京邮电大学引进人才基金(NY213033)
孟 岩(1992-),男,硕士研究生,研究方向为模式识别与机器学习;汪云云,博士,副教授,研究方向为模式识别、机器学习、神经计算等。
http://kns.cnki.net/kcms/detail/61.1450.TP.20170711.1455.054.html
10.3969/j.issn.1673-629X.2017.10.010

