灰色神经网络下的多变量土壤含水量预测模型
罗党, 王浍婷
(华北水利水电大学 数学与统计学院,河南 郑州 450045)
灰色神经网络下的多变量土壤含水量预测模型
罗党, 王浍婷
(华北水利水电大学 数学与统计学院,河南 郑州 450045)
土壤含水量是评价农业墒情的重要指标,其变化规律对节水农业具有重要意义。基于土壤含水量预测问题中测量数据的特征和土壤含水量变化的内在联系,结合灰色GM(0,N)模型和BP神经网络模型的优势,构建BPSGM(0,N)模型。以河南省新郑市土壤含水量预测问题为例,基于实际测量数据,对该模型的预测值进行残差分析和关联度检验。结果表明,BPSGM(0,N)模型在土壤含水量预测方面具有良好的效果。
土壤含水量;SGM(0,N)模型;BPSGM(0,N)模型;三参数区间灰数
河南是农业生产大省,农业生产与百姓生活有着密切的联系。在农业生产中,土壤水分对农作物的影响至关重要。土壤墒情,即土壤的实际含水量,是用来指导农田灌溉的依据。针对不同时期不同区域的不同作物,结合当前作物所处的生育期,因墒灌溉,确保农作物收成是农业生产中的关键环节。目前,所有测量土壤水分的方法都必须以实际土壤为背景,不考虑其他因素,只能测量出当前土壤的含水量,无法测出未来土壤的含水量。
我国从20世纪50年代开始研究关于土壤含水量的测量问题,发展至今,研究出很多种测量方法,如烘焙法、滴定法、电容法、时域反射法等,其中烘焙法是最为常用的一种,在测量精度上具有其他方法不可比拟的优势。目前,河南省针对土壤含水量的测量问题,主要采用烘焙法测量土壤表层厚0~20 cm以及20~40 cm的土壤含水量,对每个地区设置一定数量的监测点进行测量。如对于新郑市,选取了北靳楼村等10个村的土地进行土壤采样,每个月的10号与25号左右进行土壤水分的测量。通过此种方法测量收集的土壤水分数据存在完整性和广泛性不足的问题,难以基于这些采样数据构建大样
本数据下的预测模型。
灰色系统理论主要研究少数据、贫信息系统,在少数据、贫信息的数据样本下仍可获得较高的精度。GM(0,N)模型[1-3]在实数信息下具有良好的预测效果,是目前使用较为广泛的灰色预测模型之一。GM(0,N)模型考虑到多个相关因素的影响,针对原始数据的一阶累加序列进行建模,解决了小样本数据的预测问题。
另外,影响土壤含水量的众多因素并不是一成不变的,如温度,每时每刻都在变化,实数无法完成对温度这一信息的准确表达,故可选用三参数区间灰数[4]表达原始数据,避免原始数据信息的流失。
文中将传统的GM(0,N)模型推广到三参数区间灰数信息下的SGM(0,N)模型。同时,为了更好地表达数据信息的波动性,提高模型预测精度,利用BP神经网络[5-7]对非线性拟合具有良好预测效果的优点,改进SGM(0,N)模型,构建了基于BP神经网络方法与SGM(0,N)模型的BPSGM(0,N)预测模型,并将其应用于河南省新郑市的土壤含水量预测中。
1 GM(0,N)模型、三参数区间灰数序列和BP神经网络方法
1.1 GM(0,N)模型
设系统特征行为数据序列为
相关因素序列为:
(1)
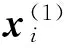

(2)

(3)
为GM(0,N)模型[8]。变量N采用灰色关联分析法[9]进行确定。
1.2 三参数区间灰数序列
设三参数区间灰数数据序列为:
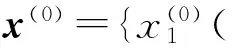
其中
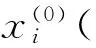

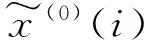
三参数区间灰数数据序列的一阶累加序列为:

(4)
1.3 BP神经网络方法
BP神经网络又称为反向传播网络[10],模拟人脑的思维方式对一组输入和输出关系进行建模,其作为一种黑箱方法,可以模拟极其复杂的关系,对于输入和输出简单、过程复杂的问题模拟得很好。一个三层的BP神经网络的拓扑结构如图1所示,该网络由一个输入层、一个隐含层和一个输出层构成,每层神经元之间全连接,同层神经元之间无连接。

图1 三层BP神经网络的拓扑结构
BP神经网络的学习主要包括利用信号正向传播和误差反向传播的两个过程,通过调整权值和阈值进行多次迭代学习,直到输出的均方误差达到要求。具体学习算法步骤如下:
步骤1初始化层间节点i与j的连接权wij和节点j的阈值θj(i=1,2,…,N;j=1,2,…,N)。
步骤2读入预处理之后的输入样本XPL和期望输出样本TPK。
步骤3通过神经元的激励函数计算各层神经元节点的输出(以第h个样本为例):
这里,Ihi既是节点i的输出,又是节点j的输入。
步骤4计算各层神经元节点的误差信号、反向传播误差、修正权值和阈值。
步骤5计算误差,重复上述步骤,直到结果落入要求的误差范围。
2 模型构建
2.1 SGM(0,N)模型的构建
设系统特征行为数据序列及其相关因素序列均为三参数区间灰数序列,由GM(0,N)模型推广到三参数区间灰数信息下的SGM(0,N)模型为:

(5)
这里因为对应的连续型求解尚无法完成,因此,考虑将模型离散化再进行求解,求解步骤如下:
步骤1数据预处理,确定构建模型所需样本数,由公式(4)求得一阶累加序列。
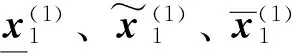
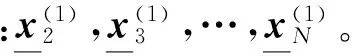

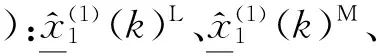
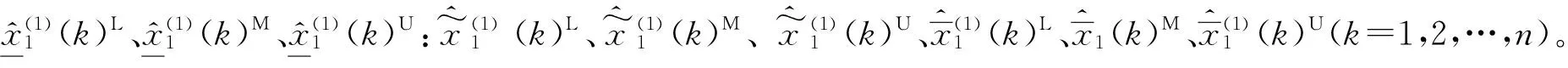
步骤7一阶累减还原得到初步预测值(以下界值序列为例):
(6)
(7)
(8)
其他值也可由此方法得到。
步骤8求得最终的预测值:
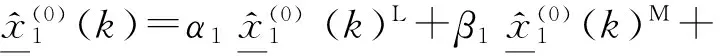
(9)

(10)

(11)
这里,αd+βd+γd=1(d=1,2,3)。其中,对于三参数区间数,中间值的指导作用要比上界值和下界值相应的指导作用大[11],因此,相关因素序列为中间值序列时,相应的预测值的权重会更大一些,由此:
β1=β2=β3>αd=γd(d=1,2,3)。
(12)
2.2 BPSGM(0,N)模型的构建
对于SGM(0,N)模型,在具体的应用问题中,公式(12)中β、α、γ的取值只能依据经验给出,会造成一定的人为影响误差。考虑到BP神经网络可以拟合任意非线性函数,但需要大量训练样本才能达到较高的预测精度这一特点,而SGM(0,N)模型能够在小样本、贫信息条件下建模并且给出较高精度的预测结果,将两者结合构建预测模型BPSGM(0,N),该模型构建过程如下:

步骤3重复步骤2,依次得到中间值序列、上界序列的预测值。
3 实例分析
3.1 研究数据
土壤含水量主要受降雨量、气温、风速、湿度以及土壤类型等因素影响[12-13]。在本文中,重点研究气象因素对土壤含水量的影响,因此在预测土壤含水量时,考虑降雨量、气温、风速、湿度这些气象因素的影响。对于这些因素,从统计学的角度来说,一段时间内的平均值是该因素最可能取到的值,而最大值和最小值则表示该段时间内该因素的值在该区间内。
对于气温和湿度,这两个因素对土壤含水量的影响属于长期影响因素,因此选取每天的平均值为基础数据集;降雨量、阵风风速则属于短期影响因素,选取每天的测量值为基础数据集,以最小值、平均值、最大值分别作为三参数区间灰数的下界值、中间值、上界值。
以研究表层厚0~20 cm的土壤含水量为例,考虑到土壤类型对土壤含水量的影响至关重要,因此选取新郑市中壤土值以及相关的气象影响因素为研究对象及影响要素,建立BPSGM(0,N)预测模型,预测土壤含水量。选取新郑市中壤土土壤含水量为系统行为指标,降雨量、气温、阵风风速、湿度为相关因素指标,2016年2—12月(1月份由于当月测量日期有降雪,因此未能测量土壤含水量)新郑地区的数据(见表1)作为原序列构建模型,预测2017年新郑地区1—5月的土壤含水量。
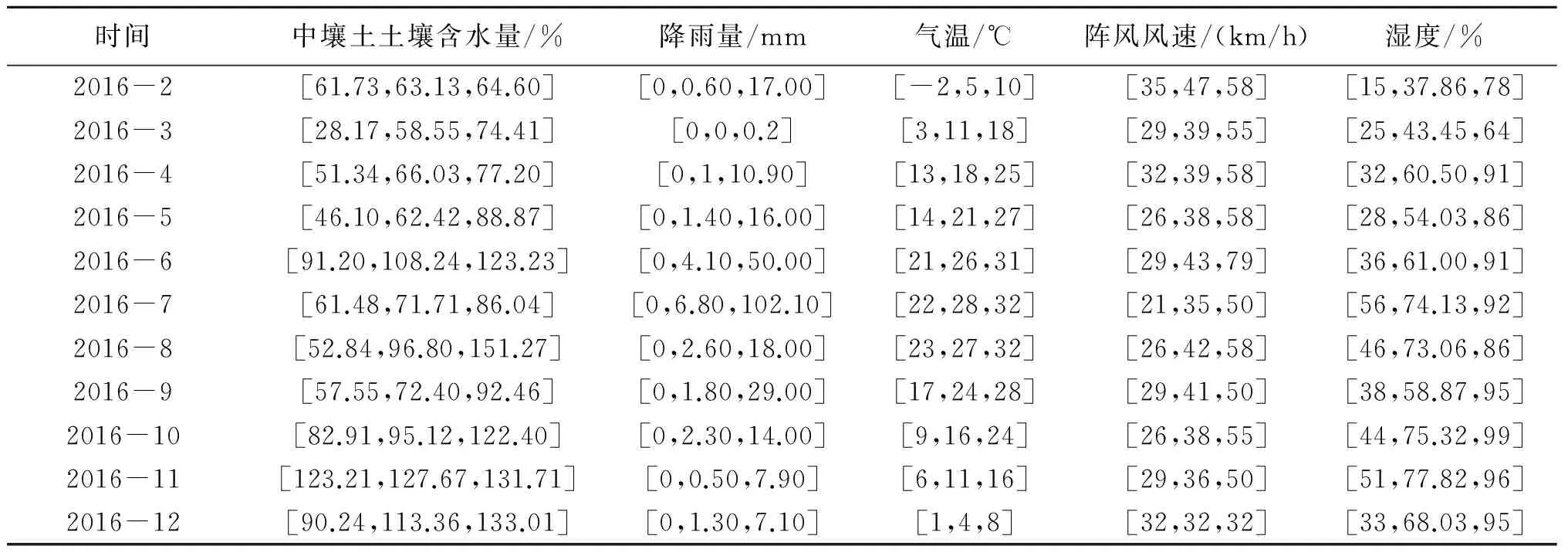
表1 2016年2—12月份指标值
3.2 BPSGM(0,N)模型的构建
利用1.1部分中GM(0,N)模型的构建方法求得的SGM(0,N)模型中各个估计值作为输入样本,相应实际值作为输出样本,构建BPSGM(0,N)模型。在MATLAB R2012b中训练神经网络时,采用三层网络拓扑结构,输入层神经元为3个,输出层神经元为1个,隐含层1层,神经元的数目由经验公式[11]
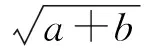
确定。其中,m为隐含层神经元个数,a、b分别代表输入层和输出层神经元的个数,β为1至10之间的整数。
3.3 预测结果
文中,输入层神经元个数为12个,输出层神经元个数为1个,根据公式求得隐含层的神经元个数应该为4~14个,反复试验。通过比较训练网络的均方误差来确定隐含层神经元个数,最终确定该层神经元个数为9个。
BP神经网络的其他参数设置如下:最小训练速率为0.2,目标误差为10-3,训练过程的最大迭代次数为50 000次。隐含层的传递函数为Sigmoid型正切函数tansig;输出层的传递函数为线性函数purelin;网络训练函数选用梯度下降BP算法函数traingd。通过反复训练,最终选择训练样本均方误差最小的神经网络得到最终预测结果,模型预测结果见表2。
根据预测值,得出2017年上半年新郑市土壤含水量的变化规律,由表2可知,土壤墒情适宜,可以结合当前月份作物对应生育期,因墒灌溉,确保农作物达到最适宜的土壤水分要求。

表2 预测结果及残差检验结果
4 误差检验
4.1 残差检验
为了更进一步说明模型预测的合理性,对模型预测结果进行了误差检验。首先将预测值与实际值相减再取绝对值得到绝对残差序列,再将得到的绝对残差值与相应的实际值相除得到残差序列:

对于预测数据来说,中间值的准确性更为重要,而最小值与最大值的准确性一样重要。因此,综合预测相对误差计算如下:
ε(k)=αεL(k)+βεM(k)+γεU(k)。
式中β>γ=α,这里取β=0.8,γ=α=0.1。
相应的综合相对误差结果列于表2中。对于BPSGM(0,N)模型,所有预测值的相对误差的平均值为10.29%,综合相对误差平均值为9.34%,均小于15%,说明所建模型的预测结果的残差检验合格。
4.2 关联度检验
关联度检验即是检验实际值与预测值曲线的相似程度。因此,选取关联度检验进一步地检验真实值与预测值之间的联系。模型得到的预测值与真实值的图像如图2所示。图2中,曲线A1、A2、A3分别代表土壤含水量真实值的上界值、中间值、下界值曲线,曲线B1、B2、B3分别代表土壤含量预测值的上界值、中间值、下界值曲线。
从图2中可以看出,两者曲线形状比较相似,但从曲线形状不能显示出两个三参数区间灰数序列之间的相似程度。使用灰色关联度计算方法,将实际值作为原始序列,预测值作为比较序列进行关联度检验。根据经验,若两者关联度大于0.6,则模型关联度检验合格。这里关联度选用基于汉明距离的三维区间灰数关联度[8],计算求得BPSGM(0,N)模型
预测值与实际值的关联度为0.875 0,两者关联度大于临界值0.6,所建模型合格。
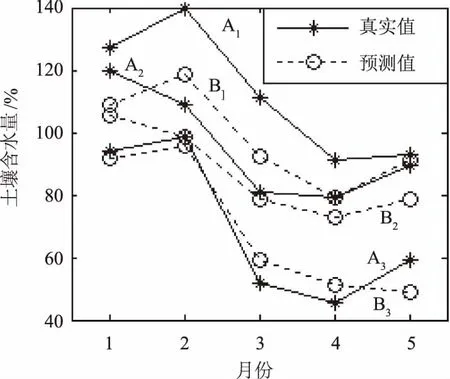
图2 真实值与预测值图像
5 情景预测
统计2005—2015年降雨量数据,只考虑1—5月份的降雨量,其中2015年为丰水年,2014年为平水年,2012年为枯水年。将2017年1—5月份的降雨量分别替换为上述3 a的降雨量,以2016年2—12月份的降水量作为原始数据,构建模型进行情景预测。预测结果见表3。

表3 情景预测土壤含水量的预测结果 %
从表3中可以看出,丰水年整体土壤墒情值偏高,平水年土壤墒情适宜,枯水年土壤墒情值偏低。这一结果说明,降雨量对土壤含水量的影响较大,这与实际情况相符。为了更好地对数据进行分析,对于三参数区间灰数,考虑到中间值提供的信息更重要,将预测得到的土壤含水量的中间值进行图像对比分析,结果如图3所示。

图3 中间值对比图
由图3可知,此预测趋势符合丰水年、平水年、枯水年的土壤含水量趋势。其中1月份和2月份土壤含水量差别不大,说明这两个月土壤含水量主要受其他因素的影响。整体上,丰水年的土壤含水量最高,平水年的次之,枯水年的最少。
6 结语
土壤含水量是影响农业生产的重要因素,是节水农业生产工作决策的参考指标。从河南省农业土壤含水量预测问题出发,针对信息为三参数区间灰数的小样本多变量预测问题,构建BPSGM(0,N)模型,并以河南省新郑市土壤含水量预测问题为例对模型进行实例验证。残差检验和关联度检验均表明模型预测结果合理,预测精度较高。由此,使用BPSGM(0,N)模型对土壤含水量进行预测是可行的。
情景预测进一步说明该预测模型的有效性,通过对土壤含水量的预测可以提前了解土壤含水量的变化规律,并进行干预,以提高区域农业干旱防御的把控能力,进而为区域农业生产决策和制订节水灌溉计划提供借鉴。
[1] 岳海晶,樊贵盛.灰色GM(0,N)模型在土壤田间持水量预测中的应用[J].节水灌溉,2016(1):19-22.
[2] 葛晨,方志耕,毕冠愚.基于GM(0,N)模型的C919价格预测[C]//第25届全国灰色系统会议论文集.北京:中国高等科学技术中心,2014.
[3] 刘凤华,谢乃明.小样本、贫信息下民用飞机费用估算模型及算法[J].系统仿真学报,2014,26(3):687-691.
[4] 罗党.三参数区间灰数信息下的决策方法[J].系统工程理论与实践,2009,29(1):124-130.
[5] 邱林,周茂,孙晗含.基于灰色神经网络模型的径流模拟与应用[J].华北水利水电学院学报,2011,32(6):26-29.
[6] 郑建安.主成分和BP神经网络在粮食产量预测中的组合应用[J].计算机系统应用,2016,25(11):274-278.
[7] 高玉明,张仁津.基于遗传算法和BP神经网络的房价预测分析[J].计算机工程,2014,40(4):187-191.
[8] 党耀国.灰色预测与决策模型研究[M].北京:科学出版社,2009.
[9] 刘思峰,邓聚龙.GM(1,1)模型的适用范围[J].系统工程理论与实践,2000,20(5):121-124.
[10] 樊振宇.BP神经网络模型与学习算法[J].软件导刊,2011,10(7):66-68.
[11] ZENG X Y,SHU L,HUANG G M,et al.Triangular fuzzy series forecasting based on grey model and neural network[J].Applied Mathematical Modelling,2016,40(3):1717-1727.
[12] 邓忠,翟国亮,吕谋超,等.我国农业应对干旱灾害的技术研究现状及展望[J].节水灌溉,2016(8):162-165.
[13] 苏欢.河南省土壤水分的时空变化特征及其与气象要素的关系[D].南京:南京信息工程大学,2015.
PredictionModelofMultivariateSoilWaterContentConstructedbytheGreyModelCombinedwithNeuralNetworkandThree-parameterIntervalGreyNumber
LUO Dang, WANG Huiting
(School of Mathematics and Statistics, North China University of Water Resource and Electric Power, Zhengzhou 450045, China)
The soil water content is an important index of evaluating soil moisture, the change law of soil water content is of great significance in water-saving agriculture. In the paper, combing the advantages of grey model GM (0,N) and BP neural network model, the model BPSGM (0,N) was constructed based on the characteristics of predicted data and the internal relation in the change of soil water content in the prediction problem of soil water content. Regarding the prediction of soil water content of Xinzheng City in Henan Province as an example, the residual value analysis and correlation test of the predicted values of the model were carried out based on the actual measurement data. The results show that the model BPSGM (0,N) can obtain good forecasting results for soil water content.
soil water content; model SGM (0,N); model BPSGM (0,N); three-parameter interval grey number
2017-06-08
国家自然科学基金资助项目(71271086);河南省科技厅重点攻关项目(142102310123);河南省高等学校重点科研项目资助计划(15A630005)。
罗党(1959—),男,河南汝南人,教授,博导,博士,从事灰色系统理论与决策分析方面的研究。E-mail:iamld99@163.com。
10.3969/j.issn.1002-5634.2017.05.009
TV93;N945.24
A
1002-5634(2017)05-0070-06
(责任编辑杜明侠)

