浅谈数形结合在数学中的应用

胡先莉 程鲁

1 绪言

一直以来，我们的数学教育都是重视数学知识的传递与教授，而轻视了数学解题思想方法的诠释与阐述。在漫长的实践历程中，人们运用各种各样的数学方法、技巧或途径来解决所遇到的问题，而在此过程中如果同一种方法、技巧或途径被反复使用了多次，并且和想象中解题的效果一致，便成为了数学方法。即对一件事物的前后状态、逻辑关系以及发展过程用数学语言表达出来，再对其进行演算和分析，以此来达到解释和预言的目的的方法就是数学方法。而数形结合的主要思想就是以代数的严谨论证为主体并以图形的直观性为辅助来加以描述探究数学问题，使得论证的过程形象具体。合理的利用数形结合这一思想来解决一些比较抽象的数学问题，可以使解题过程更加清晰明了，而数学结合的核心也可以归结为“以形助数，以数补形”八个字 。

2 数形结合的应用

2.1数形结合在函数中的应用

函数是初等数学中的重要知识，利用函数图象等数形结合解决数学问题，就是将纯粹的代数问题赋予其几何意义，实现数到形的转变，从而解决函数的最值，值域以及复合函数的定义域值域等问题。通常会采取的方法就是建立直角坐标系。

2.1.1数形结合在函数最值问题中的應用

对于函数最值问题的求法有：图象法，基本不等式法，导数法，函数法等。所以当我们遇到无法用纯代數方法解决问题时，就要考虑数形结合结合了。

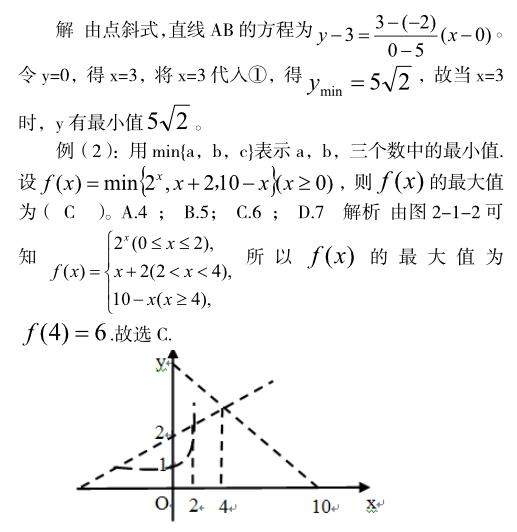
图2-1-2

解题策略：本题结合了不等式组的线性规划问题，所求f（x）为三个数中最小值中的最大值，如果单从代数角度去分析解决问题，必然会相当的复杂，但是借助图形的话，就会非常直观的看出x为何值时能取最大值。使得整个解题过程更加的清晰明了。

2.1.2数形结合在函数值域中的应用

求解函数的值域问题时如果利用数形结合的思想方法来求解无疑是将函数与图形有机地联合起来，再借助图象的形象具体性求出函数的值域。利用此方法求解的题型特点是可以从这些函数的解析式中发现某种明显的几何特征，例如直线的斜率或者是两点之间的距离公式等等，如果运用数形结合的方法来求解这些种类的函数问题，通常会更加方便容易，一清二楚。在实际生活中应用广泛。

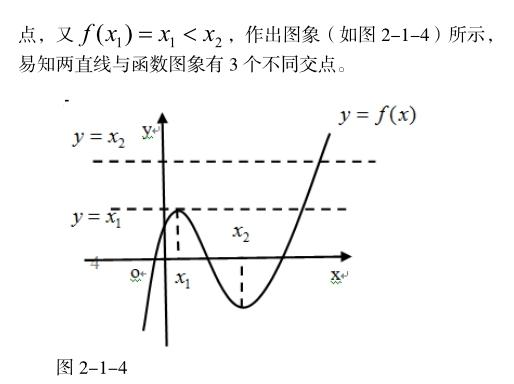
2.1.4数形结合在三角函数中的应用

三角函数的出现本来就是以几何图形为背景建立起数的概念，所以无论是在求解三角函数值还是在求三角函数的单调区间以及解析式等这类题型的时候，联系起和图形的关系都将是解题过程中不可或缺的一部分。

3 小结

本文对数形结合的特征、使用所遵循的原则、意义及其应用做了简单的讨论，对于比较抽象的数学问题通过数形结合都可以使其具体形象化。数形结合的思想是数学中基本而又重要的思想之一，它可以使人们从孤立地研究数量关系发展在变化过程中研究数量关系，使几何学代数化；用代数方法研究几何问题，同时也使某些代数问题几何化，借助几何学的成果研究解决代数问题，因而在我们的学习中，不能单纯地学习知识，而要在知识的形成过程中，随时注意渗透数形结合的思想，捕捉一切时机培养良好的思维品质。当然，在数学问题的解题中还有更多有趣的数学思想方法，还需要我们去不断地努力探索、发现。

（作者单位：成都理工大学）