最小二乘及其改进算法在外测数据处理中的应用
牟志华, 郭 枫
(解放军91550部队94分队,辽宁 大连 116023)
最小二乘及其改进算法在外测数据处理中的应用
牟志华, 郭 枫
(解放军91550部队94分队,辽宁 大连 116023)
在外测数据处理中,经典最小二乘法的使用经常出现局限性,通过引进Jacobi矩阵,讨论了多台雷达定轨的非线性加权最小二乘估计问题;对于带有先验信息的测量数据,采用Bayes估计解算飞行轨迹;为解决测量数据的设计矩阵多重相关性问题,采用有偏的岭估计公式进行轨迹推算。对于不同外测方案和各种误差特性的测量数据,应根据数据客观情况选择适宜的算法,为最小二乘及其改进算法在外测数据处理中的应用提供新思路。
最小二乘;改进算法;数据处理;Bayes估计
郭 枫(1985-),女,硕士,助理工程师。
在航区内布设测控设备对飞行器进行空间轨迹测量是飞行器外测的主要任务,外测包括光学、无线电、GPS等多种设备,这些外测设备的测量结果一般都不是直接的飞行轨迹数据,需要经过精密的数据处理加工,才能转化成飞行轨迹,供试验结果精度评定分析使用。外测数据处理的核心问题是参数估计问题,通过建立符合工程测量实际的数学模型,根据外测设备的测量数据推算模型的未知参数。文献[1]利用最小二乘法处理多星观测数据,同时进行了定姿定位的算法研究;文献[2]提出了移动最小二乘法权函数最大值的估计方法,构造了权函数的具体形式,对某航空制导炸弹飞行轨迹进行了处理;文献[3]采用最小二乘法求解测量船双站目标坐标,有效地计算了目标飞行轨迹,提高了外测数据处理精度。最小二乘估计是依据最小二乘准则,使估计量残差平方和为最小的一种估计方法,用来处理带有误差的观测数据极为有效,在外测数据处理中占有重要地位[4]。
最小二乘法的优良特性是基于观测数据的随机误差服从正态假定这个前提条件,在实际试验工程应用中,如果不满足该前提,最小二乘估计就有一定的局限性,各种改进算法应运而生,如Bayes估计、主成分估计、岭估计等[5-6],随着概率统计学和矩阵理论的发展,最小二乘及其改进方法在外测数据处理应用中得到不断完善。
1 最小二乘法概述
最小二乘法最早出现在勒让德1805年发表的论著《计算彗星轨道的新方法》附录中,勒让德描述了最小二乘法的思想、具体做法及其优点[7]。1809年,高斯发表著作《天体运动论》,他在该书末尾以极其简单的手法导出误差的正态分布,并用最小二乘法加以验证,从而使最小二乘法逐步完善化[7]。
1.1 线性模型
线性模型是最简单最直观的模型,假设有m个观测数据y1,y2,…ym与n个未知参数β1,β2,…βn,用如下方程描述
Y=Xβ+e
(1)
式中,Y为观测向量,X为观测矩阵(也称为设计矩阵),β为待估参数,e为观测子样的随机误差,其中
如果e服从正态分布,且满足等方差性、不相关的假定,即
Var(ei)=σ2,i=1,…,n,0<σ2<∞
(2)
Cov(ei,ej)=0,i,j=1,2,…,n,i≠j
(3)
则向量β的最小二乘解为[8]
(4)
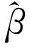
(5)
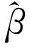
(6)
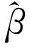
(7)
1.2 非线性模型
非线性模型用矩阵形式表示为
Y=f(X,β)+e
(8)
式中,Y,X,β,e表示同线性模型(1),但是X的含义却与之大不相同,用矩阵形式表示的非线性回归模型可以简化为
Y=f(β)+e
(9)
式中,f(β)是一个(n×1)的向量,它的每一个元素都是待估参数β的函数
(10)
当对第i个函数中的待估参数β求偏导时,可以得到一个矩阵
(11)
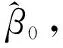
(12)
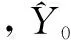
(13)
未知参数向量β的估计为[8]
(14)
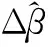
(15)
1.3 带有先验信息的Bayes估计
Bayes估计是运用Bayes条件概率公式解决实际问题的一种方法,它的一个显著特点就是在保证决策风险尽可能小的情况下,尽量应用所有可能的信息。对于线性模型(1),假设e~N(0,P),β~N(β0,V0),Bayes估计就是在给定观测数据Y的前提下估计参数β,使其估值满足
(16)
经推导β的Bayes估计为
(17)
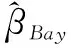
(18)

1.4 病态最小二乘问题
在线性模型(1)中,观测矩阵X的列向量之间如果近似线性相关,这种情况称为复共线性。具有复共线性的观测矩阵会导致最小二乘估计中的XTX矩阵呈现病态,也就是XTX有一个或一个以上的特征根接近于零,另外,观测数据不充分也会导致最小二乘估计中的矩阵呈现病态。当采用最小二乘估计求逆矩阵时出现病态,会导致估值不可信,为了避免病态问题,放弃无偏估计,寻找更接近真实参数值的有偏估计结果也是提高估计精度的方法[9]。有偏估计包含主成分估计、压缩估计、岭估计等,所有有偏估计中,还没有一个估计能够一致地优于其它估计,因此在试验数据处理中,应该根据测量数据特点,选择合适的估计方法。
岭估计是1962年由Hoerl首先提出的,1970年以后他与Kennard合作,对该方法做了系统的发展[9]。岭估计可以提供一个比最小二乘更稳定的解,且估计参数的标准差也比最小二乘估计的要小。对于线性模型(1),未知参数β的岭估计定义为
(19)
岭估计可以解决病态矩阵问题,在求逆之前加入常数K,就相当于使XTX的每个特征值增大了K,在一定程度上解决了病态问题。常数K反映了岭估计的偏差量,当K=0时,岭估计就是最小二乘估计,当K>0时,岭估计是有偏的估计,估计偏差随着K值的增大而增大。在解决矩阵病态方面,岭估计比最小二乘估计更稳定。
2 应用改进
2.1 多台雷达测元定轨的非线性加权最小二乘估计
在外测数据处理中,经常遇到待估参数与观测数据之间呈非线性关系的情况,例如光测设备的测量数据是方位角和高低角,某型雷达的测量数据是斜距和斜距变化率,而待估参数是发射系下飞行器的位置和速度等,显然它们之间呈非线性关系,在最小二乘求解过程中,要对非线性模型进行线性化处理。以多台雷达最小二乘定位解算为例,假设测量中采用多套雷达,每套雷达的测量数据是斜距Ri,雷达测站在发射坐标系中的坐标为xoi,yoi,zoi,测量数据Ri的测量误差为σRi(i=1,2,…n,n≥3)。
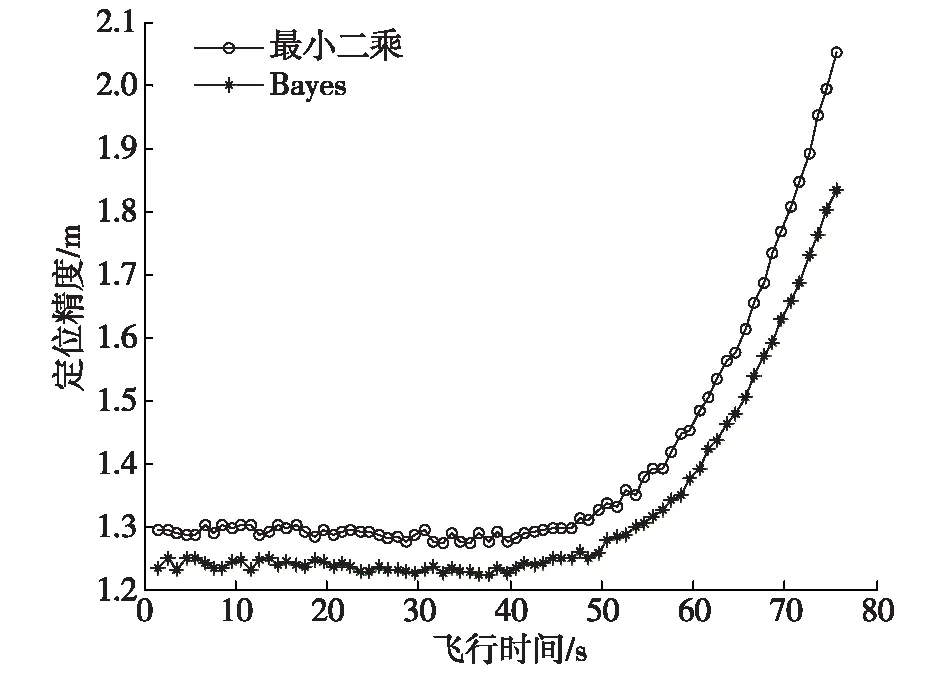
测量数据Ri与飞行器位置坐标x,y,z之间的关系式为
Ri=[(x-xoi)2+(y-yoi)2+(z-zoi)2]1/2
(20)
显然观测数据与未知参数之间是非线性关系,将方程全微分,可以得到

(21)
方程(21)可写为如下矩阵形式
(22)


ΔX=(ATP-1A)-1ATP-1dR
(23)
设坐标初值为x0,y0,z0,代入dR和A中,可以估计出ΔX的值,则新坐标参数为
(x,y,z)T=(x0,y0,z0)T+ΔXT
(24)
多台雷达nR交会求坐标采用非线性加权最小二乘估计,一般初值并不准确,经过多次迭代计算,可以比较精确地估计飞行器坐标参数。只要初始估计值在最小二乘的收敛域内,则迭代的收敛速度很快,估计结果不受初始估计值的影响;但是如果初始估计值超出最小二乘的收敛域,则迭代发散,导致最小二乘估计失败。
2.2 光学测量数据的Bayes估计
在飞行器试验的初始段数据测量中,光学测量是主要的测量手段,每台光电经纬仪测量的主要参数是方位角A和高低角E,他们都定义在观测站的垂线坐标系中。数据处理时,可以采用理论轨迹作为验前信息,根据现场试验的实际情况,假设待估轨迹上的每一点都服从以理论轨迹的坐标为散布中心,以可变的经验数据为均方偏差的三维正态分布,将理论轨迹或经验数据作为验前信息,用Bayes方法估计飞行轨迹。
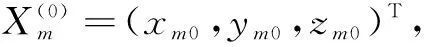
(25)

这里的均方偏差代表验前信息的可信度,均方偏差越小,表明验前信息的可信度越高,所求轨迹与验前信息越接近;均方偏差越大,验前信息的可信度就越低,对轨迹的参数估计作用也越小,此时Bayes估计就退化为最小二乘估计,在飞行器试验数据处理中,应用Bayes估计在有验前信息的条件下可以提高测量数据处理精度。
2.3 相关性测量数据的岭估计
在飞行器试验中,假设某一时间点只有两个光测站点测量到有效数据,对于飞行轨迹而言,两个站点位置较近,即两个站点与飞行轨迹的夹角比较小,此时测量参数之间表现出较强的相关性。在事后数据处理中,采用最小二乘进行无偏估计时,估计的方差较大;采用岭估计,虽然估计结果是有偏的,但估计的总误差更小一些,也更接近实际情况。岭估计能有效解决参数估计中矩阵病态问题,但对飞行轨迹上的不同时间点,由于观测站点与飞行器之间的几何位置关系不同,采用岭估计所选择的K值也不同,所以应用岭估计的关键在于选择K值。
K值的选择十分困难,它不仅依赖模型未知参数,而且这种依赖关系没有显示表示[10],一般0 在外测数据处理中,针对不同工程背景的测量数据,最小二乘有不同的应用改进算法,下面以Bayes估计为例,讨论最小二乘改进算法应用实例。当待估参数具有验前信息时,Bayes估计做为它的改进算法表现出了极大的优势。 图1 偏差5m的Bayes估计与最小二乘精度比较图 图2 偏差10m的Bayes估计与最小二乘精度比较图 在外测数据处理中,最小二乘法基于其良好的统计特性被广泛应用,但是当数据的随机误差概率分布偏离正态规律,最小二乘估计的应用就会出现局限性,为了更符合工程应用实际背景,经常采用改进的最小二乘估计。对于非线性问题,线性化处理是解决问题的良好策略,而带有先验信息的估计问题,Bayes估计的误差方差总小于最小二乘估计,当设计矩阵出现病态或者测量数据不充分时,岭估计放弃无偏性要求,可以使残差平方和更小,估计值更接近实际情况。综上所述,最小二乘法虽然有广泛的适用性,但在一些特殊的工况下,并不能取得良好的应用效果,在外测数据处理中,深入研究测量数据的误差特性,找出符合工程测量实际的改进算法是科学严谨的数据处理态度。 [1] 朱剑斌,潭守林,潭飞,等.基于最小二乘原理的天文定姿和定位方案[J].导弹与航天运载技术,2016(3):27-32. [2] 王鹏,温永强,韩云.带权重函数估计的移动最小二乘法及其在弹道处理中的应用[J].电光与控制,2016,23(3):24-27. [3] 陈红英,郭才发,向颉,等.基于最小二乘法的海基双站测量数据综合处理[J].电讯技术,2015,35(12):1413-1416. [4] 刘利生.外测数据事后处理[M].北京:国防工业出版社,2000:20-32. [5] 隋丹阳,鄂英力.线性回归模型的一种新有偏估计[J].电大理工,2015(2):22-24. [6] 张忠华.航天测量船船姿数据处理方法[M].北京:国防工业出版社,2009:64-89. [7] 王文平,朱春浩.最小二乘法:勒让德与高斯[J].武汉船舶职业技术学院学报,2011,10(6):130-133. [8] 张玉祥.线性模型参数的最小二乘估计及其改进[J].靶场试验与管理,2004(2):31-37. [9] 王惠文.偏最小二乘回归方法及其应用[M].北京:国防工业出版社,2000:67-90. [10] 张守信.航天测量数据处理[M].北京:解放军出版社,1999:203-208. The Application of Least Squares and its Improved Algorithm in Measured Data Post-processing MU Zhi-hua,GUO Feng (91550 Unit 94 Element PLA,Dalian 116023,China) The classical Least Squares algorithm is limited in measured data post-processing.This paper discusses the question of least square estimate for multi-radar nonlinear model by importing Jacobi matrix,adopts Bayes estimate for the measured data with prior information,uses ridge estimation formula to resolve design matrix multiple correlations of measured data.For different test project and measured data with all kinds of errors,fit formula should be chosen bases the factof measured data.This paper provides a new way to the application of Least Squares and its improved algorithm in measured data post-processing. least squares; improved algorithm; data processing; Bayes estimate P207;E911 A 10.3969/j.issn.1673-3819.2017.05.023 1673-3819(2017)05-0109-04 2016-12-05 2017-06-01 牟志华(1973-),女,辽宁海城人,硕士,高级工程师,研究方向为测量数据事后处理。3 仿真及应用
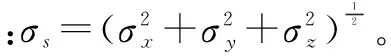
4 结束语

