电动机轴承转子多频激励系统主共振分析
李自强
(唐山职业技术学院唐山市结构与振动工程实验室,河北 唐山063000)
装备应用技术
电动机轴承转子多频激励系统主共振分析
李自强
(唐山职业技术学院唐山市结构与振动工程实验室,河北 唐山063000)
以三相异步电机轴承转子系统为研究对象,考虑转子在偏心力、轴承反力和不平衡电磁力影响。应用牛顿定律建立了电机轴承转子系统非线性振动方程。应用平均法,解析系统主共振的一次近似解和对应的定常解,并进行数值计算。分析转子偏心距、转子刚度和电磁参数等对主共振幅频响应曲线的影响。
轴承转子;电磁力;非线性振动;主共振;平均法
电动机作为驱动装置,其应用涵盖航天航空、工业、农业及日常生活等。电动机振动直接影响其运行的安全性和稳定性,电机的轴承转子系统是电机主要部件之一,其振动问题引起专家学者广泛关注。影响转子系统的非线性主要因素有:轴和支撑材料本身的非线性应力应变关系,滚动轴承刚度,油膜力,不平衡磁拉力,裂纹,间隙和碰撞等[1-3];学者邱家俊[4]著作的《机电分析动力学》对机电耦联动力学进行系统分析,并着重分析电机电磁激发参数振动及电机系统耦联非线性振动;罗跃纲[5]等应用多尺度法对具有非线性弹性的转轴共振进行分析;文献[6]采用数值仿真方法,研究轴-轴承系统非线性油膜力在不同载荷作用下的共振分析;杨志安[7,8]等研究电机轴承转子系统非线性动力学,综合考虑系统实际运行情况,建立系统在多频作用下机电藕联状态下振动方程,并利用多种解决非线性方法对系统进行解析。
本文基于文献[7]的电机转子轴承系统在多激励作用下非线性微分方程,对系统主共振进行研究,分析结构参数及材料参数对电机转子系统共振的影响,在电机的避振设计过程及运行过程产生振动的识别和预防提供理论依据。
1 转子动力学方程建立
电机转子作为绝对刚性的单盘转子(不计陀螺效应);两端由滚动轴承支承,且对转子系统形成非线性支反力;同时考虑非线性不平衡磁拉力、转子偏心力和阻尼力的作用建立永磁电机转子系统非线性微分方程:

式中,M、k、a0、Ω、E、R、L、B、u0、d、ω、Λ0= μ0/kμδ0、δ0、kμ=(k1δ0+ δF)e/k1δ0、k1、m1、m2、w1、p、Kw1、U˙+、U˙-、I˙+r、I˙-r、r1、x1、r2、x2、r2″、x2″、rm、xm分别为转子的质量、刚度、轴承支反力系数、外激频率、转子偏心、外半径,有效铁心长度、气隙磁密、真空磁导率、单边平均气隙、电网频率、平均气隙磁导、平均气隙大小、饱和度、平均气隙的计算气隙系数、铁磁材料当量气隙、定子的相数、定子的绕组匝数、定子的绕组系数、磁极对数、正序电压、逆序电压、转子正序折算电流、转子逆序折算电流、定子电阻、定子电抗、转子电阻的折算值、转子电抗的折算值、转子逆序电阻的折算值、转子逆序电抗的折算值、励磁电阻、励磁电抗。
2 主共振分析


3 数值计算与结果分析
按式(13),应用 Matlab语言可计算主共振系统的响应曲线,系统的参数选取:M=20.3 kg,μ=0.01,k= 5.95× 1011N/m,a0=5.91× 109,E=4× 10-4m,R=0.0896 m,L=0.103 m,w1=20 μ0=1.257 × 10-6H/m,kμ=1.28,σ′= 7.04 × 10-4,m1=3,r1=3.5 Ω,r2′= 4.99 Ω,μ0= 1.257 × 10-6H/m,Kw2=1,w2=0.5,m2=11,δ0=0.4 × 10-3m,Kw1=0.933.
图1左为轴承转子系统的偏心距E对幅频响应曲线振幅的影响;由于转子偏心距在运行过程中受轴承和定子限制,因此偏心距在0~4.3 mm时系统幅频响应曲线幅值随偏心距的增加而增加;图1右为具有不同刚度材质的转子幅频响应曲线,不同刚度作用下对系统的主共振曲线均有明显的变化,且轴承—转子系统的振动幅值与共振区间和振动幅值随转轴刚度的增加而增加;图2分别为不同定子电阻r1、转子电阻r2及励磁电阻rm作用下轴承—转子系统的主共振相应曲线。电阻的变化对系统的振动幅值有明显的影响,系统在电阻阻值增大的时候,系统幅频响应曲线区间变化不大,但是振动幅值随着阻值的增加反而有所降低,可见系统主共振受电磁影响不大。
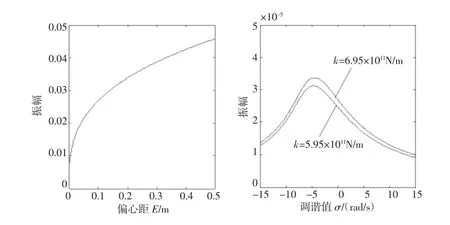
图1 随结构参数变化的响应曲线
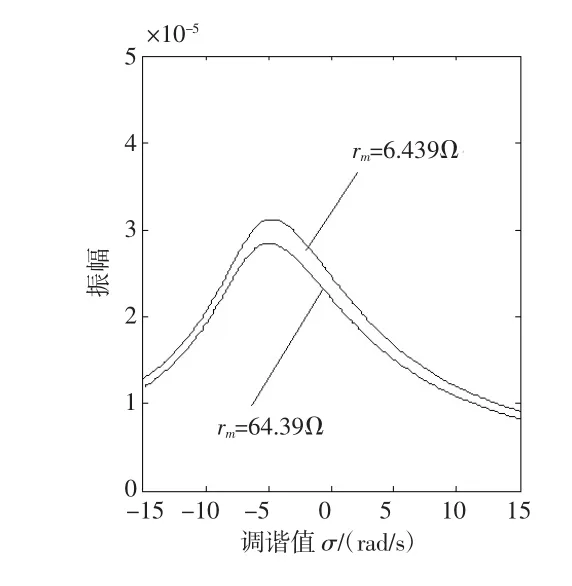
(续下图)
(续上图)
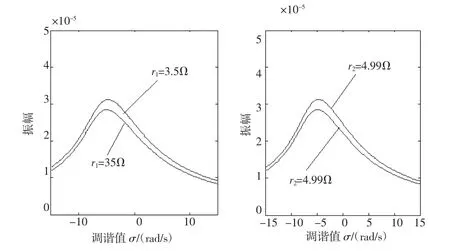
图2 随电磁参数变化的响应曲线
4 结束语
以三相异步电动机的轴承转子系统为研究对象,利用牛顿定律及机电分析动力学方法,建立电机轴承转子系统的非线性动力学方程,利用解决非线性振动的平均法解析系统在多频激励作用下的主共振一次近似解。通过二次数学变换,将系统主共振幅频响应非线性超越代数方程组转换为关于振幅与调谐参数的高次代数方程。通过数值计算得出转子偏心距对系统振动幅值影响较大,转子刚度、定子电阻、转子电阻、励磁电阻等对系统幅频响应曲线的影响也较大。此外对阻尼、气隙等因素进行分析,发现其对幅频响应曲线影响不大。研究结果对在电机的避振设计过程及运行过程产生振动的识别和预防提供理论依据
[1]焦映厚,陈照波,夏松波,等.非线性转子动力学研究现状与展望[J].哈尔滨工业大学学报,1996,31(3):1-4.
[2]Waid I.Inayat-Hussain.Nonlinear dynamics of a magnetically supported rigid rotor in auxiliary bearings[J].Mechanism and Machine Theory.2010,45(11):1651-1667.
[3]李殿起,张艳珠.永磁电动机转子非线性动力特性[J].机械强度,2004,26(2):127-131.
[4]邱家俊.机电分析动力学[M].北京:科学出版社,1992.
[5]罗跃纲,杜元虎,闻邦椿.非线性弹性转子系统动力学特性分析[J].机械设计与研究,2006,22(5):56-59.
[6]李 震,桂长林,李志远,等.变载荷作用下轴-轴承系统动力学行为研究[J].机械设计与研究,2005,21(1):12-16.
[7]杨志安,李自强.电机轴承转子多频激励系统参-强联合共振 [J].机械强度,2013,35(5):695-699.
[8]杨志安,孟佳佳.电动机轴承转子系统弱非线性主共振分析[J].机械强度,2015,37(7):13-17.
Primary Resonance Analysis of the Bearing Rotor Multi-frequencies Excitation of a Motor
LI Zi-qiang
(Key Lab of Structure and Vibration of Tangshan and Tangshan Vocational& Technical Collage,Tangshan Hebei 063009,China)
Changing a bearing rotor system of a motor as object,consider eccentric force,bearing reaction and unbalanced magnetic pull,applying newton’s law the nonlinear vibration equation of the bearing rotor system of a motor is established.By means of the averaging method,the first approximation solutions and corresponding to stationary solutions of the primary vibration of the system are obtained,and the numerical calculation is carried out.The effect of the offset and the rigidity or the electromagnetic parameter on the response curves of the primary resonance of the system.
bearing rotor;electromagnetic force;nonlinear vibration;primary resonance;the averaging method
O322;TH133
符:A
1672-545X(2017)08-0103-04
2017-05-21
河北省教育厅指导项目(编号:zc2016070);河北省自然科学基金项目(编号:A2009000997)资助
李自强(1986-),男,河北永年人,硕士,讲师,研究方向:机械设计与机电系统动力学。

