本构模型对面板堆石坝应力变形的影响

张 飞， 费文平

(1.四川大学水力学与山区河流开发保护国家重点实验室，四川 成都 610065；2.四川大学水利水电学院，四川 成都610065)

本构模型对面板堆石坝应力变形的影响

张 飞1，2， 费文平1，2

(1.四川大学水力学与山区河流开发保护国家重点实验室，四川 成都 610065；2.四川大学水利水电学院，四川 成都610065)

邓肯-张E-B模型，能考虑土体的非线性特征以及应力历史对变形的影响，比较符合土体的受力特征。理想弹塑性D-P模型是在摩尔-库伦模型的基础上考虑了静力压力的影响，广泛应用于岩体材料的模拟。堆石体是介于土体与岩体之间的一种土石混合体，其本构模型的选择一直存在较大的争议。基于APDL二次开发，将E-B本构模型成功引入到ANSYS静力分析中，与理想弹塑性D-P模型的计算成果进行对比分析，并对E-B模型的主要参数进行敏感性分析。研究成果表明：本构模型对堆石体竖向位移影响较大，但对堆石体的应力、面板应力、及面板位移影响较小；E-B模型参数中K，n以及荷载子步对面板堆石坝应力、位移的影响较大。

本构模型；面板堆石坝；应力变形特性

Abstract:Duncan-Zhang E-B model can consider the nonlinear characteristics of soil and the influence of stress history on deformation,which is in line with the characteristics of soil.The ideal elastoplastic D-P model is based on the Mohr-Coulomb model,which takes into account the effects of static pressure and is widely used in the simulation of rock mass materials.Rockfill is a mixture of soil and rock between the soil and rock,the constitutive model of choice has been a big controversy.Based on the secondary development of APDL,E-B constitutive model was successfully introduced into ANSYS static analysis,compared with the calculated results of ideal elastic-plastic D-P model,and the sensitivity of E-B model was analyzed.The results showthat the constitutive model has a great influence on the vertical displacement of the rockfill body,but it has little effect on the stress ofthe rockfill body,the stress ofthe panel and the displacement ofthe panel.The influence ofK,n and load sub-step on E-Bmodel parameters has great influence on the stress and displacement ofconcrete face rockfill dam.

Keywords:The constitutive model；panel rockfill damand stress and deformation characteristics

0 引言

混凝土面板堆石坝是以堆石为主要材料，以混凝土面板为防渗体及垫层和过渡层所组成的，在计算坝体应力变形等方面时，构成混凝土面板堆石坝的各部分材料的工程特性及所选用的本构模型对数值分析的计算成果均有重要影响。目前用于面板堆石坝静力计算的本构模型大致分为两类：其一是弹塑性模型，其二则是非线性弹性模型。其中非线性弹性模型的发展经历了漫长的历程，主要包括早期的邓肯-张的E-μ模型，随着堆石料本构性质探索内容的不断深化，该模型也越来越满足不了计算的要求；1970年邓肯等人在E-μ模型的基础上提出了E-B模型，该模型最核心的思想是把材料各种形式的变形均假定为弹性变形，经过不断改动材料的弹性参数来大致地考虑塑性变形以减小差异。由于计算中采用的回弹模量与加载模量不同，所得出的变形也不同。它的优点是使用了增量算法，局部反映了变形应力路径的影响水平。弹塑性模型主要包括早期的Drucker-Prager模型，它是1952年由Drucker和Prager共同提出的，接近莫尔-库伦屈服准则，但却是以最简略的数学模式，在土力学塑性极限设计中得到很好的应用，并被人们所熟知，这种弹塑性本构关系在岩土力学与工程中应用最广。

ANSYS软件是一个功能强大的大型通用有限元分析软件，它包括金属、混凝土等多种材料的本构模型，但尚无土工数值分析中广泛应用的邓肯-张模型，这一遗憾无疑使ANSYS软件在土工有限元分析中的应用范围和适用性受到限制。本文通过APDL参数化设计语言对ANSYS进行二次开发，在ANSYS中加入了目前广泛应用于土体的邓肯-张E-B模型，结合具体工程，用E-B模型和D-P模型进行结果对比分析。为堆石坝选取方便合适的本构模型提供参考和依据。

1 基本理论

1.1 理想弹塑性模型

D-P模型是一种理想弹塑性模型，其表达式如下：

其中参数α和k可以用土的粘聚力C和内摩擦角φ来表示：

1.2 邓肯-张弹性静力本构模型

基于ANSYS的二次开发实现面板堆石坝的邓肯-张E-B模型，该模型中弹性模量E计算见下式

式中：c为材料凝聚力；φ为材料内摩擦角；Pa为标准大气压；σ1，σ3分别为单元的大主应力、小主应力；Rf为破坏比；K为弹性模量系数；n为弹性模量指数。修正后的切线体积模量如下：

式中，Kb是体积模量系数，m是一无量纲的量，取值范围0～1.0，泊松比为

由于堆石体的强度包线有弯曲，呈非线形，故对摩尔-库伦准则中的φ角进行修正为：

关于卸载情况，E-B模型使用回弹模量Eur继续计算，回弹模量的计算表达式如下：

式中：kur为卸载模量基数；nur为卸载模量指数，且通常情况下nur≈n。当 σ1与 σ3的差值小于历史上的最大值(σ1-σ3)0，且 s低于历史上最大值s0时用Eur，否则用Et。

2 ANSYS二次开发

APDL即ANSYS参数化设计语言（ANSYS Parametric Design Language)是一种类似FORTRAN的解释性语言，可用来自动完成一些通用性强的任务，也可以用于参数化建模，为结构分析提供了很多便利。

本文根据土石坝有限元的计算原理和分析方法，在ANSYS中利用APDL技术成功的实现了土石坝非线性有限元分析。具体步骤：

（1）利用ANSYS的“生死单元”功能，杀死全部坝体单元，激活当前填筑层单元。

（2）当前填筑层单元施加重力加速度荷载9.81/nstep（nstep为荷载子步数）进行计算，调用宏命令来提取第一及第三主应力，计算每一个单元的弹性常数Et、μ、Bt等，并修改单元的材料参数。

（3）依次施加当前层的重力加速度荷载2*9.81/nstep、3*9.81/nstep，…，9.81，仿照第（2）步求解并逐步调整单元的材料参数。

（4）利用ANSYS重启动技术，重新读取参数，恢复上级荷载时的单元生死状态，再激活新填层单元，重复（2）～（3）步，利用命令PARSAV保存计算参数，直至坝体填筑完成。

（5）编写后处理的命令流，绘制应力等值线和变形等值线等。

其中，采用APDL语言编写的E-B 模型的宏命令如下：

*create,E-B.mac !创建E-B计算的宏命令

*afun,deg !角度单位用度，不是弧度

*set,Pa,1e5

*set,sigm1,- S1(i) !S1为第一主应力，拉负压正

*set,sigm3,-S3(i) !S3为第三主应力，拉负压正

sigm3=max(sigm3,0.1*Pa)

St=2*(c*cos(Fai)+sigm3*sin(Fai))/(1-sin(Fai))

S=(sigm1-sigm3)/St!应力水平

S=min(S,0.95)!应力水平最大取值

*if,St_m(i),gt,sigm1-sigm3,and,S_m(i),gt,S,then

Et=Kur*Pa*(sigm3/Pa)**n !卸荷模量

*else

Ei=k*Pa*(sigm3/Pa)**n

Et=Ei*(1-Rf*S)**2 !加荷情况的切线模量

S_m (i)=max(S_m (i),S)!保存最大应力水平

St_m(i)=max(St_m(i),sigm1-sigm3)!保存最大应力

*endif

Bt=Kb*Pa*(sigm3/Pa)**m

Mu=(3*Bt-Et)/(6*Bt)

Fai=Fail0-dFail*log10(p/Pa)

Mu=min(Mu,0.49)

mp,ex,i,Et!修改单元i的弹性模量

mp,PRXY,i,Mu !修改单元i的泊松比

mp,dens,i,idens(emat(i))

!emat(i)用于储层单元的初始材料号

mpchg,i,i!修改i单元的材料属性，

*end !结束创建宏文件

3 工程实例分析

以某混凝土面板堆石坝为例，面板采用D-P模型，堆石体分别采用E-B模型以及D-P模型来模拟，进而探究不同的本构模型对堆石体和面板应力变形的影响，从而可以选择相对更加合理的本构模型，以便于对本工程数值模拟提供指导。

3.1 工程概况

该混凝土面板堆石坝最大坝高142 m，上游坝坡1∶1.4，上游盖重坡度1∶2.5，下游坝坡1∶1.6，设三级马道，马道高程分别为3193.00 m，3223.00 m，3253 m。由盖重区、垫层区、过渡区、主堆石区、下游堆石区、排水区、面板、下游护坡等部分组成。

3.2 有限元模型

采用二维实体单元，进行堆石坝的二维有限元静力分析。图1为堆石坝结构的二维有限元计算网格图，共797个单元，834个节点。

图1 面板堆石坝的二维有限元计算图

3.3 计算参数与工况

暂不考虑构造地应力的影响，模拟堆石坝在完建工况下的位移场及应力场，分析其分布规律。正常蓄水位高程为3278 m。

堆石料分别用E-B构模型和D-P模型来模拟。根据设计单位提供的实验数据，E-B和D-P模型材料参数分别见表1和表2。

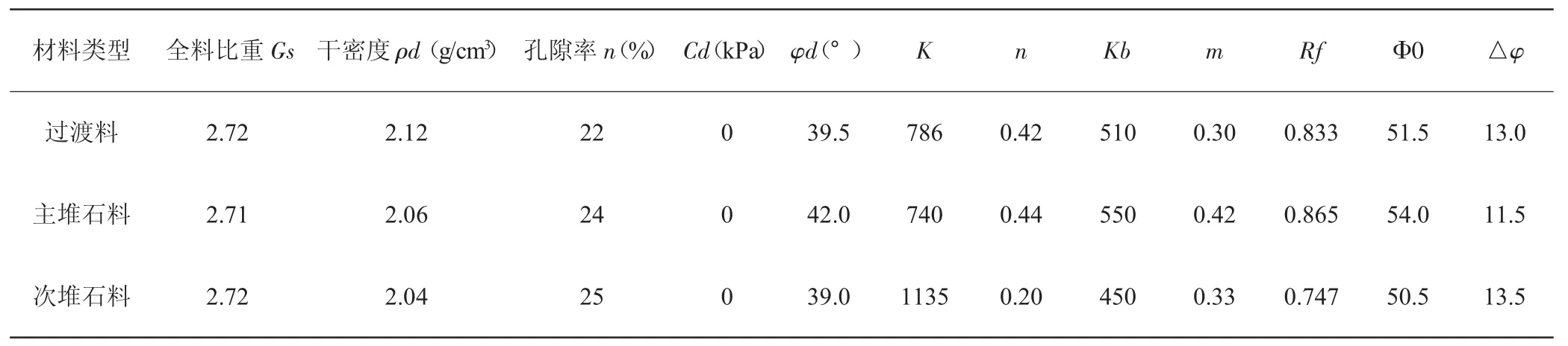
表1 E-B模型参数表

表2 D-P模型参数表

坝体计算工况仅计算完建期。计算采用生死单元模拟大坝实际填筑施工过程，坝体填筑荷载分15步施加，对比分析两种本构模型计算结果。

3.4 计算成果及对比

本次选择大坝坝体最大横断面为典型剖面进行计算分析。两种模型分析大坝坝体在完建期的应力位移情况见图2～图5，坝体及面板应力位移最大值如表3。以图2～图5中，应力拉为正，压为负，单位为Pa，堆石体水平位移指向下游为正，指向上游为负，铅直沉降向上为正，向下为负，面板法向位移指向坝体为正，偏离坝体为负，位移单位均为米。

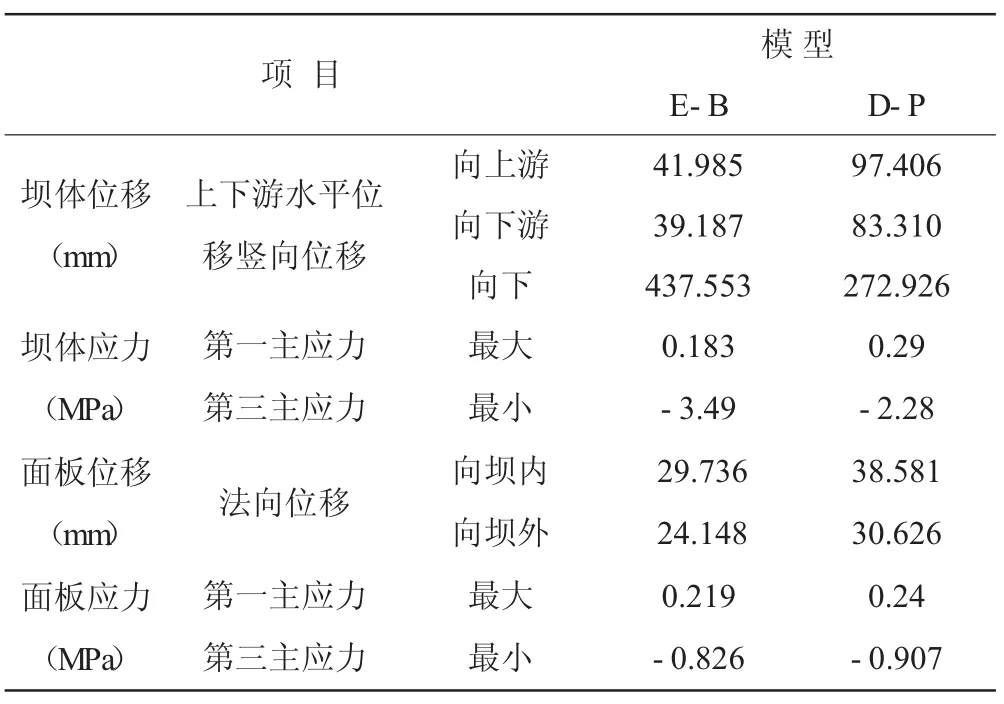
表3 坝体及面板应力、位移最大值

图2 E-B模型堆石体位移图

图3 D-P模型堆石体位移图

图4 E-B模型堆石体主应力图

图5 D-P模型堆石体主应力图

3.4.1 本构模型对应力变形结果影响分析

从图2和图3中可以看出，两种模型水平位移对称分布，发生在坝体的中下部，上下游坝坡面附近。E-B模型得出的完建期最大沉降位移为437.553 mm，约在坝体2/3高度处；D-P模型得出的完建期最大沉降位移为272.926 mm，约在坝体的中间部位。用E-B模型计算出的值要比D-P模型的值大1倍以上，这是因为坝体分层浇筑，用E-B模型模拟时，中上部的堆石体仍处于较低的应力水平，弹性模量较小，因而位移值较大。从图4和图5中可以看出，E-B模型得出坝体断面内第一主应力为0.219 MPa，发生在坝底底部中央，并且随着高程的增加，第一主应力主应力逐渐减小；第三主应力也呈现同样的分布规律，其最大值为3.49 MPa；D-P模型得出坝体断面内第一主应力为0.24 MPa，发生在坝底底部中央，并且随着高程的增加，第一主应力主应力逐渐减小，第三主应力也呈现同样的分布规律，第三主应力最大值为2.28 MPa。两种模型得出的应力分布规律大致相同，E-B模型得出坝体断面内第三主应力比D-P模型稍大，这是由于E-B模型计算过程中，其底部堆石体的弹性模量随着浇筑的进行逐渐变大，因而在坝底的第三主应力比D-P模型得到的应力值稍大。

从表3中可以看出，E-B模型得出完建期面板，向坝体内最大变形为29.736 mm，向坝体外最大变形为24.148 mm；DP模型得出完建期面板向坝体内最大变形为38.581mm，向坝体外最大变形为30.626 mm。E-B模型得出完建期面板第一主应力为0.219 MPa，面板第三主力为0.826 MPa；D-P模型得出面板第一主应力为0.24 MPa。第三主应力为0.907 MPa。在完建期由于面板的自重作用，面板浇筑后基本处于受压状态，可以得出两种模型分析结果基本符合实际情况。

3.4.2 E-B模型参数及荷载子步对堆石体应力变形结果影响分析

当参数取基准值时 (见以下各表中变化率为0相应的数值)，坝体应力位移最大值如下：堆石坝体沉降0.437 m，河流向向上游水平位移0.041 m，河流向向下游水平位移0.039 m，堆石体第一主拉应力为0.219 MPa，第三主压应力为3.49 MPa。在研究堆石坝应力变形的影响因素时发现，E-B模型参数中，K、n对堆石体应力变形结果影响较明显，如表3和表4所示；每层荷载子步数对应力变形结果影响也较明显，如图6和图7所示。

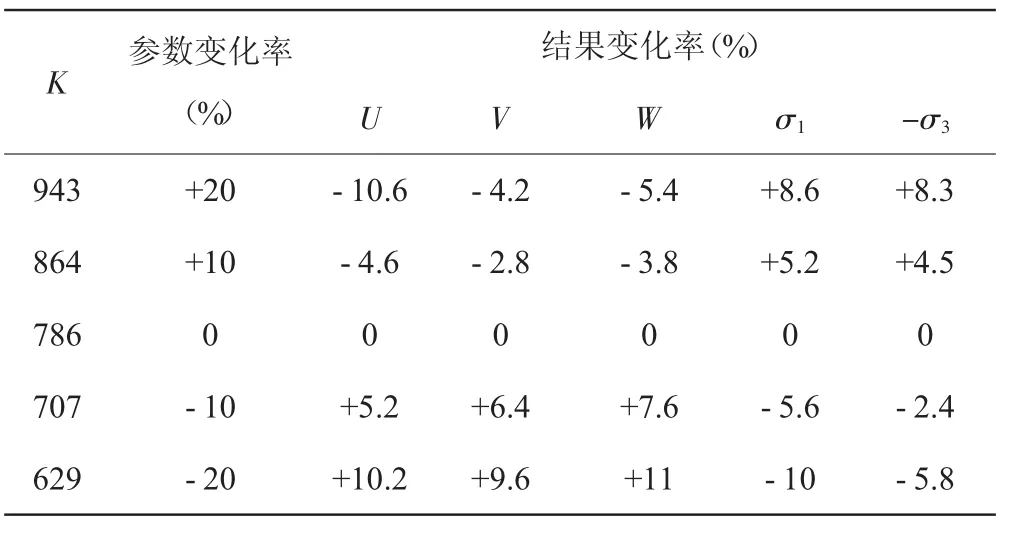
表4 参数K对应力和位移的影响

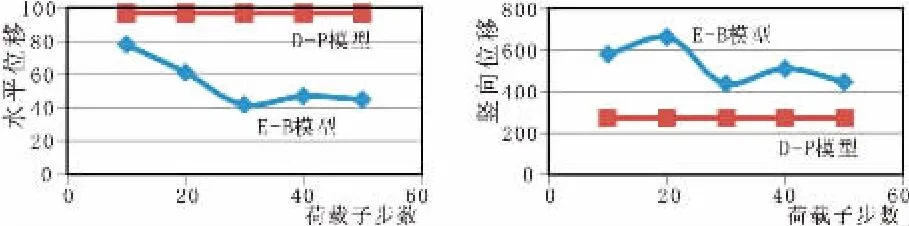
图6 荷载子步与位移关系对比曲线

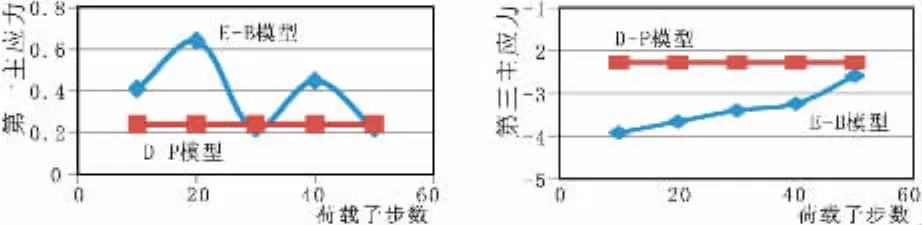
图7 荷载子步与应力关系对比曲线

从表4可知，K值变化对堆石体水平位移影响较小。K增加20%，堆石体最大沉降减小10.6%，堆石体第一主应力增大8.6%，第三主应力增大8.3%；K减小20%，坝体沉降增大约10.2%。这是由于，K值变大，相应的弹性模型在变大，则堆石体的位移变小，应力变大，反之亦然。从表5可知，当n增加20%，堆石体最大沉降减小10.8%，堆石体第一主应力增大6.2%，第三主应力增大5%；n减小20%，坝体沉降增约7.6%，堆石体第一主应力减小约8.6%，第三主应力减小约12.3%。这是由于n值变大，相应的弹性模量在变大，则堆石体的位移变小，应力变大，反之亦然。

表5 参数n对应力和位移的影响

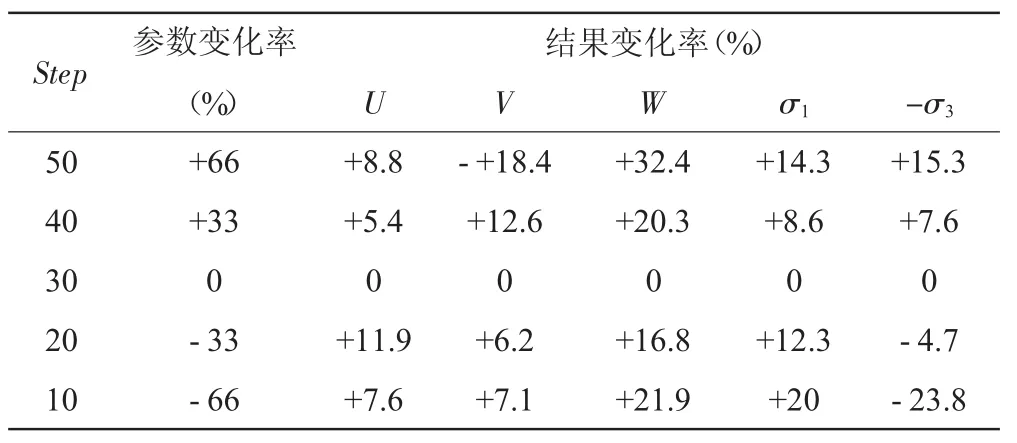
表6 荷载子步对应力和位移的影响

从表6可知，E-B模型中荷载子步变化对堆石体位移和应力影响较大。荷载子步数增加66%，堆石体最大沉降增加约32.4%，堆石体第一主应力增大14.3%，第三主应力增大15.3%；荷载子步数减小66%，坝体沉降增大约21.9%。分析结果表明：对E-B模型而言，加载历史对计算结果会产生较大影响。

4 结语

（1）由两种模型的垂直位移图看出，各个模型计算出的最大位移都在坝体的中问部位，用邓肯E-B模型时，坝体产生的最大位移处要比D-P模型偏高，约在坝体2/3高度处，而D-P模型约在坝体的中间位置。用邓肯E-B模型计算出的值要比D-P模型的值大1倍以上，这是因为坝体分层浇筑，用E-B模型模拟时，中上部的堆石体仍处于较低的应力水平，弹性模量较小，因而位移值较大。

（2）两种模型分析二维坝体完建期面板应力变形情况，EB模型得出面板的最大向坝体内变形为29.736 mm，最大向坝体外变形为24.148 mm，最大压应力为0.826 MPa。D-P模型得出面板的最大向坝体内变形为38.581 mm，最大向坝体外变形为30.628 mm，最大压应力为0.907 MPa。完建期由于面板的自重作用，面板浇筑后基本处于受压状态且面板的变形量较小。两种模型对面板应力和位移影响较小，均在工程允许范围内。

（3）E-B模型参数K、n对面板坝的应力位移影响最显著。因此，对材料参数取值时，一方面要参考类似的工程经验，另一方面通过大量室内及现场试验，反复核对参数的准确性。

[1]孙陶，高希章，杨建.紫坪铺混凝土面板堆石坝应力-应变分析[J].岩土力学，2006，（2）：247-251.

[2]Drucker D C，Prager W.Soil mechanics and plastic analysis of limit design [J].Quarterly of Applied Mathematics，1952，(10)：157-165.[8]孙明权，陈姣姣，刘运红.邓肯-张E-B模型的ANSYS二次开发及应用[J].华北水利水电学院学报，2013，（2）：30-34.

[3]顾凎臣，黄金明.混凝土面板堆石坝的堆石本构模型与应力变形分析 [J].水力发电学报，1991，（1）：13-24.

[4]吴业飞，马海霞.基于ANSYS的土石坝应力变形有限元分析[J].水利与建筑工程学报，2008，（4）：210-212.

[5]吴长彬，张岩，许小东.APDL二次开发功能在土石坝非线性分析中的应用研究[J].灾害与防治工程，2010，（1）：6-10.

Influence of the Constitutive Model on Stress and Deformation of Concrete Face Rockfill Dam

Zhang Fei,Fei Wenping

（StateKeyLaboratoryofHydraulicsand Mountain RiversDevelopmentand Protection,Sichuan University,Chengdu 610065,SichuanCollege ofWater Resources and Hydropower,Sichuan University Chengdu 610065,Sichuan）

TV641.43

A

1673-9000（2017）05-0151-04

2017-05-25

国家自然科学基金项目（51409179，51379139，51609163）

张飞（1990-），男，湖北孝感人，硕士研究生，主要从事水工结构工程研究。

费文平（1972-），男，湖北天门人，副教授，主要从事水工结构数值模拟、现场监测和室内试验研究。