分布式雷达对非合作目标弹道测量精度分析
宫志华,刘 洋,陈春江
(中国白城兵器试验中心,吉林 白城 137001)
分布式雷达对非合作目标弹道测量精度分析
宫志华,刘 洋,陈春江
(中国白城兵器试验中心,吉林 白城 137001)
针对非合作目标高精度弹道测量问题,提出采用一主三副脉冲体制分布式雷达系统组网测量模式,对系统提供的“多测距多测速”冗余测元采用基于函数约束的测元层数据融合计算方法,通过仿真计算,分析了弹道测量精度,结果表明:在合理布站条件下,如果雷达测元只含有随机误差,则弹道测量精度很高;如果测元存在系统误差,则弹道测量精度有所下降。针对消除测元系统误差,提出了4项修正内容。该文研究工作为今后作战试验条件下雷达组网测试和数据处理提供了参考。
分布式雷达;雷达组网;数据融合;信息处理;非线性函数;测量精度
Abstract:Aiming at the high-precision measurement problem for the trajectory of non-cooperative target,the network measuring model of the 1-master 3-deputies pulse-fashion distributed radar system was put forward.The measurement layer data-fusion based on function restriction was applied to the multi-range multi-velocity redundancy measurement elements supplied by this radar system.By simulation analysis,the ballistic measurement accuracy was analyzed.The results show that under the conditions of reasonable layout,the trajectory measurement accuracy is very high if the radar element contains only random errors.If the measured element contains system errors,the trajectory measurement precision declines.Four amendments to eliminate measurement system error were put forward.The research work provides reference for radar network test and data processing under the future combat training conditions.
Keywords:distributed radar;radar network;data fusion;information processing;non-linear function;measuring precision
随着现代战争的发展,以电子干扰“软”杀伤和反辐射导弹“硬”摧毁相结合的综合电子战能力的提高,特别是隐身目标、反辐射导弹、低空突防、综合电子干扰和固定式布站所组成的“五大威胁”,对现代雷达尤其是传统的单基地雷达系统构成严重威胁,而分布式雷达是对付以上威胁的重要手段,具有众多优良的特性。分布式雷达可以增加系统的生存能力,提高目标状态估计精度,增加目标状态维数,增加对弱小目标的检测概率。分布式雷达的机动性、灵活性和扩展性等技术优势可以很好地满足反导作战的跟踪与识别需求,美国已将分布式雷达技术作为美国下一代反导雷达的重要发展方向。
20世纪70年代后期到80年代初,我国开始了远程导弹的高精度试验和全程试验,对弹道测量精度提出了更高的要求,并要求对整个主动段弹道进行高精度测量。为此,我国研制建设了多套高精度连续波测量系统[1],对主动段弹道进行联合测量,该系统就是一种比较典型的特殊分布式雷达系统,在弹载(箭载)合作目标的配合下,采用“二发多收”测量形式,对导弹或火箭进行跟踪测量,实现对弹道坐标、切向速度参数高精度评估,为导弹或卫星发射试验任务的安全控制、实时引导、监控显示,载人航天任务的逃逸救生以及导弹或火箭制导系统鉴定及改进设计等提供信息支持。但该雷达系统只能对合作目标进行跟踪测量,已经不能满足今后试验与训练相结合、试验向实战化转变的新型试验模式任务需求[2]。
基于上述情况,实战化试验的特点对雷达系统的战场生存能力和目标状态评估精度等提出了更大需求,使分布式雷达系统的建设和应用成为当前研究的一个热点。本文提出一种一主三副脉冲体制的分布式雷达组网测量模式,对该雷达系统的工作模式、数据处理方法和测量精度进行了分析,为今后分布式雷达测量非合作目标提供了一种建设思路。
1 弹道参数估计模型
设计分布式弹道测量雷达系统,主要用于跟踪测量非合作目标,如图1所示,采用一主三副体制,主站雷达天线具有发射、接收功能,副站天线只具有接收功能。副站测量数据实时或事后汇于主站,由主站信息处理中心完成所有数据处理工作。

(1)

根据多源数据融合理论和靶场数据处理经验,利用这些测元值可以进行测元层融合[3],获得高精度弹道参数数据。测元层融合是指将各测量设备的测量数据集中起来,按一定准则直接融合得到最终的弹道,具有“集中式”的融合结构特点,能有效地融合测量信息,有利于提高估计的稳定性和精度,应用更科学、更广泛。
对于较长弹道参数的数据融合处理,为了提高数据融合精度和降低数据处理过程的复杂度,考虑只采用雷达的距离和速度测元进行融合处理。雷达测角系统误差的特性较复杂,不易用简洁的数学模型加以表征,工程上也不易消除;而雷达距离测元系统误差的特性简单,并且工程上易于消除;雷达速度测元系统误差非常小,可以忽略不计。综合考虑多种因素,采用“多测距多测速”思想,对于跟踪测量t时段的雷达测元数据,可以建立如下的弹道参数测量误差方程:
(2)
式中:

以下考虑如何实现对式(2)弹道待估参数的优化解算问题。依据测量冗余度ρ的概念,即测量量(样本)数量m与待估状态量数量n之间的比值:ρ=m/n,系统测量冗余度越高,对状态量估计采用一定的估计方法抵御不良数据和消除误差的影响就越好,冗余测量的存在是状态量估计提高数据精度的基础。因此,为提高测量冗余度,需要最大限度压缩弹道参数数量,即待估状态数量,通常采用函数约束的误差模型最佳弹道估计(error model best estimate of trajectory,EMBET)事后数据融合方法[3-4],其核心思想是采用某种数学函数对弹道参数进行表征,构成非线性有限元联合模型。目前,可以有效拟合逼近远射程非平稳弹道参数的函数有样条函数和Hermite函数等[5-6],这些函数的共同特点是通过对弹道时间节点的合理控制实现较长弹道不同段与段之间一定阶数的平滑连接,进而对较长弹道数据中的低频和次低频信号实现精确逼近,截断误差可以忽略不计[3]。弹道参数表征如下:
(3)
式中:b=(bxbybz),为表征函数系数;T=(txtytz),为弹道时间节点分布。
ε=Y-F(C,T)
(4)
式中:Y为各测元的各时刻测量数据形成的列向量,待估参数记为C=bT,ε为各测元的各时刻测量数据随机误差形成的列向量。

(5)


(6)
式中:记V=为多元函数关于C的梯度矩阵在处的值。
易知,依据最小二乘估计,式(6)的解为
(7)
2 仿真实例分析
基于上述分布式雷达系统设计思想和数据融合处理方法,仿真验证弹道测量精度。首先仿真计算出一条理论弹道,弹道坐标和速度与相对时间曲线如图2所示。
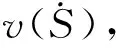

表1 分布式雷达各站测元误差分配表
设定3种雷达布站方案,总体按照星型布站模式,每种方案的主站均布设在发射阵地附近,副站按照站与站之间基线分别为50 km,100 km和150 km布设。在考虑较好的几何关系的基础上,3种布站方案分别覆盖弹道射程为70 km,130 km和200 km左右,因此,每种方案分析计算弹道长度也以此为依据。例如,基线为150 km方案中,雷达布站与弹道几何关系如图3所示。
如果不考虑系统误差的影响,则3种布站方案的弹道计算误差曲线如图4~图6所示,图中,e,ev分别为坐标和速度误差。误差统计结果如表2~表4所示,表中,μ,σ,E分别为坐标参数的平均值、均方差和总误差;μv,σv,Ev分别为速度参数的平均值,均方差和总误差。

弹道参数μ/mσ/mE/mx-0.450.070.46y0.310.230.37z0.170.060.18弹道参数μv/(m·s-1)σv/(m·s-1)Ev/(m·s-1)vx-0.0020.0260.027vy-0.0130.0530.055vz0.0020.0060.006

表3 基线100 km弹道误差统计值(无系统误差)

表4 基线150 km弹道误差统计值(无系统误差)
从上述误差统计分析结果可见,在雷达各测元只含有随机误差的情况下,针对此仿真弹道,在初始弹道段,由于弹道高度相对于各雷达站仰角较低,没有构成较好的几何关系,因此,弹道误差相对大一些,但整体弹道计算精度还是非常高,坐标定位精度可以达到1 m左右,切向速度精度可以达到0.1 m/s左右。
如果考虑测元系统误差的影响,则3种布站方案的弹道计算误差曲线如图7~图9所示,误差统计结果如表5~表7所示。

弹道参数μ/mσ/mE/mx-6.460.626.49y4.692.195.18z0.480.250.54弹道参数μv/(m·s-1)σv/(m·s-1)Ev/(m·s-1)vx-0.0200.0500.054vy-0.0860.3610.371vz-0.0070.0150.017

表6 基线100 km弹道误差统计值(有系统误差)

表7 基线150 km弹道误差统计值(有系统误差)
从上述误差分析结果可见,在雷达测元含有系统误差的情况下,在测元种类、测元数量、布站条件和计算方法等各种因素完全相同的条件下,坐标定位精度下降到10 m左右,切向速度精度下降到0.5 m/s左右。可见,参与融合计算的雷达各测元系统误差对最终弹道参数的解算影响很大,对距离测元的影响尤重。
3 结束语
从分布式雷达系统设计建设和靶场应用角度考虑,本文设想采用一主三副的脉冲分布式雷达组网模式对非合作目标进行弹道测量,并着重探讨了该系统对弹道参数测量精度的能力问题。从仿真计算结果来看,采用“多测距多测速”测元进行弹道融合计算,在雷达布站比较合理的前提下,如果不考虑测元系统误差的影响,弹道参数计算精度是非常高的;考虑测元系统误差后,弹道参数计算精度大幅下降。
因此,为满足实际工程测量需求,实现分布式雷达对非合作目标的弹道高精度测量,除尽量减小雷达系统原始测元的随机误差以外,关键问题应是如何最大限度消除雷达测元的系统误差。为此,后续应考虑在4个方面开展重点研究:①高精度电波折射修正研究;②目标跟踪部位不一致修正研究;③雷达布站优化几何关系研究;④雷达高精度标校研究。如果这些问题能够得到很好的解决,则采用分布式雷达系统对非合作目标的弹道测量是非常精确和可靠的。
[1] 李雪光.靶场高精度测速雷达系统[M].北京:国防工业出版社,2014. LI Xue-guang.High precision measuring velocity radar system in base[M].Beijing:National Defensen Industry Press,2014.(in Chinese)
[2] 李雪光.连续波反射式雷达方案设计与实现[J].导弹试验技术,2016,117(1):30-33. LI Xue-guang.The project design and realization for continuous wave reflect radar[J].Missile Test Technology,2016,117(1):30-33.(in Chinese)
[3] 郭军海.弹道测量数据融合技术[M].北京:国防工业出版社,2012. GUO Jun-hai.Trajectory data fusion technology[M].Beijing:National Defensen Industry Press,2012.(in Chinese)
[4] 王正明,易东云,周海银.弹道跟踪数据的校准与评估[M].长沙:国防科技大学出版社,1999. WANG Zheng-ming,YI Dong-yun,ZHOU Hai-yin.Tracking trajectory data calibrating and evaluating[M].Changsha:National University of Defense Technology Press,1999.(in Chinese)
[5] 宫志华,周海银,郭文胜,等.基于样条函数表征目标运动轨迹事后数据融合方法研究[J].兵工学报,2014,35(1):120-127. GONG Zhi-hua,ZHOU Hai-yin,GUO Wen-sheng,et al.Data fusion algorithm for target trajectory determination based on spline function representation[J].Acta Armamentarii,2014,35(1):120-127.(in Chinese)
[6] 宫志华,段鹏伟,岳锐,等.外弹道多源异类测元数据融合仿真分析[J].弹道学报,2014,26(4):19-23. GONG Zhi-hua,DUAN Peng-wei,YUE Rui,et al.Simulation analysis of data fusion with multi-source heterogeneous measurement elements[J].Journal of Ballistics,2014,26(4):19-23.(in Chinese)
[7] 崔书华,许爱华,赵树强,等.高精度跟踪测量系统测元数据融合处理方法[J].弹箭与制导学报,2013,33(3):167-170. CUI Shu-hua,XU Ai-hua,ZHAO Shu-qiang,et al.Fusion processing method of measurement elements in high-precision tracking measuring system[J].Journal of Projectiles,Rockets,Missiles and Guidance,2013,33(3):167-170.(in Chinese)
[8] 周海银.空际目标跟踪数据的融合理论和模型研究及应用[D].长沙:国防科学技术大学,2004. ZHOU Hai-yin.Researches on theories and models of spatial targets tracking data fusion with applications[D].Changsha:Nation University of Defense Technology,2004.(in Chinese)
AnalysisonPrecisionofDistributedRadarMeasuringNon-cooperativeTargetTrajectory
GONG Zhi-hua,LIU Yang,CHEN Chun-jiang
(Baicheng Ordnance Test Center of China,Baicheng 137001,China)
2017-05-19
宫志华(1975- ),男,高级工程师,研究方向为外弹道数据融合技术及应用。E-mail:gzh63298@126.com。
V557
A
1004-499X(2017)03-0043-06

