数学解题中妙趣横生的辩证思维

□李红春

（武汉市黄陂区第一中学盘龙校区，湖北武汉 430312）

备课参考

数学解题中妙趣横生的辩证思维

□李红春

（武汉市黄陂区第一中学盘龙校区，湖北武汉 430312）

数学是一种文化，教学过程中对学生进行辩证思维的启发和培养，使学生逐步形成一种自觉的辩证思维能力，对学生的终身发展有着重要的意义.在数学教学中，教师可以从抽象与具体、特殊与一般、繁与简、分与合、主与次、进与退、正与反、静与动、实与虚等九个方面对数学解题渗透辩证思维．

数学解题；辩证思维；数学文化

数学辩证思维是从联系、运动、发展的三个方面来考查对象，它在教学研究和数学学习中起着重要的作用，它是解决数学问题的重要策略，教学过程中教师对学生进行辩证思维的启发和培养，使学生逐步形成一种自觉的辩证思维能力，对学生的终身发展有着重要的意义.笔者结合近二十年的教学经历，从九个方面通过实例展示辩证思维在数学解题中的渗透．

一、抽象与具体

高度的抽象性是数学区别于其他学科的最显著特点之一，善于将抽象概念形象化，抽象符号具体化，抽象问题情境化，抽象方法直观化，抽象表述通俗化，可以有效降低抽象程度，减轻学生学习的难度．

例1 求证：

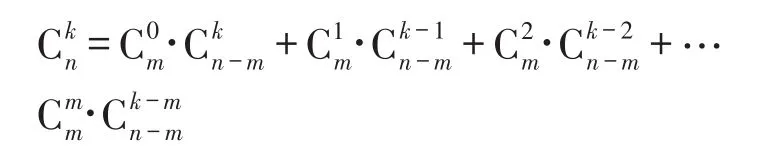
解 班上有n名学生，其中有m名男生，n-m名女生，左边表示从n名学生中选出k名学生；右边表示具体情况：若选出0名男生，则选出k名女生；若选出1名男生，则选出k-1名女生；……若选出m名男生，则选出k-m名女生．故

点评 这是一个典型的将抽象问题情境化的例子，将冰冷抽象的数学式子赋予具体的生活背景，思考起来生动形象，妙趣横生，让人难以忘怀．

二、特殊与一般

一般性寓于特殊性之中，并通过特殊性表现出来，通过特殊可认识一般．数学解题中，对特殊问题的研究、感悟、归纳、概括、提炼是解决一般问题的重要策略．

例2 设函数 f(x)满足：①对任意实数m、n都有 f(m+n)+f(m-n)=2f(m)f(n)；②对任意实数m均有 f(1+m)=f(1-m)成立；③f(x)不恒等于0，当x∈(0 ,1]时 f(x)＜1.试求的值．

解 因为 f(x)不恒为0，故存在实数x0使得 f(x0)≠0．令 m=x0，n=0，则f(x0)+f(x0)=2f(x0)f(0)，即

2f(x0)[f (0)-1]=0，因 f(x0)≠ 0，故 f(0)=1．

令m=0，n=x，则

f(x)+f(-x)=2f(0)f(x)，

而 f(0)=1，故 f(x)+f(-x)=2f(x)，

即 f(-x)=f(x)，于是 f(x)是偶函数．又f(1+m)=f(1-m)，则 f(-m)=f(2+m)，于是f(-x)=f(2+x)，因此 f(x)=f(2+x)，因此 f(x)是以2为周期的函数．那么 f(2)=f(0)=1．令m=n=1，由条件①得：

f(2)+f(0)=2[f (1)]2，所以 [f (1)]2=1，又f(1)＜1，故 f(1)=-1；令 m=n=，由条件①得：再 令得 ：而联立两式可求得：由条件②得：故

点评 本题求解如此复杂，是如何想到的？其实，首先由已知条件可联想特例f(x)=cosπx，由特例猜测抽象函数 f(x)也该有如下性质：如偶函数、有周期性、f(0)=1等，辨别哪些条件对解题有帮助，再一一从一般情况证明，基于这些性质，再将问题解决．

三、繁与简

当我们面临的是一道结构复杂、难以入手的题目时，要设法转化为一道或几道比较简单、易于解答的新题，以便通过对新题的考察，启迪解题思路，以简驭繁，解出原题．

证明：由

(a3+b3)-(a2b+ab2)=(a+b)(a-b)2≥0，

知a3+b3≥a2b+ab2，

点评 本题从整体上入手比较困难，退回局部分析，局部研究清楚后整体便不攻自破.形式上的简单，有时是思维上的复杂，形式上的复杂，有时却是思维的简单，这同样是一种智慧．

四、分与合

分类讨论是数学中重要的数学思想，很多数学问题因要考虑的情形较多，一般分开研究再综合一起，但也不能形成思维定式，有时不分反而是一种智慧．

例4 若a＞0，b＞0，则不等式-b＜1＜a

x的解集为_________.

点评 对于“连不等式”，通常是分成两个分式不等式单独求解，再取交集，本题的解答反其道而行，让人耳目一新，其中蕴含的哲理却相当深刻，数学解题要善于变通，不可思维单一．

五、主与次

“横看成林侧成峰”，不同的角度看到的问题不尽相同，解数学题要学会统揽全局，尤其是遇到多重限制条件时更要分清主次，换位思考．

例5 从6人中选出4人分别去巴黎、伦敦、悉尼、莫斯科四个城市旅游，要求每个城市有1人游览，要求每个人只游览一个城市，且这6个人中甲、乙不去巴黎，则不同的选择方案共有______．

解法1 以“人员”为主，依次考虑“甲乙都不去”“甲乙只去1人”“甲乙都去”三种情形，则有种.

解法2 以“地点”为主，依次考虑巴黎、伦敦、悉尼、莫斯科四个城市可供选择的人数，依据分步计数原理，则有N=4×5×4×3=240种．

点评 本题涉及“地点”和“人员”两个要素，分析问题时，以哪个要素为“主导”，虽然有随意性，但难易程度迥然不同．

六、进与退

数学解题就是一个不断转化的过程，将未知的转化为已知的，陌生的转化为熟悉的，形式繁杂的转化为形式简单的过程，但也不是绝对的．

例6 （武汉市2015届高三二月调考理科第10题）已知点P为曲线上任意一点，O为坐标原点，则| O P|的最小值为（ ）

解 设 P（x,y），则| OP|2=x2+y2，又xy-x-2y+3=0，于是

x2+y2=x2+y2+0=x2+y2+xy-x-2y+3=(y2+x2+1+xy-x-2y)+(x2-x+)+=(y+x-1)2+(x-1)2+≥.

点评 将简单的待求式x2+y2转化为复杂的式子x2+y2+xy-x-2y+3，然后再配方求解，以退求进，着实让人意外，乃匠心独运之作．

七、正与反

“正难则反”本质是一种“转换”的数学思想，是一种打破常规思维，采用逆向思考的解题策略，但一个问题正面的确很复杂，是否真的需要从反面入手也是充满智慧，需要因题而异的．

例7 方程x2+mx-m=0、x2+2mx-3m=0、x2+(m-1)x+m2=0至少一个有实数根，求m的范围．

解 设三个方程对应的判别式依次为Δ1、Δ2、Δ3，则

Δ1=m2+4m≥0⇔m≤-4或m≥0；

Δ2=4m2+12m≥0⇔m≤-3或m≥0；

Δ3=(m-1)2-4m2≥0∈即-1≤m≤；

设以上三个范围对应的集合为A,B,C，

取其并集得：

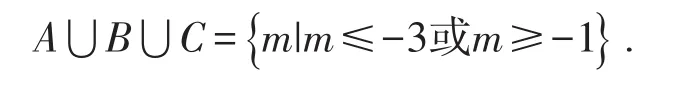
点评 本题如果不深入思考，从正面入手确实需要分7种情况讨论，因此大部分人会选择从反面入手，但如果你细心理解两个集合“并集”的概念就是指“元素至少来自其中一个集合”，你会恍然大悟．

八、静与动

唯物辩证法认为，世间万事万物都处于运动状态之中，运动是绝对的，静止是相对的，动中有静，静中有动．只有在运动的事物中寻求相对的静止，才能把握事物的本质，只有用运动的观点看待事物，才能把握事物的全貌，二者是辩证统一的关系．数学中的很多问题，就体现着这样的辩证关系．

例8 如图1，已知F1,F2分别为椭圆的左右焦点，经过椭圆上第二象限一定点P的切线为l，过原点O作OM//l交F2P于点M，则| MP|与a,b的关系是（）

A.| MP|=a B.| MP|＞a

C.| MP|=b D.| MP|＜b

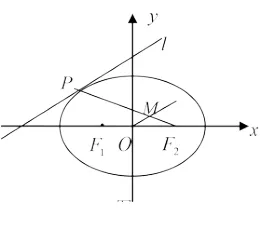
图1

图2

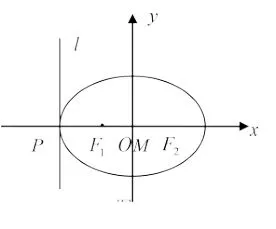
图3

分析 作为选择题，小题不大做，P为第二象限上的一定点，从运动的角度看，当P趋近椭圆上顶点时，M趋近点F2（如图2），此时即MP→a；当P趋近椭圆左顶点时，M趋近点O（如图3），此时亦有MP→a，故MP=a，选A.

点评 本题题干中指明点P为定点，为何分析时偏偏看成动点？这其中是充满智慧的，动中觅静，静中思动，以静制动，动静结合，这是数学解题中的辩证法．

九、实与虚

“虚”与“实”实际上是一对对立统一体，解题中如果一味“求实”，有时会“山穷水尽”，智慧的“就虚”有时能“柳暗花明”．

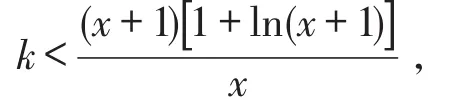
记 g(x)=x-1-ln(x+1)，(x＞0)，

点评 函数g(x)的零点客观存在，但精确值无法求出，如果一味纠结，将寸步难行，采用“虚设零点”的方法巧妙将障碍绕过去，体现“避实就虚”的思想．

数学是一种文化，数学教育的基本宗旨是实现“人”的培养，在数学解题中教会学生用辩证的思维看待问题，既能激发大家学习数学的兴趣，又能防止思维固化，提高思维的灵活性.