基于改进TLBO算法的刮板输送机伸缩机尾PID控制系统优化
胡坤,张长建,王爽,韩盛
基于改进TLBO算法的刮板输送机伸缩机尾PID控制系统优化
胡坤1,张长建1,王爽1,韩盛2
(1. 安徽理工大学煤矿安全高效开采教育部重点实验室,安徽淮南,232001;2. 香港大学电机电子工程系,香港,999077)
为了提高刮板输送机伸缩机尾控制系统的工作性能,将一种新的群智能优化算法,即教学与学习算法(TLBO)应用于机尾PID控制器的参数优化中,并提出新的自适应教学因子计算方法,其利用完整学习阶段前、后学生群体成绩的变化来决定教学因子的取值。研究结果表明:改进后的TLBO算法的精度及稳定性均比原TLBO算法的优。在建立刮板输送机伸缩机尾控制系统模型的基础上,利用改进的TLBO方法进行PID参数整定,并引入超调量控制指标对适应度函数再次完善,二次优化后的刮板输送机伸缩机尾控制系统具有良好控制品质和鲁棒性。
刮板输送机;伸缩机尾;TLBO;教学因子;PID参数优化
刮板输送机是一种由绕过机头链轮和机尾链轮(滚筒)的无极刮板链作为牵引机构的连续输送机械,它主要用于采煤工作面的运输,具有机身矮、结构紧凑,沿输送机全长可任意位置装煤,机身可弯曲且长度调整方便,机体结构强度高等优点,是目前长壁式采煤工作面唯一的运输设备。长距离、大运量、高功率的重型刮板输送机在运行时由于工作位置改变、物料特性变化、采煤机移动割煤、刮板链变形伸长等原因引起刮板链张力变化的问题日益突出,调节不即时易出现掉链、卡链、断链事故,严重影响人员安全及设备正常运行。伸缩机尾是近年来出现的一种刮板链张力调节设备,其主要功能是通过伸缩油缸推动活动机尾架以改变机尾长度(头尾链轮中心距离),以控制刮板链张力变化。它的性能直接关系到重型刮板输送机以及采煤工作面的正常运转[1]。本文作者拟对刮板带式输送机伸缩机尾PID控制系统进行建模,并利用改进的TLBO算法进行参数整定优化,以提高系统性能及稳定性,为刮板带式输送机的设计与维护提供理论参考。
1 TLBO算法及其改进
TLBO(teaching-learning-based optimization)算法,又称教学与学习算法,是由RAO等[2−3]于2011年提出的一种新型基于群体的智能优化算法。和粒子群算法(PSO)[4−5],人工蜂群算法(ABC)[6]等其他自然启发式算法模拟某个自然最优过程相类似,TLBO算法模拟教师课堂教学与学生互学的教学过程,利用教师对学生的影响,来提高学生个体水平,从而来求取全局最优解。与其他算法相比较,TLBO优化算法具有方法简单,步骤简洁,参数少,求解精度高等优点。
1.1 基本概念
对于一个维优化问题,TLBO算法的群体由一组或一班学生构成,群体规模即为学生个数;每个学生又由维设计变量组成,每维变量分别表示该学生的一门课程;学生的成绩好坏通过优化问题给定的适应度函数来进行考核;教师由目前群体中的最优解来充当。整个优化过程可分为2个阶段:教师教学阶段(学生个体向教师学习)和学生互学阶段(不同学生个体之间互相学习)。
1.2 教师教学阶段
在此阶段,教师通过教学向学生个体教授知识,学生通过向教师学习,缩小与教师之间的差距,提高全班学生的平均水平。设为当前迭代次数,其中一个学生学习前后的成绩分别为old,i和new,i,整个班级学生平均水平为M,当前学生与教师之间的水平差距为if_mean,通过差异教学努力使学生的水平提高到教师的水平teahcer,则整个教师教学过程可以由式(1)和(2)所示:
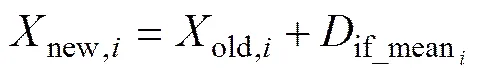
(2)
式中:r表示0~1之间的一个随机数;T为教学因子,取1或2,由式T=round[1+rand(0,1){2-1}]定义。
1.3 学生互学阶段
教师完成教学以后,学生的知识水平都有所提高,但个体水平不同,学生间仍然可通过交流讨论等方式,从其他优势个体中汲取新的知识。在学生互学阶段,学生个体X在整个群体范围内随机选择另一位学生X(≠)进行对比学习,进行对比分析后通过个体间差异进行学习调整。学生互学过程如下式所示:
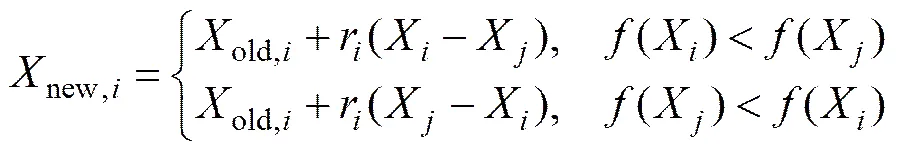
TLBO算法步骤如图1所示。
1.4 改进的TLBO算法
在标准TLBO算法计算过程中,教师教学阶段表征教师教学效果的教学因子T会在每次启发迭代时发生改变,其值由系统随机选取1或2。这使教学过程带有很大的不确定性和极端化,会造成教学效果的单一性,要么教学效果好学生全部接受教学内容,要么全盘否定,这与群体的自然多样性相悖。在TLBO的优化计算中,T过小会使低次迭代的搜索更加精细,但会使收敛速度变慢;T过大则加快搜索速度,但会降低最优化解的搜索能力。对于T的取值,RAO等[2−3]认识到教学因子T适当取值的重要性,提出了他们的见解,在一定程度上改进了TLBO算法。于坤杰等[7]提出教学因子T应当前期搜索时大,后期搜索小,并建立了随着迭代次数等差减小的T表达式T=Tmax−(Tmax−Tmin)max;TAHER等[8]认为教学因子与当前学生的平均成绩以及教师水平相关,具体数值应当为第迭代时学生群体平均值与教师的比值,即T=M/T;RAO等[9]也给出了类似的教学因子计算公式T=M/Mnew,i,其中,new,i为教学过程可使学生达到的新成绩水平,即本次迭代中教师的水平。
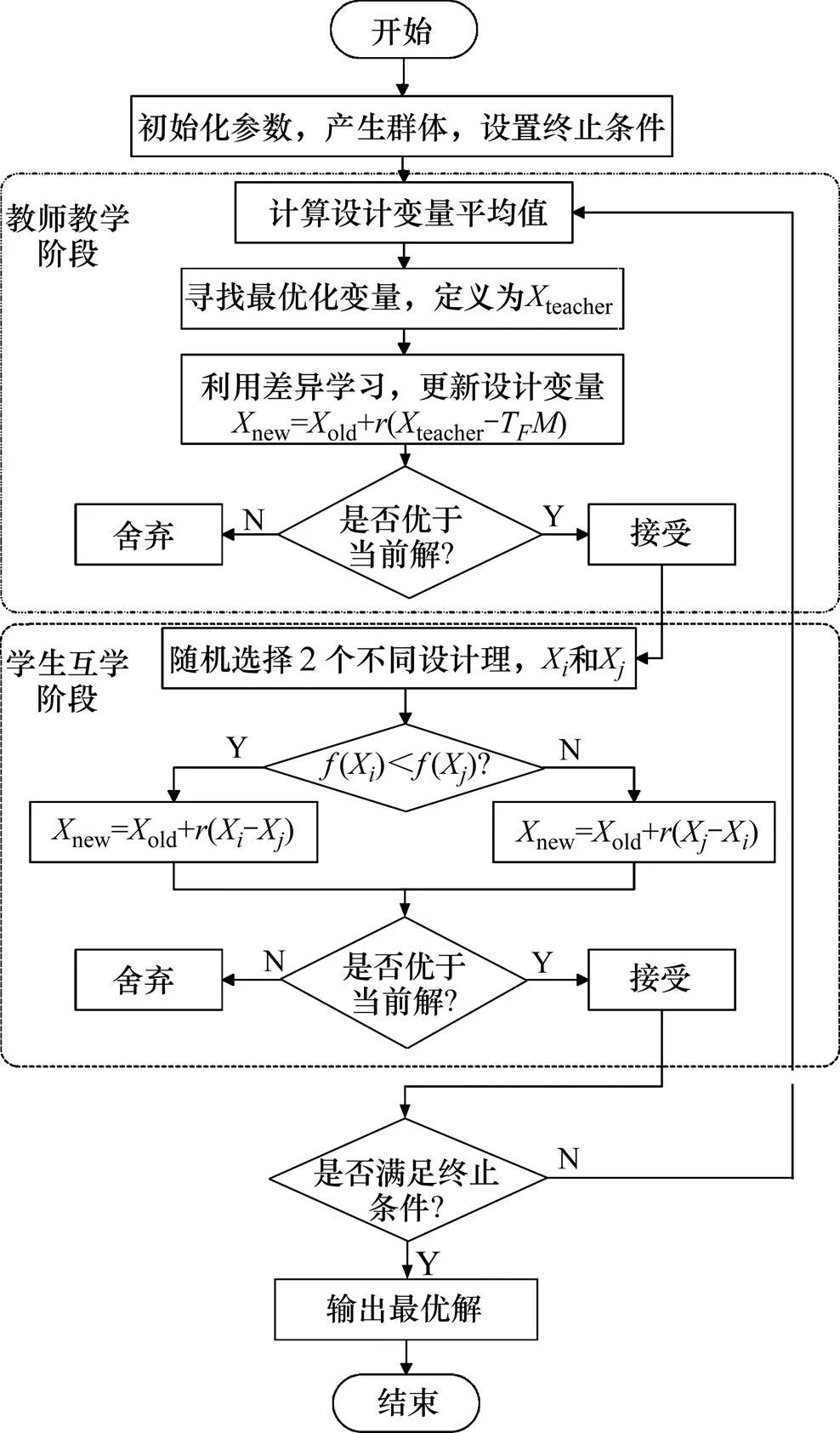
图1 TLBO流程图
在综合前人的研究的基础上,本文提出了一种新的自适应教学因子计算方法,教学因子如下式所示:
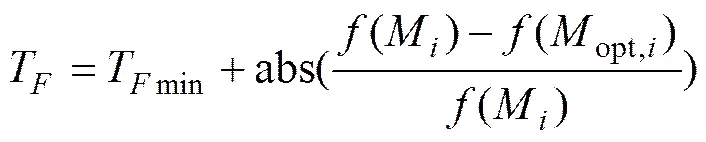
式中:opt,i为在次迭代经过教学与互学优化后,学生的平均成绩;Tmin=1;当(M)为0时,T取1。
初次迭代时,教学因子T可取最大值Tmax=2,可保证教学因子在1~2间变化。由公式可以看出,式(4)通过比较一个完整学习阶段(教学阶段和互学阶段)前、后学生群体成绩的变化来决定教学因子的取值,其成绩优劣利用评价函数()来进行判定。若优化前后评价函数变化幅度较大,则说明学生还有学习上升的空间,则选取较大的T,以加快搜索速度;若变化幅度较小,则说学生总体成绩已近最大化,优化解已接近最优值,则应当降低T进行精细搜索,保证搜索质量。
1.5 测试算例
为了验证改进TLBO算法的有效性,选取3组测试函数进行仿真,测试函数的选取包含了约束优化、无约束优化、简单二次规划以及复杂高维优化问题,如表1所示。设置群体数目P=10,教学因子最大值Tmax=2,最小值Tmin=1,1和2迭代数为150次,高维函数3迭代数为1 000次。每个函数都分别运行30次,然后求取其最优值、平均值及标准差,并与标准TLBO算法,以及粒子群算法(PSO)进行对比,比较结果如表2所示。
由表2可知:改进的TLBO算法和原TLBO算法一样,可以以较少的迭代次数快速地逼近优化问题的最优解,并且解的精度及稳定性均比原TLBO算法的优,达到了提高求解质量的预期目标。此外,对于高维复杂优化问题3,改进的TLBO算法仍然达到了较好的优化水平。由于初始群体数较小,P=10,PSO算法经过1 000次迭代计算后没有收敛;待加大群体数目P,增加迭代次数后,PSO算法也达到了较高的求解精度。

表1 测试函数
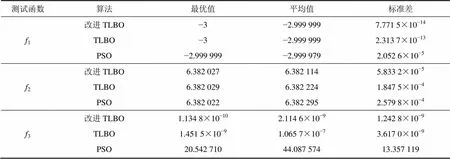
表2 测试结果比较
2 刮板输送机伸缩机尾控制系统优化
2.1 系统模型的建立
刮板输送机伸缩机尾系统主要由活动机尾架、液压缸、尾部链轮、张力传感器、液压控制系统及电气控制系统等部分组成,其简化模型如图2所示。
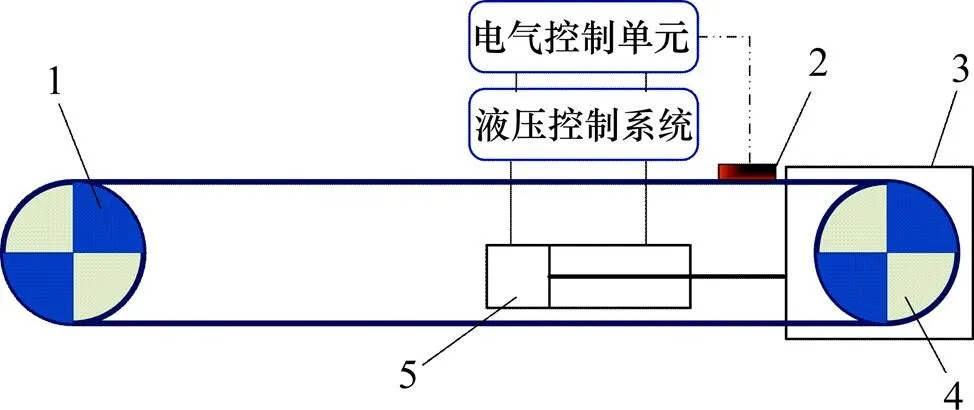
1—头部链轮;2—张力传感器;3—活动机尾架;4—尾部链轮;5—液压缸。
根据液压传动知识可知式(5)~(7)这3个相关方程。
控制阀的线性化流量方程为
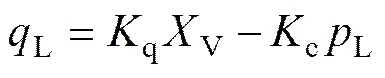
式中:q为流量增益;V为控制阀阀芯位移;c为流量压力系数;L为液压缸压力。
执行机构液压缸的流量连续性方程可表示为
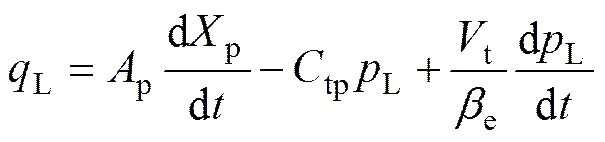
式中:p为液压缸进油腔活塞的有效面积;p为活塞位移;tp为液压缸内、外泄露系数之和;t为进油腔容积;e为有效体积弹性模量。
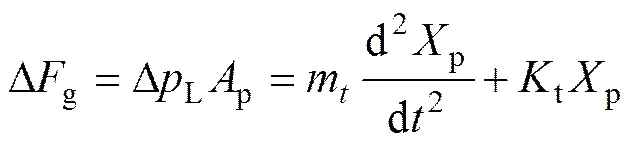
式:t为系统等效总质量;t=1.2,为刮板链刚度系数。
对式(5)~(7)进行拉氏变换,可得
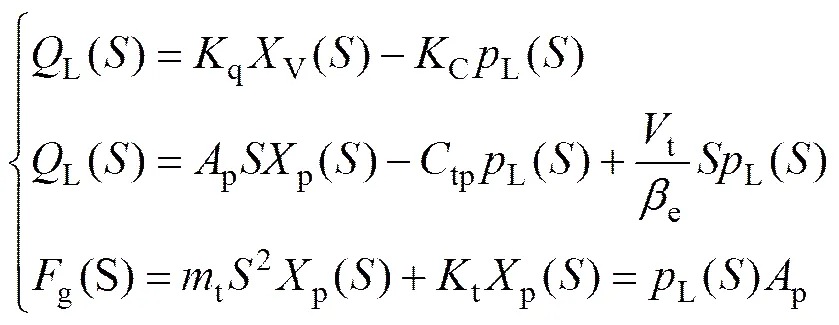
对式(8)进行化简,令ct=c−tp,可得刮板输送机伸缩机尾的传递函数:
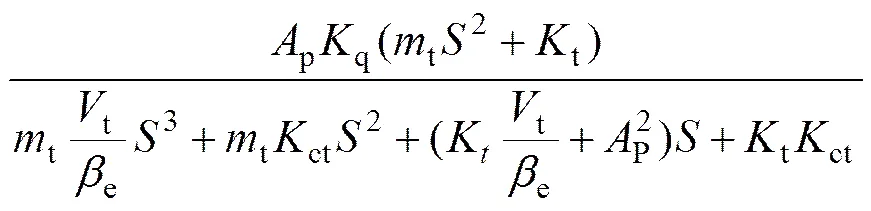
查阅相关资料[10−12],代入具体模型参数后可得
(10)
为了提高刮板输送机伸缩机尾系统性能,加入PID控制环节,并对系统进行校正,其控制系统模型如图3所示[13]。
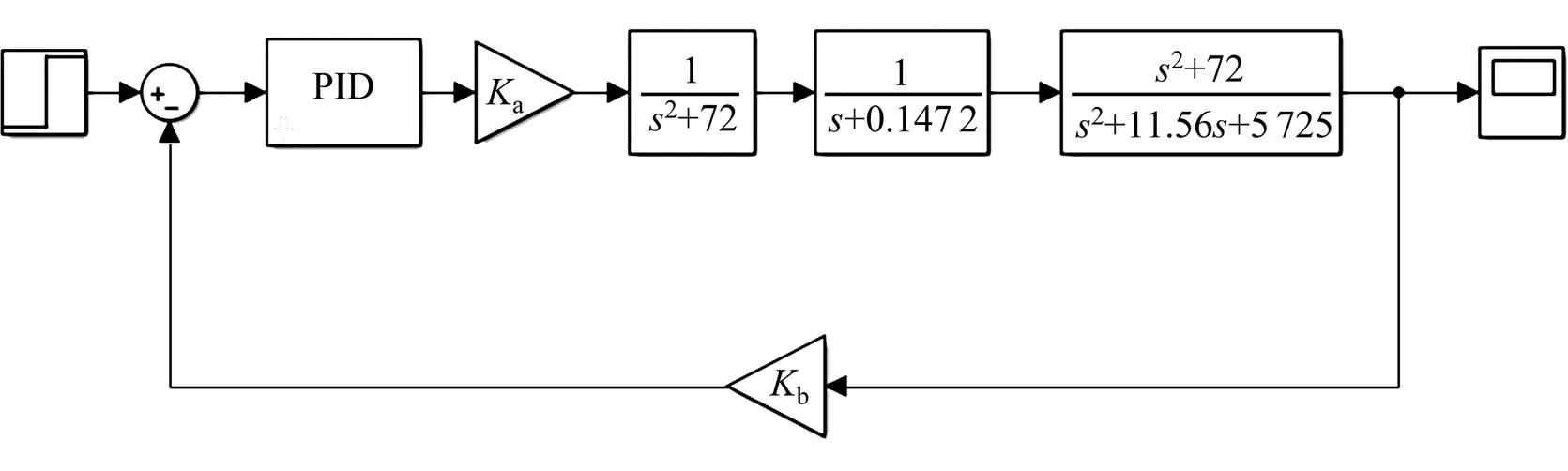
图3 控制系统SIMULINK模型
2.2 PID参数优化与仿真
1.创新高校办学培养模式,专业技术与创业能力相结合。高校鼓励大学生创新精神的不断提升需要与大学生自身的专业能力相结合,大学生的专业培养是进行了社会细分,根据某一种能力进行专门的培养,而创新创业的能力培训也单单是为了培养大学生的某一种谋生手段。高校在大学生创新能力的培养过程中,应该与其专业能力相结合,让学生在学习创业技能的同时将自身的专业知识和兴趣结合起来,发挥他们更大的创造力和创新性。将创新创业能力结合到专业能力的培养中,也使得专业技能具有最大程度的价值,不脱离社会。
利用改进的TLBO方法对PID控制器的p,i和d3个参数进行整定优化[14−15]。选用常用的PID参数整定性能指标ITAE来构成适应度函数,
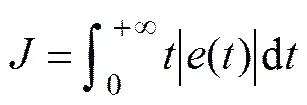
则所求适应度函数即为min。对ITAE指标进行离散化处理,设时间,为一足够大的正整数,则连续时域内的ITAE可化简为
(12)
式中:();=1, 2, …,。
利用改进的TLBO方法进行迭代计算,设置搜索范围[0.01 100],群体数目P=30,进行50次迭代后,可得PID控制器参数分别为p=76.090 0,i=51.023 2,d=91.554 7,其阶跃响应下的系统超调量为58%,迭代过程如图4(a)所示。
为了进一步改善系统性能,引用系统超调量做为辅助指标来构新的适应度函数:
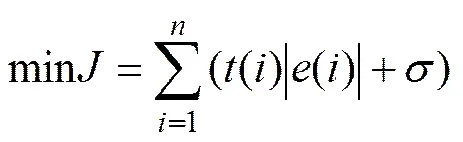
计算条件及设置不变,再次进行计算,可得p= 58.553 4,i=44.127 8,d=97.616 9 ,其阶跃响应下的系统超调量为1%。迭代过程如图4(b)所示;2次优化的计算结果如表3所示。
由图4可以看出:用改进后的TLBO算法进行PID优化时初始阶段最优值下降速度快,并快速达到收敛;后期最优值变化平缓,教学因子T变化相应减慢,有助于提高优化质量。
将适应度函数改进前后的计算结果分别代入PID系统中,进行仿真分析,其系统阶跃响应曲线如图5所示。
由图5可知:经过PID整定后的伸缩机尾控制系统能迅速对单位阶跃信号进行响应,在经历几次振荡后,于1.1 s处达到稳态;引入超调量做为辅助优化指标后,系统的超调量得到明显改善,体现了机尾控制系统的良好控制品质和鲁棒性。
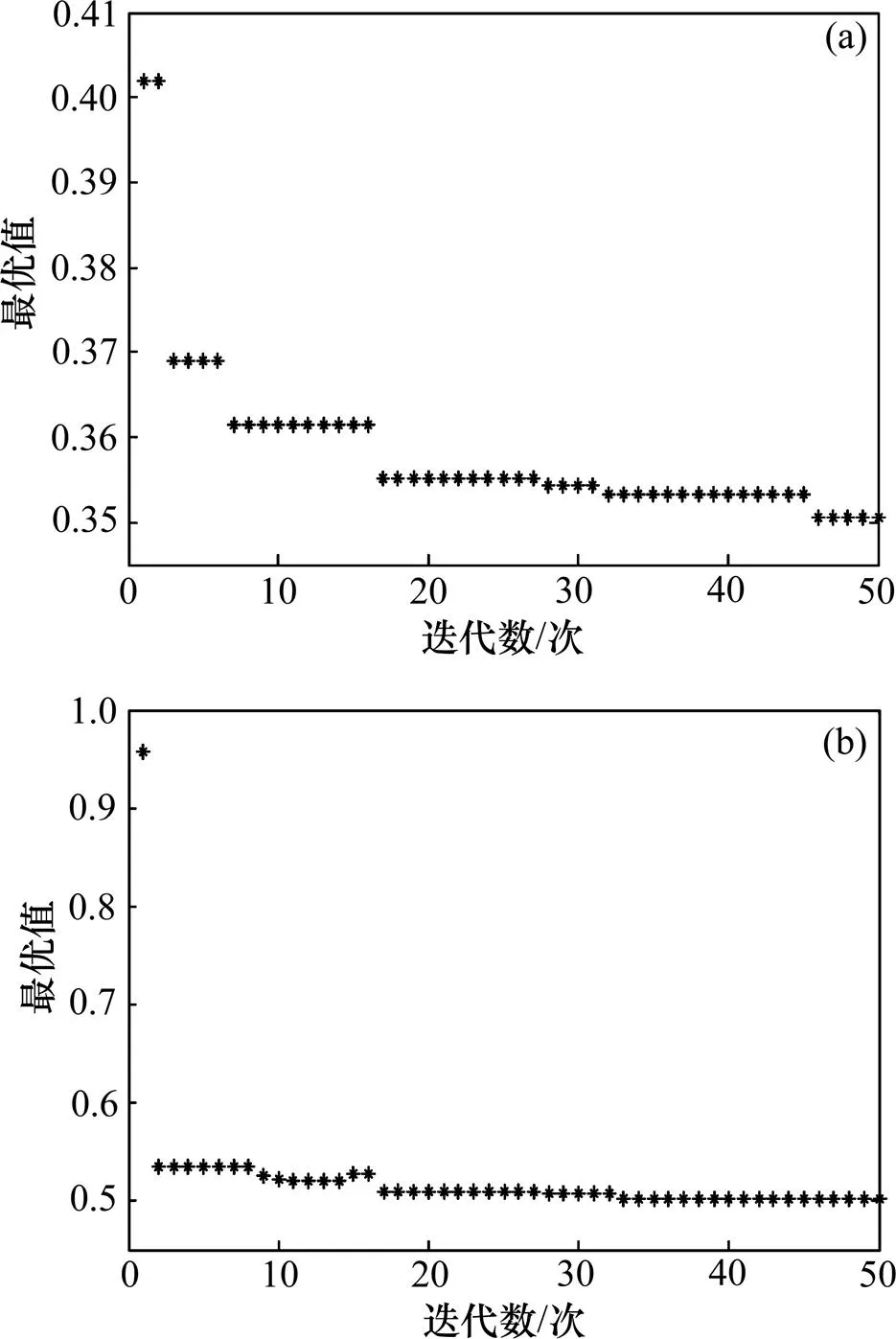
(a) 原优化迭代过程;(b) 引入超调量后迭代过程
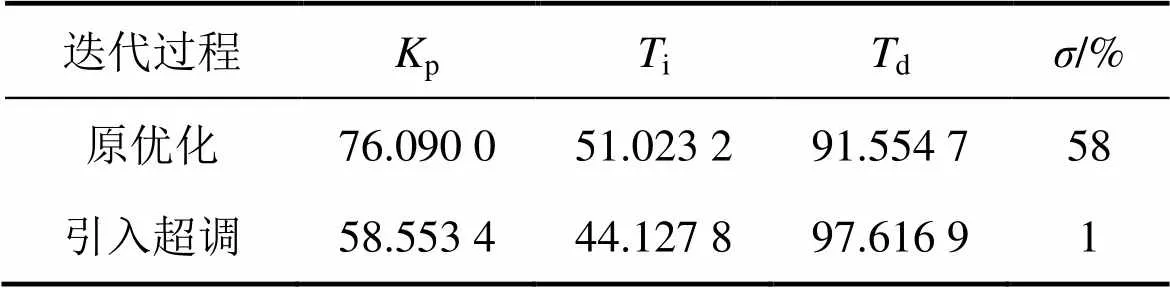
表3 优化结果比较
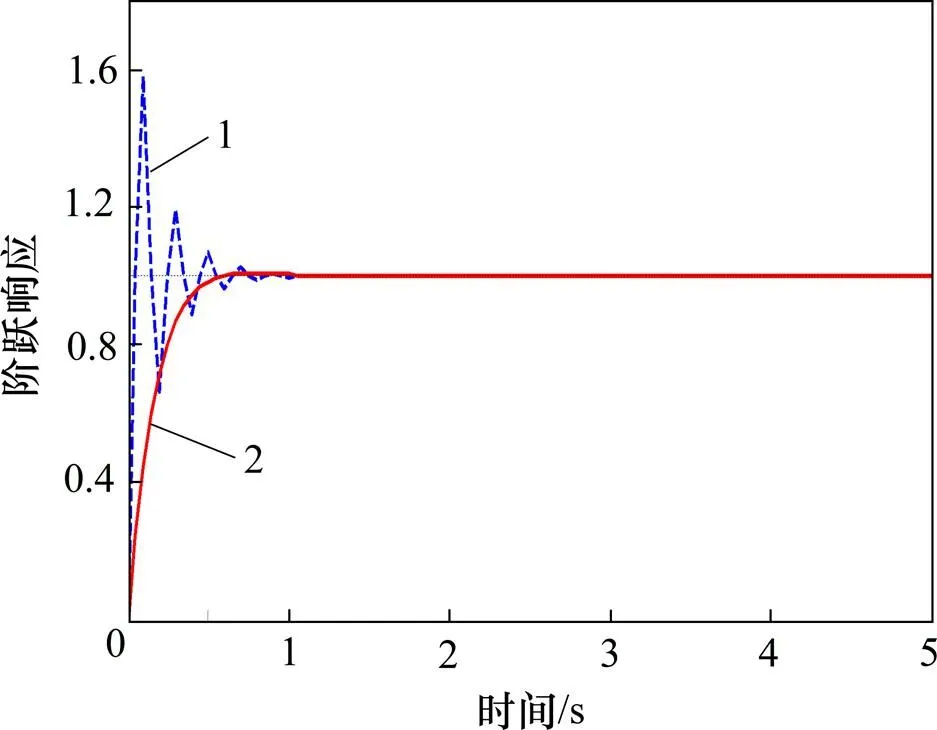
1—原优化方案的阶跃响应;2—引入超调量后的系统阶跃响应。
3 结论
1) 基于新的群智能优化算法,即教学与学习算法(TLBO)提出了一种新的自适应教学因子计算方法,经过函数测试,改进后的TLBO算法精度及稳定性上均优于原算法,达到了提高求解质量的预期目标。
2) 建立了刮板输送机伸缩机尾控制系统模型,并利用改进的TLBO算法进行PID参数整定,引入超调量指标对适应度函数进行完善,二次优化后的控制系统超调量明显改善,具备了良好控制品质和鲁棒性。
[1] 孟国营, 李国平, 沃磊, 等. 重型刮板输送机成套装备智能化关键技术[J]. 煤炭科学技术, 2014, 42(9): 57−60. MENG Guoying, LI Guoping, WO Lei, et al. Intellingent key technologies of complete heavy scraper conveyor equipment[J]. Coal Science and Technology, 2014, 42(9): 57−60.
[2] RAO R V, SAVSANI V, VAKHARIA D. Teaching-learning based optimization: A novel method for constrained mechanical design optimization problems[J]. Computer-Aided Design, 2011, 43(3): 303−315.
[3] RAO R V, SAVSANI V, VAKHARIA D. Teaching-learning- based optimization: an optimization method for continuous non-linear large scale problems[J]. Information Sciences, 2012, 183(1): 1−15.
[4] WANG Gaige, GANDOMI A H, YANG Xinshe, et al. A novel improved accelerated particle swarm optimization algorithm for global numerical optimization[J]. Engineering Computations, 2014, 33(7): 1198−1220.
[5] GHAMISI P, COUCEIRO M S, MARTINS F M L, et al. Multilevel image segmentation based on fractional-order darwinian particle swarm optimization[J]. Geoscience and Remote Sensing, 2014, 52(5): 2382−2394.
[6] OZTURK C, HANCER E, KARABOGA D. A novel binary artificial bee colony algorithm based on genetic operators[J]. Information Sciences, 2015, 297(10): 154−170.
[7] 于坤杰, 王昕, 王振雷. 改进的教学优化算法及其应用[J]. 化工进展, 2014, 33(4): 850−854. YU Kunjie, WANG Xin, WANG Zhenlei.Study and application of improved teaching-learning-based optimization algorithm[J].Chemical Industry and Engineering Progress, 2014, 33(4): 850−854.
[8] TAHER N, RASOUL A A, MOHAMMAD R N. A new multi objective optimization approach based on TLBO for location of automatic voltage regulators in distribution systems[J]. Engineering Applications of Artificial Intelligence, 2012, 25(8): 1577−1588.
[9] RAO R V, PATEL V. Multi-objective optimization of two stage thermoelectric cooler using a modified teaching–learning-based optimization algorithm[J]. Engineering Applications of Artificial Intelligence, 2013, 26(1): 430−445.
[10] 毛君, 张东升, 师建国. 刮板输送机张力自动控制系统的仿真研究[J]. 系统仿真学报, 2008, 20(16): 4474−4484. MAO Jun, ZHANG Dongsheng, SHI Jianguo. Simulation research of tension automatic control system of scraper conveyor[J]. Journal of System Simulation, 2008, 20(16): 4474−4484.
[11] 董立红, 赵鹏兵. 带式输送机拉紧装置张力的灰色预测PID控制[J]. 煤炭学报, 2013, 38(2): 342−347. DONG Lihong, ZHAO Pengbing. Grey predictive PID control of the tensioning device system in belt conveyor[J]. Journal of China Coal Society, 2013, 38(2): 342−347.
[12] 王文斌. 机械设计手册:液压传动与控制[M]. 北京: 机械工业出版社, 2007: 190−225. WANG Wenbin. Mechanical design handbook: pneumatic drive and control[M]. Beijing: China Machine Press, 2007: 190−225.
[13] 王晶. 基于PID 控制的带式输送机液压拉紧系统[J]. 辽宁工程技术大学学报(自然科学版), 2010, 29(S): 102−104. WANG Jing. Study on hydraulic tensioning system of belt conveyors based on PID control[J]. Journal of Liaoning Technical University (Natural Science), 2008, 20(16): 4474−4484.
[14] 刘道. 基于改进粒子群优化算法的PID参数整定研究[D]. 衡阳: 南华大学电气工程学院, 2012: 30−34. LIU Dao. Research on PID parameters tuning based on improved PSO algorithm[D]. Hengyang: University of South China. School of Electrical Engineering, 2012: 30−34.
[15] 拓守恒, 雍龙泉. 一种用于PID控制的教与学优化算法[J]. 智能系统学报, 2014, 9(6): 740−746. TOU Shouheng, YONG Longquan. A modified teaching- learning-based optimization algotithm for parameter tuning of a PID controller[J]. CAAI Transactions on Intelligent Systems, 2014, 9(6): 740−746.
(编辑 杨幼平)
Optimization of scraper conveyor extensible tail PID control system based on improved TLBO algorithm
HU Kun1, ZHANG Changjian1, WANG Shuang1, HAN Sheng2
(1. Key Laboratory of Safety and High Efficiency Mining of Ministry of Education, Anhui University of Science and Technology, Huainan 232001, China;2. Department of Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong 999077, China)
In order to improve the work performance of scraper conveyor extensible tail control system, a new swarm intelligence optimization algorithm, i.e. teaching learning based optimization (TLBO) algorithm was used to optimize the tail's PID controller parameters. And a new adaptive calculation method of teaching factor was proposed, making use of the variation of the marks obtained by the learners before and after a complete learning phase to determine the values of teaching factors. The results show that the precision and stability of improved TLBO algorithm are superior to those of standard TLBO. On the basis of the established model of scraper conveyor extensible tail control system, the PID controller parameters are tuned by the improved TLBO algorithm. Furthermore the overshoot volume control index is introduced to the fitness function to improve the PID optimization. The secondary optimized control system of scraper conveyor extensible tail has good control quality and robustness.
scraper conveyor; extensible tail; TLBO; teaching factor; PID parameters optimization
10.11817/j.issn.1672-7207.2017.01.015
TH222
A
1672−7207(2017)01−0106−06
2016−01−17;
2016−03−12
国家自然科学基金资助项目(51475001);中国博士后科学基金资助项目(2013M540506);安徽省博士后基金资助项目(2014B037) (Project(51475001) supported by the National Natural Science Foundation of China; Project(2013M540506) supported by China Postdoctoral Science Foundation; Project(2014B037) supported by the Postdoctoral Foundation of Anhui Province)
胡坤,博士,副教授,从事运输机械的研究;E-mail: hk924@126.com

