载波与接收机频差对时延差估算的影响及消除
张旭海,黄长江,华宇
载波与接收机频差对时延差估算的影响及消除
张旭海1,2,3,黄长江1,2,华宇1,2
(1. 中国科学院 国家授时中心,西安 710600;2. 中国科学院 精密导航定位与定时技术重点实验室,西安 710600;3. 中国科学院大学,北京 100049)
TDOA(到达时间差)算法通过测量信号到达若干组接收站的时间差,来确定信号源与接收站间的距离,从而确定信号源的位置。时延差估计是TDOA算法中重要的环节,信号的载波频率与接收设备的频率偏差都会对时延差估计精度造成影响。提出一种提高时延差估计精度的方法,并进行了仿真。仿真结果表明该方法消除了载波与频率偏差造成的影响,提高了时延差估计精度。
TDOA;互相关运算;载波;频偏
0 引言
在TDOA(到达时间差)测距算法中,时延差是进行测距的一个重要参数,估算时延差的一种主流方法是通过对接收信号进行互相关运算并根据相关峰值的位置估计时延差[1-2]。然而在实际应用中,由于接收设备的硬件设计误差,环境影响,或者是信号基带中心频率未知,导致载波信号解调后存在频偏与信号载波频率去除不完全等现象,这会严重改变相关峰的位置与波形进而影响估计精度[3]。本文就互相关运算中信号载波与频率偏差对相关结果造成影响的原因,做了研究与讨论,并提出了一种在无法彻底消除接收机频偏(下文中简称为频偏)与载波的情况下提高时延差估计精度的方法,该方法通过对接收信号进行数字二次变频,采用正交三角函数作为变频因子,之后对变频后的信号做平方和的方式,消除了载波与频偏对时延差估计造成的影响。
1 载波对相关函数的影响
射频无线电信号的发射流程通常为基带信号调制为中频信号,中频信号与本地振荡混频并滤波后产生射频信号并发射。在这一过程中,混频将信号从低频段搬移到了高频段,将信号调制于高频载波之上。
理论上,带载波的信号,其互相关函数可以由以下过程推导:

。 (2)
为了研究载波频率对相关函数具体产生怎样的影响,采用了仿真试验。试验中采用频率为4 kHz的标准余弦信号作为试验用载波信号,采用码速率为1.023 kHz的伪随机码作为试验用基带信号[4],且对其进行一定的延时作为互相关运算中的另一路信号。
1.1 余弦函数的相关结果

类似地,周期函数的相关函数也是周期函数[6],实验结果亦证明了这一点。图1为以上余弦函数的相关结果。
图1 余弦函数互相关结果
1.2 伪随机码的相关结果

图2所示的结果中,相关峰位置为20 000,幅度为19 105,相关峰三角形的宽度大约为150点宽度。相关结果出现了明显的相关峰,相邻处不存在任何其他副峰,顶部尖锐,底部平缓,属于非常典型的非周期信号相关波形。下文中其他结果均以图2为比较基准。
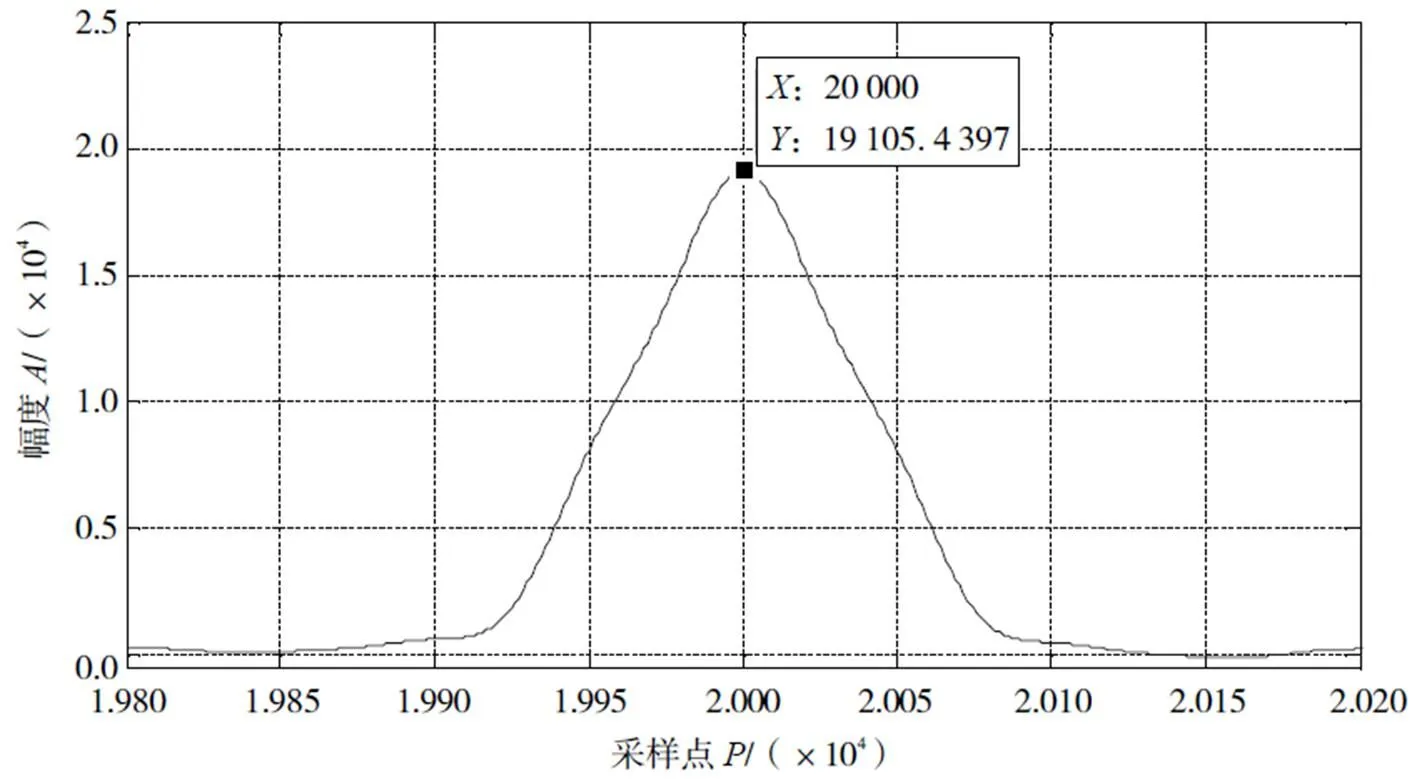
图2 伪随机码的互相关结果
1.3 频谱搬移至不同中频段的伪随机码的自相关结果
采用余弦信号与伪随机码相乘,将原始伪随机码的中频分别搬移至8 kHz,16 kHz并对频谱搬移后的信号做相关运算,图3显示了相应的相关结果。

(a) 8 kHz中频互相关结果
(b) 16 kHz中频互相关结果
图3 8 kHz,16 kHz中频伪随机码互相关结果
试验结果表明,处于非零中频的伪随机码的相关结果中,均出现了明显的相关峰。然而,两组不同中频的伪随机码的相关峰附近均存在逐渐衰减的副峰,且相关峰附近都产生了明显的正负振荡。另外,对8 kHz与16 kHz中频而言,其峰值位置均为20000,震荡幅度均约为19100,包络线宽度约为150点。因此,与零中频的伪随机码的相关结果相比,两种频段中频伪随机码的相关峰位置,峰值幅度,宽度与零中频伪随机码完全一致。
通过上述对比试验,可以假设,导致相关峰附近产生逐步衰减的振荡现象的原因是原始信号中存在一定的周期成分,整体的相关结果可以认为是信号中非周期成分的相关结果与周期成分的相关结果相互叠加而成。因此试验中中频越高的信号其相关峰的振荡频率越高,但其相关峰的位置,幅度等参数都完全一致,一致的参数保证了一致的时延差估算结果,故可以认为载波仅对相关波形有影响,对时延差估计没有影响。
2 频率偏差对相关函数的影响
通常,对接收到的射频信号需要做下变频处理变频至中频之后,才可用于后续处理,但由于接收设备中变频器在变频一致性上存在一定的误差,在下变频的过程中无法做到变频精度与变频值完全一致,导致信号产生频率差,这种频率差会对相关结果产生影响。下面通过数学表达式说明其影响。

, (6)


取前述采用的16 kHz中频伪随机码作为输入信号,分两路进行下变频,变频至4kHz中频,两路信号中某一路的下变频频率偏差分别设置为0.5,2,5 Hz。图4显示了这一试验过程。
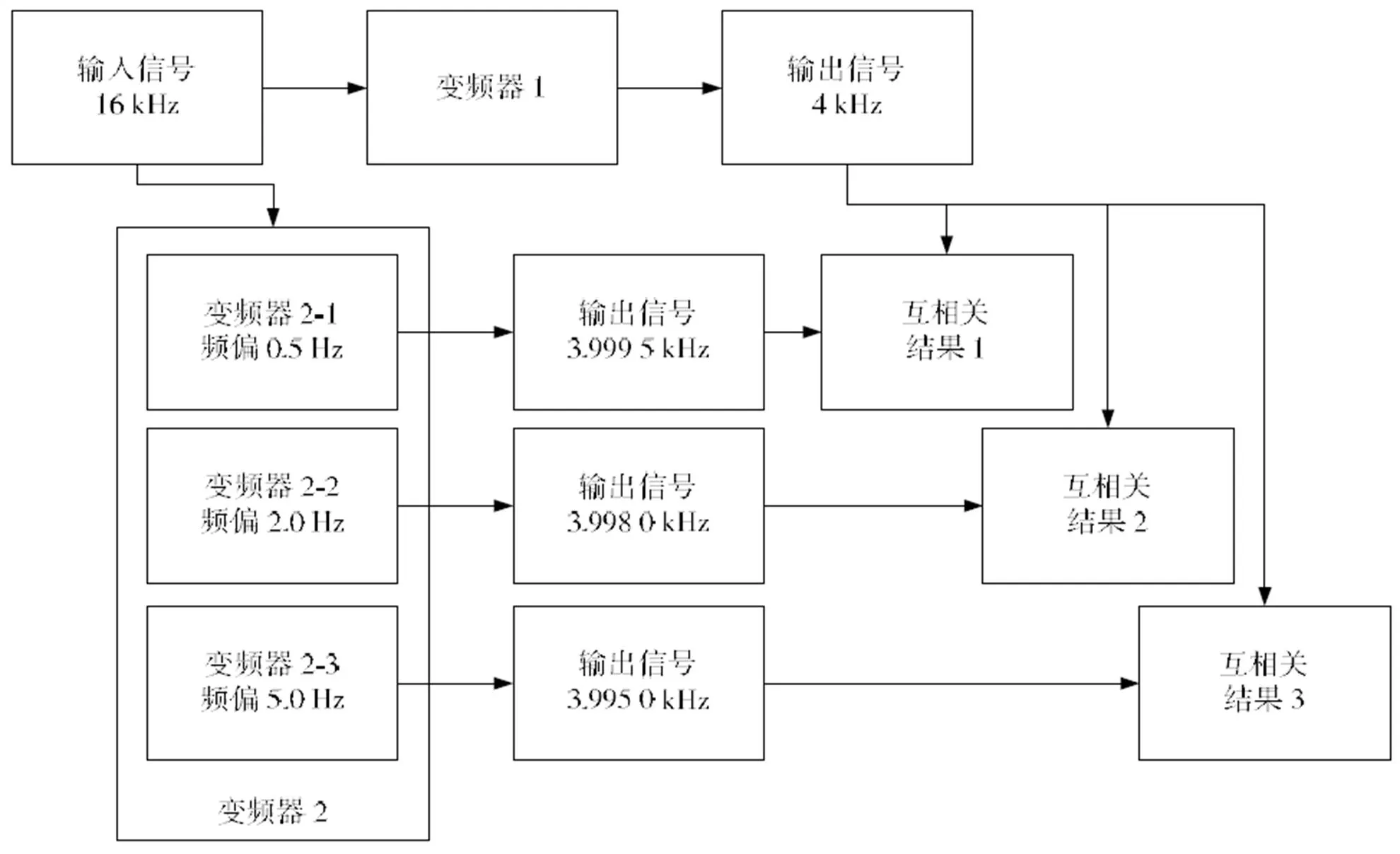
图4 频偏影响试验流程
之后对此两路输出信号进行互相关,对比结果,图5显示其相关结果。
(a) 0.5 Hz频偏互相关结果
(b) 2 Hz频偏互相关结果
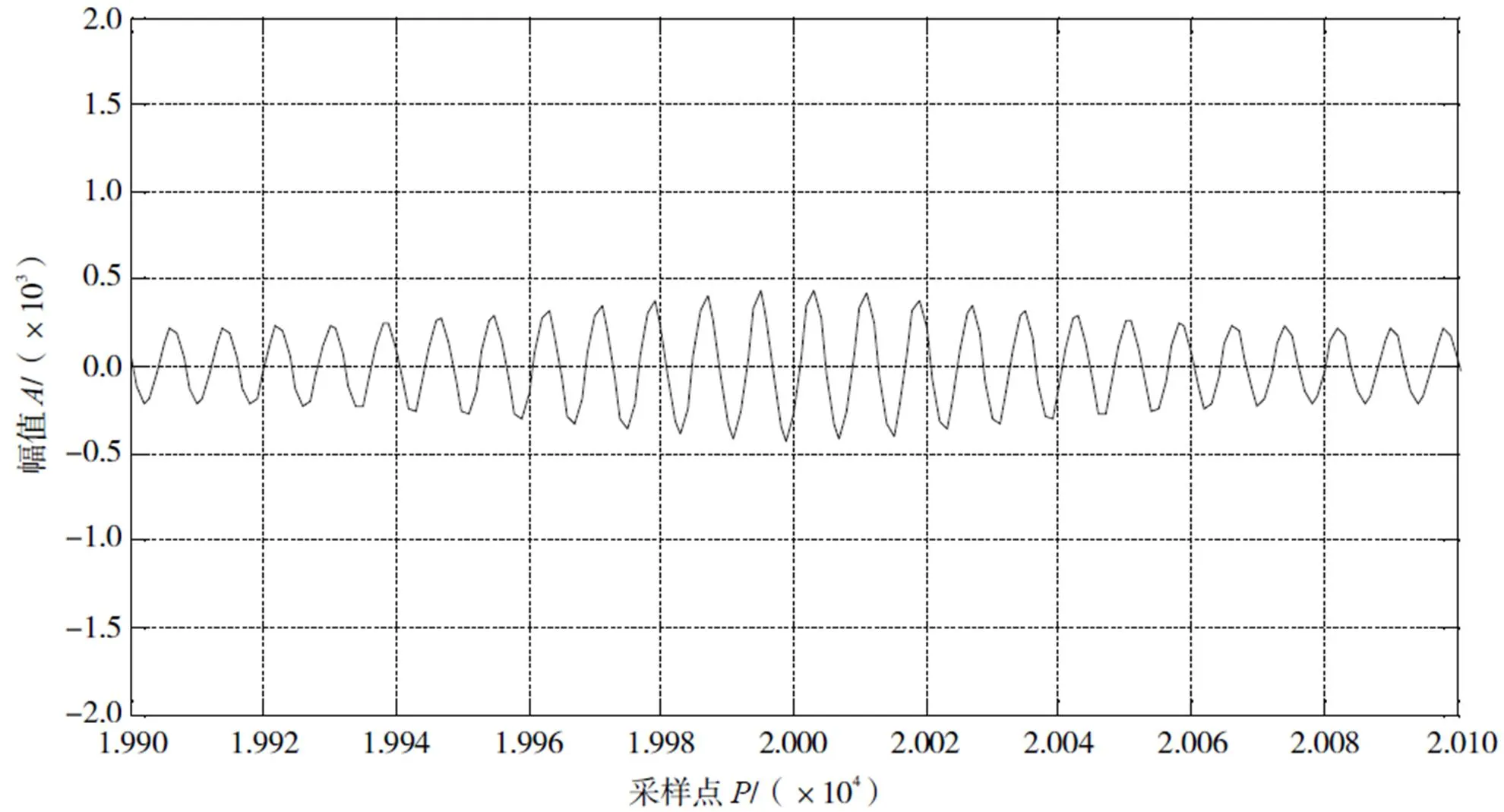
(c) 5 Hz频偏互相关结果(无法得到有效结果)
结果显示,0.5 Hz频偏的相关波形中峰值位置为20 001,下变频中信号通过低通滤波器幅度减半,去除滤波器影响后的峰值幅度约为8600,宽度150点,对比显示,峰值位置偏离1个点,峰值幅度减小,说明相关性下降,但宽度几乎没有变化;2 Hz频偏的相关波形中,峰值位置偏离至20 002,且由正峰变为负峰,去除滤波器影响后的峰值幅度约为3 000,宽度变为大约300点,可以看出2 Hz的频偏已经对相关波形造成了极大的影响:峰值偏离,幅度降低,宽度增加,表明相关性已经严重下降;5Hz的频率偏差已经导致无法得到相关峰,两路信号之间基本不具有相关性。相关峰位置的偏离会对时延差估算结果产生影响,实验中采样率为80kHz,仅一个采样点的变化,即可导致12.5μs的时间误差,因此频率偏差对相关结果与时延差估计的影响非常显著。
3 精度优化方法
根据前述结论,导致时延差估算精度变差的主要原因在于频率偏差,以下提出一种在采用互相关法进行时延差估算中消除频偏误差,提高精度的方法。
频率偏差主要产生在变频过程中,受制于设备精度,难以完全消除;残留载波则会导致相关函数产生振荡。对于以上两种问题,可以通过对信号进行数字二次变频并采用正交三角函数的方法彻底消除频偏与载波,以下流程图(图6)简要说明了处理过程,以下公式说明了具体推导过程。
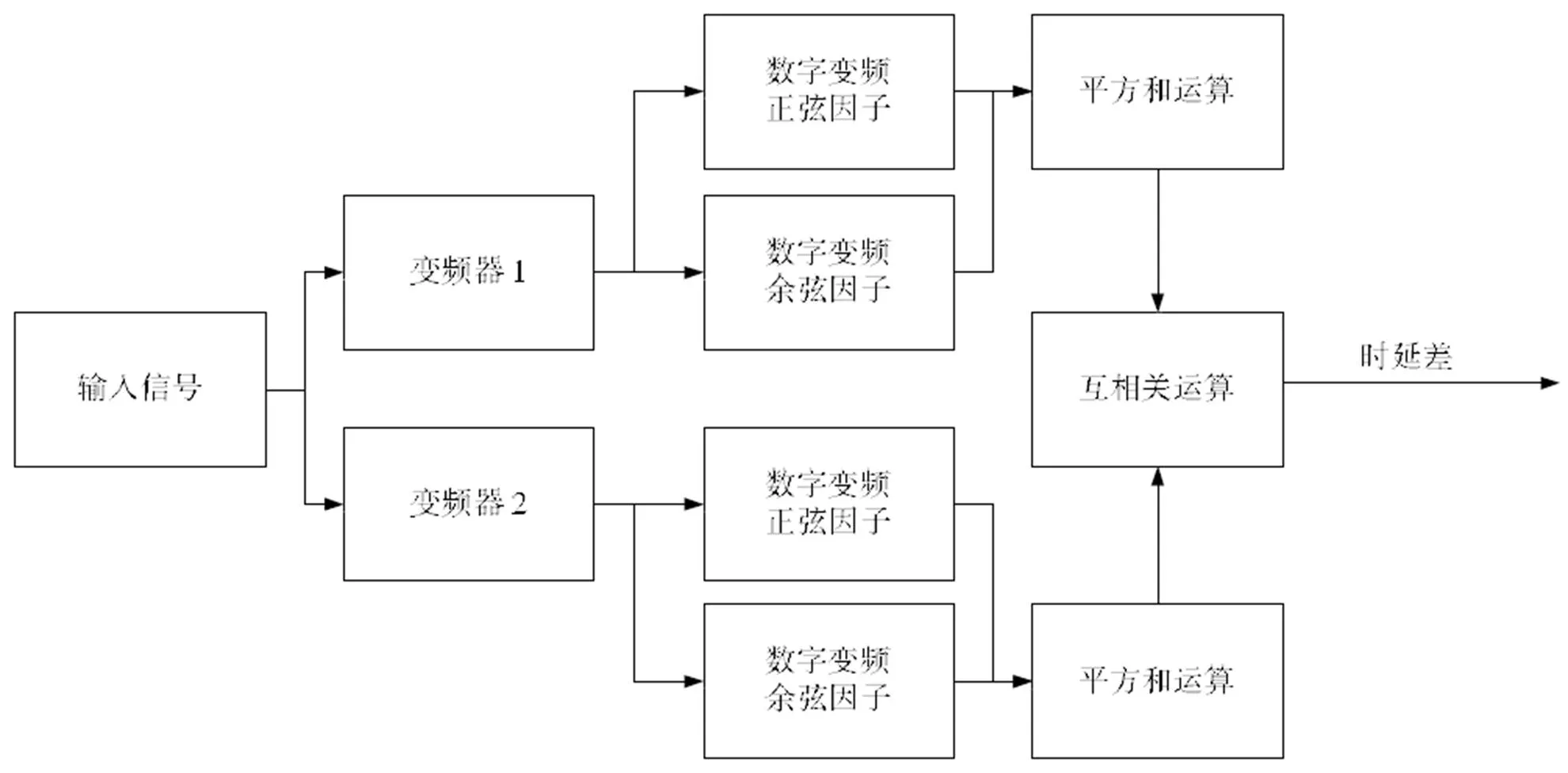
图6 数字二次变频消除频偏与载波流程
接收到的信号仍然采用上述的
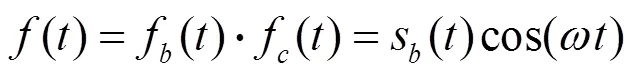
通过两路相同指标的变频器,可得:
第一路:

经过低通滤波后可以得到
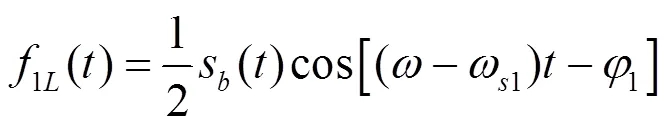
第二路:
, (12)
经过低通滤波后可以得到

, (14)
经过低通滤波后可以得到

, (16)
经过低通滤波后可以得到

将两路相互正交的二次变频输出信号求平方和,最终得到
。 (18)

经过低通滤波后可以得到
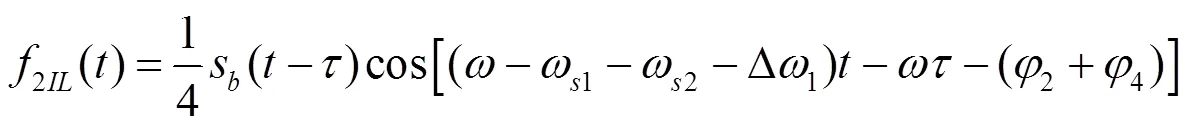
, (21)
经过低通滤波后可以得到
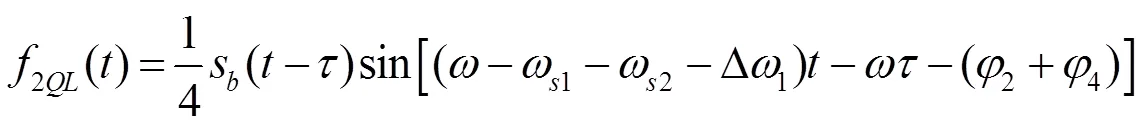
将两路相互正交的二次变频输出信号求平方和,最终得到
。 (23)
可以看出,经过采用两种变频因子进行二次变频并求平方和后,彻底消除了频率偏移与载波频率。通常,对信号直接进行平方和运算,可能会破坏信号所携带的信息,然而,平方和运算不会影响信号之间的时延差信息,故通过以上方法,能够在保留时延差的同时,消除载波与频偏造成的影响。
仍采用前文提到的16 Hz的中频伪随机码测试信号,令一次变频存在2Hz的频差,使用二次变频后最终结果由图7显示,显然,频偏与载波产生的影响已经完全消除。在一次变频频差为0.5Hz与5Hz的情况下,也得到了完全相同的结果。
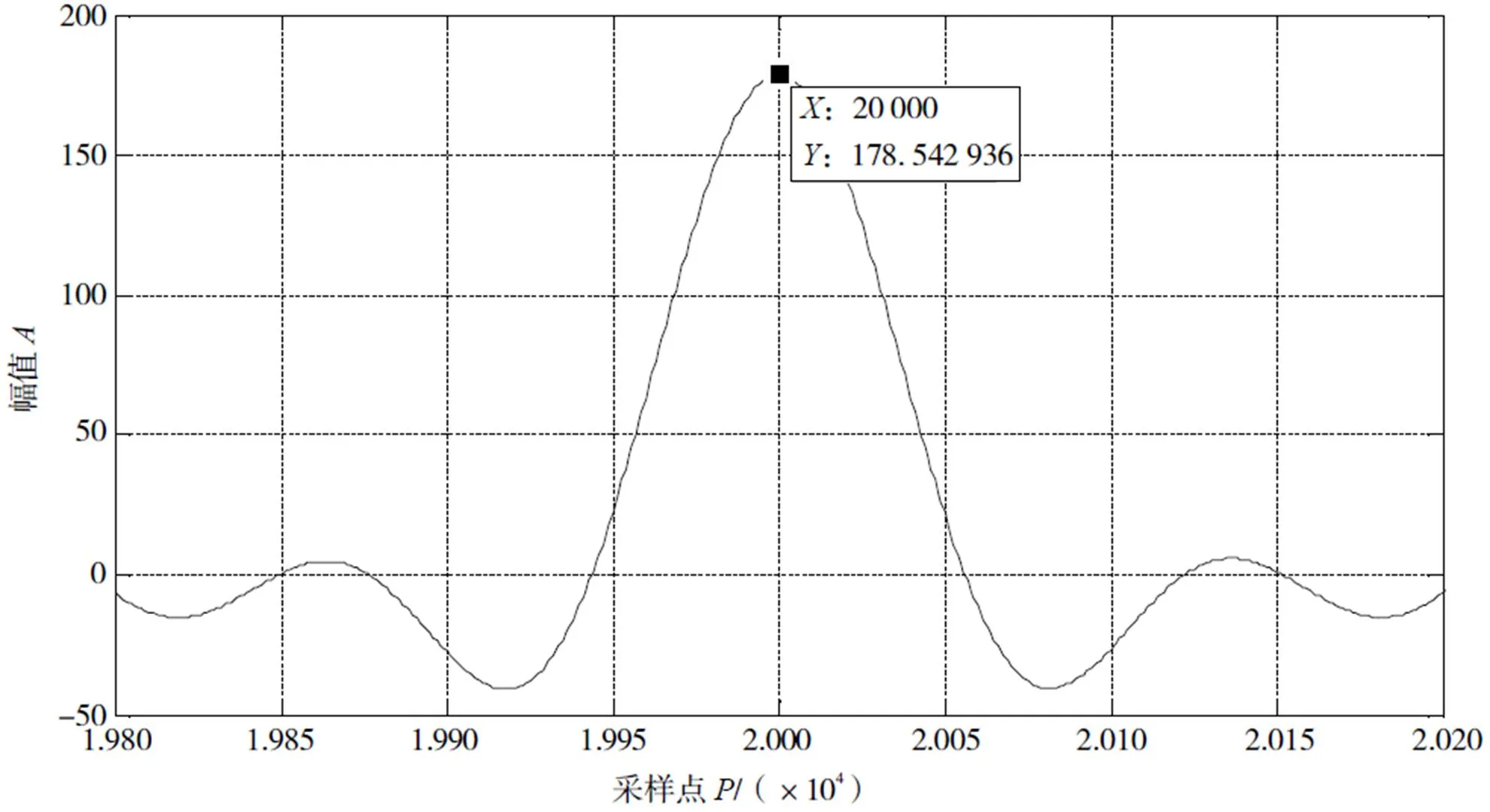
图7 经过优化后的伪随机码互相关结果
4 结语
本文通过分析实验,讨论了在TDOA算法中信号载波与接收机频差对时延差与相关函数的影响,并提出了一种消除载波与频差影响的方法,通过仿真实验表明该方法能够消除载波与频差,并改善时延差的估计精度。
[1] KNAPP C H, CARTER G C. The generalized correlation method for estimation of time delay[J].IEEE Transactions on Acoustics, Speech and Signal Processing, 1976, 24(4): 320-327.
[2] 梁宇, 马良, 纳霞, 等. 基于广义互相关算法的时延估计[J]. 计算机科学, 2011, 38(10A): 454-456.
[3] 史小红. 基于TDOA的无线定位方法及其性能分析[J]. 东南大学学报: 自然科学版, 2013, 43(2): 252-257.
[4] 谢伟, 蔡德林, 孙开荣, 等.GPS中伪随机码生成原理的研究[J]. 信息技术, 2007, 5: 113-116, 119.
[5] 王俊刚, 杨号. 基于互相关的正弦信号特征提取方法[J]. 海军航空工程学院学报, 2009, 24(3): 277-279, 288.
[6] 葛新成, 罗大成, 曹勇. 相关函数在数字信号处理中的应用[J]. 电光与控制, 2006, 13(6): 78-80, 85.
[7] 卢晓春, 陈清刚, 胡永辉.卫星导航定位系统中伪随机码的研究[J]. 时间频率学报, 2004, 27(1): 23-32.
Influence of carrier and receiver frequency deviation on time delay difference estimation and its elimination
ZHANG Xu-hai1,2,3, HUANG Chang-jiang1,2, HUA Yu1,2
(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;2. Key Laboratory of Precision Navigation and Timing Technology, National Time Service Center,Chinese Academy of Sciences, Xi’an 710600, China;3. University of Chinese Academy of Sciences, Beijing 100049, China)
TDOA (time difference of arrival) algorithm measures the distances between signal source and receive stations by measuring the time differences of arrival of signal to a number of receive stations, thusdetermines the signal source position. Time delay difference estimation is an important section in TDOA algorithm, however,the carrier and frequency deviation may influence the precision of the estimation. A method to improve the precision of time delay difference estimation is proposed in this paper, and the simulation results show that the method can eliminate the influence of carrier and frequency deviation and can improve the precision of time delay difference estimation.
TDOA; cross-correlation operation;carrier; frequency deviation
TN911.7
A
1674-0637(2017)01-0043-10
10.13875/j.issn.1674-0637.2017-01-0043-10
2016-05-18
国家自然科学基金青年基金资助项目(11403033)
张旭海,男,硕士,主要从事移动台室内定位技术研究。

