用于PWM滤波的频变电感研究
谷雨帅,赵治华,高雪平
用于PWM滤波的频变电感研究
谷雨帅,赵治华,高雪平
(海军工程大学,武汉 430033)
逆变器等输出的PWM波在经过滤波电感进行滤波后会得到所需的正弦波,但滤波电感在滤除开关器件产生的开关频率及其高次谐波的同时,也会对基波信号产生一定的衰减。滤波电感选择的难点在于滤波效果和电感基波压降无法同时达到最佳。针对这种问题,构建一种频变电感,其对高频谐波呈现高电感值(较高的感抗),而对基波呈现低电感值(比常规电感更低的感抗),通过磁通补偿方式实现高频滤波效果和低频基波压降均达到最佳。最后,通过仿真,对比分析了频变电感和传统滤波电感的滤波效果,验证了频变电感方案的可行性。
PWM波 磁通补偿 频变电感 滤波器
0 引言
电力电子技术的发展使得采用脉冲宽度调制(PWM)方式的逆变器得到了广泛的应用,如变频器、不间断电源(UPS)等。采用高速半导体开关器件,如IGBT、MOSFET等,可以大大加快逆变器的动态响应过程。然而,这些半导体开关产生的脉冲信号具有较大的v/t和di/dt,形成很强的高频谐波[1]。以电压型单相全桥逆变电路为例,若直流母线电压为1 V、调制比为0.8、基波频率50 Hz、载波频率即开关频率为1 kHz,则形成的PWM波的频谱如图1所示;其中, 基波频率为50 Hz,PWM的等效开关频率为2 kHz。
针对PWM波的等效开关频率及其高次谐波,常见的滤波形式主要有两种:第一种是通过串联大电感来减小高频谐波,但滤波电感量的增加将影响系统的动态性能且基波输出电压严重降低。第二种是通过采用三阶LCL滤波器代替原有的单电感滤波器,来解决上述问题[2],如图2。
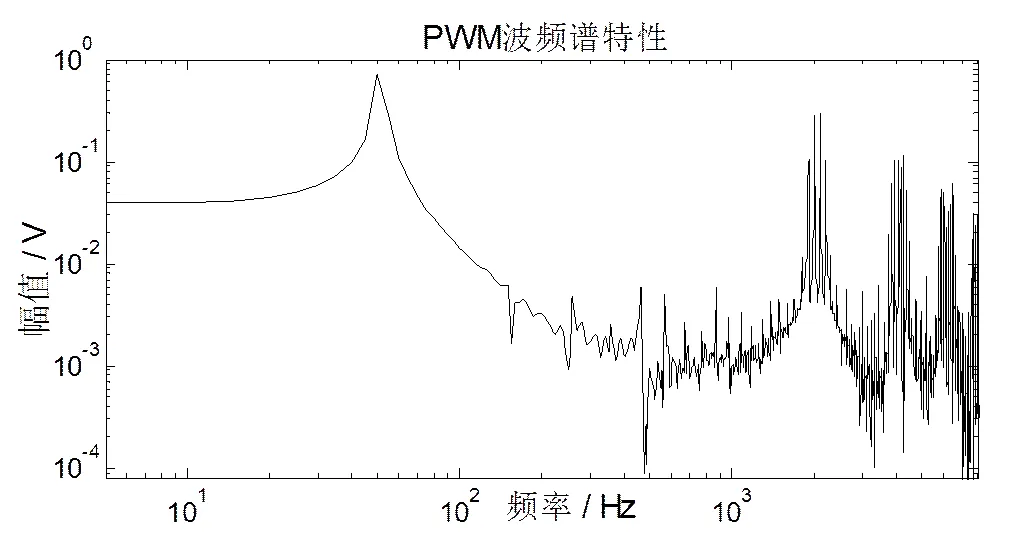
图1 PWM波频谱特性
图2 两种滤波电路原理图
LCL滤波器的电容的容抗值与电流频率成反比的特点来滤除高频谐波[3]。然而,滤波电容的分流作用,使变流器的电流控制系统由一阶变为三阶,控制更为复杂,并且在某些高次谐波电流下,LCL滤波器的总阻抗接近零,将导致谐振效应,影响系统的稳态性能。
以上两种滤波方式,无论是电感滤波器还是LCL滤波器都无法解决高次谐波与动态性能、以及输出电压的矛盾问题。本文设计一种频变电感,在进行滤波时,新型电感对高频谐波呈现高电感值(较高的感抗),达到滤除高频谐波的目的;而对基波呈现较小的电感值,比常规电感具有更低的感抗,以实现降低滤波电感上基波压降的目的;并通过分析和仿真验证了方法的可行性。
1 频变电感的原理与设计
1.1 频变电感的原理
对于负载电阻为L,采用常规滤波电感的电路(如图(2)中的单电感滤波电路)滤波特性为
式中,V为PWM电源输出电压,V为负载上电压。
而所需要的理想滤波特性为:

式中,ω为滤波电路的截止频率。
比较式(1)和(2)可以得到,需要的理想滤波电感应该具有“频变”特性

对于式(3)中理想滤波电感的“频变”特性,可以用下式近似逼近(k>1)
(4)
并且,可以进一步采用阶低通滤波电路
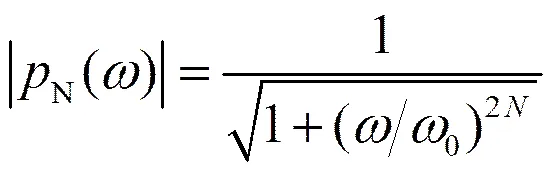
来近似实现“频变电感”
(6)
式中,分子和分母中函数均为N低通滤波函数,且截止频率满足

例如,对于图1所示的PWM波,低频基波频率ƒS=50 Hz,PWM等效开关频率ƒk=2 kHz,可以取频变电感的截止频率为
(8)
若选择=4,并选择二阶低通滤波函数,则两个低通滤波函数的截止频率为

而二阶低通滤波函数的形式为
(10)
图3所示为二阶频变电感的电感值随频率的变化特性,其中:=48 mH,=4,=2。可以看出,采用式(6)形式的频变电感,在1 kHz以上的高频段等效电感为48 mH,而100 Hz以下低频段的等效电感为12 mH,是式(3)理想滤波电感的一种近似实现方式。
1.2 频变电感的实现
图4为式(6)频变电感的一种实现方式,图中频变电感由信号提取、低通滤波、幅相调节、补偿绕组和滤波绕组等五个部分组成。通过信号提取获得主电路的电流I1,结果低通滤波和幅相调节,控制补偿绕组中电流I2,使滤波绕组对主电路呈现频变电感特性;核心部分为低通滤波和幅相调节。

图3 频变电感Le的频率特性

图4 频变电感结构原理示意图
1.2.1 低通滤波电路
以二阶频变电感为例,其低通滤波器可以采用图(5)电路实现。取R2=R1,C2=C1,且ωbR1C1=1,则其传递函数为

1.2.2 幅相调节电路
假设图4的频变电感电路中,PWM电源电压为VS,负载电阻为RL,补偿绕和滤波绕组的电感值均为L且互感M=L。根据电路原理,有
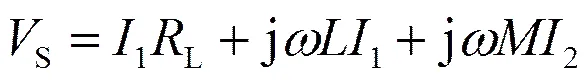
(13)
因此,要求

对于二阶频变电感,有ωa2=ωb2/k,可得
(15)
可见,在经过式(11)的低通滤波后,对于二阶频变电感需要的幅相调节为比例和微分变换,可用图6电路实现。取k=4,有

1.2.3 频变电感的控制电路
根上述设计,二阶频变电感的滤波电路,可用图7实现,滤波绕组和补偿绕组采用在一个磁环上平行绕制相同匝数的铜线得到。
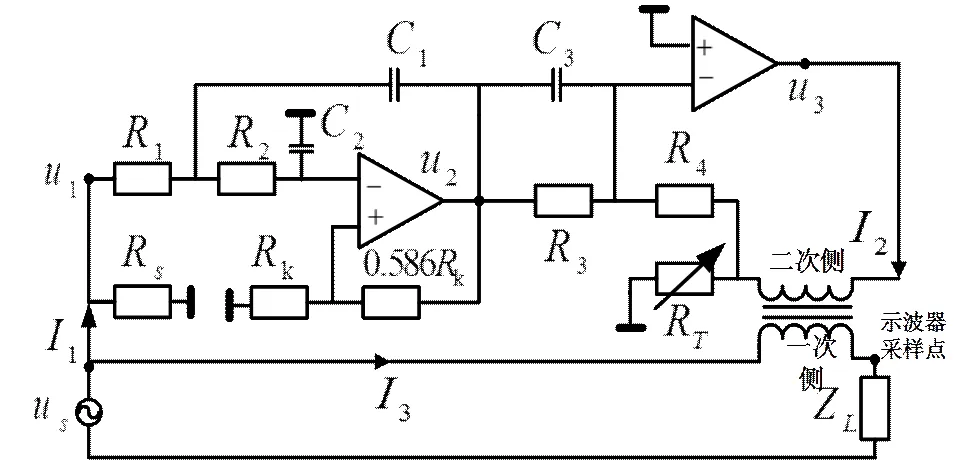
图7 频变电感电路图
在图7电路中:首先,通过电流传感器提取负载电流1并转换为电压1;然后,经过2阶低通滤波电路获得电压2;再,经过幅相调节电路获得电压3;最后,通过采样电阻T将输出电压3转换为补偿绕组电流2。
2 仿真验证
为验证依据磁通补偿原理构建的频变电感的可行性,按照图(7)所示电路构建仿真电路进行验证。1)PWM电源采用电压型单相全桥逆变电路,直流输入电压为1 V、调制比为0.8、载波频率即开关频率为1kHz(谐波频率为2 kHz);2)频变电感的滤波绕组和补偿绕组电感值均为48 mH,耦合系数约为0.99;3)负载为L=15 Ω的纯电阻;4)二阶低通滤波电路,,k=5kΩ,,根据以上参数,可得二阶低通滤波电路的截止频率为448 Hz;5)幅相调节电路,3=2.22 kΩ,4=1.05 kΩ,3=0.15 μF。
2.关税。为提高农业生产能力,降低农民生产负担,我国对化肥进口关税给予了相当大的优惠;化肥关税政策的大体方向为鼓励进口、限制出口。1997年始,国家对化肥关税政策实行配额内外有别的关税税率。1997~2002年我国对尿素和磷酸二铵的进口实行配额许可证限制;2002年以后,我国对全部化肥实行配额管理。为缓解化肥供需矛盾,针对不同化肥品种,不同年份会有不同的化肥进口优惠政策,实际执行的关税税率一度低至1%。
仿真时,示波器对波形其中一个周期进行采样。图8为PWM电源输出电压和频变电感滤波后负载电压的比较;图9和图10分别为采用48 mH和12 mH单电感滤波时,PWM电源输出电压和电感滤波后负载电压的比较。

图9 频变电感和12 mH单电感滤波效果图
比较图8和图9,可以看出:频变电感滤波时,负载电压基波幅值明显高于48 mH单电感滤波。频变电感输出幅值为0.787V、相位滞后角为14.1°,48 mH单电感输出幅值为0.612V、相位滞后45°,功率因数由0.71提高至0.97。
图10为图8、9的负载电压波形的频谱图,可以看到:频变电感的低频基波压降与12 mH电感相当,而高频滤波特性与48 mH电感相当。说明通过频变电感滤波后,实现了抑制高频谐波和减小基波压降的效果。
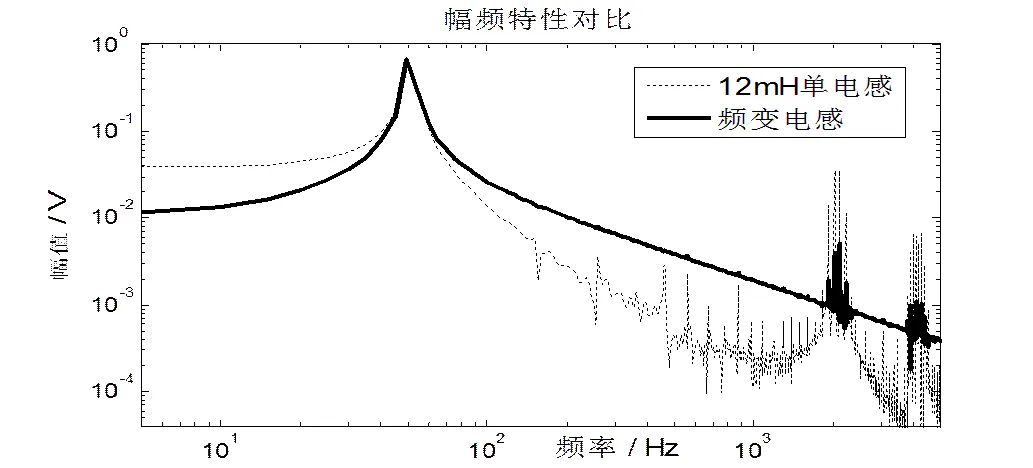
图10 频变电感和12 mH单电感幅频特性对比
频变电感滤波器的仿真结果,可以看出在基波衰减和谐波滤除方面明显优于传统单电感滤波效果,可以较完美第实现PWM波正弦化!
3 结论
此处研究了一种基于磁通补偿方式的频变电感,给出了其控制原理和实现形式。建立了应用此频变电感进行PWM滤波的结构框图,同时,给出了此频变电感的电路图,并且获得补偿电流幅值和相位的调节方法,给出了完整的控制模型。搭建了仿真实验平台,通过仿真验证了基于磁通补偿的频变电感用于PWM滤波的可行性。频变电感与12 mH和48 mH单电感滤波的对比,凸显了频变电感的滤波效果。
[1] 裴雪军.PWM逆变器传导电磁干扰的研究[D].武汉:华中科技大学,2004.
[2] Lindgren M,Svensson J. Connecting fast switching voltage-source converters to the grid-harmonic distortion and its reduction[C].IEEE Strock PowerTech Conference,Stockholm,1995:191-195.
[3] Marco Liserre, Frede Blaabjerg, Remus Teodorescu. Grid impedance detection via excitation of LCL-filter resonance[C]. Applications Conference,2005Fourtieth IAS Annual Meeting. Kowloon, HongKong, China, 2005,(2): 910-916.
Study on Frequency-dependent Inductance Used in PWM Filtering
Gu Yushuai, Zhao Zhihua, Gao Xueping
(Naval University of Engineering, Wuhan 430033,China)
TM463
A
1003-4862(2017)03-0001-04
2016-09-15
国家自然科学基金(61201055),(51422705)
谷雨帅(1991-),男,硕士。研究方向:电力系统电磁兼容。

